7.3: Teoría de Campo Media

Template:MathJaxArovas

Consideremos el modelo de Ising Hamiltoniano,

\[\HH=-J\sum_{\langle ij\rangle} \sigma_i\,\sigma_j -H\sum_i \sigma_i\ ,\]

donde la primera suma en el RHS está sobre todos los enlaces de la celosía. Cada giro puede ser 'up' (\(\sigma=+1\)) o 'down' (\(\sigma=-1\)). Asumimos además que los giros están ubicados en una celosía de Bravais ⁸ y que el acoplamiento\(J_{ij}=J\big( |\BR_i - \BR_j|\big)\), donde\(\BR_i\) está la posición del\(i^{\ssr{th}}\) giro.

En cada sitio\(i\) nos descomponemos\(\sigma\ns_i\) en una contribución de su promedio termodinámico y un término de fluctuación,

\[\sigma\ns_i=\langle\sigma\ns_i\rangle + \delta\sigma\ns_i\ .\]

Escribiremos\(\langle\sigma\ns_i\rangle\equiv m\), la magnetización local (adimensional), y asumiremos que\(m\) es independiente de la posición\(i\). Entonces

\[\begin{split} \sigma\ns_i\,\sigma\ns_j &= (m+\delta\sigma\ns_i)\,(m+\delta\sigma\ns_j)\\ &=m^2 + m\,(\delta\sigma\ns_i + \delta\sigma\ns_j) + \delta\sigma\ns_i\,\delta\sigma\ns_j\\ &=-m^2 + m\,(\sigma\ns_i + \sigma\ns_j) + \delta\sigma\ns_i\,\delta\sigma\ns_j\ . \end{split}\]

El último término sobre el RHS de la segunda ecuación anterior es cuadrático en las fluctuaciones, y asumimos que esto es insignificante. Así, obtenemos el campo medio hamiltoniano

\[\HH\ns_{\ssr{MF}}=\half NzJ\,m^2- \big(H+zJm\big)\sum_i\sigma_i\ ,\]

donde\(N\) es el número total de sitios de celosía. El primer término es una constante, aunque aún no\(m\) se ha determinado el valor de. Los pesos Boltzmann están entonces completamente determinados por el segundo término, que es justo lo que escribiríamos para un hamiltoniano de giros no interactuantes en un 'campo medio' efectivo

\[H\ns_{eff}=H+zJm\ .\]

En otras palabras,\(H\ns_{eff}=H\ns_{ext} + H\ns_{int}\), donde se aplica el campo externo\(H\ns_{ext}=H\), y el 'campo interno' es\(H\ns_{int}=zJm\). El campo interno da cuenta de la interacción con los valores promedio de todos los demás giros acoplados a un giro en un sitio dado, de ahí que a menudo se le llama el 'campo medio'. Dado que los giros no interactúan, tenemos

\[m={e^{\beta H\ns_{eff}} - e^{-\beta H\ns_{eff}} \over e^{\beta H\ns_{eff}} + e^{-\beta H\ns_{eff}} } =\tanh\!\bigg({H+zJm\over\kT}\bigg)\ .\]

Es un asunto sencillo de resolver por la energía libre, dada la hamiltoniana que no interactúa\(\HH\ns_{\ssr{MF}}\). La función de partición es

\[Z=\Tra e^{-\beta\HH\ns_{\ssr{MF}}}=e^{-\half \beta NzJ\,m^2} \bigg(\sum_\sigma e^{\beta (H+zJm)\sigma}\bigg)^{\!N} =e^{-\beta F}\ .\]

Ahora definimos variables adimensionales:

\[f\equiv {F\over NzJ}\qquad,\qquad\theta\equiv {\kT\over zJ}\qquad,\qquad h\equiv {H\over zJ}\ ,\]

y obtener la energía libre adimensional

\[f(m,h,\theta)=\half m^2 - \theta\,\ln \bigg(e^{(m+h)/\theta} + e^{-(m+h)/\theta}\bigg)\ . \label{fergsca}\]

Diferenciando con respecto a\(m\) da la ecuación media del campo,

\[m=\tanh\Big({m+h\over \theta}\Big)\ , \label{isingmft}\]

lo que equivale al requisito de autoconsistencia,\(m=\langle \sigma_i\rangle\).

\(h=0\)

Cuando\(h=0\) la ecuación del campo medio se convierte

\[m=\tanh\Big({m\over \theta}\Big)\ .\]

Esta ecuación no lineal se puede resolver gráficamente, como en el panel superior de la Figura\ ref {IMFZh}. El RHS en una función tanh que se empina con la disminución\(t\). Si, at\(m=0\), la pendiente de\(\tanh(m/\theta)\) es menor que la unidad, entonces la curva\(y=\tanh(m/h)\) se cruzará\(y=m\) solo en\(m=0\). No obstante, si la pendiente es mayor que la unidad, habrá tres de esas intersecciones. Dado que la pendiente es\(1/\theta\), identificamos\(\theta\ns_\Rc=1\) como la temperatura media de transición de campo.

Figura\(\PageIndex{1}\): Results for \(h=0\). Paneles superiores: solución gráfica a la ecuación de autoconsistencia\(m=\tanh(m/\theta)\) at temperatures \(\theta=0.65\) (blue) and \(\theta=1.5\) (dark red). Lower panel: mean field free energy, with energy shifted by \(\theta\ln 2\) so that \(f(m=0,\theta)=0\).

En la fase de baja temperatura\(\theta<1\), hay tres soluciones a las ecuaciones de campo promedio. Una solución está siempre en\(m=0\). Las otras dos soluciones deben estar relacionadas por la\(m\leftrightarrow -m\) simetría de la energía libre (cuando\(h=0\)). Las energías libres exactas se trazan en el panel inferior de la Figura\(\PageIndex{1}\), pero es posible hacer progresos analíticos asumiendo que\(m\) es pequeña y Taylor expandiendo la energía libre\(f(m,\theta)\) en potencias de\(m\):

\[\begin{split} f(m,\theta)&=\half m^2 -\theta\ln2 -\theta\,\ln\cosh\Big({m\over \theta}\Big)\\ &=-\theta\,\ln 2 + \half\,(1-\theta^{-1})\,m^2 +{m^4\over 12\,\theta^3} - {m^6\over 45\,\theta^5} + \ldots\ . \end{split}\]

Obsérvese que el signo del término cuadrático es positivo para\(\theta>1\) y negativo para\(\theta<1\). Así, la forma de la energía\(f(m,\theta)\) libre en función de los cambios\(m\) cualitativos en este punto\(\theta\ns_\Rc=1\), la temperatura media de transición del campo, también conocida como la temperatura crítica.

Para\(\theta>\theta\ns_\Rc\), la energía libre\(f(m,\theta)\) tiene un solo mínimo en\(m=0\). Abajo\(\theta\ns_\Rc\), la curvatura en\(m=0\) reversa, y\(m=0\) se convierte en un máximo local. Luego hay dos mínimos equivalentes desplazados simétricamente a cada lado de\(m=0\). Diferenciando con respecto a\(m\), encontramos estos mínimos locales. Para\(\theta<\theta\ns_\Rc\), los mínimos locales se encuentran en

\[m^2=3\theta^2(1-\theta) = 3 (1-\theta) + \CO\big((1-\theta)^2\big)\ .\]

Así, encontramos para\(|\theta-1|\ll 1\),

\[m(\theta,h=0)=\pm\sqrt{3}\,\big(1-\theta\big)_+^{1/2}\ ,\]

donde el\(+\) subíndice indica que esta solución es sólo para\(1-\theta>0\). Porque\(\theta>1\) la única solución es\(m=0\). El exponente con el que se\(m(\theta)\) desvanece como\(\theta\to \theta^-_\Rc\) se denota\(\beta\). \(m(\theta,h=0) \propto(\theta\ns_\Rc-\theta)_+^\beta\).

Calor específico

Ahora podemos expandir la energía libre\(f(\theta,h=0)\). ENCONTRAMOS

\[f(\theta,h=0)=\begin{cases} -\theta\ln 2 & \hbox{if $\theta>\theta\ns_\Rc$}\\ -\theta\ln 2-{3\over 4} (1-\theta)^2 + \CO\big( (1-\theta)^4\big) & \hbox{if $\theta<\theta\ns_\Rc$}\ . \end{cases}\]

Así, si calculamos la capacidad calorífica, nos encontramos en las proximidades de\(\theta=\theta\ns_\Rc\)

\[c\ns_V=-\theta\,{\pz^2\!f\over\pz \theta^2}=\begin{cases} 0 & \hbox{if $\theta>\theta\ns_\Rc$}\\ {3\over 2} & \hbox{if $\theta<\theta\ns_\Rc$}\ . \end{cases}\]

Así, el calor específico es discontinuo en\(\theta=\theta\ns_\Rc\). Destacamos que esto sólo es válido cerca\(\theta=\theta\ns_\Rc=1\). El resultado general válido para todos\(\theta\) es ⁹

\[c\ns_V(\theta)={1\over \theta}\cdot{m^2(\theta)-m^4(\theta)\over \theta-1+m^2(\theta)}\ ,\]

Con esta expresión se pueden comprobar ambos límites\(\theta\to 0\) y\(\theta\to \theta\ns_\Rc\). Como\(\theta\to 0\) la magnetización se satura y uno tiene\(m^2(\theta) \simeq 1-4\,e^{-2/\theta}\). El numerador entonces se desvanece como\(e^{-2/\theta}\), lo que abruma el denominador que a su vez se desvanece como\(\theta^2\). En consecuencia,\(c\ns_V(\theta\to 0) =0\), como se esperaba. Como\(\theta\to 1\), invocando\(m^2\simeq 3(1-\theta)\) nos recuperamos\(c\ns_V(\theta_\Rc^-)=\frac{3}{2}\).

En la teoría de los fenómenos críticos,\(c\ns_V(\theta)\propto |\theta-\theta\ns_\Rc|^{-\alpha}\) como\(\theta\to \theta\ns_\Rc\). Vemos que la teoría de campo media rinde\(\alpha=0\).

Figura\(\PageIndex{2}\): Resultados para\(h=0.1\). Paneles superiores: solución gráfica a la ecuación de autoconsistencia\(m=\tanh\!\big((m+h)/\theta\big)\) a temperaturas\(\theta=0.65\) (azul),\(\theta=0.9\) (verde oscuro) y\(\theta=1.5\) (rojo oscuro). Panel inferior: energía media libre de campo, con energía desplazada por\(\theta\ln 2\) para que\(f(m=0,\theta)=0\).

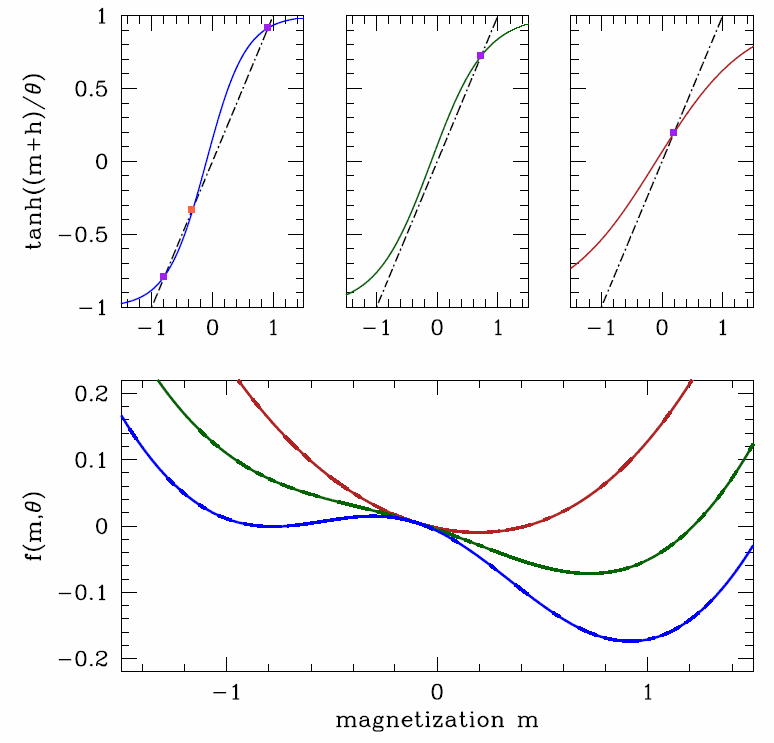
\(h\ne 0\)

Considerar sin pérdida de generalidad el caso\(h>0\). El mínimo de la energía libre\(f(m,h,\theta)\) ahora se encuentra en\(m>0\) para cualquiera\(\theta\). A bajas temperaturas, la estructura de pozo doble que encontramos en el\(h=0\) caso se inclina para que el pozo derecho quede más bajo en energía que el pozo izquierdo. Esto se representa en la Figura\(\PageIndex{2}\). A medida que se eleva la temperatura, el mínimo local a\(m<0\) desaparece, aniquilando con el máximo local en una bifurcación de nodo silla de montar. Para encontrar dónde sucede esto, uno establece\({\pz f\over\pz m}=0\) y\({\pz^2\!f\over\pz m^2}=0\) simultáneamente, dando como resultado

\[h^*(\theta)=\sqrt{1-\theta}-{\theta\over 2}\ln\!\bigg({1+\sqrt{1-\theta}\over 1-\sqrt{1-\theta}}\bigg) . \label{IMFhstar}\]

Las soluciones se encuentran en\(h=\pm h^*(\theta)\). Para\(\theta<\theta\ns_\Rc=1\) y\(h\in \big[\!-\!h^*(\theta)\,,\,+h^*(\theta)\big]\), hay tres soluciones a la ecuación de campo medio. Equivalentemente podríamos en principio invertir la expresión anterior para obtener\(\theta^*(h)\). Porque\(\theta>\theta^*(h)\), solo hay un mínimo global único en la energía libre\(f(m)\) y no hay mínimo local. Nota\(\theta^*(h=0)=1\).

Asumiendo\(h\ll |\theta-1|\ll 1\), la solución de campo medio para también\(m(\theta,h)\) será pequeña, y expandimos la energía libre en\(m\), y al orden lineal en\(h\):

\[\begin{split} f(m,h,\theta)&=-\theta\,\ln 2 + \half (1-\theta^{-1})\, m^2 + {m^4\over 12\, \theta^3} - {hm\over \theta}\\ &=f\nd_0 + \half\, (\theta-1)\,m^2 + \frac{1}{12} m^4 - hm + \ldots \ . \end{split}\]

Ajuste\(\frac{\pz f}{\pz m}=0\), obtenemos

\[\frac{1}{3} m^3 + (\theta-1)\cdot m - h =0\ . \label{IMFmheqn}\]

Si\(\theta>1\) entonces tenemos una solución\(m=h/(\theta-1)\). El\(m^3\) término puede ser ignorado porque es de orden superior en\(h\), y hemos asumido\(h\ll |\theta-1|\ll 1\). Esto se conoce como la ley Curie-Weiss ¹⁰. La susceptibilidad magnética se comporta como

\[\xhi(\theta)={\pz m\over\pz h}={1\over \theta-1} \propto |\theta-1|^{-\gamma}\ ,\]

donde está el exponente\(\gamma\) crítico de magnetización\(\gamma=1\). Si\(\theta<1\) entonces mientras todavía hay una solución en\(m=h/(\theta-1)\), se encuentra en un máximo local de la energía libre, como se muestra en la Figura\(\PageIndex{2}\). El mínimo de la energía libre se produce cerca de la\(h=0\) solución\(m=m\ns_0(\theta)\equiv \sqrt{3}\,(1-\theta)\), y la escritura\(m=m\ns_0+\delta m\) nos encontramos\(\delta m\) con orden lineal en\(h\) as\(\delta m(\theta,h)=h/2(1-\theta)\). Por lo tanto,

\[m(\theta,h)=\sqrt{3}\,(1-\theta)^{1/2} +{h\over 2(1-\theta)}\ .\]

Una vez más, encontramos que\(\xhi(\theta)\) diverge como\(|\theta-1|^{-\gamma}\) con\(\gamma=1\). El exponente\(\gamma\) a cada lado de la transición es el mismo.

Por último, podemos establecer\(\theta=\theta\ns_\Rc\) y examinar\(m(h)\). Encontramos, a partir de la Ecuación\ ref {IMFMHeqn},

\[m(\theta=\theta\ns_\Rc,h)=(3h)^{1/3}\propto h^{1/\delta}\ ,\]

donde\(\delta\) hay un nuevo exponente crítico. La teoría media del campo da\(\delta=3\). Tenga en cuenta que en\(\theta=\theta\ns_\Rc=1\) tenemos\(m=\tanh(m+h)\), e invirtiendo encontramos

\[h(m,\theta=\theta\ns_\Rc)=\half\ln\!\bigg({1+m\over 1-m}\bigg)-m={m^3\over 3} + {m^5\over 5} + \ldots \ ,\]

lo cual es congruente con lo que acabamos de encontrar\(m(h,\theta=\theta\ns_\Rc)\).

Tabla Exponentes\(\PageIndex{1}\): críticos de la teoría de campos medios comparados con resultados exactos para el modelo bidimensional de Ising, resultados numéricos para el modelo tridimensional de Ising y experimentos sobre la transición líquido-gas en CO\({}_2\). Fuente: H. E. Stanley, Transiciones de fase y fenómenos críticos.

		Ising 2D	Ising 3D	CO\({}_2\)
Exponente	MFT	(exacto)	(numérica)	\ ({} _2\)” style="text-align:center; vertical-align:middle; "> (expt.)
\(\alpha\)	\(0\)	\(0\)	\(0.125\)	\ ({} _2\)” style="text-align:center; vertical-align:middle; ">\( 0.1\)
\(\beta\)	\(1/2\)	\(1/8\)	\(0.313\)	\ ({} _2\)” style="text-align:center; vertical-align:middle; ">\(0.35\)
\(\gamma\)	\(1\)	\(7/4\)	\(1.25\)	\ ({} _2\)” style="text-align:center; vertical-align:middle; ">\(1.26\)
\(\delta\)	\(3\)	\(15\)	\(5\)	\ ({} _2\)” style="text-align:center; vertical-align:middle; ">\(4.2\)

¿Qué tan bien le va a la teoría de campos medios al describir la transición de fase del modelo de Ising? En la tabla \(\PageIndex{1}\)comparamos nuestros resultados medios de campo para los exponentes\(\alpha\)\(\beta\),\(\gamma\), y\(\delta\) con valores exactos para el modelo bidimensional de Ising, trabajo numérico en el modelo tridimensional de Ising y experimentos sobre la transición líquido-gas en CO\({}_2\). Lo primero que hay que señalar es que los exponentes dependen de la dimensión del espacio, y esto es algo que la teoría de campo media pierde por completo. De hecho, resulta que los exponentes medios de campo son exactos proporcionados\(d>d\ns_\Ru\), donde\(d\ns_\Ru\) está la dimensión crítica superior de la teoría. Para el modelo de Ising\(d\ns_\Ru=4\),, y por encima de cuatro dimensiones (que por supuesto no es física) los exponentes medios de campo son de hecho exactos. Vemos que, en general, los resultados de MFT se comparan mejor con los valores de exponentes tridimensionales que con los bidimensionales, esto tiene sentido ya que MFT funciona mejor en dimensiones superiores. La razón de esto es que mayores dimensiones significan más vecinos más cercanos, lo que tiene el efecto de reducir la importancia relativa de las fluctuaciones que descuidamos incluir.

Dinámica de magnetización

Los procesos disipativos impulsan los sistemas físicos a estados mínimos de energía. Podemos modelar crudamente la dinámica disipativa de un imán escribiendo la ecuación fenomenológica

\[{dm\over ds}=-{\pz f\over\pz m}\ , \label{IMFmdyn}\]

donde\(s\) es una variable de tiempo adimensional. Bajo estas dinámicas, la energía libre nunca va en aumento:

\[{df\over ds}={\pz f\over\pz m}\,{\pz m\over\pz s}=-\bigg({\pz f\over\pz m}\bigg)^{\!2}\le 0\ .\]

Claramente el punto fijo de estas dinámicas, donde\({\dot m}=0\), es una solución a la ecuación del campo medio\({\pz f\over\pz m}=0\).

Figura\(\PageIndex{3}\): Dinámica disipativa de magnetización\({\dot m}=-f'(m)\). El panel inferior muestra\(h^*(\theta)\) de la Ecuación\ ref {IMFHStar}. Porque\((\theta,h)\) dentro de la región sombreada azul, la energía libre\(f(m)\) tiene un mínimo global más un mínimo local y un máximo local. De lo contrario solo\(f(m)\) tiene un mínimo global único. Los paneles superiores muestran una bifurcación imperfecta en la dinámica de magnetización en\(h=0.0215\), para lo cual\(\theta^*=0.90\). Temperaturas mostradas:\(\theta=0.65\) (azul),\(\theta=\theta^*(h)=0.90\) (verde) y\(\theta=1.2\). El punto fijo estable más a la derecha corresponde al mínimo global de la energía libre. La parte inferior de los dos paneles superiores del medio muestra\(h=0\), donde tanto los atractivos puntos fijos como el punto fijo repulsivo se fusionan en un único punto fijo atractivo (bifurcación de horca supercrítica).

El flujo de fase para la ecuación\({\dot m}=-f'(m)\) se muestra en la Figura\(\PageIndex{3}\). Como hemos visto, para cualquier valor de\(h\) hay una temperatura por\(\theta^*\) debajo de la cual la energía libre\(f(m)\) tiene dos mínimos locales y un máximo local. Cuando\(h=0\) los mínimos son degenerados, pero al finito\(h\) uno de los mínimos es un mínimo global. Así, pues\(\theta<\theta^*(h)\) hay tres soluciones a las ecuaciones de campo medio. En el lenguaje de los sistemas dinámicos, bajo la dinámica de la Ecuación\ ref {IMFMdyn}, los mínimos de\(f(m)\) corresponden a puntos fijos atractivos y máximos a puntos fijos repulsivos. Si\(h>0\), el más a la derecha de estos puntos fijos corresponde al mínimo global de la energía libre. A medida\(\theta\) que se incrementa, este punto fijo evoluciona suavemente. At\(\theta=\theta^*\), el mínimo local (metaestable) y el máximo local se fusionan y aniquilan en una bifurcación de nota de silla de montar. Sin embargo, en\(h=0\) los tres puntos fijos se fusionan\(\theta=\theta\ns_\Rc\) y la bifurcación es una horca supercrítica. \(t\)En función de lo finito\(h\), se dice que la dinámica exhibe una bifurcación imperfecta, que es una horca supercrítica deformada.

Figura Panel\(\PageIndex{4}\): superior: histéresis en función de la rampa del campo magnético adimensional\(h\) en\(\theta=0.40\). Flechas de color rojo oscuro debajo de la curva siguen la evolución de la magnetización en lento aumento de\(h\). Las flechas de color gris oscuro por encima de la curva siguen la evolución de la magnetización al disminuir lentamente de\(h\). Panel inferior: solución establecida para\(m(\theta,h)\) en función de\(h\) a temperaturas\(\theta=0.40\) (azul),\(\theta=\theta_\Rc=1.0\) (verde oscuro) y\(t=1.25\) (rojo).

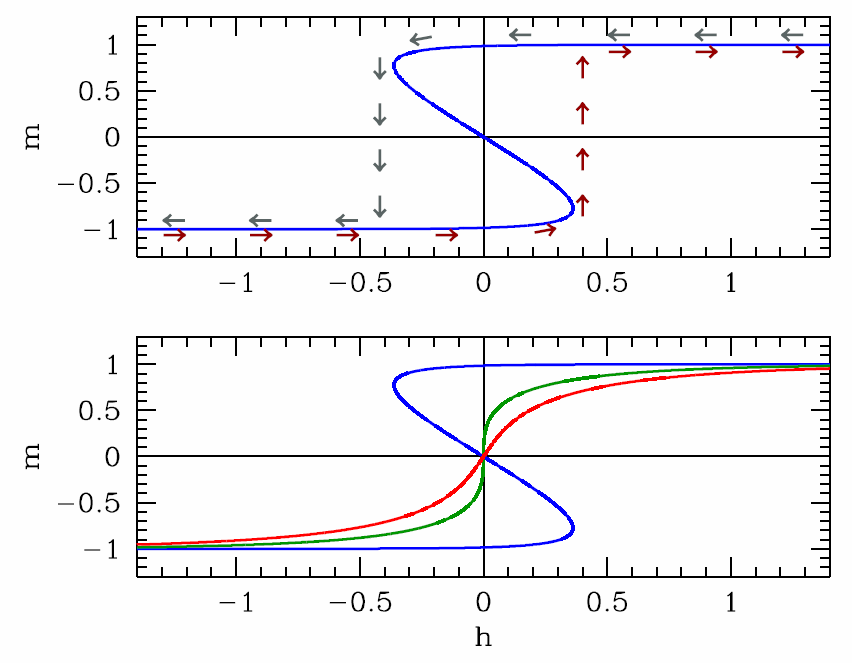
El conjunto de soluciones para la ecuación de campo medio se expresa simplemente invirtiendo la\(\tanh\) función a obtener\(h(\theta,m)\). Uno encuentra fácilmente

\[h(\theta,m)={\theta\over 2}\,\ln\!\bigg({1+m\over 1-m}\bigg)-m\ .\]

Como vemos en el panel inferior de la Figura\(\PageIndex{4}\),\(m(h)\) se vuelve multivalor para\(h\in\big[-h^*(\theta)\,,\,+h^*(\theta)\big]\), donde\(h^*(\theta)\) se da en la Ecuación\ ref {IMFHStar}. Ahora imagínese eso\(\theta<\theta\ns_\Rc\) y lentamente hacemos rampa el campo\(h\) de un gran valor negativo a un gran valor positivo, y luego lentamente retrocedemos a su valor original. En la escala de tiempo de la dinámica de magnetización, podemos considerar\(h(s)\) como una constante. (Recuerde que la variable de tiempo está\(s\) aquí.) Así,\(m(s)\) fluirá al punto fijo estable más cercano. Inicialmente el sistema comienza con\(m=-1\) y\(h\) grande y negativo, y solo hay un punto fijo, a\(m^*\approx -1\). A medida que aumenta\(h\) lentamente, el valor del punto fijo\(m^*\) también aumenta lentamente. A medida que\(h\) excede\(-h^*(\theta)\), se produce una bifurcación de nodo de silla de montar y se crean dos nuevos puntos fijos en positivo\(m\), uno estable y otro inestable. El mínimo global de la energía libre sigue estando en el punto fijo con\(m^*<0\). Sin embargo, cuando se\(h\) cruza\(h=0\), el mínimo global de la energía libre se encuentra en el punto fijo más positivo\(m^*\). La dinámica, sin embargo, mantiene al sistema atascado en lo que es una fase metaestable. Esto persiste hasta\(h=+h^*(\theta)\), momento en el que ocurre otra bifurcación de la nota de silla de montar, y el atractivo punto fijo en\(m^*<0\) aniquila con el punto fijo repulsivo. La dinámica entonces actúa rápidamente para conducir\(m\) al único punto fijo restante. Este proceso se representa en el panel superior de la Figura\(\PageIndex{4}\). Como se puede ver en la figura, el sistema sigue un punto fijo estable hasta que el punto fijo desaparece, aunque ese punto fijo no siempre corresponda a un mínimo global de la energía libre. La\(m(h)\) curva resultante no es reversible en función del tiempo, y posee una forma característica conocida como bucle de histéresis. Etimológicamente, la palabra histéresis deriva del griego\(\ups\sigma\tau\ve\rho\eta\sigma\iota\varsigma\), que significa 'rezagado detrás'. Los sistemas histeréticos exhiben una dependencia histórica de su estado, lo que no está determinado únicamente por condiciones externas. Se puede exhibir histéresis con respecto a cambios en el campo magnético aplicado, cambios en la temperatura o cambios en otros parámetros determinados externamente.

Más allá de vecinos más cercanos

Supongamos que hubiéramos empezado con el modelo más general,

\[\begin{split} \HH&=-\sum_{i<j} J\ns_{ij}\,\sigma\ns_i\,\sigma\ns_j - H\sum_i\sigma\ns_i\\ &=-\half\sum_{i\ne j} J\ns_{ij}\,\sigma\ns_i\,\sigma\ns_j - H\sum_i\sigma\ns_i\ , \end{split}\]

donde\(J_{ij}\) esta el acoplamiento entre giros en sitios\(i\) y\(j\). En la ecuación superior anterior, cada par\((ij)\) se cuenta una vez en el término de interacción; esto puede ser reemplazado por una suma sobre todo\(i\) y\(j\) si incluimos un factor de\(\half\). ¹¹ El campo medio resultante Hamiltoniano es entonces

\[\HH\ns_{\ssr{MF}}=\half N\jhz\,m^2- \big(H+\jhz\,m\big)\sum_i\sigma_i\ .\]

Aquí,\({\hat J}(\Bq)\) está la transformada de Fourier de la matriz de interacción\(J\ns_{ij}\): ¹²

\[{\hat J}(\Bq)=\sum_\BR J(\BR)\,e^{-i\Bq\cdot\BR}\ .\]

Solo para las interacciones de vecinos más cercanos, se tiene\(\jhz=zJ\), donde\(z\) está el número de coordinación de celosía, el número de vecinos más cercanos de cualquier sitio dado. La energía libre escalada es como en la Ecuación\ ref {fergsca}, con\(f=F/N\jhz\),\(\theta=\kT/\jhz\), y\(h=H/\jhz\). El análisis procede precisamente como antes, y concluimos\(\theta\ns_\Rc=1\),\(\kB T^{\ssr{MF}}_\Rc=\jhz\).

Modelo Ising con fuerzas de largo alcance

Considera un modelo de Ising donde\(J\ns_{ij}=J/N\) para todos\(i\) y\(j\), para que haya una interacción muy débil entre cada par de giros. El hamiltoniano es entonces

\[\HH=-{J\over 2N}\bigg(\sum_i\sigma\ns_i\bigg)^{\!2} - H\sum_k\sigma\ns_k\ .\]

La función de partición es

\[Z= \Tra_{\{\sigma_i\}}\,\exp\!\Bigg[ {\beta J\over 2N}\bigg(\sum_i\sigma\ns_i\bigg)^{\!2} + \beta H\sum_i\sigma\ns_i\Bigg]\ .\]

Ahora invocamos la integral gaussiana,

\[\int\limits_{-\infty}^\infty\!\!\!dx\>e^{-\alpha x^2 - \beta x}=\sqrt{\pi\over\alpha\,}\>e^{\beta^2/4\alpha}\ .\]

Por lo tanto,

\[\exp\!\Bigg[ {\beta J\over 2N}\bigg(\sum_i\sigma\ns_i\bigg)^{\!2}\Bigg]=\bigg({N\beta J\over 2\pi}\bigg)^{\!\!1/2}\! \int\limits_{-\infty}^\infty\!\!\!dm\>e^{-{1\over 2} N\beta J m^2 + \beta J m\sum_i\sigma\ns_i}\ ,\]

y podemos escribir la función de partición como

\[\begin{split} Z&=\bigg({N\beta J\over 2\pi }\bigg)^{\!\!1/2}\!\int\limits_{-\infty}^\infty\!\!\!dm\>e^{-{1\over 2} N\beta J m^2} \bigg(\sum_\sigma e^{\beta(H+Jm)\sigma}\bigg)^{\!N}\\ &=\bigg({N\over 2\pi \theta}\bigg)^{\!\!1/2}\!\int\limits_{-\infty}^\infty\!\!\!dm\>e^{-N A(m)/\theta}\ , \end{split}\]

donde\(\theta=\kT/J\)\(h=H/J\), y

\[A(m)=\half m^2-\theta\ln\! \left[2\cosh \bigg({h+m\over\theta}\bigg)\right]\ .\]

Ya que\(N\to\infty\), podemos realizar la integral utilizando el método de los descensos más empinados. Por lo tanto, debemos establecer

\[{dA\over dm}\bigg|\nd_{m^*}=0 \quad\Longrightarrow\quad m^*=\tanh\bigg({m^*+h\over\theta}\bigg)\ .\]

Ampliando sobre\(m=m^*\), escribimos

\[A(m)=A(m^*) + \half A''(m^*)\,(m-m^*)^2 + \frac{1}{6}\,A'''(m^*)\,(m-m^*)^3 + \ldots\ .\]

Al realizar las integraciones, obtenemos

\[\begin{split} Z&=\bigg({N\over 2\pi\theta}\bigg)^{1/2} e^{-NA(m^*)/\theta}\!\!\int\limits_{-\infty}^\infty\!\!\!d\nu\> \exp\!\Bigg[-{N A''(m^*)\over 2\theta}\>m^2 - {NA'''(m^*)\over 6\theta}\>m^3 + \ldots\Bigg]\\ &={1\over\sqrt{A''(m^*)}}\>e^{-NA(m^*)/\theta}\cdot\Big\{ 1 + \CO(N^{-1})\Big\}\ . \end{split}\]

La energía libre correspondiente por sitio

\[f={F\over NJ}=A(m^*)+{\theta\over 2N}\,\ln A''(m^*) + \CO(N^{-2})\ ,\]

donde\(m^*\) está la solución a la ecuación de campo medio que minimiza\(A(m)\). ¡La teoría del campo medio es exacta para este modelo!