1.3: Ecuación de Estado

La Ecuación de Estado de Gas Ideal

Al especificar la ecuación de estado, utilizaremos la temperatura absoluta, denotada por\(t\). Vamos a introducir este concepto más adelante, pero por ahora, lo tomaremos como se ha dado. La temperatura absoluta es siempre positiva, variando de cero (o cero absoluto) a infinito. El gas ideal se caracteriza entonces por la ecuación de estado

\[p\,V=n\,k\,T\]

donde\(N\) denota el número de moléculas del gas y\(k\) es una constante, conocida como constante de Boltzmann. Otra forma de escribir esto es la siguiente. Definimos el número de Avogadro como\(6.02214 \times 10^{23}\). Este número se produce de la siguiente manera. La masa de un átomo se debe principalmente a los protones y neutrones en su núcleo. Cada protón tiene una masa de\(1.6726×10^{−24} gm\), cada neutrón tiene una masa de\(1.6749×10^{−24} gm\). Si descuidamos la diferencia de masa entre el protón y el neutrón, la masa de un átomo de peso atómico\(A\) (= número de protones + número de neutrones en el núcleo) viene dada por\(A \times 1.6726 \times 10^{−24} gm\). Así, si tomamos\(A\) gramos del material, el número de átomos viene dado por\((1.67 \times 10^{−24})^{−1} ≈ 6 × 10^{23}\). Este es esencialmente el número de Avogadro. La diferencia de masa entre el protón y el neutrón no es completamente despreciable y también hay ligeras variaciones de un tipo de núcleo a otro debido a las energías de unión variables de los protones y neutrones. Por lo que estandarizamos el número Avogadro definiéndolo como\(6.02214 \times 10^{23}\), que está muy cerca del número de átomos en\(12\, gm\) del isótopo\(C^{12}\) de carbono (que se utilizó para estandarizar las masas atómicas).

Si tenemos\(N\) moléculas de un material, decimos que tiene\(n\) moles del material, dónde\(n = \frac{N}{\text{Avogadro Number}}\). Así podemos reescribir la ecuación de gas ideal de estado como

\[p\,V=n\,R\,T, \quad R=k\,(\text{Avogadro Number})\]

Numéricamente, tenemos, en julios por unidad Kelvin de temperatura,

\[k≈1.38065 \times 10^{-23}\,\frac{J}{K} , \quad R≈8.3145\,\frac{J}{\text{mole}\;K}\]

La ecuación de estado de van der Waals

La ley de gas ideal nunca se obtiene para los gases reales. Hay fuerzas intermoleculares que cambian la ecuación de estado, sin mencionar la naturaleza cuántica de la dinámica de las moléculas que adquiere mayor importancia a bajas temperaturas. La ecuación de estado puede en principio ser calculada o determinada a partir de las fuerzas intermoleculares en la mecánica estadística. Las correcciones a la ley del gas ideal pueden expresarse como series de términos conocidos como expansión virial, siendo el segundo coeficiente virial la primera corrección de este tipo. Si bien el método es general, los específicos dependen de la naturaleza de las moléculas y una fórmula simple no es fácil de anotar.

Figura\(\PageIndex{1}\): La forma general del potencial intermolecular en función de la distancia

Una ecuación de estado que captura algunas características muy generales de las fuerzas intermoleculares fue escrita por van der Waals, en la década de 1870, mucho antes de que se desarrollara la expansión virial. Es importante porque da una buena aproximación de trabajo para muchos gases. La ecuación de estado de van der Waals es

\[(p + \frac{aN^2}{V^2})(V − bN) = NkT \label{1.3.4}\]

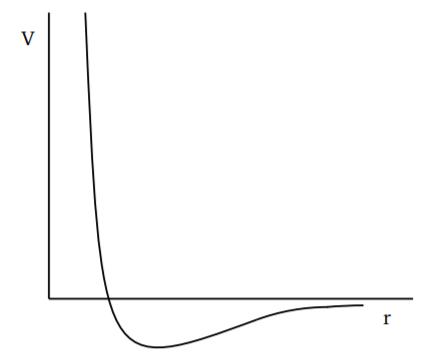
El razonamiento detrás de esta ecuación es el siguiente. En general, las fuerzas intermoleculares tienen una repulsión de corto alcance, ver Fig. 1.3.1. Esto evita que las moléculas formen estados unidos. La formación de estados unidos sería una reacción química, por lo que realmente estamos considerando gases donde no hay más reacción química más allá de la formación inicial de las moléculas. Por ejemplo, si consideramos el oxígeno, dos átomos de oxígeno se unen para formar la molécula de oxígeno\(O_2\), pero no hay unión para que dos moléculas\(O_2\) de oxígeno (dos) formen algo más complicado. A nivel potencial, esto se debe a una repulsión de corto alcance que impide que se unan. En el razonamiento de van der Waals, tal efecto podría incorporarse argumentando que el volumen completo no\(V\) está disponible para las moléculas, un cierto volumen\(b\) alrededor de cada molécula está excluido de ser accesible a otras moléculas. Por lo que debemos sustituir\(V\) por\((V − bN)\) en la ley de gas ideal.

Las fuerzas intermoleculares también tienen una parte atractiva en separaciones ligeramente mayores. Esta atracción llevaría a que las moléculas se unieran, reduciendo así la presión. Entonces, la presión calculada asumiendo que las moléculas no interaccionan, que es la presión cinética\(p_{kin}\), debe estar relacionada con la presión real\(p\) por

\[p=p_{kin}−\frac{aN^2}{V^2} \label{1.3.5}\]

La interacción es principalmente por pares, por lo que esperamos un factor de\(\frac{N(N − 1)}{2}\) (que es el número de emparejamientos que uno puede hacer) para\(N\) las moléculas. Esto va como ∼\(N^2\), lo que explica el segundo término en la Ecuación\ ref {1.3.5}. Usando la ley de gas ideal para\(p_{\text{kin}}\) con el volumen\((V − bN)\), obtenemos la Ecuación\ ref {1.3.4}. En esta ecuación,\(a\) y\(b\) se encuentran parámetros específicos del gas en consideración.