2.3: Fórmula Barométrica y Velocidad del Sonido

Aquí consideramos dos ejemplos simples del uso de la ley de gas ideal y la fórmula para la expansión adiabática.Primero, considere la fórmula barométrica que da la densidad (o presión) del aire a una altura\(h\) por encima de la superficie de la Tierra (también llamada principio de Pascal). Asumimos equilibrio completo, mecánico y térmico. El argumento se ilustra en la Figura\(\PageIndex{1}\).

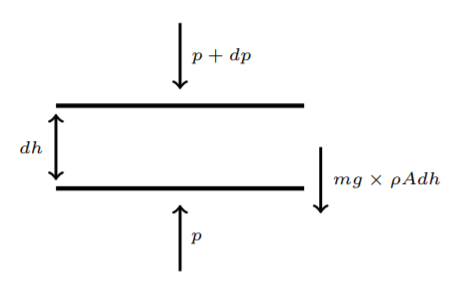Figura\(\PageIndex{1}\): Coincidencia de fuerzas para fórmula barométrica

Consideramos una capa de aire, con área transversal horizontal\(A\) y altura\(dh\). Si tomamos las moléculas para tener una masa\(m\) y la densidad numérica de partículas a ser\(\rho\), entonces el peso de esta capa de aire es\(mg × \rho Adh\). Esta es la fuerza que actúa hacia abajo. Se compensa con la diferencia de presión entre el límite superior y el límite inferior para esta capa. Este último es así\(dp \times A\), actuando de nuevo a la baja, tal y como lo hemos dibujado. La fuerza total siendo cero para el equilibrio, obtenemos

\[dp\;A + mg\rho Adh = 0\]

Así, la variación de la presión con la altura viene dada por

\[\frac{dp}{dh} = −mg \rho\]

Supongamos la ley ideal del gas para el aire; esto no es perfecto, pero es una aproximación razonablemente buena. Entonces\(p = \frac{NkT}{V} = ρkT\) y la ecuación anterior se convierte

\[\frac{dp}{dh} = −\frac{mg}{kT}p\]

La solución es

\[p = p_0 \exp \left(−\dfrac{mgh}{kT} \right),\]

o

\[ρ = ρ_0 \exp \left(−\dfrac{mgh}{kT} \right) \label{2.3.4} \]

Este argumento es, sin duda, crudo. En realidad, la temperatura también varía con la altura. Además, existen tantos procesos de no equilibrio (como viento, calentamiento por absorción de radiación solar, variación de temperatura entre el día y la noche, etc.) en la atmósfera que la Ecuación\ ref {2.3.4} sólo puede ser válida para un rango corto de altura y sobre una pequeña área de equilibrio local.

Nuestro siguiente ejemplo es sobre la velocidad del sonido. Para ello, podemos tratar el medio, digamos, aire, como un fluido, caracterizado por una densidad numérica\(ρ\) y una velocidad de flujo\(\vec{v}\). Las ecuaciones para el fluido son

\[\begin{align} \frac{∂ρ}{∂t} + ∇ · (ρ \vec{v}) &= 0 \label{eq:A}\\[4pt] \frac{∂\vec{v}}{∂t} + v_i∂_i\vec{v} &= −\frac{∇p}{ρ} \label{eq:B}\end{align}\]

La ecuación\ ref {EQ:a} es la ecuación de continuidad que expresa la conservación del número de partículas, o masa, si multiplicamos la ecuación por la masa de una molécula. La ecuación\ ref {EQ:b} es el equivalente fluido de la segunda ley de Newton. A falta de fuerzas externas, todavía podemos tener términos de fuerza; de hecho, el gradiente de la presión, como se ve desde la ecuación, actúa como término de fuerza. Esto también puede ser reexpresado en términos de la densidad, ya que la presión y la densidad están relacionadas por la ecuación de estado.

Ahora considere el medio en equilibrio sin ondas sonoras en él. La presión de equilibrio debe ser uniforme; denotamos esto por\(p_0\), con la densidad uniforme correspondiente como\(ρ_0\). Además, tenemos\(\vec{v} = 0\) en equilibrio. Ahora podemos considerar las ondas sonoras como perturbaciones sobre este fondo, escribiendo

\[\begin{align*} ρ &= ρ_0 + δρ \\[4pt] p &= p_0 + δρ \left(\frac{∂p}{∂ρ}\right)_0 \\[4pt] \vec{v} &= 0 + \vec{v} \end{align*}\]

Tratando\(δρ\) y\(\vec{v}\) siendo de primer orden en la perturbación, las ecuaciones fluidas pueden aproximarse como

\[\begin{align*} \frac{∂}{∂t}(δρ) &≈ −ρ_0 ∇ · \vec{v} \\[4pt] \frac{∂\vec{v}}{∂t} &≈ − \frac{1}{ρ_0} \left(\frac{∂p}{∂ρ}\right)_0 ∇δρ \end{align*}\]

Tomando la derivada de la primera ecuación y usando la segunda, encontramos

\[\left(\frac{∂^2}{∂t^2} − c_s^2 ∇^2\right) δρ = 0 \label{2.3.8}\]

donde

\[c_s^2= \left(\frac{∂p}{∂ρ}\right)_0\]

La ecuación\ ref {2.3.8} es la ecuación de onda con la velocidad de propagación dada por\(c_s\). Esta ecuación muestra que las perturbaciones de densidad pueden viajar como ondas; estas son las ondas sonoras. Es fácil verificar que la ecuación de onda tiene soluciones onduladas de la forma

\[δρ = A\cos(ωt − \vec{k} · \vec{x}) + B\sin(ωt − \vec{k} · \vec{x})\]

con\(ω^2 = c_s^2 \vec{k} · \vec{k}\). Esto nuevamente se identifica\(c_s\) como la velocidad de propagación de la onda.

Podemos calcular la velocidad de las ondas sonoras de manera más explícita usando la ecuación de estado. Si tomamos aire para obedecer la ley de gas ideal, tenemos\(p = ρ kT\). Si el proceso de compresión y descompresión que constituye la onda sonora es isotérmico, entonces

\[\left(\frac{∂p}{∂ρ}\right)_0 = \frac{p_0}{ρ_0}.\]

En realidad, la escala de tiempo para la compresión y descompresión en una onda sonora suele ser muy corta en comparación con el tiempo necesario para una termalización adecuada, por lo que es más preciso tratarla como un proceso adiabático. En este caso, tenemos

\[pV^{\gamma} = \text{constant}\]

para que

\[c_s^2= \left(\frac{∂p}{∂ρ}\right)_0 = \gamma\frac{p_0}{ρ_0}\]

Ya que\(\gamma > 1\), esto da una velocidad superior a la que se obtendría en un proceso isotérmico. Experimentalmente, se puede demostrar que esta fórmula para la velocidad del sonido es lo que se obtiene, demostrando que las ondas sonoras resultan de un proceso adiabático.