2.1: Tutorial de Matemáticas — Vectores

Figura\(\PageIndex{2}\): .1: Vectores de desplazamiento en un plano. El vector A representa el desplazamiento de George de Mary, mientras que el vector B representa el desplazamiento de Paul de George. El vector C representa el desplazamiento de Pablo de María y C = A + B. Las cantidades A _x, A _y, etc., representan los componentes cartesianos de los vectores.

Figura\(\PageIndex{2}\): .2: Croquis de definición para el ángulo θ que representa la orientación de un vector bidimensional.

Antes de continuar, necesitamos explorar la idea de un vector. Un vector es una cantidad que expresa tanto la magnitud como la dirección. Gráficamente representamos un vector como una flecha. En la notación de tipografía un vector está representado por un carácter de negritas, mientras que en escritura a mano se dibuja una flecha sobre el carácter que representa el vector.

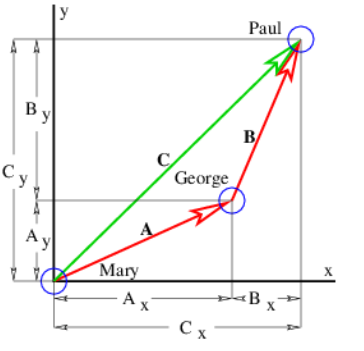
La Figura 2.1 muestra algunos ejemplos de vectores de desplazamiento, es decir, vectores que representan el desplazamiento de un objeto de otro, e introduce la idea de adición de vectores. La cola del vector B se coloca con la cabeza del vector A, y el vector que se extiende desde la cola de A a la cabeza de B es la suma de A y B, llamada C en la figura 2.1.

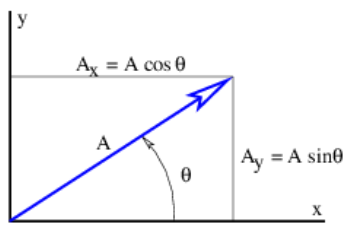
Las cantidades\(A_{x}, A_{y}\) etc., representan los componentes cartesianos de los vectores en la figura 2.1. Un vector se puede representar ya sea por sus componentes cartesianos, que son solo las proyecciones del vector sobre los ejes de coordenadas cartesianas, o por su dirección y magnitud. La dirección de un vector en dos dimensiones generalmente se representa por el ángulo antihorario del vector con respecto al eje x, como se muestra en la figura 2.2. La conversión de una forma a otra viene dada por las ecuaciones

\[A=\left(A_{x}^{2}+A_{y}^{2}\right)^{1 / 2} \quad \theta=\tan ^{-1}\left(A_{y} / A_{x}\right)\label{2.1}\]

\[A_{x}=A \cos (\theta) \quad A_{y}=A \sin (\theta)\label{2.2}\]

donde A es la magnitud del vector. Una magnitud vectorial a veces se representa por notación de valor absoluto: A ≡| A |.

Observe que la tangente inversa da un resultado que es ambiguo relativo a sumar o restar múltiplos enteros de π. Así, el cuadrante en el que se encuentra el ángulo debe resolverse examinando independientemente los signos de A _{x y} A y eligiendo el valor apropiado de θ.

Para agregar dos vectores, A y B, es más fácil convertirlos a forma de componente cartesiano. Los componentes de la suma C = A + B son entonces solo las sumas de los componentes:

\[C_{x}=A_{x}+B_{x} \quad C_{y}=A_{y}+B_{y}\label{2.3}\]

La resta de vectores se realiza de manera similar, por ejemplo, si A = C - B, entonces

\[A_{x}=C_{x}-B_{x} \quad A_{y}=C_{y}-B_{y}\label{2.4}\]

Un vector unitario es un vector de longitud unitaria. Siempre se puede construir un vector unitario a partir de un vector ordinario (distinto de cero) dividiendo el vector por su longitud: n = A | A |. Esta operación de división se lleva a cabo dividiendo cada uno de los componentes vectoriales por el número en el denominador. Alternativamente, si el vector se expresa en términos de longitud y dirección, la magnitud del vector se divide por el denominador y la dirección no cambia.

Los vectores unitarios se pueden utilizar para definir un sistema de coordenadas cartesianas. Convencionalmente, i, j y k indican los ejes x, y y z de dicho sistema. Tenga en cuenta que i, j y k son mutuamente perpendiculares. Cualquier vector puede ser representado en términos de vectores unitarios y sus componentes cartesianos: A = A _x i + A _y j + A _z k. Una forma alternativa de representar un vector es como una lista de componentes: A = (A _x, A _y, A _z). Tendemos a utilizar esta última representación ya que es una notación algo más económica.

Hay dos formas de multiplicar dos vectores, dando respectivamente lo que se conoce como el producto punto y el producto cruzado. El producto cruzado produce otro vector mientras que el producto de punto produce un número. Aquí discutiremos solo el producto punto. El producto cruzado se presentará más adelante cuando sea necesario.

Figura 2.3: Croquis de definición para producto punto.

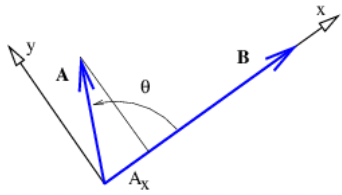
Dados los vectores A y B, el producto de punto de los dos se define como

\[\mathbf{A} \cdot \mathbf{B} \equiv|\mathbf{A} \| \mathbf{B}| \cos \theta\label{2.5}\]

donde θ es el ángulo entre los dos vectores. En dos dimensiones existe una expresión alternativa para el producto punto en términos de los componentes cartesianos de los vectores:

\[\mathbf{A} \cdot \mathbf{B}=A_{x} B_{x}+A_{y} B_{y}\label{2.6}\]

Es fácil demostrar que esto es equivalente a la forma coseno del producto punto cuando el eje x se encuentra a lo largo de uno de los vectores, como en la figura 2.3. Observe en particular que A _x = | A | cos θ, mientras que B _x = | B | y B _y = 0. Así, A ⋅ B = | A | cos θ | B | en este caso, que es idéntica a la forma dada en la ecuación (2.5).

Figura\(\PageIndex{2}\): .4: Figura de definición para el sistema de coordenadas giradas. El vector R tiene los componentes X e Y en el sistema de coordenadas no cebado y los componentes X′ e Y′ en el sistema de coordenadas cebado.

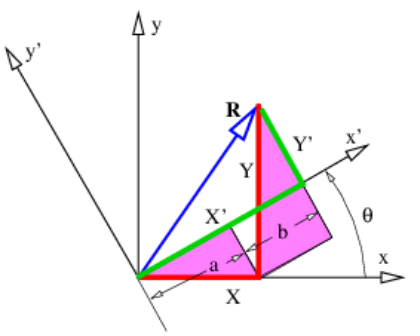
Todo lo que queda por probar para que la Ecuación\ ref {2.6} se mantenga en general es mostrar que produce la misma respuesta independientemente de cómo se orienta el sistema de coordenadas cartesianas en relación con los vectores. Para ello, debemos mostrar que A _{x B x} + A _y B _y = A _x ′ B _x ′ + A _y ′ B _y ′, donde los primos indican componentes en un sistema de coordenadas girado desde el sistema de coordenadas original.

La Figura 2.4 muestra el vector R resuelto en dos sistemas de coordenadas girados uno con respecto al otro. A partir de esta cifra queda claro que\(X^{\prime}=a+b\). Centrándonos en los triángulos sombreados, eso lo vemos\(a=X \cos \theta \text { and } b=Y \sin \theta\). Así, nos encontramos\(X^{\prime}=X \cos \theta+Y \sin \theta\). Razonamiento similar lo demuestra\(Y^{\prime}=-X \sin \theta+Y \cos \theta\). Sustituyendo estos y usando la identidad trigonométrica cos ² θ + sin ² θ = 1 da como resultado

\ [\ begin {ecuación}
\ begin {alineada}
A_ {x} ^ {\ prime} B_ {x} ^ {\ prime} +A_ {y} ^ {\ prime} B_ {y} ^ {\ prime} &=\ left (A_ {x}\ cos\ theta+a_ {y}\ sin\ theta\ derecha)\ izquierda (B_ {x}\ cos\ theta+a_ {y}\ sin\ theta\ derecha)\ izquierda (B_ {x}\ cos\ theta\ theta+b_ {y}\ sin\ theta\ derecha)\\
&+\ izquierda (-A_ {x}\ sin\ theta+a_ {y}\ cos\ theta\ derecha)\ izquierda (-B_ {x} \ sin\ theta+B_ {y}\ cos\ theta\ derecha)\\
&=A_ {x} B_ {x} +A_ {y} B_ {y}
\ final {alineado}
\ final {ecuación}\ etiqueta {2.7}\]

demostrando así la equivalencia completa de las dos formas del producto punto según lo dado por las ecuaciones (2.5) y (2.6). Multiplique la expresión anterior para verificar esto.

Una cantidad numérica que no depende del sistema de coordenadas que se esté utilizando se llama escalar. El producto punto de dos vectores es un escalar. Sin embargo, los componentes de un vector, tomados individualmente, no son escalares, ya que los componentes cambian a medida que cambia el sistema de coordenadas. Dado que las leyes de la física no pueden depender de la elección del sistema de coordenadas que se utilice, insistimos en que las leyes físicas se expresen en términos de escalares y vectores, pero no en términos de los componentes de los vectores.

En tres dimensiones la forma coseno del producto punteado sigue siendo la misma, mientras que la forma componente es

\[\mathbf{A} \cdot \mathbf{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z}\label{2.8}\]