2.2: Ondas Planas

Una onda plana en dos o tres dimensiones es como una onda sinusoidal en una dimensión, excepto que las crestas y los canales no son puntos, sino que forman líneas (2-D) o planos (3-D) perpendiculares a la dirección de propagación de la onda. La figura\(\PageIndex{1}\) muestra una onda sinusoidal plana en dos dimensiones. La flecha grande es un vector llamado vector de onda, que define (1) la dirección de propagación de la onda por su orientación perpendicular a los frentes de onda, y (2) el número de onda por su longitud.

Figura\(\PageIndex{1}\): Croquis de definición para una onda sinusoidal plana en dos dimensiones. Los frentes de onda son superficies de fase constantes separadas por una longitud de onda. El vector de onda es normal a los frentes de onda y su longitud es el número de onda.

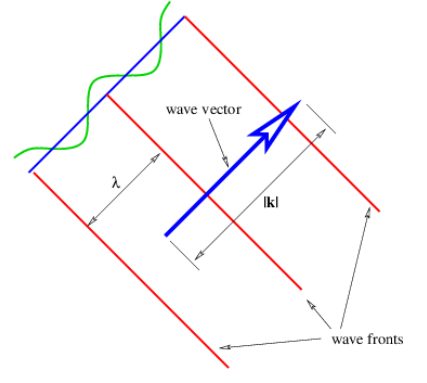
Podemos pensar en un frente de ola como una línea a lo largo de la cresta de la ola. La ecuación para el desplazamiento asociado a una onda sinusoidal plana (de amplitud unitaria) en tres dimensiones en algún instante en el tiempo es

\[h(x, y, z)=\sin (\mathbf{k} \cdot \mathbf{x})=\sin \left(k_{x} x+k_{y} y+k_{z} z\right)\label{2.9}\]

Dado que los frentes de onda son líneas o superficies de fase constante, la ecuación que define un frente de onda es simplemente\(\mathbf{k} \cdot \mathbf{x}=\text { const. }\)

En el caso bidimensional simplemente establecemos k _z = 0. Por lo tanto, un frente de onda, o línea de fase constante 9 en dos dimensiones se define por la ecuación

\[\mathbf{k} \cdot \mathbf{x}=k_{x} x+k_{y} y=\phi \quad \text { (two dimensions). }\label{2.10}\]

Esto se puede resolver fácilmente para y para obtener la pendiente e intercepción del frente de ola en dos dimensiones.

En cuanto a las ondas unidimensionales, la evolución temporal de la onda se obtiene agregando un término - ωt a la fase de la onda. En tres dimensiones el desplazamiento de onda en función tanto del espacio como del tiempo viene dado por

\[h(x, y, z, t)=\sin \left(k_{x} x+k_{y} y+k_{z} z-\omega t\right)\label{2.11}\]

La frecuencia depende en general de los tres componentes del vector de onda. La forma de esta función,\(\omega=\omega\left(k_{x}, k_{y} k_{z}\right)\) que como en el caso unidimensional se denomina relación de dispersión, contiene información sobre el comportamiento físico de la onda.

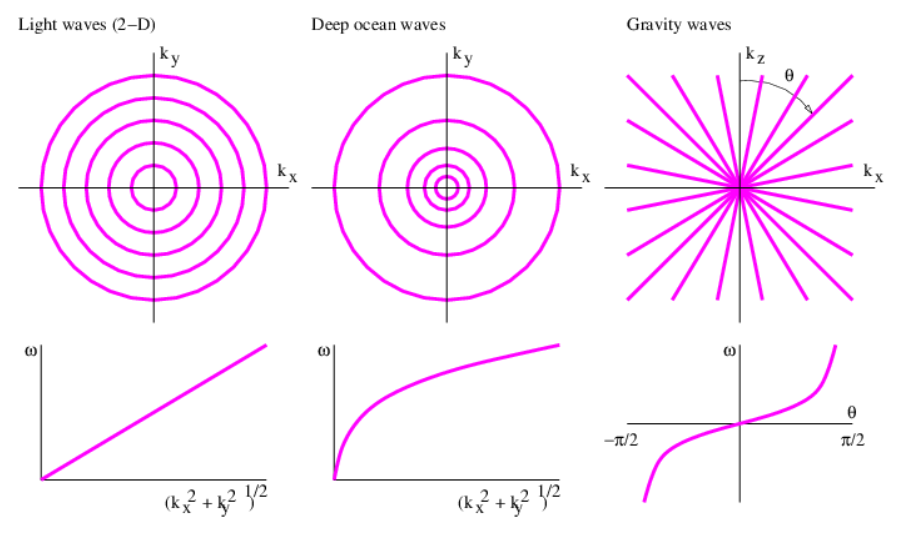
Algunos ejemplos de relaciones de dispersión para olas en dos dimensiones son los siguientes:

• Las ondas de luz en un vacío en dos dimensiones obedecen\[\omega=c\left(k_{x}^{2}+k_{y}^{2}\right)^{1 / 2}\label{2.12}\] donde c es la velocidad de la luz en un vacío.
• Las ondas oceánicas de aguas profundas en dos dimensiones obedecen\[\omega=g^{1 / 2}\left(k_{x}^{2}+k_{y}^{2}\right)^{1 / 4} \quad \text { (ocean waves) }\label{2.13}\] donde g es la fuerza del campo gravitacional de la Tierra como antes.
• Ciertos tipos de ondas atmosféricas confinadas a un plano x - z vertical llamado ondas gravitacionales (que no deben confundirse con las ondas gravitacionales de la relatividad general) obedecen\[\omega=\frac{N k_{x}}{k_{z}} \quad \text { (gravity waves), }\label{2.14}\] donde N es una constante con las dimensiones del tiempo inverso llamadas la frecuencia Brunt-Väisälä.

Las gráficas de contorno de estas relaciones de dispersión se trazan en los paneles superiores de la figura 2.6. Estas parcelas deben interpretarse como mapas topográficos, donde las líneas representan contornos de elevación constante. En el caso de la figura 2.6, se representan en su lugar valores constantes de frecuencia. Por simplicidad, los valores reales de frecuencia no están etiquetados en las gráficas de contorno, sino que se representan en las gráficas en los paneles inferiores. Esto es posible porque la frecuencia depende solo de la magnitud del vector de onda (k _x ² + k _y ²) ^{1 2} para los dos primeros ejemplos, y solo de la dirección del vector de onda θ para el tercero.

Figura\(\PageIndex{2}\): .6: Gráficas de contorno de las relaciones de dispersión para tres tipos de ondas en dos dimensiones. En los paneles superiores las curvas muestran líneas o contornos a lo largo de los cuales la frecuencia ω toma valores constantes. Los contornos se dibujan para valores igualmente espaciados de ω. Para las ondas de luz y oceánicas la frecuencia depende únicamente de la magnitud del vector de onda, mientras que para las ondas de gravedad depende únicamente de la dirección del vector de onda, definida por el ángulo θ en el panel superior derecho. Estas dependencias para cada tipo de onda se ilustran en los paneles inferiores.