11.1: Tutorial de Matemáticas — Producto Cruzado

Última actualización
Guardar como PDF

Page ID: 125995

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Hay dos formas de multiplicar dos vectores juntos, el producto punto y el producto cruzado. Ya hemos estudiado el producto punto de dos vectores, lo que da como resultado un número escalar o único.

Figura 11.1: Ilustración del producto cruzado de dos vectores A y B. El vector resultante C es perpendicular al plano definido por A y B.

El producto cruzado de dos vectores da como resultado un tercer vector, y se escribe simbólicamente de la siguiente manera:

\[\mathbf{C}=\mathbf{A} \times \mathbf{B}\label{11.1}\]

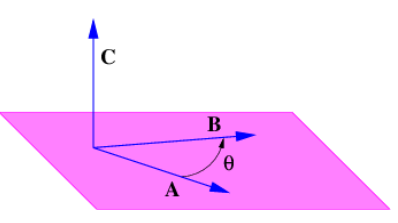
Como se ilustra en la figura 11.1, el producto cruzado de dos vectores es perpendicular al plano definido por estos vectores. Sin embargo, esto no nos dice si el vector resultante en la figura 11.1 apunta hacia arriba fuera del plano o hacia abajo. Esta ambigüedad se resuelve usando la regla de la derecha:

Apunte los dedos no curvados de tu mano derecha a lo largo de la dirección del primer vector A.
Gira tu brazo hasta que puedas curvar tus dedos en la dirección del segundo vector B.
Su pulgar estirado ahora apunta en la dirección del vector de producto cruzado C

La magnitud del producto cruzado viene dada por

\[|\mathbf{C}|=|\mathbf{A}||\mathbf{B}| \sin (\theta)\label{11.2}\]

donde | A | y | B | son las magnitudes de A y B, y θ es el ángulo entre estos dos vectores. Obsérvese que la magnitud del producto cruzado es cero cuando los vectores son paralelos o antiparalelos, y máxima cuando son perpendiculares. Esto contrasta con el producto punto, que es máximo para vectores paralelos y cero para vectores perpendiculares.

Observe que el producto cruzado no conmuta, es decir, el orden de los vectores es importante. En particular, es fácil mostrar usando la regla de la derecha que

\[\mathbf{A} \times \mathbf{B}=-\mathbf{B} \times \mathbf{A}\label{11.3}\]

Una forma alternativa de calcular el producto cruzado es más útil cuando los dos vectores se expresan en términos de componentes, es decir,\(A=\left(A_{x}, A_{y} \cdot A_{z}\right) \text { and } B=\left(B_{x}, B_{y}, B_{z}\right)\)

\ [\ comenzar {ecuación}
\ comenzar {alineado}
C_ {x} &=A_ {y} B_ {z} -A_ {z} B_ {y}\\
C_ {y} &=A_ {z} B_ {x} -A_ {x} B_ {z}\\
C_ {z} &=A_ {x} B_ {y} -A_ y {} B_ {x}
\ final {alineado}
\ final {ecuación}\ etiqueta {11.4}\]

Observe que una vez que tenga la primera de estas ecuaciones, las otras dos se pueden obtener permutando cíclicamente los índices, i. e., x → y, y → z, y z → x. Esto es útil como ayuda para la memoria.