11.2: Torsión y Momentum Angular

Figura 11.2: Una masa M localizada en r con relación al origen O tiene impulso p y tiene una fuerza F aplicada a la misma. Por la regla de la derecha el par\(\boldsymbol{\tau}=\mathbf{r} \times \mathbf{F}\) señala fuera de la página, mientras que el momento angular\(\mathbf{L}=\mathbf{r} \times \mathbf{p}\) apunta hacia la página.

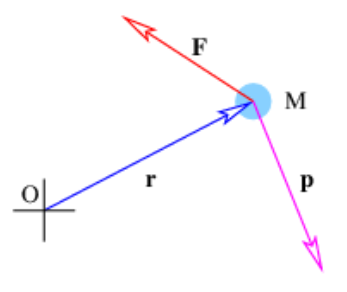
El torque es la acción de una fuerza F sobre una masa M que la induce a girar alrededor de algún punto, llamado origen. Se define

\[\tau=\mathbf{r} \times \mathbf{F}\label{11.5}\]

donde r es la posición de la masa con respecto al origen, como se ilustra en la figura 11.2.

Observe que el par es cero en varias circunstancias. Si la fuerza apunta directamente hacia o lejos del origen, el producto cruzado es cero, lo que resulta en un par cero, aunque la fuerza no sea cero. Asimismo, si r = 0, el par es cero. Por lo tanto, una fuerza que actúa en el origen no produce par. Ambos límites tienen sentido intuitivamente, ya que ninguno induce a la masa a girar en torno al origen.

El momento angular de una masa M con respecto a un punto O es

\[\mathbf{L}=\mathbf{r} \times \mathbf{p}\label{11.6}\]

donde p es el momento cinético ordinario de la masa. El momento angular es cero si el movimiento del objeto es directamente hacia o lejos del origen, o si se encuentra en el origen.

Si tomamos el producto cruzado del vector de posición y la segunda ley de Newton, obtenemos una ecuación que relaciona el par y el momento angular:

\[\mathbf{r} \times \mathbf{F}=\mathbf{r} \times \frac{d \mathbf{p}}{d t}=\frac{d}{d t}(\mathbf{r} \times \mathbf{p})-\frac{d \mathbf{r}}{d t} \times \mathbf{p}\label{11.7}\]

El segundo término en el lado derecho de la ecuación anterior es cero porque es\(d \mathbf{r} / d t\) igual a la velocidad de la masa, que es paralela a su momento y el producto cruzado de dos vectores paralelos es cero. Por lo tanto, esta ecuación puede escribirse

\[\tau=\frac{d \mathbf{L}}{d t} \quad \text { (Newton's second law for rotation). }\label{11.8}\]

Es la versión rotacional de la segunda ley de Newton.

Tanto para el par como para el momento angular la ubicación del origen es arbitraria, y generalmente se elige para la máxima comodidad. Sin embargo, es necesario elegir el mismo origen tanto para el par como para el momento angular.

Figura 11.3: Una elección conveniente de origen para un planeta (esfera derecha) que gira alrededor del sol es simplemente el centro del sol. En este caso el par de torsión de la fuerza gravitacional del sol sobre el planeta es cero.

Para el caso de una fuerza central, es decir, una que actúa a lo largo de la línea de centros entre dos objetos (como la gravedad), a menudo existe una elección de origen particularmente conveniente. Imagínese un planeta girando alrededor del sol, como se ilustra en la figura 11.3. Si el origen se coloca en el centro del sol (que se supone que no se mueve bajo la influencia de la gravedad del planeta), entonces el par ejercido sobre el planeta por la gravedad del sol es cero, lo que significa que el momento angular del planeta alrededor del centro del sol es constante en el tiempo. Ninguna otra elección de origen arrojaría este resultado conveniente.

Ya conocemos dos leyes fundamentales de conservación: las de la energía y el impulso lineal. Creemos que el momento angular se conserva de manera similar en sistemas aislados. En otras palabras, las partículas pueden intercambiar momento angular entre ellas, pero la suma vectorial del momento angular de todas las partículas en un sistema aislado de influencias externas debe permanecer constante.

Figura 11.4: Escenario para la no conservación del momento angular. F ₁₂ es la fuerza de la masa M ₂ sobre la masa M ₁ y viceversa.

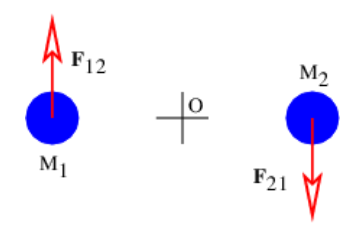
La conservación del momento angular no es una consecuencia automática de la conservación del momento lineal, aunque la ecuación gobernante (\ ref {11.8}) para el momento angular se deriva de la segunda ley de Newton. A modo de ejemplo, la figura 11.4 muestra una situación hipotética en la que la fuerza F ₂₁ de M ₁ sobre M ₂ es igual en magnitud pero opuesta en signo a la fuerza F ₁₂ de M ₂ sobre M ₁, es decir, sostiene la tercera ley de Newton, y se conserva la suma de los momentos de las dos masas. Sin embargo, debido a que las fuerzas no son centrales, el momento angular de las masas no se conserva. Este escenario es imposible si las fuerzas son centrales.