7.7: Deformación de Hielo

Como en muchos cristales, la forma en que los cristales de hielo se deforman o cizallan cuando se aplica una tensión es por propagación de dislocaciones a través del cristal. Una dislocación es un defecto de línea en un cristal que altera la disposición por lo demás ideal y regular de átomos o moléculas.

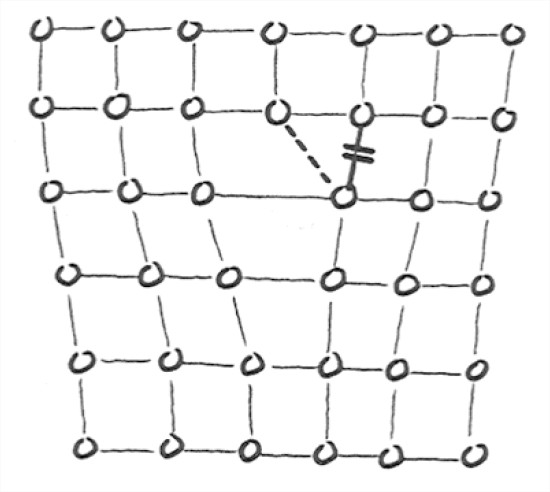
La Figura 7-20 muestra un ejemplo simple e idealizado de una dislocación. Si esquilamos este cristal, la dislocación podría migrar simplemente por rotura de enlaces y formación de nuevos enlaces. El efecto neto es mover el plano “desertado” hacia la derecha con relación a la parte inferior del cristal. La dislocación mostrada en la Figura 21 es un defecto lineal que se extiende indefinidamente en una dimensión; también hay otros tipos de dislocaciones.

El hielo se deforma principalmente por propagación de dislocaciones a lo largo del eje a (así se llama la dirección perpendicular a los hexágonos en la estructura de hielo; vea la sección sobre estructura de hielo en el Capítulo 1), así que el deslizamiento es a lo largo del plano basal (es decir, el plano perpendicular al eje a) . Aquí hay una analogía suelta pero no engañosa: piense en el hielo como un paquete de cartas orientadas a lo largo de los planos basales; son fáciles de deformar por simple cizallamiento a lo largo de estos planos. Se ha demostrado experimentalmente que no existe una dirección preferida de deslizamiento dentro del propio plano basal, y se puede demostrar teóricamente que a dentro de unos pocos grados no debería haber ninguna. Puede haber deslizamientos por dislocaciones en planos no basales, pero eso es mucho más duro —se requieren tensiones entre 10 y 20 veces más grandes— y al parecer no tiene importancia.

Figura 7-20. Ejemplo idealizado de una dislocación.

Otra forma de observar la naturaleza de la deformación del hielo es comparar su comportamiento con otros materiales en una gráfica de la tasa de deformación frente a la tensión de cizallamiento aplicada (Figura 7-21). Mencioné en el Capítulo 1 que ciertos fluidos, aire y agua incluidos, muestran una relación lineal entre la tensión de cizallamiento aplicada y la tasa de deformación por cizallamiento. Tales fluidos se llaman fluidos newtonianos. Los fluidos que muestran algún otro tipo de relación entre el estrés y la tasa de tensión se denominan fluidos no newtonianos. El hielo es uno de esos. Los materiales como el hielo son más difíciles de deformar con el aumento de la tensión, por lo que la curva de la tasa de deformación contra el esfuerzo cortante es convexa

TEMA AVANZADO: LA LEY DE FLUJO PARA EL HIELO

La relación entre la tensión aplicada y la velocidad de deformación para un continuo se denomina ley de flujo. ¿Cuál es la ley de flujo para el hielo? La ley de flujo para el hielo (tanto monocristalino como policristalino) es de la forma

tasa de deformación por cizallamiento = A (esfuerzo de cizallamiento) ⁿ (2)

donde A es un coeficiente y n es un exponente. (En el caso del agua o el aire, el exponente n es apenas 1.)

Figura 7-21. Gráfico de la tasa de deformación frente al esfuerzo cortante aplicado, mostrando el comportamiento de diversos tipos de materiales.

En cizalla simple (Figura 7-22),

\(du\)(3)

Figura 7-22. Croquis de definición para el análisis de cizallamiento simple en hielo glaciar.

La derivada du/dy, la tasa de cambio de velocidad con distancia perpendicular a los planos de cizallamiento, es lo que antes referí como la tasa de deformación por cizallamiento. (El coeficiente 2 llega ahí en virtud de la forma en que se define la tasa de deformación; no te preocupes por ello). En la Ecuación 3 el coeficiente A es como 1/viscosidad. Depende fuertemente de la temperatura. Como cabría esperar, es mucho menor (es decir, la viscosidad es mucho mayor), en dos órdenes de magnitud, para el hielo policristalino que para el hielo monocristalino orientado con el plano basal paralelo a los planos de cizallamiento. Esto se debe a que la deformación del hielo es por deslizamiento interno a lo largo de los planos basales, y en el hielo policristalino, la mayoría de los cristales no están orientados favorablemente para ello. El exponente n es difícil de medir con precisión, ¡incluso en el laboratorio! El valor generalmente citado es 3 para el hielo policristalino, pero no hay nada exacto en este valor. Y n no depende de manera importante ni de la temperatura ni de la presión.

TEMA AVANZADO: EL FLUJO DESCENDENTE DE LOS GLACIARES

Una cosa que podemos hacer a modo de teoría sobre el movimiento glaciar es considerar el equilibrio de un alcance dado o segmento fluvial del glaciar escribiendo una ecuación de fuerza-equilibrio. Esto es paralelo a la derivación de la ecuación de resistencia fundamental para ríos en el Capítulo 5.

Piense en un glaciar algo idealizado de espesor uniforme y extensión lateral infinitamente ancha que fluye por una superficie plana de roca madre (Figura 7-23). Debe haber un equilibrio entre el componente de pendiente descendente de la gravedad (la fuerza impulsora) y la fricción entre el glaciar y su lecho (la fuerza de resistencia), al igual que en el flujo constante y uniforme de agua en un canal abierto. Las aceleraciones del glaciar son muy pequeñas y pueden ignorarse para ello, aunque no son poco importantes en otros aspectos.

Figura 7-23. Croquis de definición para el equilibrio de fuerzas en una masa de hielo en un glaciar del valle, para derivar una ecuación de resistencia para el flujo glaciar.

3. Escribir el balance de fuerzas para un bloque del glaciar con ancho unitario y longitud unitaria, como se muestra en la Figura 7-23 (al igual que para el flujo de agua de canal uniforme constante; ver Capítulo 5 sobre ríos),

\(a_{\tau }= \rho gh sin\alpha\)(4)

donde τ _o es el esfuerzo cortante, ρ es la densidad del hielo, g es la aceleración de la gravedad, h es el grosor del hielo y α es el ángulo de pendiente.

Aquí hay dos formas en las que la Ecuación 4 es importante:

• Proporciona la mejor manera de estimar la tensión cortante límite de un glaciar: típicamente 0.5—1.5 bares (1 bar es aproximadamente 1 atmósfera). Nota: esto es mucho menor que la presión hidrostática en la base del glaciar.
• Esto no nos dice nada sobre las velocidades en el glaciar. Pero puede, si lo combinamos con la ley de flujo para el hielo. Consulta el siguiente desarrollo si te interesan los detalles.

Primero modifique la ecuación de resistencia, Ecuación 4, para obtener τ en función de la posición por encima del lecho (Figura 7-24):

\(\tau = \rho g(h-y)sin\alpha \)(5)

Ahora tenemos dos ecuaciones para τ:

\(\tau ^{n}= \frac{1}{2A}\frac{du}{dy}\)(6)

\( \tau ^{n}=[\rho gsin\alpha (h-y)]^{n}\)(7)

Eliminando τ de las Ecuaciones 6 y 7,

\(\frac{du}{dy}=2A[\rho g(h-y)sin\alpha ]^{n}\)(8)

Esta sencilla ecuación diferencial es fácil de resolver:

\(u = 2A (\rho gsin\alpha )n\int_{0}^{h}(h-y)^{n}dy+c\)(9)

Para evaluar la constante de integración c, utilice la condición límite que u = u _s, la velocidad superficial, a y = h. Encuentras que c = u _s. Entonces

\(u_{s}-u = \frac{1}{n+1}2A(\rho gsin\alpha )^{n}(h-y)^{n+1}\)(10)

Si u = u _b e y = 0, donde u _b es la parte de deslizamiento basal de la velocidad del glaciar, la Ecuación (10) se convierte

\(u_{s}-u_{b} = \frac{1}{n+1}2A(\rho gsin\alpha )^{n}h^{n+1}\)(11)

Usando el valor de 3 para n, las ecuaciones (10) y (11) se convierten

\(u_{s}-u = \frac{A}{2}(\rho gsin\alpha )^{3}(h-y)^{4}\)(12)

\(u_{s}-u_{b} = \frac{A}{2}(\rho gsin\alpha )^{3}h^{4}\)(13)

Figura 7-24. Croquis de definición para el equilibrio de fuerzas sobre una masa de hielo en un glaciar del valle, para derivar una distribución de velocidad a lo largo de una línea normal a la base del glaciar.

Obsérvese en las Ecuaciones 12 y 13 que, siendo iguales otras cosas, la velocidad del glaciar varía como la tercera potencia de la pendiente y la cuarta potencia del espesor.

Todo esto es para un flujo constante y uniforme, pero debido a que los glaciares tienen aceleraciones muy pequeñas, y a una primera aproximación son láminas, no está mal. Pero la temperatura tiene un efecto muy importante, a través de la variación del valor de A.

¿Cómo se compara un resultado teórico como este con las velocidades medidas? No está mal. Hasta el momento, tales comparaciones se han hecho sólo para los glaciares de los valles. (Para ello, hay que extender ligeramente el modelo para tratar con un canal no infinitamente ancho, pero eso es sencillo).