1.7: Análisis cinemático y deformación
- Page ID
- 88032
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Todo lo que hemos hecho hasta ahora en este curso ha consistido en describir el 'aquí y ahora' de la geología estructural: dónde están las estructuras y cómo se orientan en la corteza terrestre en la actualidad.
Para entender el origen de las estructuras necesitamos saber cómo cambiaron las cosas durante la formación de esas estructuras, cómo se movían las cosas. Cuando estudiamos cómo se movían las cosas a lo largo del tiempo geológico, estamos estudiando cinemática.
Los movimientos básicos

La deformación puede implicar 4 tipos de movimiento:
- Traducción o cambio de posición
- Rotación o cambio de orientación
- Dilatación o cambio de área o volumen
- Distorsión o cambio de forma.
Las dos primeras son deformaciones corporales rígidas. Los dos últimos juntos constituyen deformación o deformación no rígida.
Traducción
La traslación se mide como desplazamiento. Cualquier desplazamiento tiene una distancia y una dirección. Cuando miramos las fallas mediremos el desplazamiento de una pared de una falla con relación a otra. El desplazamiento es una cantidad vectorial.
Rotación
La rotación, o cambio de orientación, se mide típicamente en grados, alrededor de un eje de rotación particular. (Por lo tanto, una rotación es también una cantidad vectorial, porque tiene una magnitud y una dirección).
Un problema cinemático común que implica la rotación es eliminar los efectos del plegado de alguna estructura. Por ejemplo, un sedimentólogo puede medir la orientación de una estructura paleocurrent en estratos plegados, y quiere conocer la dirección original del flujo de corriente.
Este tipo de problema se resuelve más fácilmente en la proyección estereográfica. A medida que los lechos se 'despliegan', las direcciones paleocurrent que contienen giran a lo largo de pequeños círculos en la estereoneta. Los pequeños círculos están centrados en el eje de plegado.
Dilatación
El cambio de volumen es muy difícil de medir en rocas reales. No obstante, en algunas circunstancias se puede cuantificar. La mayoría de las rocas sedimentarias sufren cierta compactación ya que son enterradas, debido a que se expulsa el agua porosa La compactación da como resultado una dilatación negativa. Otro fenómeno común que implica dilatación negativa es la solución de presión en la que algunos minerales en una roca se disuelven en respuesta al estrés.
La dilatación es una cantidad escalar — solo tiene una magnitud.
Distorsión
La distorsión es, con mucho, el tipo de deformación más complicado de medir. Cuando las rocas están distorsionadas suelen alargarse en algunas direcciones y más cortas en otras. Además, los ángulos cambian en la distorsión. Debido a esto, la cepa no puede ser representada por un escalar o un vector. Es una cantidad más complicada que se llama tensor.
Cepa
En el discurso popular la palabra “tensión” evoca una impresión de aplicar fuerza; “esforzarse” en algo implica un proceso dinámico. La palabra “cepa” tiene un significado diferente en la ciencia y la ingeniería —describe algo puramente cinemático— un cambio en la forma o el volumen, sea cual sea su origen. Hay ejemplos de tensión en los que no hay fuerza involucrada: Un reflejo en un espejo distorsionado, y la imagen distorsionada de una pelota de baloncesto en un televisor de pantalla ancha son ambas imágenes que han sufrido tensión, pero están hechas de rayos de luz; ninguna fuerza está causando la distorsión.
(El término dinámico correspondiente es “estrés”, que estudiaremos en una sección posterior. ¡Tenga cuidado de no confundir el estrés con la tensión!)
Todas las estructuras que vemos en la corteza terrestre son manifestaciones de tensión. La cepa es un concepto tan fundamental en geología estructural que en cursos más avanzados, las matemáticas de la cepa a menudo se tratan primero. En este curso tomamos un enfoque más práctico y nos enfocamos en describir primero las estructuras. No obstante, a estas alturas, debería quedar claro que los cambios en la forma de las rocas pueden reconocerse en todas las estructuras que has estudiado hasta el momento.
Cepa heterogénea y cepa homogénea
La tensión puede variar de un lugar a otro en las rocas. Distinguimos un caso especial:
Cepa homogénea: cepa que es la misma en todas partes dentro de un cuerpo de roca. En deformación homogénea, las líneas rectas permanecen rectas, las líneas paralelas permanecen paralelas, los círculos se deforman en elipses.
La cepa que no es homogénea es heterogénea. En la deformación heterogénea, las líneas rectas se pueden doblar, y las líneas que inicialmente eran paralelas se rotan en diferentes cantidades, volviéndose no paralelas.
La cepa heterogénea es difícil de tratar matemáticamente. Sin embargo, si observamos una región muy pequeña de una roca heterogéneamente tensa, a menudo se puede tratar de la misma manera que una cepa homogénea. La deformación en un punto en una roca heterogéneamente tensada sigue las mismas reglas matemáticas que la deformación homogénea.


Colar en líneas
Incluso en una cepa homogénea, las líneas orientadas de manera diferente experimentan diferentes cantidades de tensión. En el diagrama, cada trilobite se ve afectado de manera diferente por la deformación, a pesar de que la deformación general es homogénea.
Cambios en la longitud (deformación longitudinal)

Hay dos formas de medir el cambio en la longitud. Si la longitud original es l 0 y la nueva longitud es l,
Extensión (a veces elongación) e = (l-l 0) /l 0
La extensión es el cambio fraccionario de longitud.
Estiramiento s = l/l 0 = 1+e
Lo importante a recordar es que en las rocas tensas el alargamiento varía con la dirección: normalmente algunas líneas se habrán alargado y otras se habrán acortado.
Cambios en los ángulos (deformación por cizallamiento)

Para medir el cambio en los ángulos observamos dos líneas que originalmente eran perpendiculares.
Si el cambio en el ángulo es ψ (psi) entonces
Deformación cortante (gamma) γ= tan ψ
Existen otros métodos utilizados para medir la deformación por cizallamiento en estudios avanzados, por lo que la definición anterior a veces se califica como deformación por cizallamiento de ingeniería porque es la medida supuestamente más utilizada por los ingenieros.
La deformación por cizallamiento también varía con la dirección: algunas líneas experimentan deformación por cizallamiento positiva y otras sufren deformación por cizallamiento negativa.
En el diagrama, el eje largo del trilobite ha sufrido una deformación positiva por cizallamiento debido a que la línea originalmente perpendicular a él ha girado relativamente en sentido horario.
Elipse de deformación
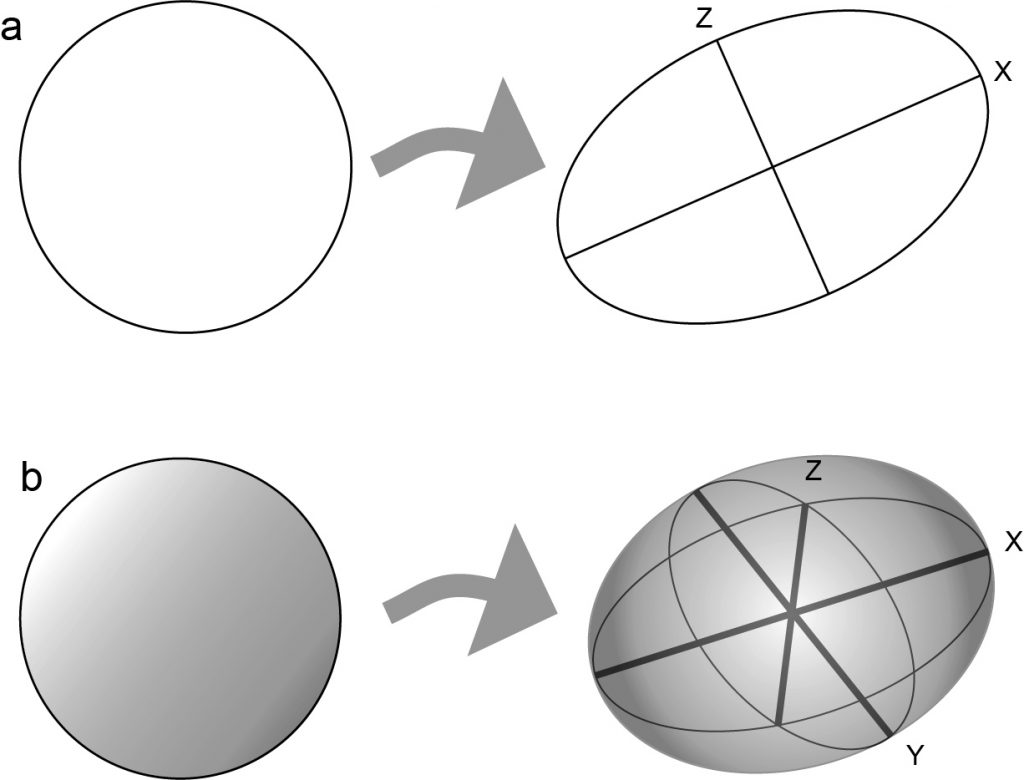
La elipse de deformación es una manera conveniente de representar un estado de deformación homogénea, o la deformación en un punto, en una superficie bidimensional. La elipse de deformación es la forma de un círculo deformado que originalmente tenía radio unitario.
El radio de la elipse de deformación en cualquier dirección es igual al tramo s en esa dirección. Por lo tanto, la elipse de deformación es una buena manera de representar la variación de la deformación longitudinal con la dirección.
Ejes de deformación
Una elipse de deformación tiene dos líneas que son especiales. Representan los tramos máximo y mínimo. Estas líneas son ejes de deformación. (Los ejes de deformación a veces se llaman X y Z. (Nota: los ejes de coordenadas en un mapa o sección transversal son a veces x y z. Los ejes de deformación no necesariamente coinciden con ninguna dirección especial en un mapa).
Los ejes de deformación tienen algunas otras propiedades especiales. Siempre están en ángulo recto entre sí, y también representan líneas de deformación por cizallamiento cero. Esto significa que también eran perpendiculares antes de que comenzara la deformación. (Sin embargo, durante la deformación pueden haber divergido de esta relación perpendicular y luego volver a ella!). Los ejes de deformación son las únicas líneas que tienen esta propiedad.
La relación de deformación es una medida conveniente de la cantidad de distorsión en 2-D. La relación de deformación es la relación entre el eje largo y el eje corto de la elipse de deformación:
Relación de deformación R S = s X /s Z
Elipsoide de deformación
El elipsoide de deformación es una manera conveniente de representar un estado de deformación homogénea, o la deformación en un punto, en tres dimensiones. El elipsoide de deformación es la forma de una esfera deformada que originalmente tenía radio unitario.
El radio del elipsoide de deformación en cualquier dirección es igual al tramo s en esa dirección. En 3-D, el elipsoide de deformación es así una buena manera de representar la variación de la deformación longitudinal con la dirección.
Un elipsoide de deformación tiene tres líneas X, Y y Z que son especiales. Representan los tramos máximo y mínimo, denominados s X y s Z respectivamente, y un tercer eje intermedio del tramo intermedio s Y, que es mutuamente perpendicular a los otros dos. Estas líneas son ejes de deformación.
Tienen algunas otras propiedades especiales. Están en ángulo recto entre sí, y también representan polos a planos de deformación por cizallamiento cero. Esto significa que también eran perpendiculares antes de que comenzara la deformación. (Sin embargo, durante la deformación pueden haber divergido de esta relación perpendicular y luego volver a ella!). Los ejes de deformación son las únicas líneas que tienen esta propiedad.
En 3D los ejes de deformación son polos a tres planos principales de deformación.
En 3D la forma del elipsoide de deformación no se puede definir por una sola relación de deformación. En su lugar se reconocen dos relaciones de deformación a= s X/s Y y b= s Y/s Z. Si a es grande y b es pequeño entonces la cepa elipsoide se ve como una pelota de fútbol o un cigarro, y se describe como prolada. Las rocas con cepas proladas suelen mostrar fuertes telas lineales (lineaciones). En contraste si a es pequeño y b es grande entonces el elipsoide cepa parece un cojín o un panqueque, y se describe como oblato. Las rocas con cepas oblatas suelen mostrar telas planas fuertes (foliaciones).

El rango de posibles formas elipsoides de deformación se puede ilustrar en una gráfica de a contra b conocida como gráfica de Flinn.

Historias de deformaciones
Deformación rotacional y no rotacional
Todas las medidas anteriores se han referido solo a la tensión. Sin embargo, si observamos toda la imagen de deformación, podemos ver situaciones en las que la rotación ha pasado al mismo tiempo que la tensión. En estas circunstancias es útil observar el comportamiento de los ejes de deformación.
Si los ejes de deformación tienen la misma orientación que antes de que comenzara la deformación, entonces la deformación es no rotacional (a veces irrotacional). (Tenga en cuenta que incluso en una deformación no rotacional otras líneas se habrán girado, y mostrarán deformación por cizallamiento, pero son los ejes de deformación los que son importantes para la terminología aquí).
Si los ejes de deformación han girado durante la deformación, entonces la deformación se describe como rotacional.
Deformación finita y tasa de deformación
Una vez que comenzamos a mirar la rotación, también es difícil evitar discutir el historial de tensiones. Cuando miramos una roca deformada lo que vemos es producto de toda una historia de deformación. Ese producto final se llama deformación finita y la parte de deformación de deformación es la deformación finita.
En análisis más detallados de la cepa, podemos estar interesados en todos los pequeños incrementos de cepa que han contribuido a la imagen final. Cada uno se llama cepa incremental.
La cepa infinitesimal es el producto final de este tipo de pensamiento. Se piensa que el historial de cepas está compuesto por un número infinito de incrementos infinitesimales de deformación. (La idea general debería ser familiar si has tomado una clase de cálculo). Esta idea de cepa infinitesimal se vuelve importante si observamos las tasas de deformación. Las tasas de deformación se miden típicamente en unidades de por segundo, o s -1 a veces se expresan como cepas por segundo. En situaciones geológicamente razonables, la cantidad de tensión que ocurre en un segundo es casi infinitesimal. Se cree que las tasas de deformación dúctil típicas en la corteza terrestre están entre 10 -12 y 10 -15 s -1.
Historias de deformaciones coaxiales y no coaxiales
Si los incrementos de deformación no son rotacionales, entonces los ejes de deformación mantienen su misma dirección en relación con el material de la roca. La deformación se llama coaxial. Este tipo de deformación también se llama deformación pura.

Cualquier otro tipo de historia de cepa es un no coaxial. Hay muchos tipos de historia de deformación no coaxial, pero un tipo particular es importante en el estudio de las zonas de cizallamiento. Es simple cizalla. En cizallamiento simple, todas las partículas de la roca se mueven en la misma dirección, pero los ejes de deformación se giran progresivamente. A veces, al observar en detalle el tejido de las zonas de corte, podemos distinguir el sentido de rotación y averiguar en qué dirección se movían las rocas.


