2.3: Laboratorio 3 - Trabajar con Proyecciones Estereográficas

Operaciones básicas de trazado

Configuración de la proyección

Necesitarás una red Wullf. Puedes descargar uno aquí: WULFF NET 15 cm.

Para su uso en este curso, su red debe tener 15 cm de diámetro. Si descargas la tuya propia, imprime la red Wullf en una hoja de papel normal a escala 100%. (Muchas computadoras encogerán automáticamente la imagen para que se ajuste a un área de papel más pequeña por defecto. Utilice las opciones en el cuadro de diálogo de la impresora en su computadora para imprimir al 100%.)

A continuación, use una tachuelas anticuadas para el pulgar para hacer un pequeño agujero a través del centro exacto de la red. Después inserte la tachuela apuntando hacia arriba, a través del agujero.

Ahora, toma una hoja de papel de calco y presiónala sobre la red para que la tachuela haga un agujero limpio en el centro.

Después, traza el contorno circular, el borde de la red, conocido como el primitivo, en el papel de calco. Marcar los cuatro puntos cardinales N, E, S, W, en el papel de calco ^[1] con pequeñas 'garrapatas', y distinguir N con una flecha.

Ahora debería poder rotar su proyección (en el papel de calco) sobre la red, y luego devolverla a la posición inicial con N en la parte superior.

Trazar la orientación de una línea

La información geométrica más simple que se puede mostrar en una proyección estereográfica es la orientación de una línea vertical. Se proyecta como un punto en medio de la estereoneta. La siguiente información más fácil de retratar es la orientación de una línea que tiene una tendencia hacia el norte o hacia el sur. Con la superposición en la posición de referencia, cuente la cantidad de caída desde la marca de índice norte o sur (según corresponda) en la primitiva hacia el centro de la red a lo largo de la línea N-S, y coloque un punto en el papel de calco en esta posición. Recuerde, una línea está representada por un punto en el estereograma.

El procedimiento para una línea de orientación general es el siguiente:

a) Visualizar primero el problema, usando un lápiz. Imagínese que el lápiz se origina en el centro de la red, y se extiende hacia abajo para intersectar un “cuenco” debajo de la red. ¿En qué cuadrante se cruzará el hemisferio, y si estará cerca de lo primitivo o lejano?

b) Con la superposición en la posición de referencia, hacer una marca en la primitiva que corresponda a la tendencia de la línea.

c) Gire la superposición hasta que la marca esté alineada con un radio recto de la red; cuente el ángulo de caída hacia adentro desde la primitiva a lo largo del radio recto, y haga una pequeña cruz.

d) Devolver la superposición a la posición de referencia y verificar que la cruz esté en la posición general esperada.

Figura 1. Procedimiento para trazar la proyección estereográfica de una línea hundida. Inmersión de 38 y tendencia de 222. Papel calco mostrado gris.

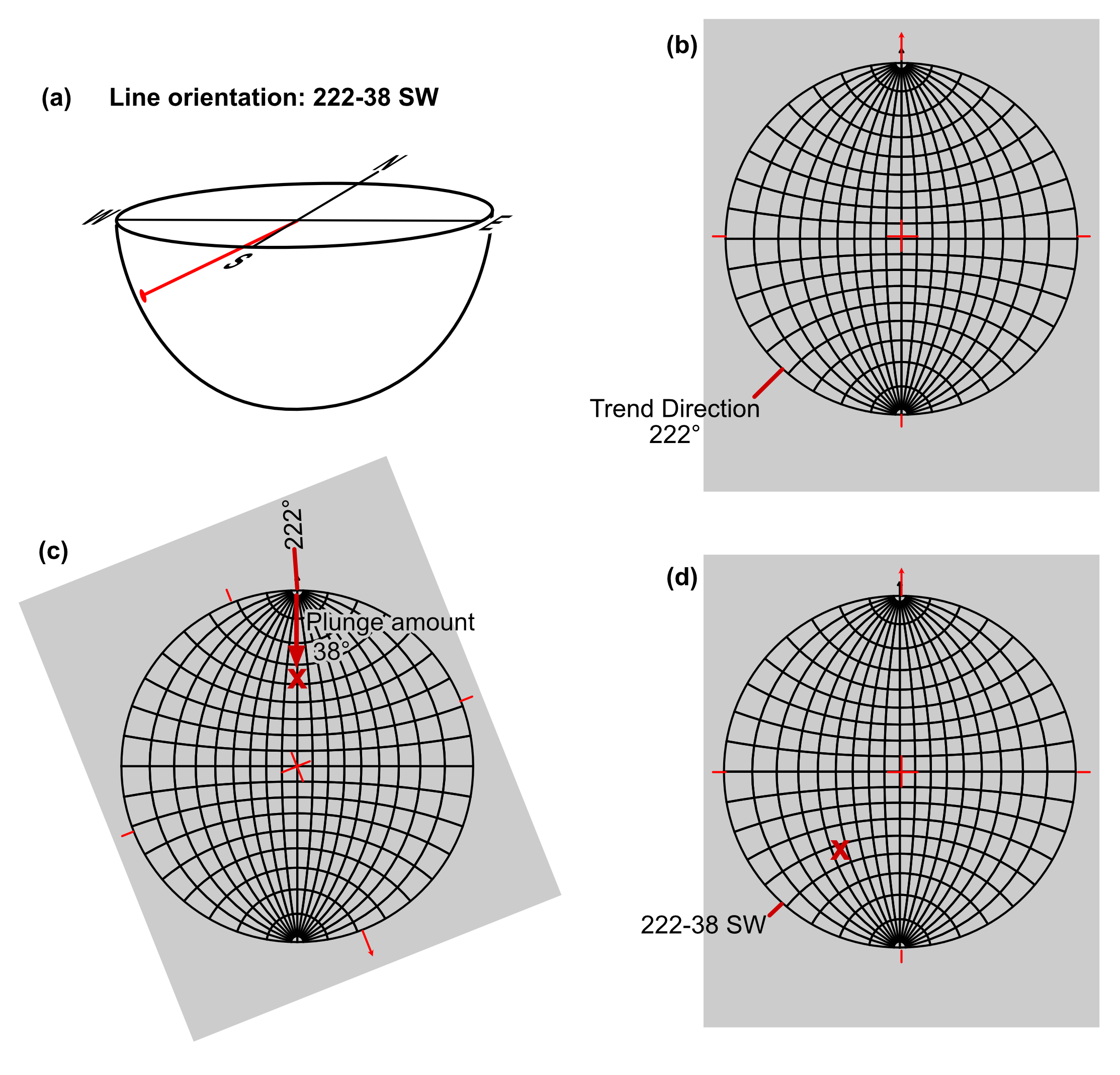
Problema de ejemplo: Trazar el punto L que representa la línea 300-50. En tu proyección etiqueta los ángulos correspondientes a la tendencia y zambullida.

Trazando un plano y su polo

Los planos horizontales y verticales son sencillos de trazar. Un plano horizontal está representado por lo primitivo. Los planos verticales de impacto N-S y E-W están representados por las líneas rectas en la estereoneta que conectan los polos N-S y las posiciones E-W, respectivamente. Otros planos verticales son diámetros rectos orientados paralelos al golpe.

Para trazar un plano inclinado siga estos pasos:

a) Visualiza el problema usando tu mano o un trozo de papel. Imagínese que este objeto plano pasa por el centro de la parcela e intersecta un hemisferio debajo de la red. ¿En qué cuadrantes se ubicará la línea curva de intersección y qué tan cerca de la primitiva estará esa curva? ¿Dónde estará su polo? El poste debe estar en el lado opuesto de la red. Si el gran círculo está cerca de lo primitivo entonces el polo estará cerca del centro, y viceversa.

b) Con la superposición en la posición de referencia hacer una marca en la primitiva que corresponda a la dirección de impacto del plano. Como cuestión de práctica sonora, siempre debes hacer esta marca en la dirección del golpe de acuerdo con la regla de la mano derecha.

c) Gire la estereoneta hasta que la marca quede alineada con el punto superior de la red. Desde el lado derecho de la red, cuente grados hacia adentro a lo largo del radio recto, hasta llegar a la cantidad de inmersión. Trazar el gran círculo que pasa por este punto; opcionalmente, para trazar el polo al plano, contar el mismo número de grados hacia afuera desde el centro a lo largo del radio recto hacia el lado izquierdo de la red y marcar una pequeña 'x'.

d) Devolver la superposición a la posición de referencia y verificar que el gran círculo corresponda con la orientación anticipada.

Figura 2. Procedimiento para trazar la proyección estereográfica de un plano inclinado con un golpe de 100, una caída de 40, y el polo al plano. Papel calco mostrado gris.

Problema de ejemplo: Construir el gran círculo que representa el plano 120/50, y su polo. En la etiqueta de proyección los ángulos correspondientes a la dirección de impacto, inmersión y inmersión numérica del plano.

Trazar una línea en un plano por rastrillo o paso

Una línea que se encuentra en un plano se traza como un punto en un gran círculo.

a) Trazar el plano como un gran círculo siguiendo los pasos a-c del procedimiento anterior.

b) Desde el punto superior de la red, cuente grados a lo largo del gran círculo que acaba de trazar hasta alcanzar el ángulo de rastrillo deseado.

Medir la orientación de una línea desde su polo

Encontrar la orientación de una línea desde su polo es solo lo contrario del procedimiento de trazado anterior.

a) Gire la red para colocar el poste en cualquiera de los cuatro radios rectos. Marcar un punto en la primitiva al final de este radio recto.

b) Cuenta grados de hundimiento hacia adentro desde lo primitivo hasta llegar al polo. Graba la caída.

c) Devolver la red a la posición de referencia. Contar grados en el sentido de las agujas del reloj alrededor de la primitiva hasta llegar a la marca hecha en el paso a. esta es la tendencia.

Problema de ejemplo: ¡mide la orientación de la línea que trazaste en el primer ejemplo y mira si obtienes la respuesta con la que empezaste!

Midiendo el golpe y la caída de un avión desde su gran círculo

Medir el golpe y la caída representados por un gran círculo es solo lo contrario del procedimiento de trazado para un plano.

a) Gire la red hasta que el plano esté en un gran círculo en la mitad derecha de la red. (Esto asegura una respuesta consistente con la regla de la derecha).

b) Marcar el final del gran círculo que está en la parte superior de la red.

c) Contar grados de inmersión hacia adentro desde el lado derecho a lo largo del radio recto hasta llegar al gran círculo.

d) Regresar a la posición de referencia y anotar el acimut de la marca realizada en el paso b. Este es el strike.

Medir el golpe y la caída de un avión desde su polo

Un polo es perpendicular al plano que representa, así que los pasos a y c se hacen de una manera que parece opuesta al procedimiento cuando se trabaja con un gran círculo, ¡o traza!

a) Gire la red hasta que el poste esté en el radio recto del lado izquierdo de la red.

b) Marcar el final del gran círculo que está en la parte superior de la red.

c) Contar grados de inmersión hacia afuera desde el centro a lo largo del radio recto hacia el lado izquierdo de la red hasta llegar al poste.

d) Regresar a la posición de referencia y anotar el acimut de la marca hecha en b. Este es el strike.

Problema de ejemplo: mide la orientación del plano que trazaste en el primer ejemplo trabajando hacia atrás desde su poste y ¡mira si obtienes la respuesta con la que empezaste!

Construcciones sobre la proyección estereográfica

Figura 3. Cálculos que involucran líneas.

Encontrar el plano común a dos líneas

Si tiene dos líneas trazadas como puntos en la proyección estereográfica, el plano común a las dos líneas se traza como un gran círculo que pasa por ambos puntos.

a) Trazar ambas líneas como puntos.

b) Gire la red para que ambos polos se encuentren en un solo gran círculo.

c) Trazar el gran círculo que representa el plano.

Encontrar la línea perpendicular a otras dos líneas

Para cualquiera de dos líneas orientadas de manera diferente, habrá una tercera línea que es perpendicular a ambas.

a-c) Repita los pasos a-c anteriores.

d) Encontrar el polo al plano; representa la línea perpendicular.

Ángulo entre dos líneas

Es posible medir el ángulo entre las dos líneas contando cuadrados de 2 grados a lo largo del gran círculo que pasa por ambas.

a-b) Repita los pasos a-b anteriores.

c) Contar grados a lo largo del gran círculo entre las dos líneas.

Tenga en cuenta que, a menos que las líneas estén a 90°, siempre habrá dos respuestas: una mayor que 90° y otra menor que 90°.

Problema de ejemplo: Construir el plano común a las líneas 318-34 y 206-78; determinar el ángulo entre ellas; también determinar el golpe y la caída del plano común.

Figura 4. Cálculos que involucran planos.

Línea de intersección de dos planos

La línea de intersección de dos planos está representada por el punto donde se cruzan sus grandes círculos.

a) Trazar los dos planos que se cruzan como grandes círculos sobre la superposición.

b) Los grandes círculos se cruzan en un punto de la superposición, lo que representa una línea de intersección de los dos planos. Determinar la orientación de la línea.

Plano perpendicular a dos planos

Para encontrar el plano perpendicular a otros dos planos, primero encontramos su línea de intersección, y luego la usamos como polo a un tercer plano.

a) Repita el paso a anterior

b) Repita el paso b anterior, pero en lugar de determinar la tendencia y la caída, mueva el punto de intersección al radio recto del lado izquierdo de la red.

c) Contar el número de grados hacia afuera desde el centro de la red, a lo largo del radio recto izquierdo hasta este punto.

d) Contar el mismo número de grados hacia adentro desde la primitiva a lo largo del radio recto derecho, y trazar el gran círculo que pasa por este punto.

Ángulo entre dos planos

Existen varios métodos para encontrar el ángulo entre un par de planos. Es posible medir el ángulo entre los dos grandes círculos con un traslador, pero esto no es muy preciso. Se recomiendan dos métodos. El primer método es más fácil de visualizar, pero el segundo método es más rápido. Usa lo que prefieras.

Primer método

a-d) Encuentra el gran círculo perpendicular a los dos planos como arriba.

e) Localizar el punto donde cada plano original se cruza con el nuevo gran círculo.

f) Contar el número de grados a lo largo del nuevo gran círculo entre estos puntos.

Segundo método

a) Trazar ambos planos como polos.

b) Gire la red para que ambos polos se encuentren en un solo gran círculo.

c) Contar grados entre los dos polos.

Nota importante: siempre hay dos posibles respuestas al ángulo entre dos planos. Los dos ángulos sumarán hasta 180°. ¡La única manera de averiguar cuál es la respuesta correcta a un problema geológico dado es visualizar el problema en 3D!

Problema de ejemplo: Trazar la línea de intersección de los planos 132/22 y 074/68. También trazar un tercer plano perpendicular a ambos, y encontrar el ángulo entre los dos planos. Determinar la orientación de la línea de intersección de los dos primeros planos. Determinar la orientación del plano perpendicular.

Respuestas a los problemas del ejemplo

Las parcelas anteriores representan las respuestas a los siguientes problemas:

1) Trazar el punto L que representa la línea 300-50. En tu proyección etiqueta los ángulos correspondientes a la tendencia y zambullida.

2) Construir el gran círculo que representa el plano 120/50, y su polo. En la etiqueta de proyección los ángulos correspondientes a la dirección de impacto, inmersión y inmersión numérica del plano.

3) Trazar la línea de intersección de los planos 132/22 y 074/68. También trazar un tercer plano perpendicular a ambos, y encontrar el ángulo entre los dos planos. Determinar la orientación de la línea de intersección de los dos primeros planos. Determinar la orientación del plano perpendicular.

4) Construir el plano común a las líneas 318-34 y 206-78; determinar el ángulo entre ellas; también determinar el golpe y la caída del plano común.

Asignación

1. *Trazar y etiquetar la posición de las siguientes lineaciones en una proyección estereográfica:

a) 020-50, b) 295-10, c) 110-80, d) 170-00, e) 210-90.

2. *En una hoja separada de papel de calco trazar y etiquetar la posición de los siguientes planos inclinados y sus polos:

a) 310/40, b) 025/85, c) 134/04, d) 265/00, e) 130/90.

3. *Se establece una losa de roca en el laboratorio. Muestra una lineación y una foliación.

a) Medir el golpe y la caída de la foliación, y la caída y tendencia de la lineación con brúpas/clinómetro.

(b) Pon a prueba tu precisión trazando ambos en una proyección estereográfica. Primero, trazar la foliación como un gran círculo sobre una proyección estereográfica. A continuación, trazar como punto la zambullida y tendencia de la lineación. Si tu linación se encuentra exactamente en el gran círculo, ¡tu medición es excelente! Lo más probable es que se caiga un poco, reflejando la dificultad de medir con total precisión.

c) Medir el rastrillo de la linación con un traslador. Ahora trazar la medida del rastrillo, como un punto que se encuentra exactamente en el gran círculo. Mida el ángulo entre las dos medidas de la lineación. Esto es una indicación de la precisión de sus mediciones.

d) Usa el resultado para calificar el uso de tu brújula. (Sea honesto, ¡se trata de evaluar tu propia precisión correctamente, no la medición inicial!)

Clasificación de errores

<2° Maestro del clinómetro

2-5° Bueno

5°-10° Satisfactorio

10°-20° Podría usar más práctica

> 20° Probablemente lo mejor para volver a intentarlo

4. A lo largo de un corte vertical de ferrocarril, una bancada muestra una caída aparente de 20° en una dirección 298°. En terreno nivelado fuera del corte un geólogo puede medir el golpe de las camas como 067, pero no puede decir en qué dirección están sumergiendo. Utilice la proyección estereográfica para determinar el verdadero golpe de regla de la mano derecha y el hundimiento de la cama.

5. En Ashman Ridge en Columbia Británica, dos geólogos midieron la distancia desde la parte inferior hasta la parte superior de la Formación Quock como 205 m. La cinta métrica tenía una tendencia de 187° y una caída de 20°. Si el golpe y la caída de la Formación Quock fue 247/63 N, calcule el grosor verdadero de la formación.

6. El mapa en el que trabajaste la semana pasada contiene una veta de oro cortada por una inconformidad. Determinar la orientación del subcultivo de la vena, por proyección estereográfica.

(a) Trazar la orientación de la veta de oro como un gran círculo. Trazar la inconformidad como un segundo gran círculo. Estos valores (del laboratorio de la semana pasada) te serán dados por tus instructores.

b) Marcar el punto donde se cruzan los dos grandes círculos. Esto representa la orientación de la línea de subcultivo. Determinar la tendencia y caída de esta línea.

(c) * ¿Está de acuerdo con la respuesta que obtuvo la semana pasada por contornear?

d) Determinar el ángulo entre la vena y la discordancia.

Datos del laboratorio anterior

Copia de Lab 2 Mapa 1

Orientación de la disconformidad: _______________

Orientación de la vena:_____________________

Orientación de la línea de subcultivo:________________

RED WULFF 15 cm

---

1. A veces verá redes que han sido etiquetadas con N, S, E y W. No recomendamos esto, ya que la red se gira, durante el uso, en una variedad de orientaciones que no son N-S. Cuando es necesario, nos referimos a los puntos cardinales de la red como 'arriba', 'izquierda, 'abajo' y 'derecha'.