9.4: Isostasia
- Page ID
- 88138
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La teoría sostiene que el manto es capaz de convección por su plasticidad, y esta plasticidad también permite otro proceso muy importante de la Tierra conocido como isostasia. El significado literal de la palabra isostasia es “paralización igual”, pero la importancia detrás de ella es el principio de que la corteza terrestre flota en el manto, como una balsa flotando en el agua, en lugar de descansar sobre el manto como una balsa sentada en el suelo.
La relación entre la corteza y el manto se ilustra en la Figura\(\PageIndex{1}\) A la derecha se muestra un ejemplo de una relación no isostática entre una balsa y concreto sólido. Es posible cargar la balsa con mucha gente, y aún así no se hundirá en el concreto. A la izquierda, la relación es isostática entre dos balsas diferentes y una piscina llena de mantequilla de maní. Con una sola persona a bordo, la balsa flota alta en la mantequilla de maní, pero con tres personas, se hunde peligrosamente bajo. Estamos usando mantequilla de maní aquí, en lugar de agua, porque su viscosidad representa más estrechamente la relación entre la corteza y el manto. A pesar de que tiene aproximadamente la misma densidad que el agua, la mantequilla de maní es mucho más viscosa (rígida), y así aunque la balsa de tres personas se hundirá en la mantequilla de maní, lo hará con bastante lentitud.

La relación de la corteza terrestre con el manto es similar a la relación de las balsas con la mantequilla de maní. La balsa con una persona en ella flota cómodamente alto. Incluso con tres personas en ella la balsa es menos densa que la mantequilla de maní, por lo que flota, pero flota incómodamente baja para esas tres personas. La corteza, con una densidad promedio de alrededor de 2.6 gramos por centímetro cúbico (g/cm 3), es menos densa que el manto (densidad promedio de aproximadamente 3.4 g/cm 3 cerca de la superficie, pero más que eso a profundidad), y así está flotando sobre el manto “plástico”. Cuando se agrega más peso a la corteza, a través del proceso de construcción de la montaña, lentamente se hunde más profundamente en el manto y el material del manto que estaba allí se deja a un lado (Figura\(\PageIndex{2}\), izquierda). Cuando ese peso es eliminado por la erosión a lo largo de decenas de millones de años, la corteza rebota y la roca del manto fluye hacia atrás (Figura\(\PageIndex{2}\), derecha).

La corteza y el manto responden de manera similar a la glaciación y desglaciación como lo hacen al crecimiento y erosión de las cadenas montañosas. Gruesas acumulaciones de hielo glacial agregan peso a la corteza, y a medida que el manto debajo se aprieta hacia los lados, la corteza disminuye. Este proceso se ilustra para la actual capa de hielo en Groenlandia en la Figura\(\PageIndex{3}\) (a y b). La capa de hielo de Groenlandia en este lugar tiene más de 2,500 metros de espesor, y la corteza debajo de la parte más gruesa ha sido deprimida hasta el punto en que se encuentra bajo el nivel del mar sobre una amplia área. Cuando el hielo finalmente se derrite, la corteza y el manto rebotarán lentamente, pero el rebote completo probablemente tomará más de 10,000 años (Figura\(\PageIndex{3}\) c).


¿Cómo puede el manto ser sólido y plástico?

Quizás se estén preguntando cómo es posible que el manto de la Tierra sea lo suficientemente rígido como para romperse durante un terremoto, y sin embargo, convecta y fluye como un líquido muy viscoso. La explicación es que el manto se comporta como un fluido no newtoniano, lo que significa que responde de manera diferente a las tensiones dependiendo de la rapidez con la que se aplique el estrés. Un buen ejemplo de esto es el comportamiento del material conocido como Silly Putty, que puede rebotar y se romperá si lo tiras bruscamente, pero se deformará como un líquido si se aplica tensión lentamente. En esta foto, Silly Putty se colocó sobre un agujero en una mesa de vidrio, y en respuesta a la gravedad, fluyó lentamente hacia el agujero. El manto fluirá cuando se coloque bajo la tensión lenta pero constante de una capa de hielo en crecimiento (o derretimiento).
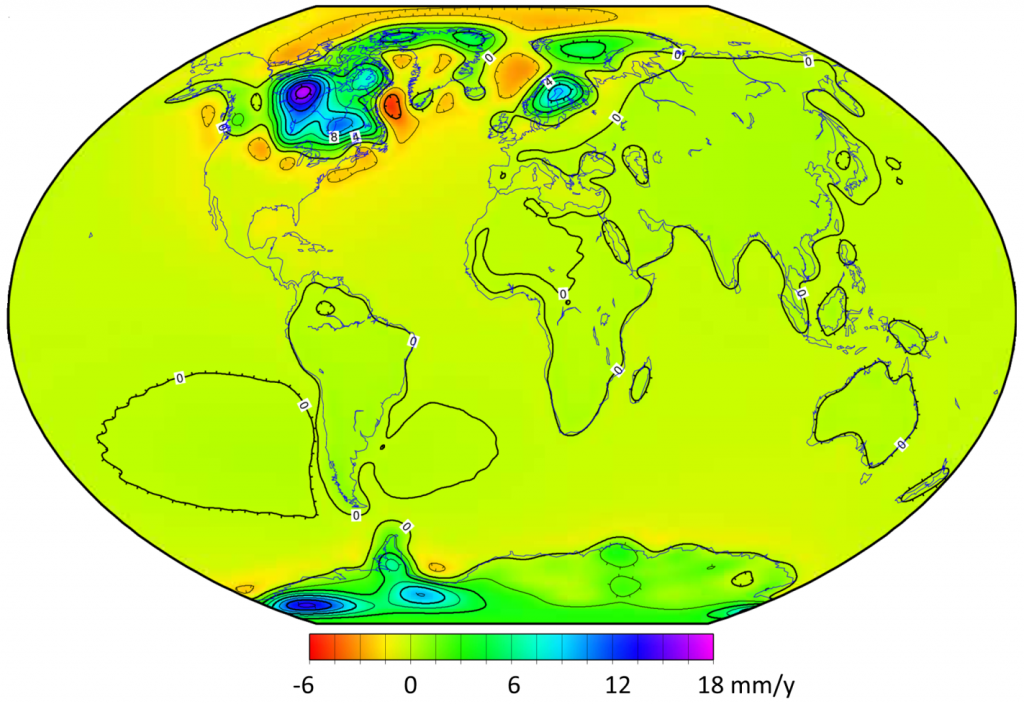
Grandes partes de Canadá siguen rebotando como resultado de la pérdida de hielo glacial en los últimos 12 ka, y como se muestra en la Figura\(\PageIndex{5}\), otras partes del mundo también están experimentando rebote isostático. La tasa más alta de elevación se encuentra dentro de una gran área al oeste de la Bahía de Hudson, que es donde la capa de hielo Laurentide fue la más gruesa (más de 3,000 m). El hielo finalmente salió de esta región hace unos 8 mil años, y actualmente la corteza rebota a un ritmo de casi 2 centímetros al año. También se está produciendo un fuerte rebote isostático en el norte de Europa, donde la capa de hielo fennoescandiana era más gruesa, y en la parte oriental de la Antártida, que también experimentó importantes pérdidas de hielo durante el Holoceno.
También hay extensas áreas de hundimiento que rodean las antiguas Láminas de Hielo Laurentide y Fenno-Scandian. Durante la glaciación, la roca del manto fluyó lejos de las áreas debajo de las capas de hielo principales, y este material ahora fluye lentamente hacia atrás, como se ilustra en la Figura\(\PageIndex{3}\) b.
Las densidades (también conocidas como “gravedad específica”) de una serie de minerales comunes se dan en el Cuadro 9.1.
| Mineral | Densidad (gramos por centímetro cúbico, g/cm 3) |
|---|---|
| Cuarzo | 2.65 |
| Feldespato | 2.63 |
| Amphibole | 3.25 |
| Piroxeno | 3.4 |
| Olivine | 3.3 |
La siguiente tabla proporciona las proporciones aproximadas de estos minerales en la corteza continental (tipificada por el granito), la corteza oceánica (principalmente basalto) y el manto (principalmente la roca conocida como peridotita). Suponiendo que tiene 1,000 cm 3 de cada tipo de roca, estime las respectivas densidades de tipo roca. Para cada tipo de roca, necesitará multiplicar el volumen de los diferentes minerales en la roca por su densidad, y luego agregar esos números para obtener el peso total de 1,000 cm 3 de esa roca. La densidad es ese número dividido por 1,000. La corteza continental está hecha para ti.
| Tipo de Roca | Volúmenes de minerales individuales en 1000 cm 3. | Gramos de minerales individuales en 1000 cm 3 | Peso Total (gramos) | Densidad (gramos por centímetro cúbico, g/cm 3) |
|---|---|---|---|---|
| Corteza Continental (Granito) | Cuarzo — 180 cm 3 Feldespato — 760 cm 3 Anfíbol — 70 cm 3 | Cuarzo — 477 g Feldespato — 1999 g Anfíbol — 277 g | 2703 g | 2.70 |
| Corteza Oceánica (Basalto) | Feldespato — 450 cm 3 Anfíbol — 50 cm 3 Piroxeno — 500 cm 3 | Feldespato — Anfíbol — Piroxeno — | ||
| Manto (Peridotita) | Piroxeno — 450 cm 3 Olivino — 550 cm 3 | Piroxeno — Olivino — |
Si la corteza continental (representada por granito) y la corteza oceánica (representada por basalto) son como balsas que flotan en el manto, ¿qué te dice esto sobre qué tan alto o bajo deben flotar?
Este concepto se ilustra en la Figura\(\PageIndex{6}\). La línea discontinua es para referencia, mostrando puntos a igual distancia del centro de la Tierra.

Consulte el Apéndice 3 para el Ejercicio 9.4 respuestas.
Atribuciones de medios
- Figuras 9.4.1, 9.4.2, 9.4.3abc, 9.4.6: © Steven Earle. CC POR.
- Figura\(\PageIndex{4}\): “Goteo de masilla tonta” © Eric Skiff. CC BY-SA.
- Figura\(\PageIndex{5}\): “PGR Paulson2007 Tasa de Elevación Litosférica por PGR” por NASA. Dominio público.


