8.8: ¿Se pueden conectar los marcos euleriano y lagrangiano?

\[R=R(x,y,z,t)\]

Para encontrar el cambio en la tasa de precipitación R en una parcela aérea a lo largo del espacio y el tiempo, podemos tomar su diferencial, que es un cambio infinitesimalmente pequeño en R:

\[d R=\frac{\partial R}{\partial t} d t+\frac{\partial R}{\partial x} d x+\frac{\partial R}{\partial y} d y+\frac{\partial R}{\partial z} d z\]

donde dt es un cambio infinitesimalmente pequeño en el tiempo y dx, dy y dz son infinitesimalmente pequeños cambios en x, y y z coordenadas, respectivamente, de la parcela.

Si dividimos la Ecuación [8.15] por dt, esta ecuación se convierte en:

\[\frac{d R}{d t}=\frac{\partial R}{\partial t}+\frac{\partial R}{\partial x} \frac{d x}{d t}+\frac{\partial R}{\partial y} \frac{d y}{d t}+\frac{\partial R}{\partial z} \frac{d z}{d t}\]

donde dx/dt, dy/dt y dz/dt describen la velocidad de la parcela aérea en las direcciones x, y y z, respectivamente.

Consideremos dos posibilidades:

Caso 1: La paquetería aérea no se mueve. Entonces el cambio en x, y y z son todos cero y:

\[\frac{d R}{d t}=\frac{\partial R}{\partial t}\]

Entonces, el cambio en la tasa de lluvias depende sólo del tiempo. \(\frac{\partial R}{\partial t}\)se llama derivado euleriano o hora local. Es el derivado del tiempo que cada una de nuestras estaciones de observación meteorológica registra.

Caso 2: La paquetería aérea se está moviendo. Entonces los cambios en su posición ocurren con el tiempo, y se mueve con una velocidad,\(\vec{U}=\vec{i} u+\vec{j} v+\vec{k} w,\) donde:

\[\frac{d x}{d t}=u \quad \frac{d y}{d t}=v \quad \frac{d z}{d t}=w\]

\[\frac{d R}{d t}=\frac{\partial R}{\partial t}+u \frac{\partial R}{\partial x}+v \frac{\partial R}{\partial y}+w \frac{\partial R}{\partial z}\]

Se le da un símbolo especial para el derivado cuando sigue el paquete aéreo alrededor. Se llama el derivado sustancial, o total, y se denota por:

\[\frac{D R}{D t}=\frac{\partial R}{\partial t}+u \frac{\partial R}{\partial x}+v \frac{\partial R}{\partial y}+w \frac{\partial R}{\partial z}\]

Matemáticamente, podemos expresar esta ecuación de una manera más general pensando en el producto punto de un vector con el gradiente de un escalar como lo hicimos en un ejemplo del operador del:

\[\frac{D R}{D t}=\frac{\partial R}{\partial t}+\vec{U} \cdot \vec{\nabla} R\]

donde al segundo término del lado derecho se le llama la derivada advectiva, que describe los cambios en las precipitaciones que se deben únicamente al movimiento de la parcela aérea a través de una distribución pluviométrica espacialmente variable.Debería poder demostrar que la ecuación [8.19] es la misma que la ecuación [8.18].

Podemos reorganizar esta ecuación para poner la derivada local a la izquierda.

\[\frac{\partial R}{\partial t}=\frac{D R}{D t}-\vec{U} \cdot \vec{\nabla} R\]

El término de la izquierda es la derivada de la hora local, que es el cambio en la variable R en una estación fija de observación. El primer término a la derecha es la derivada total, que es el cambio que se está produciendo en la parcela aérea a medida que se mueve. El último término a la derecha,\(-\vec{U} \cdot \vec{\nabla} R,\) se llama la advección de\(R\), Tenga en cuenta que la advección es simplemente lo negativo de la derivada advectiva.

Para volver a la analogía de la tormenta eléctrica, el cambio en las precipitaciones que observaste manejando en tu auto fue el derivado total del tiempo y solo dependía del cambio en la intensidad de la lluvia en la tormenta eléctrica. Sin embargo, para cada observador en una casa, el cambio en la tasa de lluvias dependía no sólo de la intensidad de la lluvia ya que la tormenta se encontraba sobre la casa sino también del movimiento de la tormenta eléctrica a través del paisaje.

R puede ser cualquier escalar. La tasa de precipitación es un ejemplo, pero las más utilizadas son la presión y la temperatura.

La ecuación [8.20] se llama relación de Euler y relaciona el marco euleriano con el marco lagrangiano. Los dos están relacionados por este nuevo concepto llamado advección.

Veamos la advección con más detalle, centrándonos en la temperatura.

Generalmente pensamos que la advección está en la horizontal. Muy a menudo solo consideramos los cambios en las direcciones x e y e ignoramos los cambios en la dirección z:

advección horizontal de la temperatura\[=-\vec{U}_{H} \cdot \vec{\nabla}_{H} T=-\left(u \frac{\partial T}{\partial x}+v \frac{\partial T}{\partial y}\right)\]

Entonces, ¿qué pasa con el signo menos? Veamos qué tiene sentido físico. Supongamos que T aumenta solo en la dirección x de manera que:

\[\frac{\partial T}{\partial y}=0\) and \(\frac{\partial T}{\partial x}>0\]

Si u > 0 (occidentales, soplando hacia el este), entonces tanto u como\(\frac{\partial T}{\partial x}\) son positivos para que la advección de temperatura sea negativa. ¿Qué significa esto? Significa que el aire más frío que sopla desde el oeste está reemplazando al aire más cálido, y la temperatura en nuestra ubicación está disminuyendo a partir de este aire avanzado. Así\(\frac{\partial T}{\partial t}\) debería ser

negativo ya que el tiempo va en aumento y la temperatura disminuye debido a la advección.

Si la advección de temperatura es negativa, entonces se llama advección de aire frío, o simplemente advección fría. Si la advección de temperatura es positiva, entonces se llama advección de aire caliente, o simplemente advección caliente.

Algunos ejemplos de casos simples de advección muestran estos conceptos (ver figura a continuación). Cuando el viento sopla a lo largo de las isotermas, la advección de temperatura es cero (Caso A). Cuando el viento sopla desde la dirección de una temperatura más baja a una temperatura más alta (Caso B), tenemos advección de aire frío. Cuando el viento sopla como alguna dirección no normal a las isotermas, entonces necesitamos multiplicar la magnitud del viento y el gradiente de temperatura por el coseno del ángulo entre ellas. Podemos estimar la advección de temperatura haciendo lo que hicimos para el gradiente, es decir, reemplazar todas las derivadas y derivadas parciales por Δs finitas.

Ejemplos de advección de temperatura horizontal para casos con diferentes ángulos entre la normal a las isotermas y la dirección del viento (en términos matemáticos). Cuando el gradiente de temperatura y la dirección del viento son paralelos, entonces la advección es máxima; cuando son perpendiculares, entonces es cero. El aire caliente que se mueve hacia el aire frío será una advección caliente; el aire frío que se mueve hacia el aire caliente será advección fría. Nota: v _H utilizado en esta figura es el mismo que U _H en el texto.

Crédito: H.N. Shirer

Cuando las isotermas con la misma diferencia de temperatura están más separadas en el mapa (ver figura abajo), entonces la advección de temperatura horizontal será menor que cuando las isotermas están más juntas, si la velocidad del viento es la misma en los dos casos.

Ejemplos de advección de temperatura horizontal para diferentes distancias entre las isotermas para una velocidad constante del viento. Nota: v _H utilizado en esta figura es el mismo que U _H en el texto.

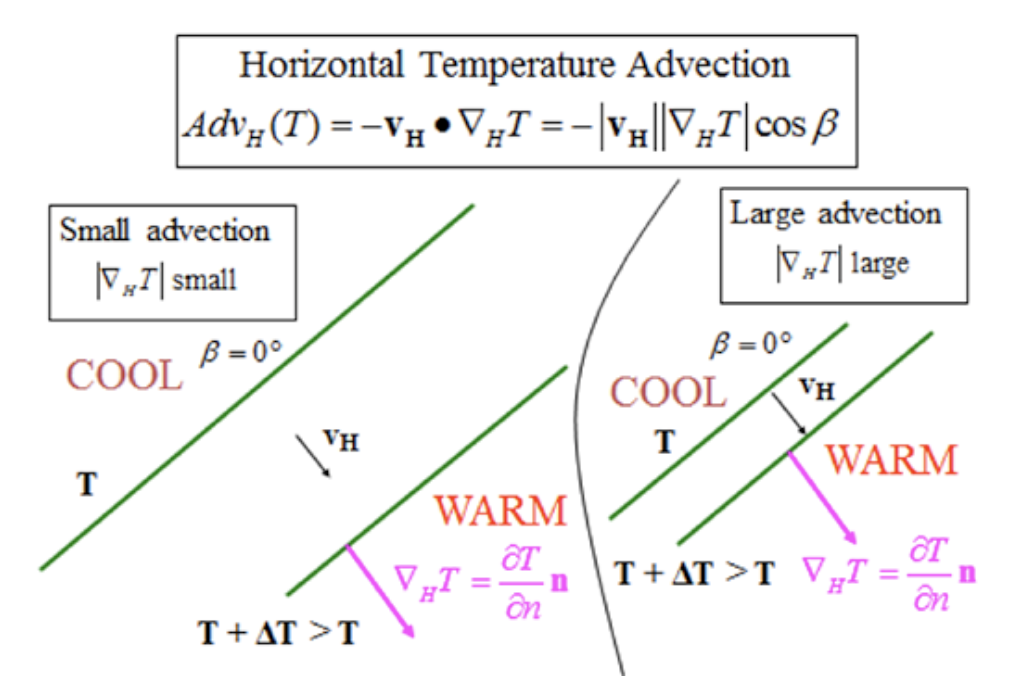
Crédito: H.N. Shirer

En resumen, para calcular la advección de temperatura, primero determinar la magnitud y la dirección del gradiente de temperatura. Segundo, determinar la magnitud y dirección del viento. La advección es simplemente el negativo del producto puntual de la velocidad y el gradiente de temperatura.

Vea este video (2:20) sobre el cálculo de la advección:

Encontrar Advección

Haga clic aquí para ver la transcripción del video Finding Advection.

La advección de temperatura es solo un producto puntual del vector de velocidad y el vector de gradiente de temperatura en ese punto. Escojamos este punto en Pensilvania donde ya calculamos el gradiente de este punto. Veamos el vector del viento. Entonces la trama meteorológica de la estación tiene una púa de viento que está al noroeste y cinco nudos. Y así podemos estimar, ya que ésta es dirección x, y como ésta es norte, podemos estimar que esto es de unos 300 grados en cuanto al ángulo de meteorología. Entonces, para encontrar el ángulo matemático, que es lo que necesitamos para el cálculo aquí, necesitamos tomar 270 grados. Y restamos 300 grados de eso, y obtenemos alfa es igual a menos 30, que es 330 grados si partimos del eje x y vamos en sentido antihorario todo el camino alrededor de esta dirección así. Ya nos dimos cuenta de que el gradiente tiene un ángulo que es de 301 grados, y eso es desde el eje x que va todo el camino alrededor. Entonces eso es algo así. Y por lo tanto, la diferencia entre ambos es de 29 grados. Y eso es beta. Sabemos que la magnitud del gradiente de temperatura es de 0.12 grados Fahrenheit. Entonces multiplicamos la magnitud de la velocidad por la magnitud del gradiente de temperatura por coseno de 29 grados. Terminamos obteniendo un valor de 0.52 y el signo menos grados Fahrenheit por hora. Entonces el signo menos está aquí, porque esto es positivo, positivo y positivo. Y así la advección es de menos 0.52 grados Fahrenheit por hora. Esto es advección de aire frío, o advección fría.

Quiz 8-4: La conexión de advección.

1. Encuentra Cuestionario de práctica 8-4 en Lienzo. Puedes completar este cuestionario de práctica tantas veces como quieras. No está calificado, pero le permite verificar su nivel de preparación antes de realizar el cuestionario calificado.
2. Cuando sientas que estás listo, toma Quiz 8-4. Se te permitirá realizar este cuestionario solo una vez. ¡Buena suerte!