10.8: ¿Por qué los mapas meteorológicos utilizan superficies de presión en lugar de superficies de altura?

No se puede encontrar un mapa meteorológico de vientos a 5000 m, pero se puede encontrar uno para 500 mb, que es aproximadamente la misma altitud que 5000 m (ver figura abajo).

Vientos de 500 mb para el 22 de febrero de 2015. Los números son de altura sobre el nivel del mar en decámetros (presa, decenas de metros). Por ejemplo, la altura de la superficie de 500 mb en el alto es de 5940 m = 594 presa.

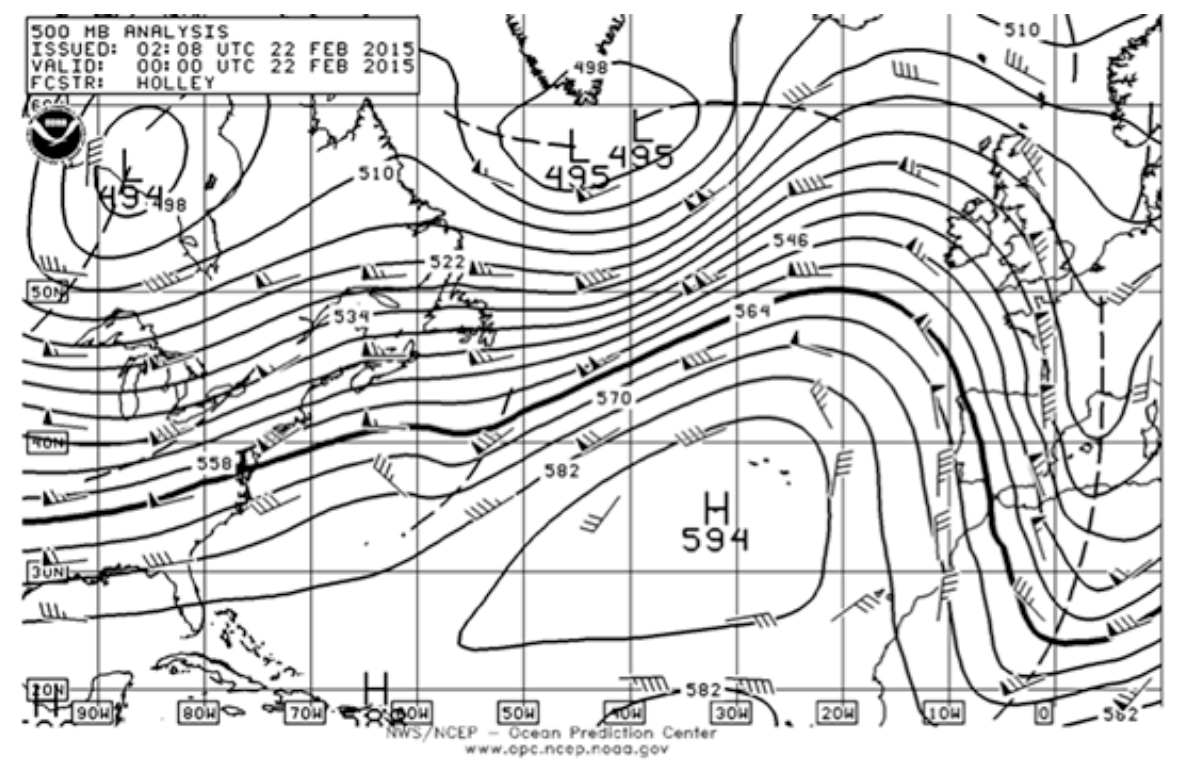
Crédito: NOAA

Aprenderemos por qué los mapas meteorológicos utilizan la presión como coordenada vertical, pero por ahora, mostraremos que altitudes más altas en una superficie de presión constante corresponden a presiones más altas en una superficie de altitud constante.

Si miramos hacia abajo en la Tierra, entonces podemos trazar las isobarras en función de la latitud (y) y la longitud (x). Podemos hacer una segunda gráfica de superficies de altura sobre una superficie de presión constante (ver figura a continuación). Generalmente la presión en promedio es mayor en el ecuador sobre una superficie de altura dada que en los polos. Esta inclinación tiene sentido si piensas en la ecuación de equilibrio hidrostático porque la temperatura es mayor en el ecuador que en los polos. Por lo tanto, la altura de la escala es mayor, por lo que la presión disminuye con la altura más gradualmente en el ecuador que en los polos.

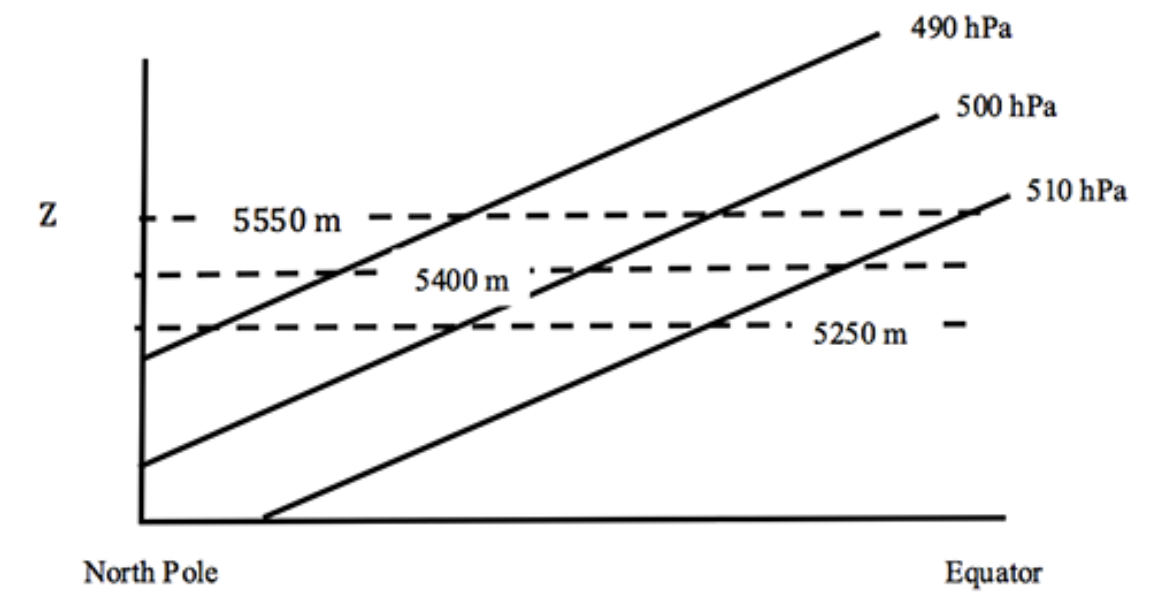
Un esquema de superficies de presión constante que se cruzan con superficies de altura constante desde el polo hasta el ecuador.

Crédito: W. Brune

Podemos elegir arbitrariamente una superficie de altura y ver cómo cambia la presión en función de la latitud. Vemos que aumenta de polo a ecuador (ver figura abajo).

Un esquema de isobarras (presión constante) en un mapa horizontal x — y a una superficie de altura constante de 5400 m, como en la figura anterior.

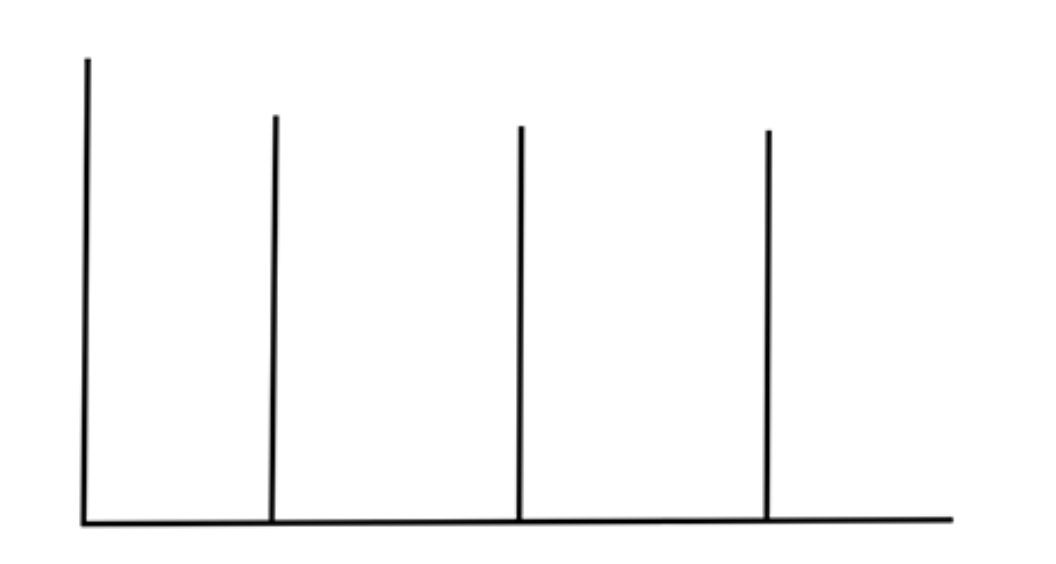
Crédito: W. Brune

Si ahora elegimos arbitrariamente una superficie de presión constante de, digamos, 500 mb, entonces el cambio en la altura en una gráfica horizontal x—y en la superficie de presión también muestra un aumento de polo a ecuador (ver figura a continuación).

Un esquema de isobarras (presión constante) en un mapa horizontal x — y a una superficie de altura constante de 5400 m, como en la figura anterior.

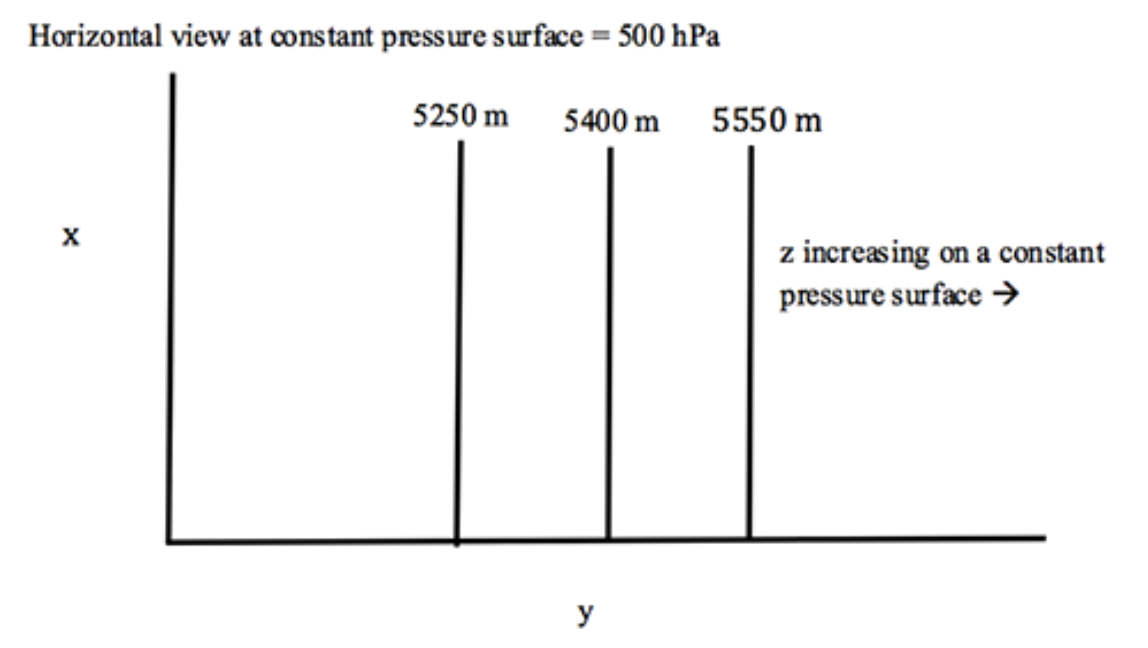
Crédito: W. Brune

Por lo tanto, la baja presión en las superficies de altura constante está relacionada con las bajas alturas en las superficies de presión constante. Como resultado de la aproximación hidrostática, por cada altura hay una presión única, por lo que podemos reemplazar z por p como coordenada vertical. Luego podemos observar los cambios en las variables en función de x e y, pero en lugar de hacerlo en una superficie de altura constante, podemos hacerlo sobre una superficie de presión constante.

Ahora podemos mostrar cómo cambian las ecuaciones de movimiento cuando la coordenada vertical se cambia de la altura, z, a la presión, p.

Considere primero la fuerza de gradiente de presión (PGF). La siguiente figura proporciona un esquema de la matemática.

Una sección transversal del cambio de presión en una superficie x—z. Tenga en cuenta que Δ x, Δ z y Δ p son todos positivos y Δ p es el mismo en horizontal y vertical.

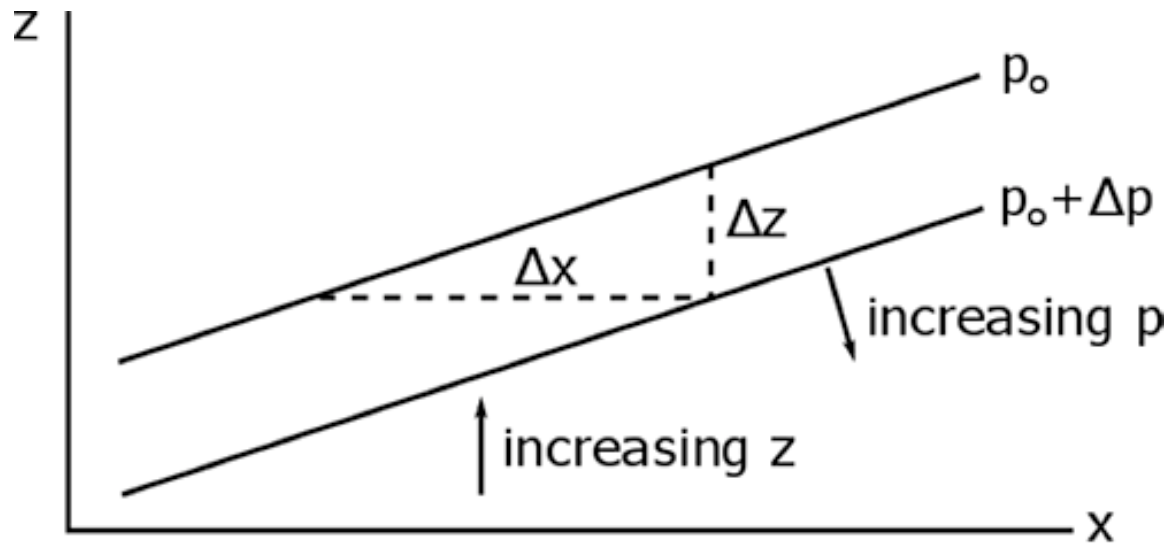
Crédito: W. Brune (después de R. Najjar)

La pendiente de la isobarra es solo el cambio en z dividido por el cambio en x en una isobar:

\[\frac{\Delta z}{\Delta x} \rightarrow\left(\frac{\partial z}{\partial x}\right)_{p}\]

donde el subíndice “p” significa “presión constante”. Dado que Δ p es el mismo en la vertical y en la horizontal:

\[\left(\frac{\partial p}{\partial x}\right)_{z} \Delta x=-\left(\frac{\partial p}{\partial z}\right)_{x} \Delta z\]

\[\left(\frac{\partial p}{\partial x}\right)_{z}=-\left(\frac{\partial p}{\partial z}\right)_{x}\left(\frac{\partial z}{\partial x}\right)_{p}\]

donde los subíndices "x" y "z" significan distancia constante hacia el este y altura constante, respectivamente.

Multiplicando ambos lados por 1/ρ y usando la ecuación de equilibrio hidrostático:

\[-\frac{1}{\rho}\left(\frac{\partial p}{\partial x}\right)_{z}=\frac{1}{\rho}\left(\frac{\partial p}{\partial z}\right)_{x}\left(\frac{\partial z}{\partial x}\right)_{p}=-g\left(\frac{\partial z}{\partial x}\right)_{p}\]

o

\[-\frac{1}{\rho}\left(\frac{\partial p}{\partial x}\right)_{z}=-g\left(\frac{\partial z}{\partial x}\right)_{p}\]

Lo mismo para la dirección y:

\[-\frac{1}{\rho}\left(\frac{\partial p}{\partial y}\right)_{z}=-g\left(\frac{\partial z}{\partial y}\right)_{p}\]

Entonces, el equilibrio geostrófico (Ecuación [10.24], [10.25]) en las coordenadas de presión se convierte en:

Ecuación x-momentum:\(0=-g \frac{\partial z}{\partial x}+f v\)

\(y\)-ecuación de impulso:\(0=-g \frac{\partial z}{\partial y}-f u\)

Estas ecuaciones se pueden reorganizar para dar la velocidad horizontal en la superficie de presión y se pueden reescribir como una en forma vectorial:

\(\overrightarrow{V_{g}}=\frac{g}{f} \vec{k} \times \vec{\nabla}_{p} z\)

donde\(\overrightarrow{V_{g}}\) se designa velocidad geostrófica y\(\vec{\nabla}_{p} z=\vec{i} \frac{\partial z}{\partial x}+\vec{j} \frac{\partial z}{\partial y}\) se encuentra en una superficie de presión constante.

Geopotencial

Podemos escribir estas ecuaciones de manera un poco diferente usando el concepto de geopotencial. Geopotencial, Φ, es la energía potencial por unidad de masa de una parcela aérea a una altura z, donde se define cero energía potencial en la superficie (z = 0).

\[\Phi=\int_{o}^{z} g d z\]

\[d \Phi=g d z\]

En forma vectorial, las velocidades se convierten en:

\[\vec{V}_{g}=\frac{1}{f} \vec{k} \times \vec{\nabla}_{p} \Phi\]

Equilibrio entre Coriolis y las fuerzas de gradiente de presión y las velocidades resultantes del viento en el Hemisferio Norte (NH) y Hemisferio Sur (SH).

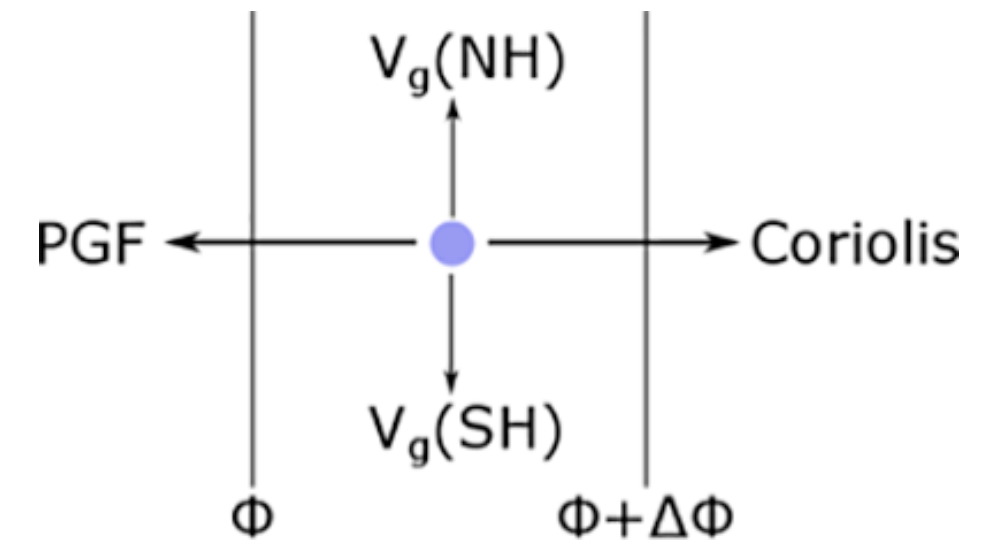
Crédito: W. Brune

Una ventaja importante de usar coordenadas de presión es que el gradiente de z o Φ es proporcional a todos\(\vec{V}_{g}\) los niveles de presión. Esta afirmación no es cierta para los gradientes de presión en los niveles de altura porque se debe conocer la densidad, ρ, como en las Ecuaciones [10.24] y [10.25], que varía drásticamente con la altura.

El siguiente video (1:19) proporciona una buena visión general de las superficies de presión:

Superficies de Presión

Haga clic aquí para ver la transcripción del video Superficies de Presión.

Este esquema muestra la relación entre las superficies de altura y las superficies de presión. Por lo general, las superficies de presión se inclinan hacia abajo en altura desde el ecuador, donde es más cálido, hasta el poste, donde hace más frío. Pudiste mostrar esto en la Actividad 2.2, y lo viste de nuevo en la Lección 2.4 sobre grosor. Tenga en cuenta que en la superficie de altura constante, desde el ecuador hasta el polo, la superficie de presión disminuye con la latitud. Ahora también, sobre una superficie de presión constante desde el ecuador hasta el polo, la superficie de altura disminuye sobre la superficie de presión constante. Así, los cambios en la presión son proporcionales a los cambios en la altura. Después de un poco de matemáticas, podemos demostrar que 1/rho —es decir, uno sobre la densidad— veces el cambio de presión con respecto a x o y en una superficie de altura es igual a g veces el cambio en z con respecto a x o y en una superficie de presión constante. Por último, observamos que gdz es solo un diferencial del geopotencial phi, que tiene unidades de metros cuadrados por segundo cuadrado, que son las mismas unidades que la energía dividida por masa. Por lo tanto, los cambios de altura en una superficie de presión constante son los mismos que los cambios en el geopotencial en una superficie de presión constante.