5.5.1: Flujo másico o impulso inducidos por olas
- Page ID
- 91419
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Las olas que se propagan no solo transportan energía a través de la superficie del océano, sino también impulso. El momento se define como el producto de la masa y la velocidad. Puede pensarse como masa en movimiento o un transporte de masa o flujo: una partícula de agua tiene una masa, y si la partícula se está moviendo tiene impulso. El momento por unidad de volumen se puede escribir así como el producto de la densidad de masa\(\rho\) y la velocidad\(\vec{u} = (u_x, u_y, w)\) de las partículas de agua. Momentum (por unidad de volumen)\(\rho \vec{u} = (\rho u_x, \rho u_y, \rho w)\) es una cantidad vectorial, una cantidad que se describe completamente tanto por magnitud como por dirección. La dirección del vector de impulso es la misma que la dirección del vector de velocidad.
La cantidad total de impulso de onda por unidad de área de superficie en la dirección de propagación de la ola se obtiene por integración a lo largo de la profundidad. Promediado a lo largo del tiempo esto da (con\(u\) la velocidad orbital horizontal en la dirección de propagación de la onda):
\[q = \overline{\int_{-h}^{\eta} \rho u dz}\label{eq5.5.1.1}\]
Solo hay una contribución al impulso desde el nivel de canal de ola hasta el nivel de cresta de ola, ya que por debajo del canal de ola la velocidad varía armónicamente en el tiempo (ver Secc. 5.4.1), dando un resultado promediado en el tiempo cero. Si medimos la velocidad en algún punto por encima de MSL solo registraremos velocidades durante parte del período de onda y todas las grabaciones serán positivas (y en la dirección de propagación de la onda). Entre el nivel de canal de onda y MSL registraremos velocidades para una mayor parte del período de onda y aunque una parte de la grabación será negativa, la velocidad media promedio de onda seguirá siendo positiva. Por lo tanto, el momento\(q\) puede interpretarse como un flujo neto de masa entre el canal de ola y la cresta de ola asociado con la propagación de la ola.
Podemos calcular la integral de la Eq. \(\ref{eq5.5.1.1}\)para un solo componente armónico (no ruptura) sustituyendo la velocidad de acuerdo con la teoría de ondas lineales (ver Ec. 5.4.1.1) en\(z = 0\) e integrando de\(z = 0\) a la elevación instantánea de la superficie\(\eta = a \cos \omega t\). Luego encontramos para el momento medio en un plano perpendicular a la dirección de propagación de la onda por unidad de área de superficie:
\[q_{\text{non-breaking}} = \overline{\int_0^{a \cos \omega t} \rho \dfrac{a \omega}{\tanh kh} \cos \omega t dz} = \overline{a \cos \omega t \rho \dfrac{a \omega}{\tanh kh} \cos \omega t} = \dfrac{\rho a^2 \omega}{2\tanh kh} = \dfrac{\rho g a^2}{2c} = \dfrac{E}{c}\label{eq5.5.1.2}\]
Esta expresión muestra que\(q\) es una cantidad no lineal en la amplitud\(a\). El resultado es válido con precisión de segundo orden en la amplitud (la teoría de ondas lineales es de primer orden). Aparentemente, el flujo másico inducido por ondas ocurre incluso para un movimiento orbital sinusoidal perfecto, pero es un efecto de segundo orden. En la aproximación lineal, de pequeña amplitud,\(q\) es cero y la propagación de ondas es meramente una cuestión de movimiento de la forma de onda, no de masa. En relación con el flujo másico neto asociado a la propagación de ondas, a menudo se usa el término deriva de Stokes (ver Intermezzo 5.3).
La ecuación\(\ref{eq5.5.1.2}\) es válida fuera de la zona de surf. En la zona de olas el flujo másico es sustancialmente mayor que fuera de la zona de oleaje. Se supone que consta de dos partes, una por el carácter progresivo de las ondas (Ec. \(\ref{eq5.5.1.2}\)) y el otro debido al rodillo de superficie en ondas rompientes:
\[q_{\text{drift}} = q_{\text{non-breaking}} + q_{\text{roller}} = \dfrac{E}{c} + \dfrac{\alpha E_r}{c}\label{eq5.5.1.3}\]
En esta ecuación,\(E_r\) está la energía del rodillo. La primera parte del lado derecho es el flujo másico para ondas no rompientes, mientras que la segunda parte representa la contribución de la masa del rodillo de superficie. Diversos autores han argumentado valores para el factor\(\alpha\) en la Ec. \(\ref{eq5.5.1.3}\)para estar en el rango de 0.22 a 2 (Nairn et al., 1990; Roelvink & Stive, 1989). Sus argumentos están demasiado involucrados para tratarlos en este curso y aquí asumimos que\(\alpha\) es el orden 1.
En el caso de un límite cerrado como una costa, hay un transporte masivo neto cero a través de la vertical ya que de lo contrario el agua se amontonará cada vez más contra la costa. Esto significa que debe haber una velocidad neta por debajo del nivel de canal de la ola para compensar el flujo por encima del nivel de canal de la ola: una corriente de retorno. La velocidad media de profundidad transversal por debajo del nivel de canal de la ola debe compensar el flujo másico perpendicular a la costa y, por lo tanto, viene dada por:
\[U_{\text{below through}} = -\dfrac{q_{\text{drift}, x}}{\rho h} = -\dfrac{q_{\text{drift}} \cos \theta}{\rho h}\]
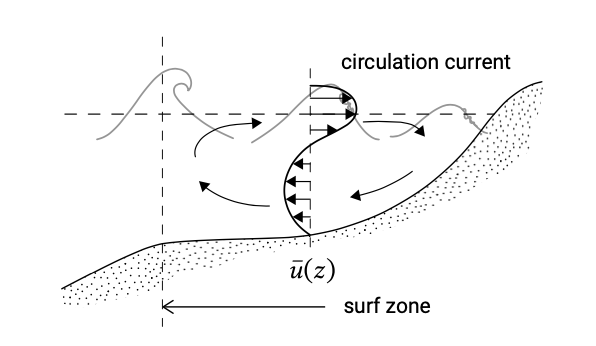
Al romper las olas, el transporte masivo hacia la costa entre la cresta de ola y el canal de ola puede ser bastante grande, resultando en velocidades dirigidas hacia el mar bastante grandes bajo el nivel de la ola (ver Fig. 5.25). La gran corriente de retorno en la zona de surf se llama resaca.

También en el caso bidimensional de un canal de olas de laboratorio, la misma masa de agua tiene que regresar nuevamente al 'mar'. En la parte inferior de la columna de agua esto da un flujo de retorno (ver Fig. 5.26). La figura también muestra el streaming de Longuet-Higgins cerca de la cama (ver Secc. 5.4.3). En la Fig. 5.25, hemos asumido que en la zona de oleaje el streaming constante de Longuet-Higgins bien puede ser anulado por la resaca. La distribución sobre la profundidad de la corriente de retorno o resaca (y la transmisión) se puede resolver usando una ecuación de impulso horizontal (¡no promediada en profundidad!) , véase la Secc. 5.5.6.
El Apéndice B proporciona un ejemplo de experimentos de canal de olas de ondas periódicas y aleatorias en una playa de suave pendiente (Stive, 1985). La Figura B.2 muestra las mediciones de las corrientes de retorno en bajío y rompiendo ondas periódicas. En las olas no rompientes hay una corriente de retorno relativamente pequeña. Al romper las olas, el transporte masivo hacia la costa entre la cresta de ola y el canal de ola puede ser bastante grande, lo que resulta en velocidades medias de tiempo dirigidas hacia el mar bastante grandes bajo el nivel de la ola.
Explicamos el transporte masivo desde un punto de vista euleriano en el texto anterior (colocando un poste de medición en una sección transversal fija y concluyendo que por encima del nivel de canal de la ola la velocidad registrada tiene un resultado promedio en el tiempo distinto de cero en la dirección de propagación de la onda). También se puede explicar desde un punto de vista lagrangiano, a saber, siguiendo una partícula de agua que se mueve en su movimiento orbital (ver Fig. 5.20). Dado que el movimiento horizontal es en general más pequeño más cerca de la cama (ver Eq. 5.22 y Fig. 5.21), la partícula de agua se mueve más rápido en la dirección de propagación de la ola cuando se encuentra debajo de la cresta de la ola, que corre hacia atrás cuando está debajo del canal de la ola. Como resultado, las trayectorias de partículas no son órbitas completamente cerradas y hay un movimiento residual en la dirección de propagación de la onda durante un período de onda. Este movimiento residual se conoce como deriva de Stokes y da lugar a un transporte de masa neta en la dirección de propagación de las olas. Cuando integramos el transporte masivo lagrangiano sobre la vertical obtenemos el mismo resultado que el transporte masivo euleriano por encima del nivel del canal de olas.
La resaca es importante para el transporte de sedimentos hacia el mar debido a la relativamente alta velocidad dirigida fuera de la costa en la parte baja y media de la columna de agua en una zona con concentraciones de sedimentos relativamente altas (debido a la ruptura de las olas). Se cree que la resaca es responsable de la severa erosión de las playas durante las fuertes tormentas. El transporte de sedimentos debido a las corrientes de retorno también es importante para las áreas poco profundas que tienen un área más profunda entre ellas y la costa. Ejemplos son las áreas poco profundas en los deltas ebb-mareales de los sistemas de entrada costeros, donde el flujo másico no está (completamente) compensado por la resaca ya que el agua puede fluir en la parte posterior de estos pisos (donde a menudo hay canales de marea). Esto se discute más a fondo en la Secc. 9.4.1.


