5.5.2: Estrés por Radiación
- Page ID
- 91438
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La segunda ley de Newton establece que la tasa de cambio de impulso de un elemento fluido es igual a las fuerzas sobre el elemento. Las ondas pueden cambiar el momento a través de la 'entrada' neta o la 'salida' del momento, ya sea por la entrada neta o la salida del momento con la velocidad de la partícula o a través de una fuerza de presión neta inducida por la onda. Estrés por radiación es el nombre que se le ha dado al flujo (o flujo) de impulso integrado en profundidad y promedio de onda debido a las olas. Primero fue definido por Longuet-Higgins y Stewart (1964) como el exceso de flujo de impulso debido a la presencia de olas.
Si hay cambio en el flujo de impulso inducido por las olas (tensión de radiación) de una ubicación a otra, las fuerzas de las olas actúan sobre el fluido, impactando el movimiento medio del agua y los niveles. Estas fuerzas de ola son responsables de:
- bajar el nivel medio del agua en la zona de bajío (demarcación);
- elevar el nivel medio del agua en la zona de surf (puesta a punto);
- conducir una corriente longshore en el caso de olas que se aproximan oblicuamente a la orilla (1 m/s bajo algunas condiciones).
Definición de componentes de estrés por radiación
El flujo horizontal de impulso inducido por olas a través de un plano vertical en una ubicación dada consiste en:
- la transferencia de impulso\(\rho \vec{u}\) a través de ese plano con la velocidad de partícula normal a ese plano;
- la fuerza de presión inducida por olas que actúa sobre el plano debido a la presión inducida por la ola\(p_{\text{wave}}\) en el agua.
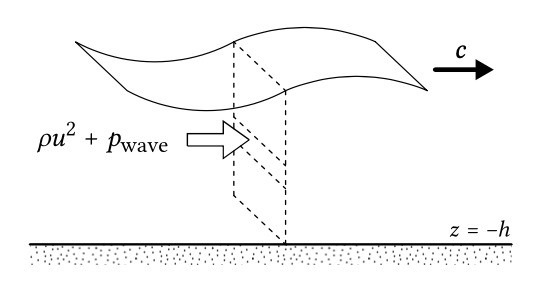
Primero supongamos que el plano en consideración es perpendicular a la propagación de la onda (Fig. 5.27). La presión inducida por olas\(p_{\text{wave}}\) actúa por definición normal al plano. Además, a cada altura por encima del lecho, la velocidad de la partícula\(u\) transporta el momento\(\rho u\) a través del plano (por unidad de longitud de cresta).

Figura 5.28: Sistema de coordenadas y vector de velocidad.
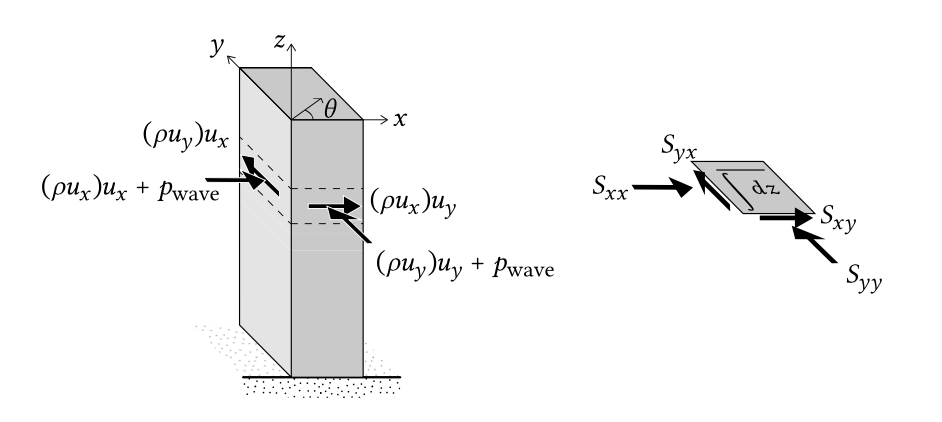
Figura 5.29: Esquema de los componentes de transporte de momento y tensión de radiación en cierto punto en\(x,y\) el espacio para ondas oblicuamente incidentes. Las tensiones de radiación se obtienen integrando el transporte de impulso sobre la columna de agua y promediando en el tiempo.
Ahora considere un sistema de coordenadas de acuerdo con la Fig. 5.28. La onda se propaga en ángulo con el\(x\) eje. La velocidad de la partícula tiene un componente\(u_x\) en la\(x\) dirección -y un componente\(u_y\) en la\(y\) dirección -dirección. La velocidad de la partícula\(u_x\) transporta tanto\(x\) -momentum\(\rho u_x\) como\(y\) -momentum\(\rho u_y\). El transporte de\(x\) -momentum por la velocidad de la partícula\(u_x\) a través de un plano vertical perpendicular al\(x\) eje (por unidad de tiempo y por unidad de área) es\((\rho u_x) u_x\) y el transporte de\(y\) -momentum a través del plano es\((\rho u_y) u_x\). Los flujos de impulso se pueden ver en la parte izquierda de la Fig. 5.29).
La Figura 5.29 visualiza los componentes de transporte de impulso y tensión\(x\) de radiación en dirección y\(y\) dirección en cierto punto en\(x,y\) el espacio. El transporte de impulso a través de todo el plano por unidad de longitud de cresta se obtiene por integración sobre la profundidad desde el fondo hasta la superficie instantánea del agua. Rendimientos promediados en el tiempo para el transporte promedio de onda total de\(x\) -momentum en la\(x\) dirección -o la tensión de radiación\(S_{xx}\):
\[S_{xx} = \underbrace{\overline{\int_{-h_0}^{\eta} (\rho u_x) u_x dz}}_{\text{part due to advection by horizontal particle velocity}} + \underbrace{\overline{\int_{-h_0}^{\eta} p_{\text{wave}} dz}}_{\text{pressure part}}\label{eq5.5.2.1}\]
\(S_{xx}\)actúa de manera normal al plano considerado y, por lo tanto, es un componente normal de la tensión de radiación. Es equivalente a una tensión normal que actúa en la\(x\) dirección -dirección.
El componente de tensión de radiación\(S_{xy}\) (el componente de cizallamiento de la tensión de radiación) se define como el transporte de\(x\) impulso en la\(y\) dirección. Actúa como esfuerzo cortante en el plano (se dirige en la\(x\) dirección -y trabaja en el plano normal a la\(y\) dirección -) y viene dada por:
\[S_{xy} = \overline{\int_{-h_0}^{\eta} (\rho u_x) u_y + \tau_{xy} dz}\]
El esfuerzo cortante debido a las olas es cero para un fluido ideal irrotacional de manera que tenemos:
\[S_{xy} = \overline{\int_{-h_0}^{\eta} (\rho u_x) u_y dz} \label{eq5.5.2.3}\]
Consiste en una contribución debida a la advección por la velocidad orbital horizontal solamente. Tenga en cuenta que para el caso especial de ondas normalmente incidentes, la\(x\) dirección -dirección es la dirección de propagación de la onda,\(u_y\) y por lo tanto\(S_{xy}\) son cero.
Considerando un plano normal a la\(y\) dirección, encontramos para los flujos de impulso en la\(y\) dirección, el componente normal:
\[S_{yy} = \underbrace{\overline{\int_{-h_0}^{\eta} (\rho u_y) u_y dz}}_{\text{part due to advection by horizontal particle velocity}} + \underbrace{\overline{\int_{-h_0}^{\eta} p_{\text{wave}} dz}}_{\text{pressure part}}\]
y el componente de cizallamiento:
\[S_{yx} = \overline{\int_{-h_0}^{\eta} (\rho u_y) u_x dz} \label{eq5.5.2.5}\]
En el caso especial de que la\(x\) -dirección es la dirección de propagación de la onda se\(u_y = 0, S_{yy}\) reduce a la parte de presión y\(S_{yx} = S_{xy} = 0\).
Expresiones de estrés por radiación usando teoría de ondas lineales
Mediante el uso de la teoría de ondas lineales (primer orden), se pueden obtener expresiones para la tensión de radiación que son válidas para segundo orden. La derivación completa se puede encontrar en Holthuijsen (2007). Intermezzo 5.4 da un extracto de esta derivación.
Es más fácil partir de una onda que se propaga en\(x\) dirección positiva para que\(u_x = u\) y\(u_y = 0\). Si sustituimos por\(u = \hat{u} \cos (\omega t - kx)\)\(\hat{u}\) según la Secc. 5.4.1 en la parte de velocidad de partícula de la Ec. \(\ref{5.5.2.1}\)encontramos (ver Holthuijsen (2007) para la derivación):
\[S_{xx, \text{horizontal particle velocity}} = \overline{\int_{-h_0}^{\eta} (\rho u^2) dz} \approx \int_{-h_0}^{0} \rho \overline{u^2} dz = nE\]
donde:
| \(S_{xx}, \text{hor, part, vel.}\) | tensión de radiación en la dirección de propagación de la onda debido a la advección del momento por el movimiento orbital horizontal | \(N/m\) |
| \(n\) | relación de velocidad de grupo y velocidad de fase | - |
| \(E\) | energía de las olas en la columna de agua por\(m^2\) | \(J/m^2\) |
En el caso de ondas irregulares esta ecuación se puede aplicar utilizando\(E = 1/8 \rho g H_{rms}^2\). Para el flujo másico encontramos una contribución cero para cada nivel por debajo del canal de la ola porque\(\bar{u} = 0\). Sin embargo, el flujo de impulso es distinto de cero para toda la profundidad del agua desde entonces\(\overline{u^2} \ne 0\). Varía en principio sobre la profundidad. Solo en aguas poco profundas, donde la velocidad orbital horizontal se distribuye uniformemente, la parte de la velocidad de la partícula de la tensión de radiación se distribuye uniformemente.
La presión para cualquier nivel por debajo del canal daría un resultado promedio de tiempo cero de acuerdo con la teoría lineal. Sin embargo, existe una contribución a la presión inducida por la onda promediada en el tiempo\(\overline{p_{\text{wave}}}\) debido al flujo vertical de impulso por el movimiento vertical del fluido. Esto puede pensarse como el movimiento oscilatorio vertical del fluido que ayuda a llevar el peso de la columna de agua y viene dado por\(-\rho \overline{w^2}\), en el que\(w\) se encuentra la velocidad orbital vertical. La contribución al estrés de radiación se puede encontrar sustituyendo la expresión lineal por\(w\) e integrándola al nivel medio del agua. Encontramos:
\[S_{xx, \text{pressure, 1}} = -\overline{\int_{-h_0}^{\bar{\eta}} \rho w^2 dz} \approx -\int_{-h_0}^{0} \rho \overline{w^2} dz = (n - 1)E\]
Además, hay una contribución a la tensión de radiación debido a las fluctuaciones de presión entre el canal de onda y el nivel de cresta de onda. En la Secc. 5.4.2 asumimos que la presión entre el canal de onda y el nivel de cresta fluctúa como\(\tilde{p} = \rho g \eta\). Esto da la siguiente contribución neta al estrés por radiación:
\[S_{xx, \text{pressure, 2}} = \overline{\int_{0}^{\bar{\eta}} \rho g \eta dz} = \dfrac{1}{2} \rho g \overline{\eta^2} = \dfrac{1}{2} E \label{eq5.5.2.8}\]
Esto da para la parte de presión de las tensiones de radiación:
\[S_{xx, \text{pressure}} = \underbrace{(n - 1)E}_{\text{contribution due to (depth-varying) vertical momentum flux}} + \underbrace{1/2 E}_{\text{contribution at top of water column}} = (n - 1/2) E\label{eq5.5.2.9}\]
El término\(\overline{w^2}\) varía en principio con la profundidad del agua, mientras que la otra parte (de la Ec. \(\ref{eq5.5.2.8}\)) se encuentra en la parte superior de la columna de agua. En aguas poco profundas (\(n = 1\)) las velocidades orbitales verticales son cero y la parte de presión de las tensiones de radiación se reduce a una contribución\(S_{xx, \text{pressure}} = 1/2 E\) en la parte superior de la columna de agua. En aguas profundas donde se encuentra\(n = 1/2\) el componente de presión a la tensión de radiación\((n - 1/2) E\).
La tensión total de radiación en la dirección de propagación de la onda (\(x\)-dirección) es ahora:
\[S_{xx} = S_{xx, \text{pressure}} + S_{xx, \text{horizontal particle velocity}} = (n -1/2) E + nE \label{eq5.5.2.10}\]
Las tensiones normales a la dirección de propagación de la onda\(S_{yy}\) consisten\((n - 1/2) E\) únicamente en la parte de presión. Los esfuerzos cortantes son cero.
De Intermezzo 5.4 — o más específicamente de la Ec. \(\ref{eq5.5.2.10}\)— concluimos que:
- La parte de presión de la tensión de radiación es igual a\((n - 1/2) E\). Dado que la presión es un escalar este término forma parte de las tensiones normales de radiación en todas las direcciones.
- La magnitud de la parte advectiva de la tensión de radiación, la parte debida al transporte de impulso por la velocidad de la partícula, es\(nE\). Es por definición en la dirección de propagación de la onda.
Con este resultado, ahora podemos deducir las expresiones más generales para los componentes de tensión de radiación para ondas que viajan en una dirección\(\theta\) relativa a la\(x\) dirección positiva (ver Fig. 5.28). Si el\(x\) eje -no es la dirección de propagación que tenemos\(\vec{u} = (u_x , u_y) = (u \cos \theta, u \sin \theta)\) y con Eqs. \(\ref{eq5.5.2.1}\),\(\ref{eq5.5.2.3}\) y\(\ref{eq5.5.2.5}\) encontramos:
\[S_{xx} = (n - \dfrac{1}{2} + n \cos^2 \theta) E \label{eq5.5.2.11}\]
\[S_{yy} = (n - \dfrac{1}{2} + n \sin^2 \theta) E\]
\[S_{xy} = S_{yx} = n \cos \theta \sin \theta E \label{eq5.5.2.13}\]
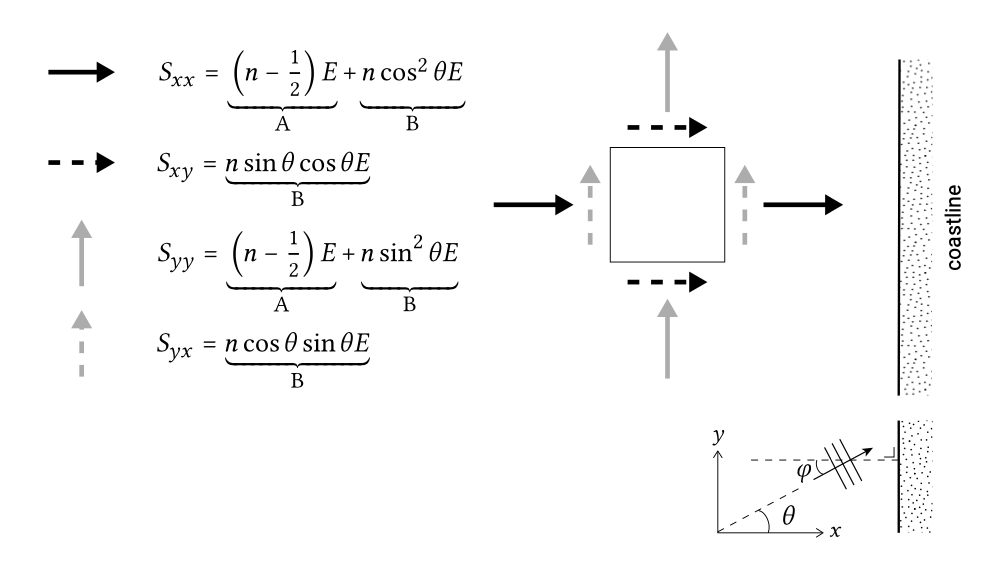
En la situación de costa uniforme a lo largo de la costa, la\(x\) dirección positiva generalmente se toma como la dirección normal de la costa y la\(y\) dirección positiva es paralela a la línea costera. El ángulo de incidencia de la onda\(\varphi\) con respecto a los contornos de profundidad es ahora igual al ángulo\(\theta\) con el\(x\) eje positivo. Para esa situación, los componentes de tensión de radiación se esbozan en la Fig. 5.30.
Tenga en cuenta que si el\(x\) eje coincide con la dirección de propagación de la onda (= 0), las ecuaciones anteriores. \(\ref{eq5.5.2.11}\)para\(\ref{eq5.5.2.13}\) reducir a:
\[S_{xx} = (2n - 1/2) E\]
\[S_{yy} = (n - 1/2) E \ \ \text{for waves propagating in the } x\text{-dircetion}\]
\[S_{xy} = S_{yx} = 0\]
Esto está de acuerdo con las conclusiones anteriores de que:
- Las tensiones normales perpendiculares a la dirección de propagación de la onda consisten\((n - 1/2) E\) únicamente en la parte de presión;
- Las tensiones normales en la dirección de propagación de la onda consisten en la parte de presión\((n - 1/2) E\) más la parte debida a la transferencia de impulso por el movimiento orbital horizontal\(n E\);
- Las tensiones cortantes son cero si la\(x\) dirección es la dirección de propagación de la onda.
En aguas profundas donde\(n = 1/2\), el componente de presión a la tensión de radiación es\((n - 1/2)E = 0\) y la parte de partículas de fluido se convierte\(n E = 1/2 E\) en la dirección de propagación de la onda. Así, en el caso de propagación de ondas en la\(x\) dirección -dirección, encontramos\(S_{xx} = 1/2 E\), y\(S_{yy} = 0\). En aguas poco profundas, por otro lado, donde\(n = 1\), se deduce que\(S_{xx} = 3/2 E\), y\(S_{yy} = 1/2 E\). Aquí ambas contribuciones se suman al estrés total de radiación\(S_{xx}\) y\(S_{yy}\) es igual a la parte de presión. El estrés por radiación (normal) en aguas poco profundas es claramente mayor que en aguas profundas. Y, tiene dos componentes en aguas poco profundas: paralela y perpendicular a la dirección de propagación de las olas.
Estrés por radiación en olas rompientes
Al romper las olas de la zona de surf, el efecto del rodillo de superficie será retrasar la liberación de impulso de la ruptura de la ola. En la práctica esto significa que las ecuaciones para las tensiones de radiación también contendrán un término debido a la energía del rodillo. Existen diferentes modelos para este término, potenciando ya sea la parte de presión o la parte de advección de la tensión de radiación o ambas. Svendsen (1984) propone una contribución adicional a la tensión de radiación en la dirección de propagación debido a la velocidad en el rodillo en una cantidad\(q_{\text{roller}} c = \alpha E_r\) (ver Eq. \(\ref{eq5.5.2.9}\)). Este aporte se concentra cerca de la superficie del agua donde se produce el rompimiento de la ola. Bajo el supuesto de aguas poco profundas, la tensión de radiación por debajo del nivel de canal de la ola está dominada por la parte debido a la advección del momento por el movimiento orbital horizontal (verificar esto desde Intermezzo 5.4). Dado que en aguas poco profundas la velocidad orbital horizontal se distribuye uniformemente, la parte advectiva de la tensión de radiación también se distribuye uniformemente.


