8.10: Derivabilidad y los conectivos proposicionales
- Page ID
- 103673
Comprobante.
-
Ambos secuentes\(A \land B \Sequent A\) y\(A \land B \Sequent B\) son derivables:

-
Aquí hay una derivación del secuente\(A, B \Sequent A \land B\):
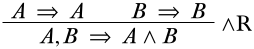
◻
-
\(A \lor B, \lnot A, \lnot B\)es inconsistente.
-
Ambos\(A \Proves A \lor B\) y\(B \Proves A \lor B\).
Comprobante.
-
Damos una derivación del secuente\(A \lor B, \lnot A, \lnot B \Sequent\):
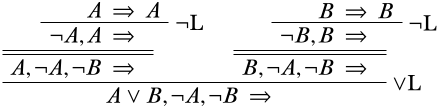
(Recordemos que las líneas de inferencia dobles indican varias inferencias de debilitamiento, contracción e intercambio).
-
Ambos secuentes\(A \Sequent A \lor B\) y\(B \Sequent A \lor B\) tienen derivaciones:

◻
Comprobante.
-
El secuente\(A \lif B, A \Sequent B\) es derivable:
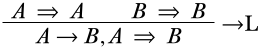
-
Ambos secuentes\(\lnot A \Sequent A \lif B\) y\(B \Sequent A \lif B\) son derivables:
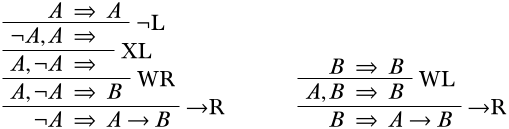
◻


