12.3: La lógica de solo en la lógica de clase

Última actualización
Guardar como PDF

Page ID: 102248

Bradley H. Dowden
California State University Sacramento

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Considera si estas dos frases son lógicamente equivalentes:

Sólo los estadounidenses son tejanos.
Sólo los tejanos son estadounidenses.

No son equivalentes. Una manera de decir es que en el mundo real uno es verdadero y otro es falso. Lógicamente las oraciones equivalentes son verdaderas juntas o falsas juntas. La primera frase dice: “Si estás en la clase de los tejanos, entonces estás en la clase de los estadounidenses”. La segunda frase dice: “Si estás en la clase de los estadounidenses, entonces estás en la clase de los tejanos”.

Los diagramas pueden ser útiles para demostrar las relaciones lógicas de oraciones que contienen solo la palabra complicada. Que TX sea el conjunto o clase de tejanos, y que Estados Unidos sea el conjunto de estadounidenses. Entonces “Solo los estadounidenses son tejanos” tiene este diagrama:

Un círculo etiquetado como “USA” dentro del cual se encuentra el contorno del estado de Texas con la etiqueta “TX”. TX está totalmente dentro de EE. UU.

y “Solo los tejanos son estadounidenses” tiene este diagrama:

Un círculo etiquetado como “USA” que está totalmente dentro del contorno del estado de Texas con la etiqueta “TX”.

Ahora bien es claro que las dos frases no están diciendo lo mismo y así no son lógicamente equivalentes. Si dijeran lo mismo, tendrían el mismo diagrama.

¿Estaría bien decir que solo los europeos son griegos? Hmm. Volveremos a esta pregunta en un momento.

Ejercicio\(\PageIndex{1}\)

Utilice la técnica de diagrama Venn-Euler para mostrar la validez o invalidez del siguiente argumento:

Sólo los seres vivos tienen hijos.
Una computadora no tiene hijos.
Entonces, una computadora no es un ser vivo.

Responder: El argumento no es válido porque en el siguiente diagrama las premisas salen verdaderas pero la conclusión no:

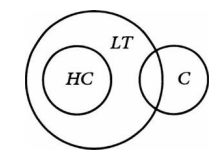
HC = la clase de cosas que tienen hijos
LT = los seres vivos
C = computadoras

Para abstraer de estos ejemplos, los puntos principales sobre la lógica de la palabra solamente son que la instrucción lógica de clase

Solo A son B

es lógicamente equivalente a la instrucción lógica de clase

Todas las B son A's.

Ambas declaraciones son equivalentes a la declaración condicional

Si algo es una B, entonces es una A.

Ejercicio\(\PageIndex{2}\)

Cree un contraejemplo para el siguiente argumento produciendo un argumento lógicamente análogo que es más obviamente inválido:

Sólo los simbidianos son griegos. Entonces, sólo los griegos son simbidianos.

Responder: Consideremos la situación en la que un “simbidiano” es un europeo. En esta situación, el argumento tiene una premisa verdadera y una conclusión falsa. Yo hice la palabra Simbidian; no la encontrarás en el diccionario.

Ahora examinemos algunos argumentos complicados que dependen crucialmente de la palabra solamente. ¿Es válido deductivamente el siguiente argumento?

Sólo los seres vivos pueden tener sentimientos.
Una computadora no es un ser vivo.
Entonces, una computadora no puede tener sentimientos.

Además, ¿es válido el siguiente argumento?

Sólo los seres vivos pueden tener sentimientos.
Una computadora no tiene sentimientos.
Entonces, una computadora no es un ser vivo.

Ambos argumentos parecen ser válidos para muchas personas que tienen ciertos puntos de vista sobre la inteligencia artificial. Sin embargo, estas personas están siendo ilógicas.

Ejercicio\(\PageIndex{3}\)

¿Alguno de los dos argumentos anteriores sobre computadoras tiene validez deductiva?

Responder: El primer argumento es válido.

Aunque el método del diagrama Venn-Euler es muy poderoso, tiene limitaciones en comparación con los métodos de lógica de predicado. Por ejemplo, no puede representar la información de que Fido es un gato o un perro, ni puede representar información relacional como: Si esta planta es más alta que esa planta, entonces también es más antigua.