7.6: CONCLUSIONES
- Page ID
- 84336
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
El diseño exitoso de amplificadores de acoplamiento directo de baja deriva depende de la explotación de las propiedades de seguimiento únicas del amplificador diferencial y de la aplicación de una serie de trucos de reducción de deriva que han evolucionado. En vista de las muchas trampas posibles, es tranquilizador darse cuenta de que la deriva de varios amplificadores operacionales de circuito integrado disponibles comercialmente es del orden de 3\(\mu V\) por grado centígrado o inferior, y que al menos un diseño de componentes discretos logra una deriva de 0.5\(\mu V\) por grado Centi grado.
El propósito de las derivaciones y ejemplos simples pero algo tediosos de esta sección no ha sido permitir una evaluación exacta de la deriva de un circuito, sino enfatizar que “las pequeñas cosas significan mucho”, e indicar las fuentes dominantes de deriva de un diseño particular para que se reduzcan.
PROBLEMAS
Ejercicio\(\PageIndex{1}\)
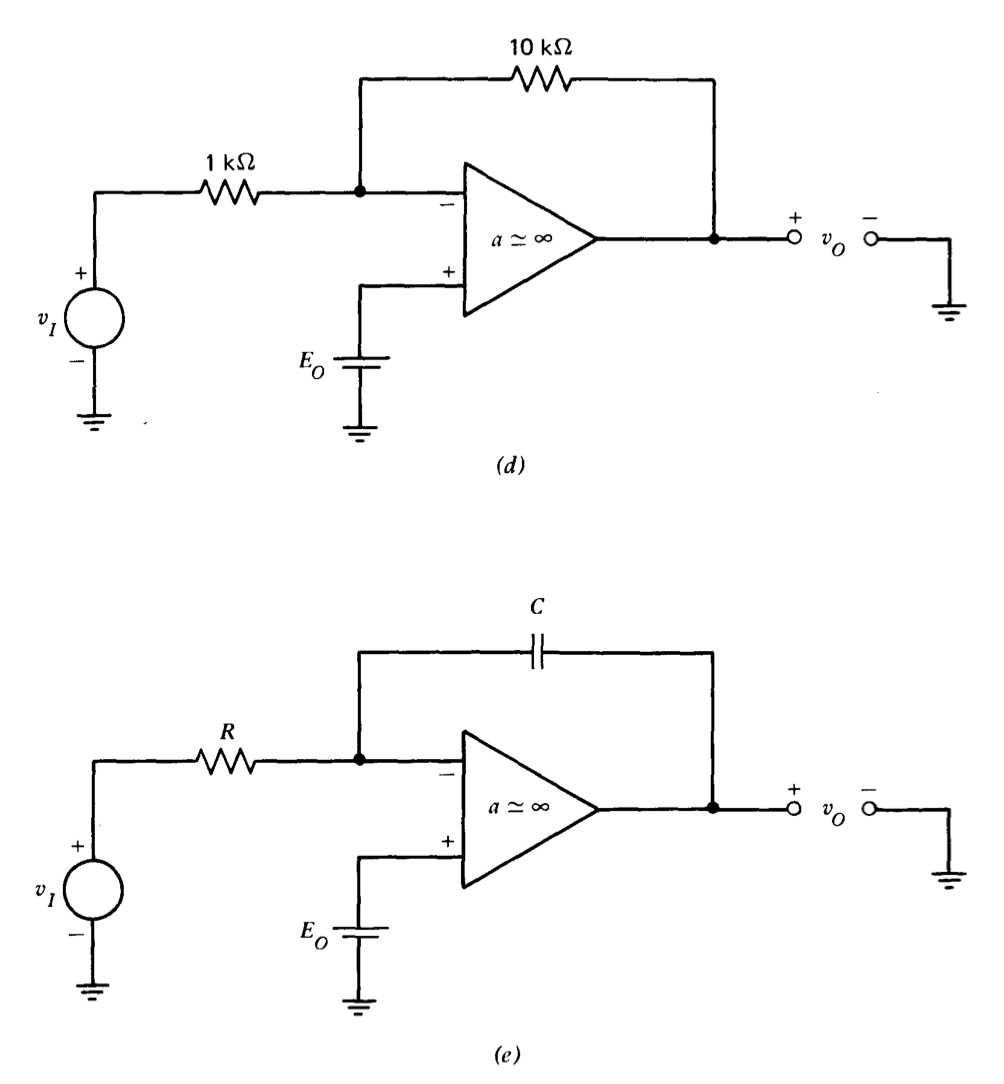
La Figura 7.23 muestra varias conexiones de amplificación que consisten en amplificadores ideales y componentes pasivos. Las fuentes de compensación se muestran como baterías. Calcular el desplazamiento referido a la entrada (el voltaje de entrada requerido para realizar\(v_O = 0\)), el desplazamiento de salida (el voltaje de salida con\(v_I = 0\)), y la ganancia\((v_o /v_i)\) para cada conexión.
Ejercicio\(\PageIndex{2}\)
Considerar un amplificador operacional con un valor particular de desplazamiento\(E_O\) referido a su entrada. Compare el desplazamiento referido a la entrada de conexiones de amplificador que combinan este amplificador con componentes pasivos para provide ganancias inversoras o no inversoras con una magnitud de\(A\).
Ejercicio\(\PageIndex{3}\)
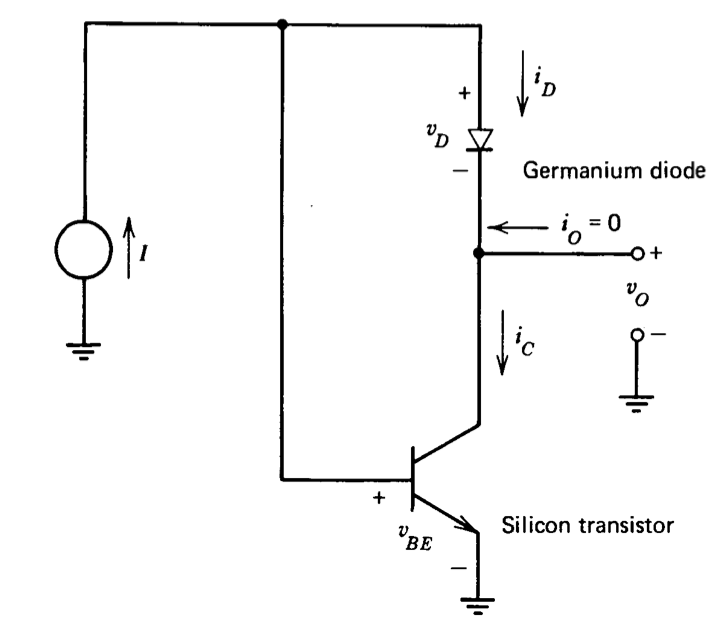
La Figura 7.24 muestra un circuito que puede proporcionar una tensión de salida independiente de la temperatura. Supongamos que el transistor tiene muy alto\(\beta\) y eso\(i_O = 0\). Las variables de diodo se relacionan como
\[i_D = A_d T^3 e^{q(v_D - 0.782)/kT} \nonumber \]
mientras que la relación del transistor es
\[i_C = A_t T^3 e^{q(v_{BE} - 1.205)/kT} \nonumber \]
a) ¿Para qué proporción de\(A_d\) a\(A_t\) hace\(\partial v_O/\partial T = 0\)?
b) ¿Qué es\(v_O\) con la condición de parte\(a\) satisfecha?
c) ¿Cuál es la resistencia de salida de esta conexión?
Ejercicio\(\PageIndex{4}\)
La relación corriente-voltaje para una familia de diodos se puede aproximar como
\[i_D = K e^{q(v_D - 1.2)/kT}\nonumber \]
donde\(K\) es una constante (independiente de la temperatura) que puede variar de diodo a diodo.
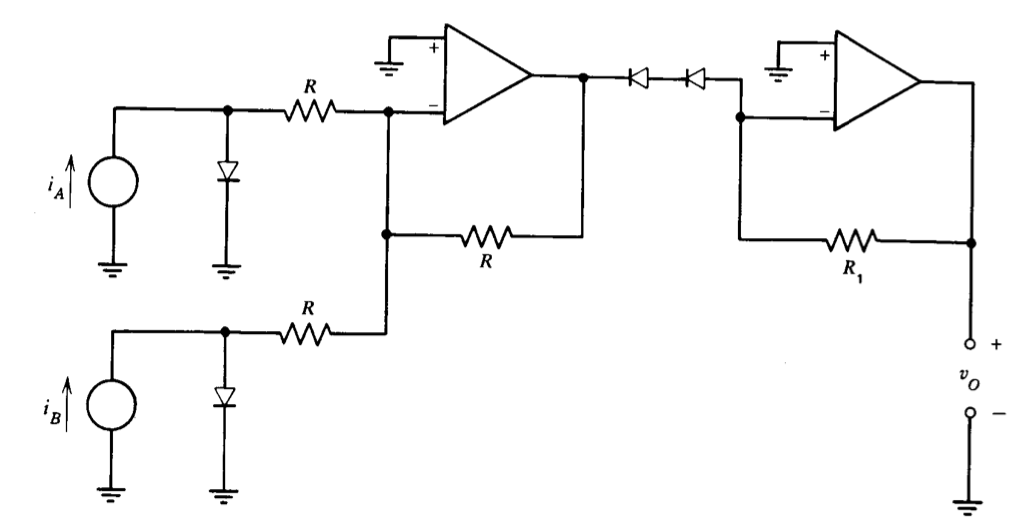
(a) Cuatro de estos diodos con valores idénticos para\(K\) están conectados como se muestra en la Figura 7.25. Encontrar\(v_O\) como una función si\(i_A\) y\(i_B\). Se puede suponer que las corrientes a través de todas las resistencias\(R\) son mucho más pequeñas que\(i_A\) o\(i_B\) y que ambos amplificadores operativos son ideales.
b) Determinar una expresión para
\[\dfrac{\partial v_D}{\partial T} |_{i_D = \text{const}} \text{ for these diodes.}\nonumber \]
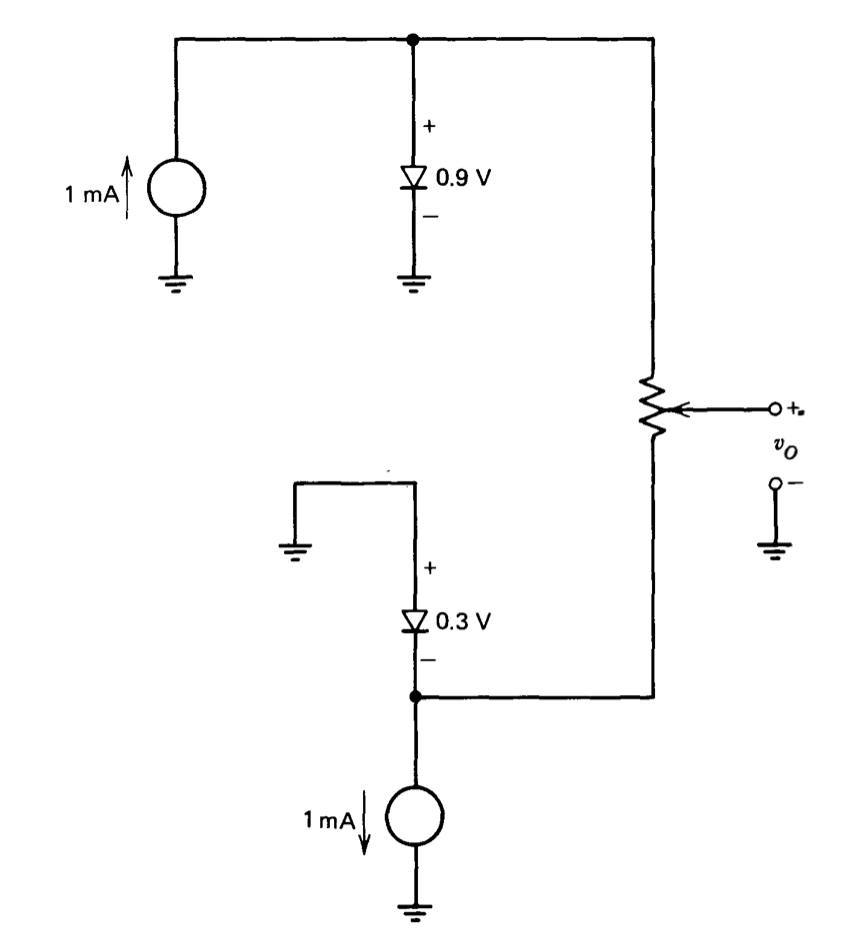
c) Supongamos que, debido al control increíblemente deficiente del proceso utilizado para hacer estos diodos, es posible encontrar dos diodos que, a\(T = 300^{\circ} K\) y\(1\ mA\) de corriente directa, tengan voltajes directos de 0.3\(V\) y 0.9\(V\), respectivamente. Estos diodos están conectados como se muestra en la Figura 7.26, y el pot se ajusta de manera que\(\partial v_O/\partial T = 0\). ¿Qué es vo con este ajuste de olla?
Ejercicio\(\PageIndex{5}\)
La relación corriente-voltaje para un diodo particular es
\[i_D = AT^{2.5} e^{q(v_D - 1.205)/kT}\nonumber \]
El valor de la constante\(A\) es tal que en\(300^{\circ} K\) y\(v_D = 0.6\ V\),\(i_D = 1\ mA\).
a) Determinar\(\dfrac{\partial v_D}{\partial T} |_{i_D = \text{const}}\)
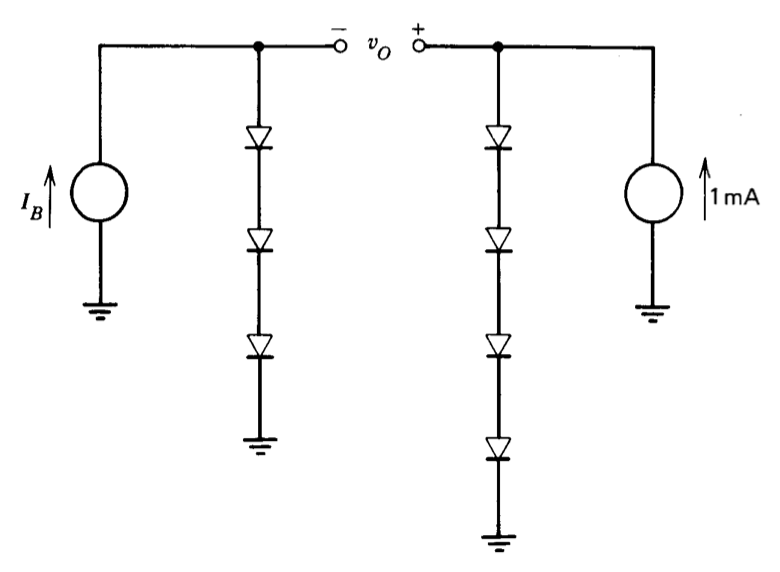
(b) Siete diodos idénticos están conectados como se muestra en la Figura 7.27. Mediante la elección apropiada de\(i_B\), es posible hacer que la temperatura de vo sea independiente en un rango limitado de temperatura. Determinar el valor requerido de\(v_O\) para que
\[\dfrac{\partial v_O}{\partial T} |_{i_B = \text{const}} = 0 \ \ \ \text{ at } T = 300^{\circ} K\nonumber \]
Aproximar el valor de\(I_B\) necesario para obtener el valor requerido de\(v_O\).
(c) Calcular la segunda derivada de vo con respecto a la temperatura. Utilice este valor para estimar el rango de temperatura sobre el cual\(v_O\) permanece dentro de una parte\(10^5\) de su\(300^{\circ} K\) valor.
(d) Repetir parte\(b\) asumiendo que la magnitud de la fuente de corriente de la derecha se incrementa a\(10\ mA\).
El tipo de referencia de voltaje que resulta de esta topología se denomina referencia de banda prohibida. El principio subyacente se utiliza como referencia de voltaje en varios circuitos integrados disponibles.
Ejercicio\(\PageIndex{6}\)
Se construye un amplificador diferencial con la topología mostrada en la Figura 7.11, con la excepción de que también se pueden aplicar señales a la base del transistor derecho. El valor de la fuente de corriente es 20\(\mu A\), y la resistencia incre de salida mental de este elemento es 10\(M\Omega\). (Las razones de la resistencia finita de salida de las fuentes de corriente se discuten en la Sección 8.3.5.) Cal culate la relación de rechazo de modo común de este amplificador como una función del desequilibrio fraccional en las resistencias de carga del colector\(\Delta\), asumiendo que todos los parámetros del transistor están perfectamente adaptados.
Ejercicio\(\PageIndex{7}\)
Un amplificador operacional se construye usando una etapa de entrada diferencial de transistor bipolar. Se encuentra que cuando la entrada inversora del amplificador está puesta a tierra, la tensión de salida del amplificador es cero\(25^{\circ} C\) cuando se aplica una tensión positiva de magnitud\(\Delta V\) a la entrada no inversora del amplificador. Usted puede suponer que este desplazamiento y cualquier deriva dependiente de la temperatura del amplificador operacional son causados solamente por una falta de coincidencia entre las cantidades\(I_S\) del par entrada-transistor, y que las variables del transistor están relacionadas por la Ecuación 7.2.1.
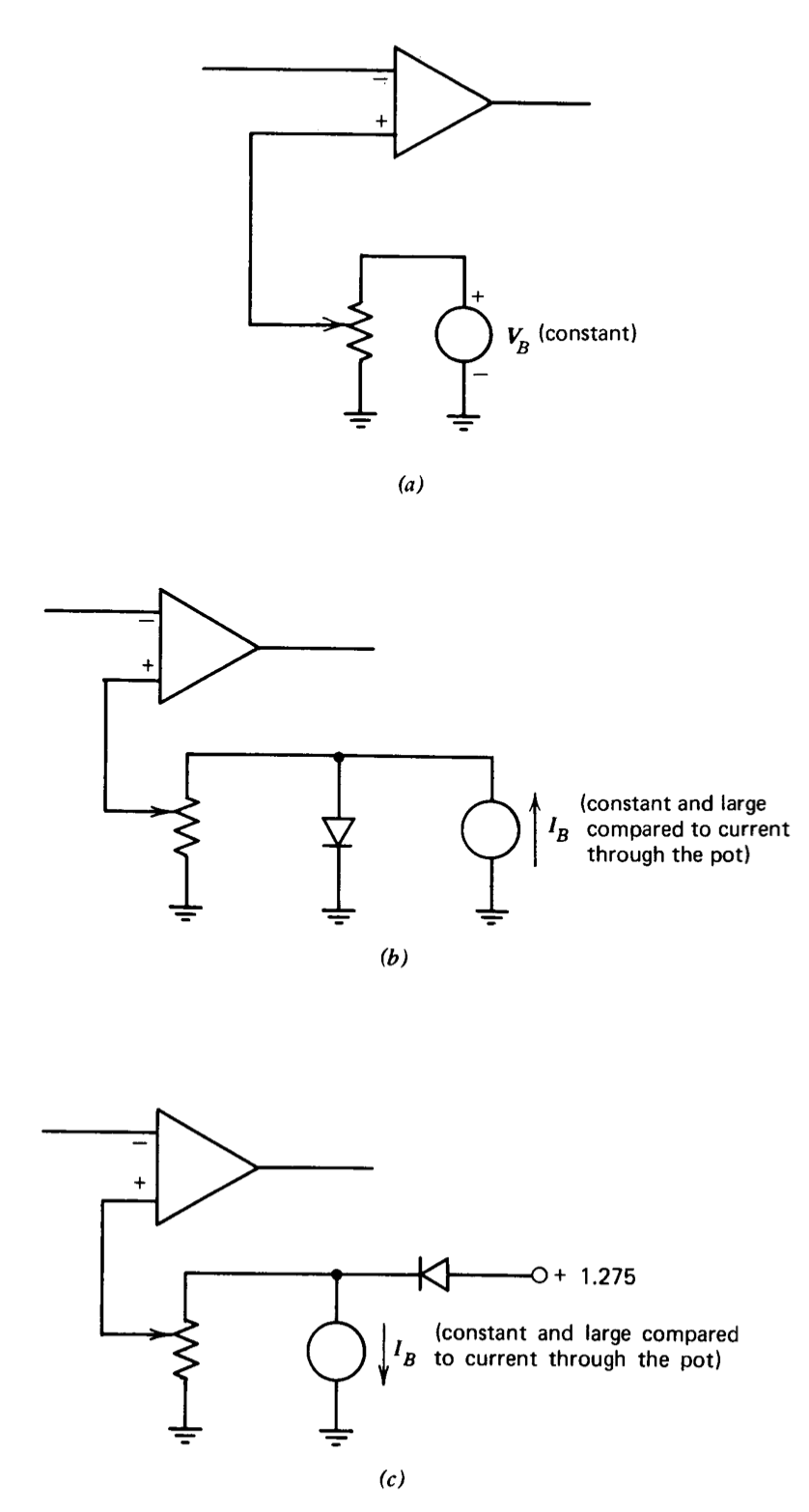
El amplificador operacional está diseñado para su uso en una conexión de amplificador inversor y, por lo tanto, es posible reducir el desplazamiento efectivo en la entrada inversora a cero\(25^{\circ} C\) al aplicar un voltaje\(\Delta V\) a la entrada no inversora. Tres técnicas para obtener este voltaje de polarización se indican en la Figura 7.28. Comente sobre la efectividad de estos tres métodos de equilibrio en la reducción de la deriva de temperatura del amplificador. Supongamos que el diodo
la variación de voltaje directo con la temperatura viene dada por
\[\dfrac{\partial v_D}{\partial T} |_{i_D = \text{const}} = \dfrac{(v_D - V_{go})}{T} - \dfrac{3k}{q}\nonumber \]
en partes\(b\) y\(c\).
Ejercicio\(\PageIndex{8}\)
Se construye y equilibra un amplificador diferencial como se muestra en la Figura 7.10. Después del equilibrio, se encuentra que el transistor\(Q_1\) está operando a una corriente de colector quiescente de\(1.1\ mA\), mientras que\(Q_2\) opera en un colector cur renta de\(0.9\ mA\). Los transistores utilizados son dispositivos discretos montados en una proximidad térmica razonablemente cercana, y tienen una resistencia térmica diferencial de\(20^{\circ} C\) por vatio (es decir, si un miembro del par opera a un nivel de potencia\(\Delta P\) vatios por encima del del otro, su temperatura es\(20 \times \Delta P\) grados centígrados superior). Estimar el desplazamiento referido a la entrada que resulta para un cambio de un voltio en el voltaje de la fuente de alimentación.
Ejercicio\(\PageIndex{9}\)
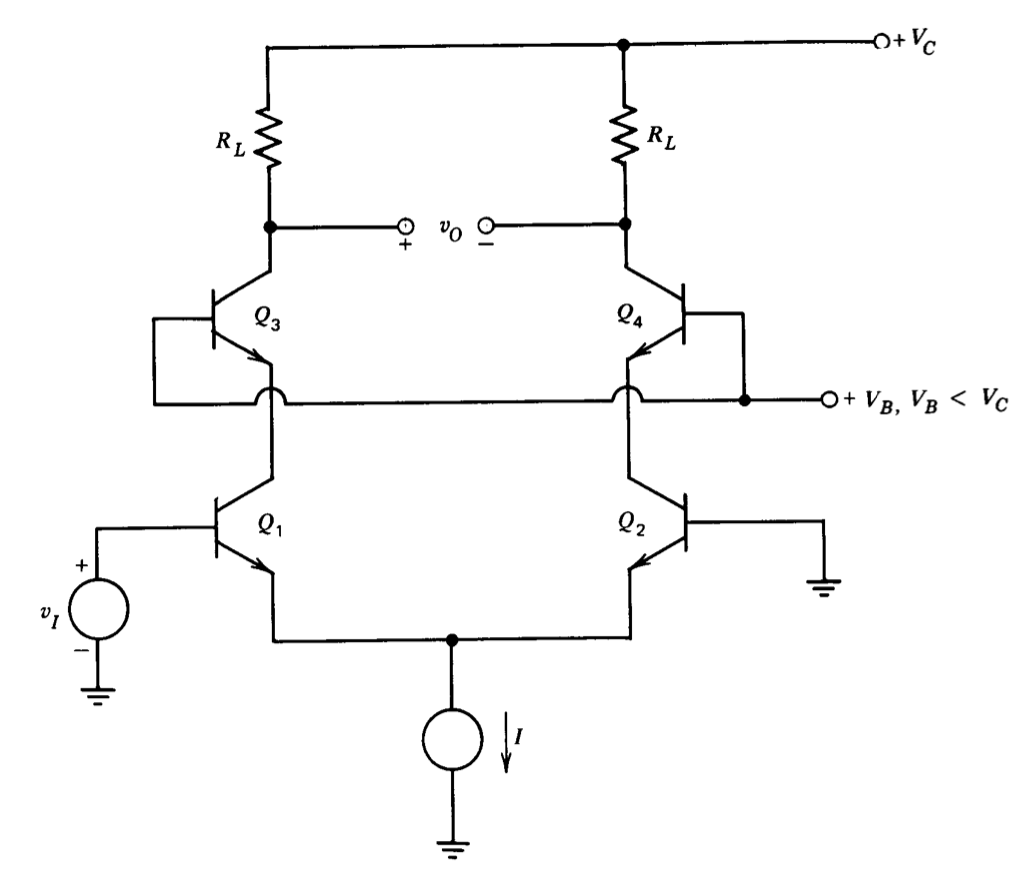
En la Figura 7.29 se muestra un amplificador diferencial que puede proporcionar una capacitancia de entrada baja y\(V_B\), mediante un control adecuado del voltaje de polarización, una alta relación de rechazo en modo común. Asumir eso\(Q_1\) y\(Q_2\) están perfectamente emparejados. Asumir además que\(\beta_3 = \beta_4 = 100\) en\(25^{\circ} C\). El voltaje de salida es entonces cero para\(v_I = 0\). Supongamos que el cambio fraccional en\(\beta_3\) es de 0.5% por grado Centi grado, mientras que el de\(\beta_4\) es 1% por grado Centígrado. Calcular el desplazamiento referido a la entrada para un cambio de\(1^{\circ} C\) temperatura.
Ejercicio\(\PageIndex{10}\)
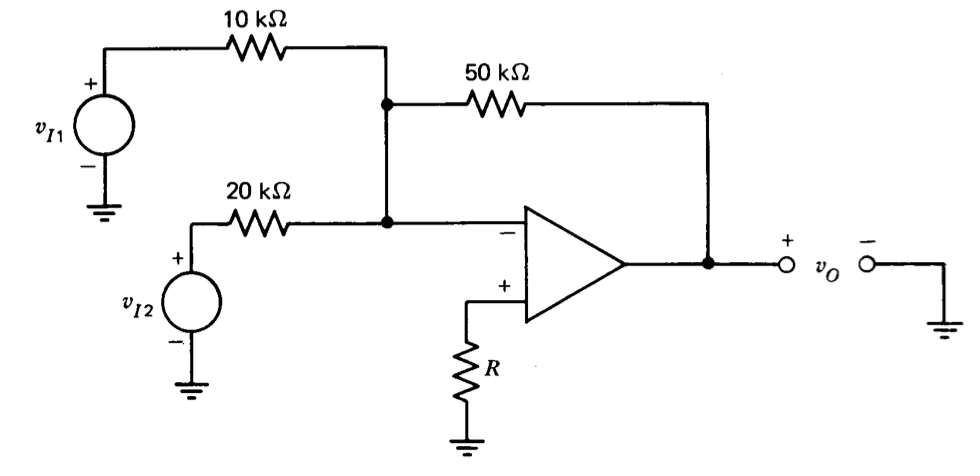
Se encuentra que un amplificador operacional tiene un requisito de corriente de polarización en su entrada no inversora que es 10% más alto que el de su entrada inversora a todas las temperaturas de interés. El amplificador está conectado como se muestra en la Figura 7.30. Seleccione el valor\(R\) que minimiza el efecto de la corriente de entrada en el rendimiento del circuito.
Ejercicio\(\PageIndex{11}\)
Se encuentra que la corriente en la entrada inversora de un cierto amplificador operacional es igual a\(10^{-3}A/T^2\) donde\(T\) esta la temperatura en grados Kelvin. El amplificador se va a utilizar en una conexión inversora; en consecuencia, la técnica ilustrada en la Figura 7.15 puede emplearse para la compensación de corriente de entrada. Los parámetros se seleccionan para que el diodo opere a una manera casi constante\(1\ mA\), y su voltaje directo a\(300^{\circ} K\) está\(600\ mV\) en esta corriente. Las características de corriente-voltaje del diodo son de la forma general
\[i_D = AT^3 e^{q(V_D - C_{go})/kT}\nonumber \]
Seleccione la resistencia\(R_2\) y la fuente de polarización\(V_A\) en la Figura 7.15 para que la corriente de entrada y su derivada con respecto a la temperatura se cancelen en\(300^{\circ} K\). ¿Cuál es la corriente de entrada máxima compensada en el rango de temperatura de 250 para\(350^{\circ} K\) usar esta forma de compensación? Contraste este rango con la cantidad correspondiente obtenida sin compensación y cancelando la corriente de entrada a\(300^{\circ} K\) con una corriente de polarización fija.
Ejercicio\(\PageIndex{12}\)
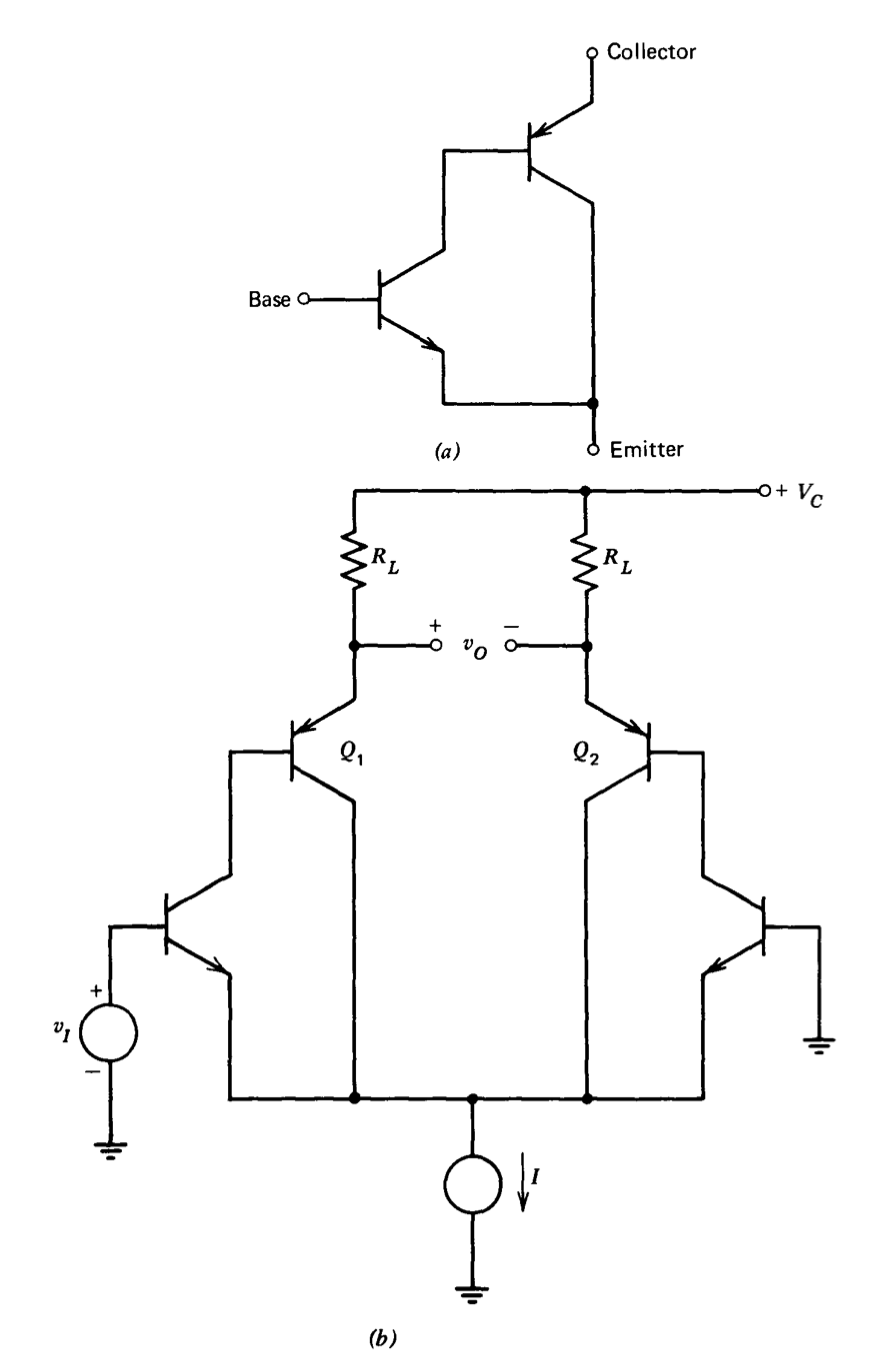
El uso de transistores de etapa de entrada conectados a Darlington se discute en la Sección 7.4.4. Una conexión alternativa de alta ganancia es la conexión Darlington complementaria que se muestra en la Figura 7.31\(a\). Un amplificador diferencial que emplea esta conexión se muestra en la Figura 7.31\(b\). Determinar la deriva de voltaje de esta conexión en función de los cambios relativos de ganancia de corriente del\(Q_1-Q_2\) par mediante un argumento similar al utilizado para la Figura 7.20.
Ejercicio\(\PageIndex{13}\)
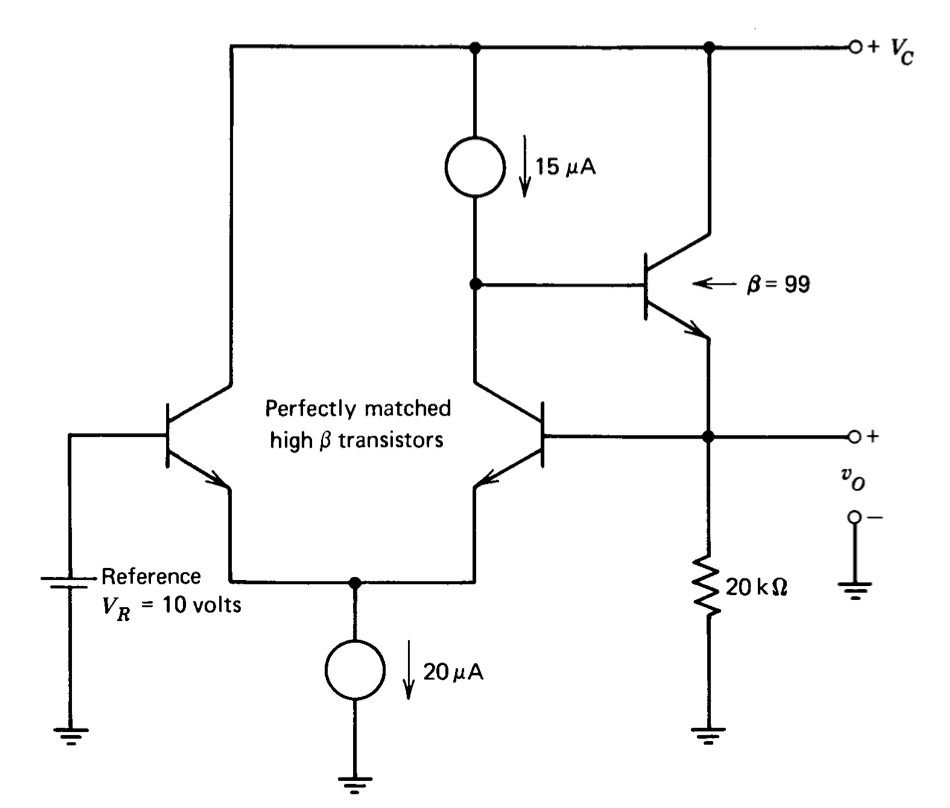
Se construye una fuente de alimentación regulada como se muestra en la Figura 7.32. Este suministro utiliza retroalimentación alrededor de un amplificador d-c muy simple en un intento de hacer\(v_O = V_R\).
(a) Determine el voltaje de salida para los valores del circuito como se muestra.
(b) ¿Cuánto cambia el voltaje de salida por un pequeño cambio fraccional en la ganancia de corriente de\(Q_2\)?
(c) Sugerir una modificación de circuito que reduzca la\(v_O\) dependencia del cambio fraccionario en\(\beta_2\).


