11.2: ESPECIFICACIONES

Es necesario comprender firmemente algunas de las especificaciones utilizadas para describir los amplificadores operativos para determinar si un amplificador será satisfactorio en una aplicación prevista. Desafortunadamente, especificando completamente un

circuito complejo es una tarea prácticamente imposible. El problema se ve agravado por el hecho de que no todos los fabricantes especifican las mismas cantidades, y no todos son igualmente conservadores con sus definiciones de “típico”, “máximo” y “mínimo”. En consecuencia, la cuestión de mayor interés para el de firmante (¿funcionará en mi circuito?) a menudo no tiene respuesta.

Definiciones

Algunas de las especificaciones más comunes y sus definiciones generalmente aceptadas se enumeran a continuación. Dado que hay una serie de amplificadores operativos disponibles que no están diseñados para el funcionamiento diferencial (por ejemplo, los amplificadores que usan compensación de alimentación directa son normalmente amplificadores de entrada única), las diferencias en las especificaciones entre los amplificadores de entrada diferencial y única se indican cuando aplicable.

Voltaje compensado de entrada. El voltaje que se debe aplicar entre las entradas de un amplificador de entrada diferencial, o entre la entrada y tierra de un amplificador de entrada única, para hacer que el voltaje de salida sea cero. Esta cantidad puede especificarse en un rango de temperatura dado, o se puede dar su cambio incremental (deriva) en función de la temperatura, el tiempo, la tensión de suministro o algún otro parámetro.

Corriente de polarización de entrada. La corriente requerida en la entrada de un amplificador de entrada única, o el promedio de las dos corrientes de entrada para un amplificador de entrada diferencial.

Corriente de compensación de entrada. La diferencia entre las dos corrientes de entrada de un amplificador de entrada diferencial. Tanto la corriente de compensación como la polarización se definen para el voltaje de salida cero, pero en la práctica la dependencia de estas cantidades en el nivel de voltaje de salida es mínima. A menudo se especifica la dependencia de estas cantidades de la temperatura u otras condiciones de operación.

Relación de rechazo en modo común. La relación entre la ganancia diferencial y la ganancia en modo común.

Sensibilidad a la tensión de alimentación. El cambio en el voltaje de compensación de entrada por unidad cambia en el voltaje de fuente de alimentación. El recíproco de esta cantidad se denomina relación de rechazo de voltaje de suministro.

Rango de entrada de modo común. El rango de señal de entrada de modo común para el cual un amplificador diferencial permanece lineal.

Rango diferencial de entrada. La señal diferencial máxima que se puede aplicar sin destruir el amplificador.

Rango de voltaje de salida. La señal de salida máxima que se puede obtener sin distorsión significativa. Esta cantidad generalmente se especifica para una resistencia de carga dada.

Resistencia de entrada. Las cantidades incrementales se especifican normalmente para señales diferenciales (entre entradas) y de modo común (ya sea de entrada a tierra).

Resistencia de salida. Cantidad incremental medida sin retroalimentación a menos que se especifique lo contrario.

Ganancia de voltaje o ganancia de bucle abierto. La relación del cambio en la salida del amplificador pone voltaje a su cambio en el voltaje de entrada cuando el amplificador está en su región lineal y cuando la señal de entrada varía extremadamente lentamente. Esta cantidad se especifica frecuentemente para un gran cambio en el nivel de voltaje de salida.

Tasa de giro. La tasa máxima de tiempo de cambio de voltaje de salida. Esta cantidad depende de la compensación para un amplificador compensado externamente. Alternativamente, se puede especificar la frecuencia máxima a la que se puede obtener una salida sinusoidal de amplitud dada no distorsionada.

Especificaciones de ancho de banda. La especificación más completa es una parcela de Bode, pero desafortunadamente no siempre se da una. Otras cantidades especificadas frecuentemente incluyen frecuencia de ganancia unitaria, tiempo de subida para una entrada de paso o frecuencia de media potencia para una conexión de retroalimentación dada. Lo más confuso es una especificación de producto de ganancia de ancho de banda, que puede ser la frecuencia de ganancia unitaria, o puede ser el producto de ganancia de voltaje de bucle cerrado y ancho de banda de media potencia en alguna conexión de retroalimentación.

Figura 11.1 Amplificador no inversor.

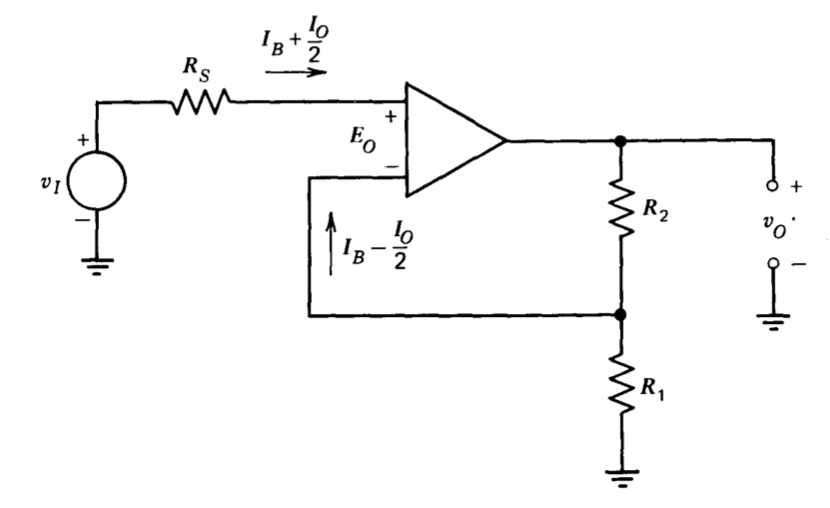
Incluso cuando las especificaciones del amplificador operacional se suministran honestamente y con un detalle razonable, la predicción del rendimiento de un amplificador en una conexión particular puede ser un proceso involucrado. Como ejemplo de este tipo de cálculo, considere el problema relativamente simple de encontrar la tensión de salida de la conexión del amplificador no inversor que se muestra en la Figura 11.1 cuando\(v_I = 0\). El desplazamiento de voltaje del amplificador es igual a\(E_O\). Se supone que la ganancia de voltaje de baja frecuencia del amplificador ao es muy grande de modo que el voltaje entre los terminales de entrada del amplificador es casi igual a\(E_O\). (Recordemos que con\(E_O\) aplicado a los terminales de entrada,\(v_O = 0\). Si\(a_0\) es muy grande, se puede obtener cualquier otra tensión de salida d-c dentro de la región lineal del amplificador con una tensión de aproximadamente\(E_O\) aplicada entre las entradas). Las corrientes en los terminales de entrada del amplificador expresadas en términos de la corriente de polarización\(I_B\) y la corriente\(I_O\) de compensación también se muestran en esta figura. (La especificación de las corrientes de entrada en términos de corriente de polarización y compensación no indica, por supuesto, qué corriente de terminal de entrada es mayor para un amplificador en particular. Se ha supuesto arbitrariamente en la Figura 11.1 que la corriente de compensación se suma a la corriente de polarización en la entrada no inversora y resta de ella en la entrada inversora).

Los valores de voltaje y corriente mostrados en la figura implican que, para\(v_I = 0\),

\[-R_S \left (I_B + \dfrac{I_O}{2} \right ) - v_O \left ( \dfrac{R_1}{R_1 + R_2} \right ) + \left (I_B - \dfrac{I_O}{2} \right ) \dfrac{R_1 R_2}{R_1 + R_2} = E_O \nonumber \]

Resolviendo\(V_O\) rendimientos

\[v_O = -\dfrac{(R_2 + R_1)}{R_1} E_O - \left (\dfrac{R_1 + R_2}{R_1} \right ) R_S \left (I_B + \dfrac{I_O}{2} \right ) + R_2 \left (I_B - \dfrac{I_O}{2} \right )\label{eq11.2.2} \]

Esta ecuación muestra que el voltaje de salida atribuible a la corriente de entrada del amplificador se puede reducir escalando los niveles de resistencia, pero que el error resultante del desplazamiento de voltaje es irreducible ya que la relación\((R_1 + R_2)/R_1\) presumiblemente debe seleccionarse sobre la base de la ganancia de bucle cerrado ideal requerida. La ecuación\(\ref{eq11.2.2}\) también demuestra el bien conocido resultado de que equilibrar las resistencias conectadas a las dos entradas elimina los desplazamientos atribuibles a la corriente de polarización de entrada, ya que con\(R_1 R_2/(R_1 + R_2) = R_S\), la tensión de salida es independiente de\(I_B\).

Como otro ejemplo del uso de especificaciones de amplificador, considere un dispositivo con un desplazamiento\(E_O\), una ganancia d-c de\(a_0\), y un voltaje de salida máximo\(V_{OM}\). El voltaje de entrada diferencial máximo requerido para obtener cualquier voltaje de salida estático dentro del rango dinámico del amplificador es entonces (Se supone que las cantidades en la ecuación son magnitudes máximas. La posibilidad de cancelación por signos algebraicos existe para una sola polaridad del voltaje de salida, y por lo tanto se ignora al calcular la magnitud máxima de la tensión de entrada.)

\[V_{IM} = E_O + \dfrac{V_{OM}}{a_0} \nonumber \]

Esta ecuación muestra que los valores de ao en exceso\(V_{OM}/E_O\) reducen el voltaje de entrada del amplificador (que debe ser bajo para que la ganancia de bucle cerrado se aproxime a su valor ideal) solo ligeramente. Concluimos que si\(a_0 > V_{OM}/E_O\), más esfuerzos de diseño de amplificadores operativos se dedican mejor a reducir el desplazamiento que a aumentar\(a_0\).

Medición de parámetros

Una forma de eludir la conspiración del silencio que a menudo rodea las especificaciones del amplificador es medir los parámetros que son importantes en una aplicación en particular. La medición permite al usuario determinar por sí mismo cómo un fabricante en particular define “típico”, “máximo” y “mínimo”, y también le permite nivelar circuitos para que las unidades superiores puedan ser utilizadas en las aplicaciones más exigentes.

Figura 11.2 Circuitos utilizados para determinar el voltaje de compensación y las corrientes de entrada. D.U.T. = Dispositivo bajo prueba. (\(a\)) Medición de voltaje compensado. (\(b\)) Medición de\(I_{-}\). (\(c\)) Medición de\(I_{+}\).

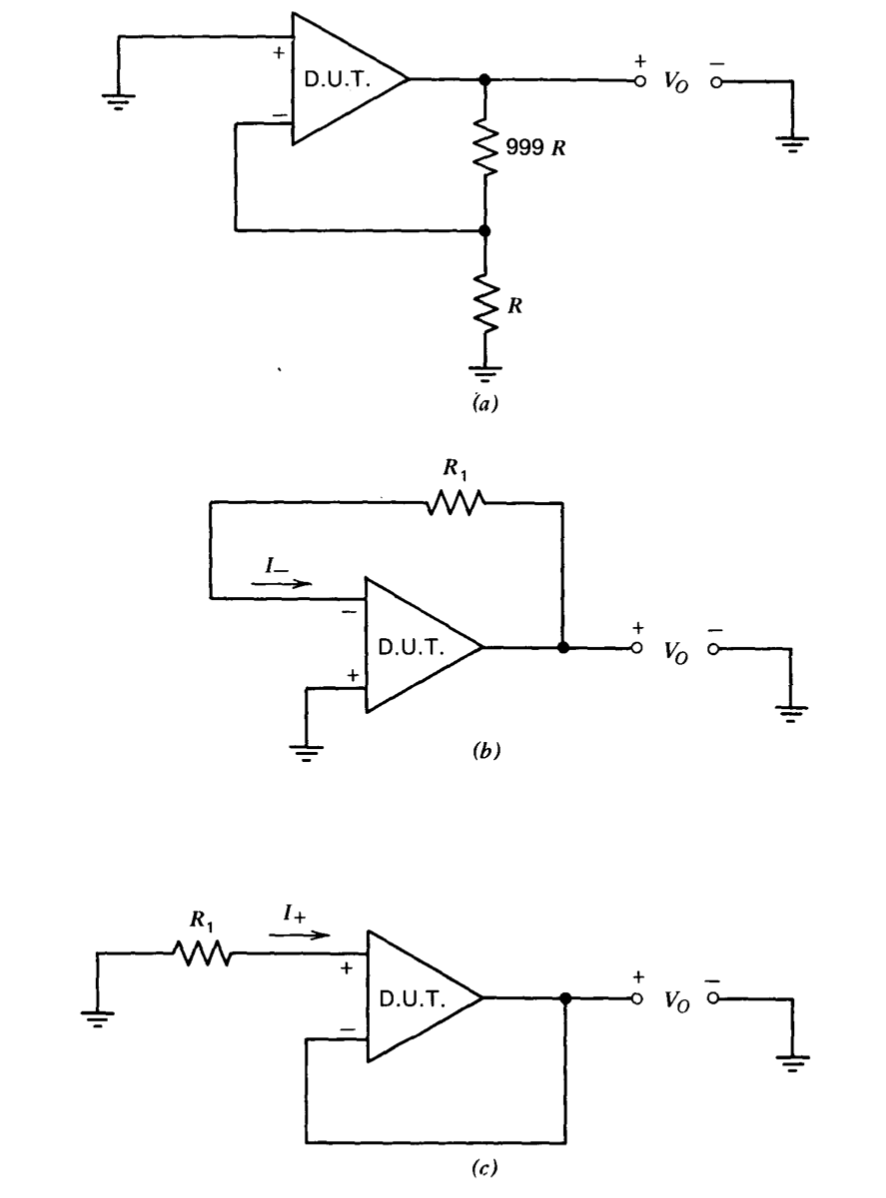
Las características d-c exclusivas de la ganancia de bucle abierto son relativamente sencillas de medir. Los circuitos que se pueden utilizar para medir el voltaje de compensación de entrada\(E_O\) y las corrientes de entrada en los dos terminales de entrada,\(I_{+}\) y\(I_{-}\), se muestran en la Figura 11.2. En el circuito de la Figura 11.2\(a\), supongamos que los valores de resistencia se eligen de manera que\(|E_O| gg |I_R|\). Los voltajes de reposo son

\[(-10^{-3} V_O + E_O)a_0 = V_O \nonumber \]

para una polaridad de referencia apropiadamente elegida para\(E_O\). Resolviendo esta ecuación para\(V_O\) rendimientos

\[V_O = \dfrac{a_0 E_O}{1 + 10^{-3} a_0} \simeq 10^3 E_O \nonumber \]

Así vemos que este circuito utiliza el amplificador para elevar su propio voltaje de compensación a un nivel fácilmente medido.

Si la resistencia\(R_1\) en las figuras 11.2\(b\) y 11.2\(c\) se elige de manera que ambas\(|I_{-} R_1|\) y\(|I_{+} R_1|\gg |E_O|\), las tensiones de salida sean

\[V_O = I_{-} R_1 \nonumber \]

y

\[V_O = -I_{+} R_1 \nonumber \]

respectivamente. La medición de\(I_{-}\) y\(I_{+}\) permite el cálculo directo de corrientes de compensación y polarización, ya que recordamos de definiciones anteriores que la corriente de polarización es igual al promedio de\(I_{+}\) y\(I_{-}\), mientras que la corriente de compensación es igual a la magnitud de la diferencia entre estas dos cantidades.

Se construye fácilmente una caja de prueba que incluye una toma para el dispositivo bajo prueba e incorpora conmutación de modo para seleccionar entre las pruebas. Los resultados se pueden mostrar en un movimiento económico del medidor D'Arsonval, ya que los valores de resistencia se pueden elegir para producir voltajes de salida del orden de un voltio. Las características de paso bajo del movimiento del medidor proporcionan un grado de rechazo de ruido que mejora la precisión de las mediciones. Si se requiere un filtrado de ruido adicional, se pueden usar condensadores de valor moderado en paralelo con las resistencias\(999R\) y\(R_1\) en la Figura 11.2.

Figura 11.3 Circuito de medición de desplazamiento con transmisión de bucle incrementada.

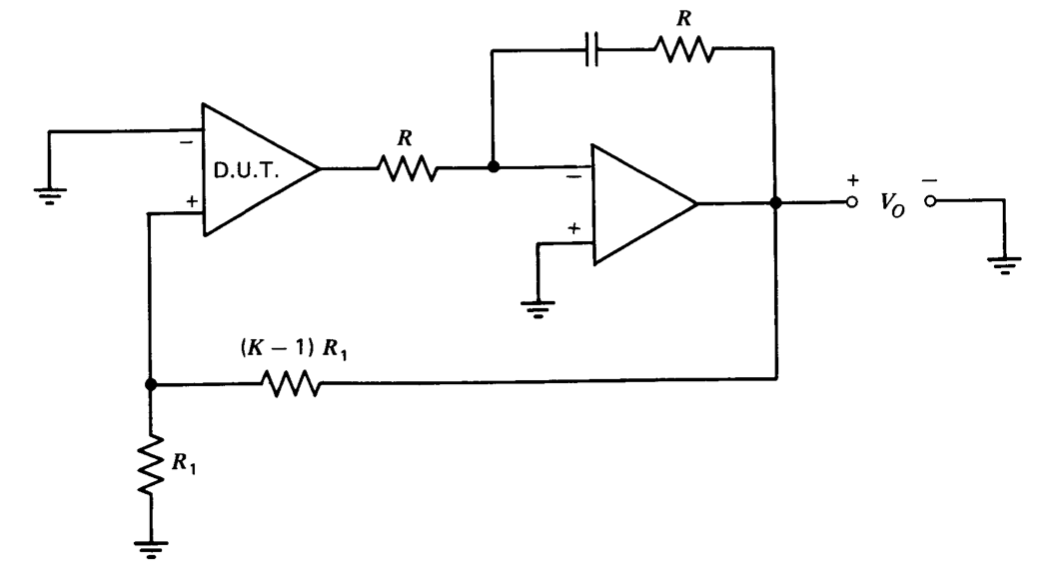
El circuito de medición de desplazamiento que se muestra en la Figura 11.2\(a\) requiere una gran magnitud de transmisión de bucle para un funcionamiento adecuado. Si existe la posibilidad de que la transmisión en bucle de baja frecuencia de un amplificador en particular sea demasiado pequeña, el circuito alternativo que se muestra en la Figura 11.3 se puede utilizar para medir el desplazamiento. El segundo amplificador proporciona una ganancia d-c muy grande con el resultado de que el voltaje fuera del amplificador bajo prueba es insignificante. A frecuencias moderadas, el segundo amplificador funciona como un inversor de ganancia unitaria para que la estabilidad del bucle no se vea comprometida por las características del integrador que resultan si\(R\) se elimina la resistencia de retroalimentación. Bajando el valor de este

la resistencia de retroalimentación con respecto a la resistencia de entrada del segundo amplificador puede mejorar la estabilidad, particularmente cuando la\((K - 1)R_1\) resistencia se desvía para reducir el ruido. Dado que esta conexión mantiene el voltaje de salida del amplificador bajo prueba cerca de tierra,\(V_O\) será (en ausencia de efectos de corriente de entrada) simplemente igual a\(KE_O\).

La relación de rechazo de voltaje de suministro de un amplificador se puede medir con la misma circuitería utilizada para medir la compensación si se incluye la provisión para variar los voltajes aplicados al amplificador. La relación de rechazo de voltaje de alimentación se define como la relación entre un cambio en el voltaje de suministro y el cambio resultante en el voltaje de compensación de entrada.

Figura 11.4 Circuito para medir la relación de rechazo en modo común.

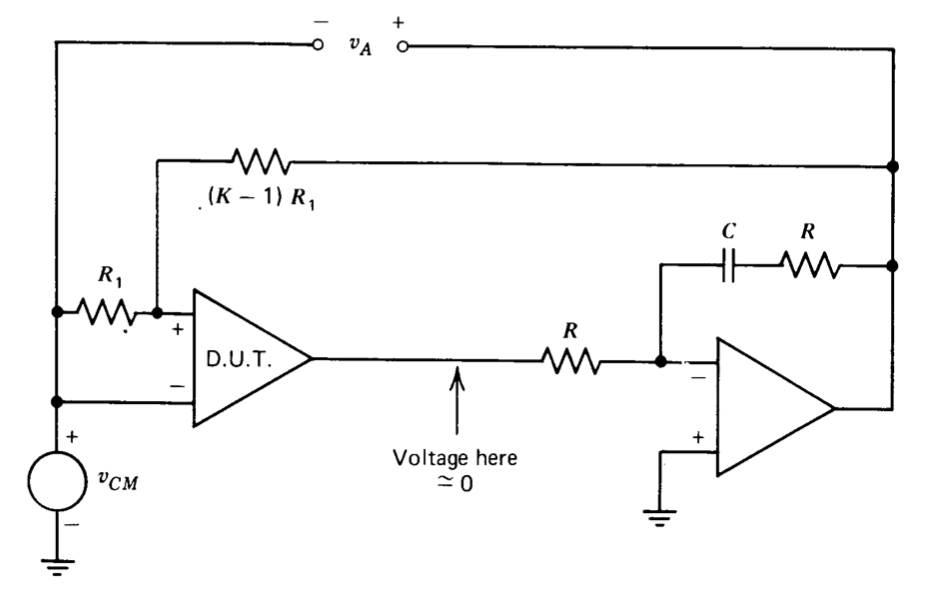
La técnica de incluir un segundo amplificador para aumentar la transmisión en bucle simplifica la medición de la relación de rechazo en modo común (ver Figura 11.4). Si la ganancia diferencial\(a_0\) del amplificador es grande en comparación con su ganancia de modo común\(a_{cm}\), podemos escribir

\[0 = a_{cm} v_{CM} + \dfrac{a_0 v_A}{K} \nonumber \]

Así

\ [\ izquierda |\ dfrac {a_0} {a_ {cm}}\ derecha | =\ texto {CMRR} =\ izquierda |\ dfrac {Kv_ {CM}} {v_a}\ derecha |

Dado que el voltaje\(v_A\) también incluye un componente proporcional al voltaje de compensación del amplificador, puede ser necesario usar mediciones incrementales para determinar con precisión la relación de rechazo.

La velocidad de respuesta de un amplificador puede depender de la tasa de cambio de tiempo del nivel de modo común de señal de entrada y será una función de compensación para un amplificador con compensación seleccionable. Los resultados estandarizados que permiten la intercomparación de varios amplificadores se pueden obtener conectando el amplificador como un inversor de ganancia unitaria y aplicando una entrada de paso que barre la salida del amplificador a través de la mayor parte de su rango dinámico. La sujeción de diodos en la entrada inversora del amplificador se puede utilizar para evitar grandes señales de modo común. (Ver Sección 13.3.7 para un circuito representativo.) Alternativamente, la tasa de respuesta máxima en una conexión específica de interés a menudo se puede determinar aplicando una señal de entrada lo suficientemente grande como para forzar la tasa de tiempo máxima de cambio de la tensión de salida del amplificador.

La función de transferencia de bucle abierto de un amplificador es considerablemente más difícil de medir. Consideremos, por ejemplo, el problema de determinar la ganancia d-c. Podríamos suponer ingenuamente que el amplificador podría operarse en bucle abierto (después de todo, estamos midiendo la ganancia de bucle abierto), sesgado en su región lineal aplicando un nivel de reposo de entrada apropiado, y la ganancia determinada agregando un paso incremental en la entrada y midiendo el cambio en el nivel de salida. Los peligros de este enfoque son legión. La señal de salida normalmente está dañada por el ruido y la deriva, por lo que los cambios son difíciles de determinar con precisión. También podemos encontrar que el amplificador exhibe un comportamiento biestable, y que no es posible encontrar un valor para la tensión de entrada que fuerce la salida del amplificador a su región lineal. Este fenómeno es el resultado de la retroalimentación térmica positiva en un circuito integrado, y también puede ocurrir en diseños discretos debido al autocalentamiento, retroalimentación a través de redes de polarización compartida o fuentes de alimentación, o por otras razones. La retroalimentación positiva

que lleva a que este comportamiento se vea inundado por la retroalimentación negativa aplicada alrededor del amplificador en aplicaciones normales, y por lo tanto no perturbe el rendimiento en las conexiones habituales.

Después de cierta frustración se suele concluir que se pueden obtener mejores resultados operando el amplificador en una conexión de bucle cerrado. Las amplitudes de señal se pueden ajustar para la salida más grande que asegura el rendimiento lineal a alguna frecuencia, y se mide la señal de entrada correspondiente. La magnitud y el ángulo de la función de transferencia se pueden obtener si la señal de entrada se puede determinar con precisión. Desafortunadamente, la señal en la entrada del amplificador suele ser ruidosa, particularmente en frecuencias donde la magnitud de ganancia de bucle abierto es grande. Un analizador de ondas o un amplificador seguido de un demodulador sensible a la fase accionado a la frecuencia de entrada puede ser necesario para mediciones precisas. Esta técnica puede incluso ser utilizada para determinar\(a_0\) si el amplificador está compensado de manera que el primer polo en su función de transferencia de bucle abierto esté ubicado dentro del rango de frecuencia del detector.

También hay métodos indirectos que se pueden utilizar para aproximar la función de transferencia de bucle abierto del amplificador. La frecuencia de bucle cerrado de señal pequeña o la respuesta transitoria se pueden medir para varios valores diferentes de retroalimentación independiente de la frecuencia\(f_0\). Una gráfica Nichols o las curvas de la Figura 4.26 pueden entonces ser utilizadas para determinar características importantes de\(a(j\omega )\) a frecuencias cercanas a aquella para la cual\(|a(j\omega )f_0 = 1\). Dado que se utilizan diversos valores offo, se\(a(j\omega )\) pueden determinar a varias frecuencias diferentes. Este tipo de medición a menudo arroja suficiente información para su uso en los cálculos de estabilidad.

Figura 11.5 Conexión para medir la función de transferencia de bucle abierto.

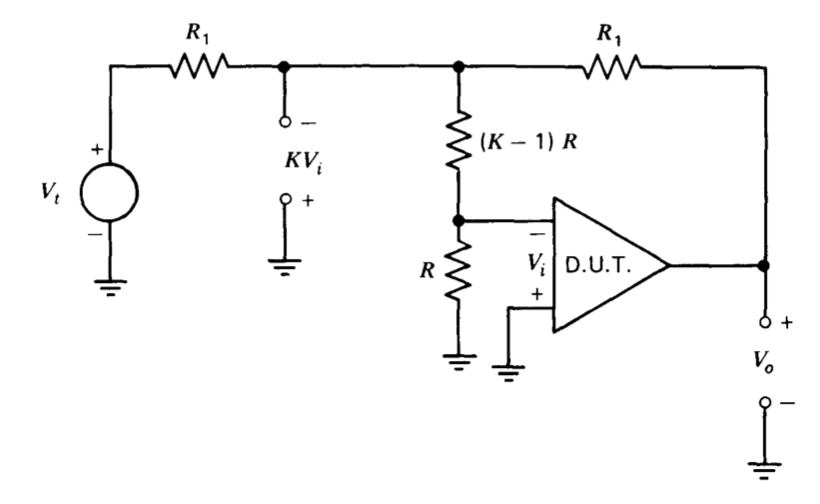
Una tercera posibilidad es probar el amplificador en una conexión que proporcione un múltiplo de la señal en la entrada del amplificador, de la misma manera que lo hace el circuito sugerido anteriormente para la medición de offset. La figura 11.5 muestra una posibilidad. La señal en la unión de las dos resistencias etiquetadas\(R_1\) es\(K\) veces tan grande como la señal de entrada aplicada al amplificador, y se puede comparar con cualquiera\(V_o\) o\(V_t\) (que es igual a\(-V\), cuando la transmisión en bucle es grande) para determinar el bucle abierto función de transferencia del amplificador. Tenga en cuenta que si se compara la señal en la unión de las dos resistencias de igual valor\(V_o\), este método no depende de la transmisión de bucle grande.

Si bien este método escala la señal de entrada, no proporciona filtrado, con el resultado de que puede ser necesario algún procesamiento adicional de la señal para mejorar la relación señal/ruido.