12.5: MÁS EJEMPLOS
- Page ID
- 84120
Se mencionó en la introducción al Capítulo 11 que el objetivo de la parte de aplicación de este libro era ilustrar conceptos para el diseño más que proporcionar ejemplos específicos y detallados con la esperanza generalmente inútil de que el lector pudiera aplicarlos directamente a sus propios problemas. El diseño exitoso casi siempre implica combinar bits y piezas, un concepto aquí, una topología allí, para finalmente llegar a la solución óptima. En esta sección veremos cómo algunas de las ideas introducidas anteriormente se combinan en configuraciones relativamente más sofisticadas. Los tres ejemplos que se presentan son todos “del mundo real” en el sentido de que reflejan requisitos reales que el autor ha encontrado recientemente en su propia obra.
Desfasador independiente de la frecuencia
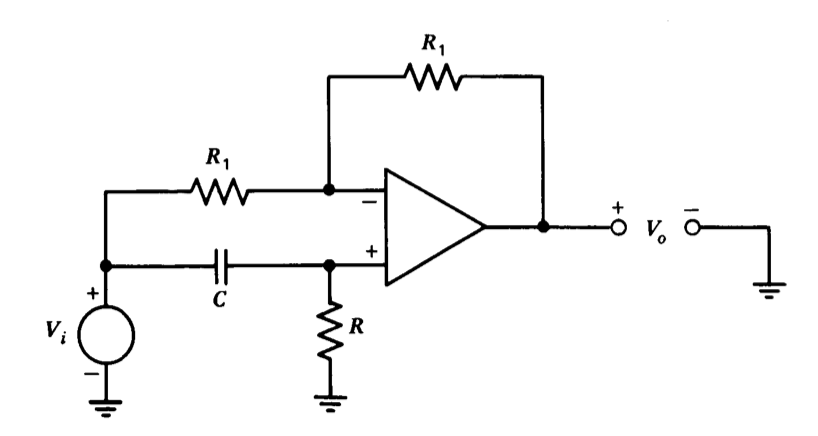
Hay una serie de conexiones operacional-amplificador, como la aproximación a un retardo de tiempo descrito en la sección anterior, que tienen una magnitud de función de transferencia independiente de la frecuencia combinada con características de fase especificadas. El desfasador mostrado en la Figura 12.30 es otro ejemplo de este tipo de circuitos. Reconocemos este circuito como una conexión de amplificador diferencial, y así nos damos cuenta de que su función de transferencia es
\[\dfrac{V_o (s)}{V_i (s)} = \left (\dfrac{2RCs }{RCs + 1} - 1 \right ) = \dfrac{RCs - 1}{RCs + 1} \nonumber \]
Esta función de transferencia (que es el negativo de un Pade de primer orden aproximarse a un retardo de tiempo de\(2RC\) segundos) produce un desplazamiento de fase que varía de frecuencias\(-180^{\circ}\) bajas\(0^{\circ}\) a frecuencias altas. Si se utiliza un potenciómetro o un transistor de efecto de campo\(R\), el desplazamiento de fase se puede variar manual o electrónicamente.
Una técnica para convertir resolvedor (Un resolvedor es básicamente un transformador con un acoplamiento primario a secundario que se puede variar cambiando mecánicamente la alineación relativa de estos devanados. Este dispositivo se utiliza como un transductor de ángulo mecánico resistente y de alta precisión.) las señales a forma digital requieren que se aplique un desplazamiento de\(90^{\circ}\) fase fijo a una señal sinusoidal sin cambio en su amplitud. La frecuencia de la señal que se va a desplazar en fase puede cambiar en un poco por ciento. Desafortunadamente, no hay funciones de transferencia lineal finito-polinomial que combinen características de magnitud independientes de la frecuencia con un desplazamiento de fase constante de 900. Si bien existen funciones de aproximación sobre rangos de frecuencia restringidos, la constancia de desplazamiento de fase de minuto de arco requerida en esta aplicación impidió el uso de tales funciones. Observamos que dado que una clase muy específica de señales de entrada (sinusoides de frecuencia única) se va a aplicar al desfasador, la linealidad puede no ser una restricción necesaria. Los circuitos no lineales, a pesar de nuestra incapacidad para analizarlos sistemáticamente, suelen tener propiedades muy interesantes.
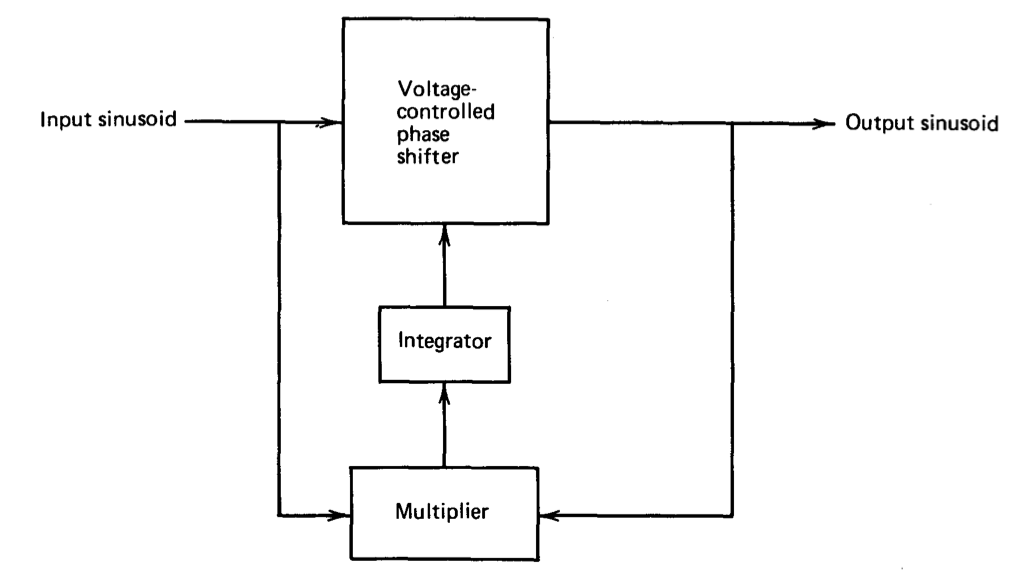
Considera la configuración mostrada diagramáticamente en la Figura 12.31 como una posible solución a nuestro problema. En este circuito, un desfasador de todos los pasos con una cantidad variable de voltaje de desplazamiento de fase es el elemento central. El circuito que se muestra en la Figura 12.30 con un transistor de efecto de campo utilizado para la resistencia\(R\) puede realizar esta función. El multiplicador se utiliza como detector de fase. Si la magnitud del desplazamiento de fase entre las señales de entrada y salida es menor que\(90^{\circ}\), el valor promedio de la salida del multiplicador será positivo, mientras que si esta magnitud está entre\(90^{\circ}\) y\(180^{\circ}\), la señal promedio de salida del multiplicador será negativa. El integrador, que proporciona el control
para el FET en el desfasador, filtra el segundo armónico que resulta de la multiplicación y suministra la ganancia de bucle necesaria para mantener el valor promedio de la salida del multiplicador en cero, forzando así un desplazamiento de fase 900 entre las señales de entrada y salida. Si bien el circuito descrito anteriormente puede resultar en una precisión moderada, una investigación detallada indicó que cumplir con las especificaciones requeridas probablemente no era práctico con esta topología.
Cabe señalar que si bien en este caso no se utilizó el enfoque básico descrito anteriormente, se trata de una técnica valiosa que tiene una serie de variaciones interesantes y útiles. Por ejemplo, el desplazamiento de fase de un filtro activo de paso alto o bajo de segundo orden es\(\pm 90^{\circ}\) cuando se excita en su frecuencia de esquina. Los filtros de seguimiento se pueden realizar reemplazando las resistencias fijas en un filtro activo por resistencias controladas por voltaje y usando una comparación de fases para ubicar la frecuencia de esquina del filtro en su frecuencia de excitación.
En algunas aplicaciones, se utilizan otros tipos de detectores de fase. Una posibilidad consiste en limitadores de alta ganancia que producen ondas cuadradas con cruce por cero sincronizadas con las de las ondas sinusoidales de interés. El ciclo de trabajo de una puerta OR exclusiva que opera sobre las ondas cuadradas indica la fase relativa de las señales originales.
El circuito anterior combinaba una red de paso completo que proporciona una magnitud de función de transferencia que es independiente de la frecuencia con retroalimentación que fuerza el desplazamiento\(90^{\circ}\) de fase a la frecuencia de operación. Un enfoque alternativo es combinar una red que proporciona desplazamiento\(90^{\circ}\) de fase en todas las frecuencias (un integrador) con retroalimentación que obliga a su magnitud de ganancia a ser una a la frecuencia de operación.
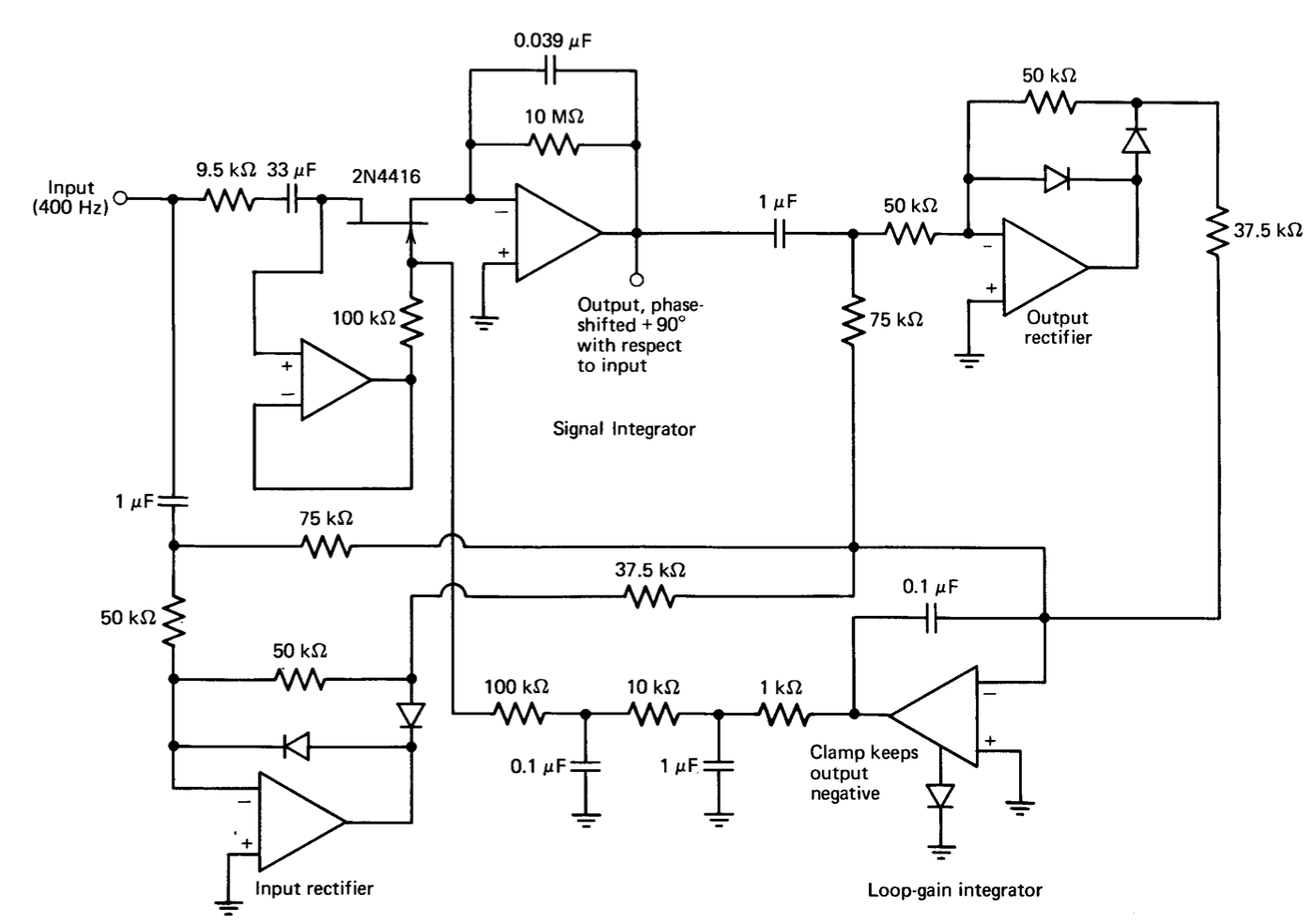
El circuito que evolucionó para implementar el concepto anterior se muestra en forma sólo ligeramente simplificada en la Figura 12.32. El integrador de señal proporciona los 90' requeridos de desplazamiento de fase. Su factor de escala se ajusta por medio del transistor de efecto campo para que se proporcione una magnitud de ganancia de uno a frecuencias cercanas al valor nominal de funcionamiento de 400 Hz. La mitad del voltaje drenaje-fuente del transistor de efecto campo se aplica a su puerta para linealizar la resistencia drenaje-fuente como se describe en la Sección 12.1.4. El amplificador de búfer de ganancia unitaria evita que la corriente que fluye a través de la red de puerta FET se integre. El condensador en serie con la resistencia de entrada del integrador de señal y la resistencia que deriva el condensador de integración son necesarios para evitar que este integrador se sature como consecuencia del desplazamiento del voltaje de entrada y la corriente de polarización. Si bien cambian el desplazamiento de fase ideal en un total de aproximadamente ocho minutos de arco, este valor se recorta junto con otros errores de desplazamiento de fase con una red (no mostrada) que sigue al integrador.
Las dos conexiones rectificadoras de precisión de onda completa se combinan con el integrador de ganancia de bucle para proporcionar una corriente promedio en el condensador de este integrador que es proporcional a la diferencia entre las magnitudes de las señales de entrada y salida. Si, por ejemplo, la magnitud de la señal de salida excede la magnitud de la señal de entrada, la tensión fuera del integrador de ganancia de bucle se acciona negativamente. Esta acción aumenta la resistencia incremental del FET, disminuyendo así el factor de escala del integrador de señal y disminuyendo la magnitud de la señal de salida. Las entradas a los rectificadores de precisión están acopladas a-c para que los componentes d-c de estas señales no influyan en las señales de salida del rectificador. Un filtro de paso bajo de dos polos sigue al integrador de ganancia de bucle para filtrar aún más armónicos que degradarían el rendimiento del integrador de señal.
El nivel de salida positivo máximo del integrador de ganancia de bucle se sujeta a través de un nodo interno a un nivel de salida máximo de cero voltios para eliminar un modo de enganche. Si este voltaje se volviera positivo, el FET conduciría la corriente de puerta, y esta corriente podría hacer que la salida del integrador de señal se saturara. Como resultado, se eliminaría el componente a-c de la salida del integrador de señal, y el bucle, en un intento de restaurar el equilibrio, impulsaría la salida del integrador de ganancia de bucle más positiva. La abrazadera de diodo impide el inicio de esta desafortunada cadena de eventos.
El circuito mostrado en la Figura 12.32 ha sido construido y probado a frecuencias de funcionamiento entre 395 y 405 Hz en el rango de temperatura de\(0^{\circ}\) a\(50^{\circ}\) Centígrados. (La retroalimentación también elimina los efectos de los cambios de valor de componente integrador de señal con la temperatura). Las amplitudes de señal de entrada y salida permanecen iguales dentro de I mV pico a pico en cualquier nivel de señal de entrada hasta 20 voltios pico a pico. El desplazamiento de fase del circuito con una entrada pico a pico de 20 voltios permanece constante dentro de un minuto de arco. Si bien el desplazamiento de fase real no es precisamente\(90^{\circ}\), el componente constante del error de fase se puede recortar como se describió anteriormente.
Moldeadora de Ondas Sinoidales
En las Secciones 6.3.3 y 12.2.1 se han discutido ciertos aspectos de un circuito generador de función que combina un integrador y un disparador Schmitt para producir ondas cuadradas y triangulares. Las versiones comerciales de este circuito generalmente también proporcionan una salida de onda sinusoidal que se sintetiza por el aparentemente improbable método de dar forma a la onda triangular con una red lineal por tramos. Esta técnica es práctica debido a la facilidad de generar ondas triangulares de frecuencia variable, y porque el uso de relativamente pocos segmentos en la red de conformación da sorprendentemente buena fidelidad de onda sinusoidal.
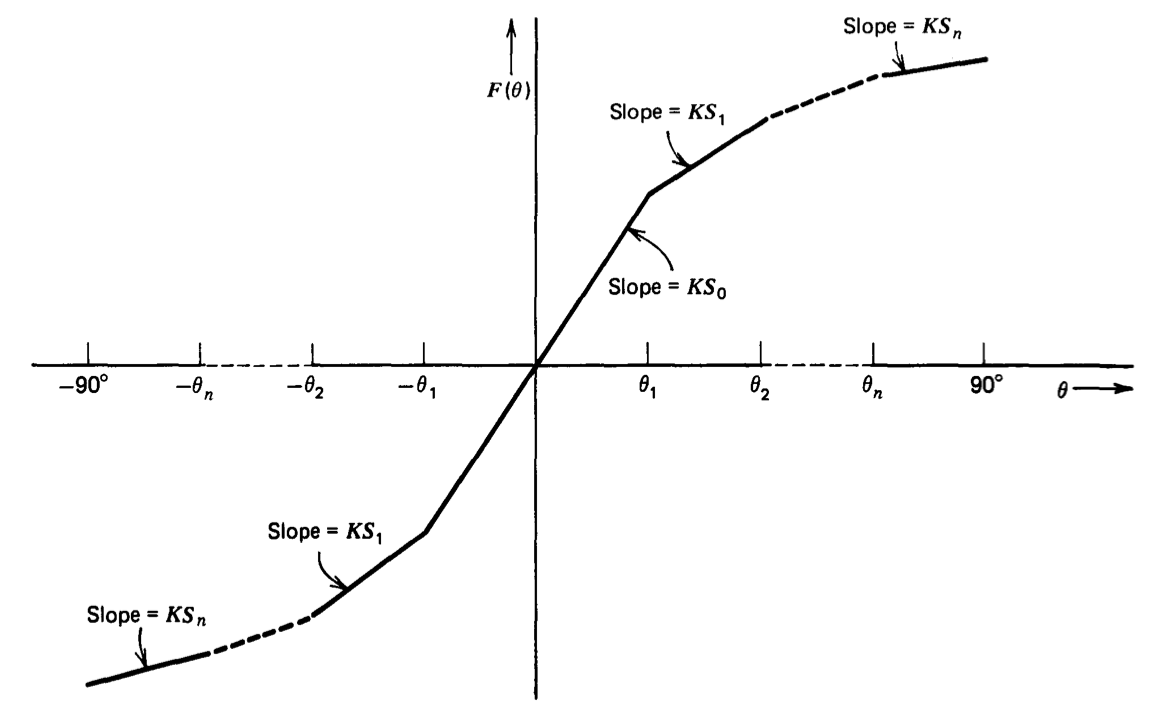
Parte del problema de diseño es determinar cómo deben elegirse las características de la red de conformación para aproximarse mejor a una onda sinusoidal. Los parámetros que definen la red se muestran en la Figura 12.33. Un total de n puntos de ruptura se ubican sobre el rango de variables de entrada de\(0^{\circ}\) a\(90^{\circ}\). El
pendiente de la relación de transferencia entrada-salida es\(KS_m\) entre\(\theta = \theta_m\) y\(\theta = \theta_{m+1}\). La constante multiplicadora\(K\) refleja el hecho de que solo las pendientes relativas son importantes, ya que un cambio multiplicativo en todas las pendientes cambia solo la magnitud de las características de transferencia de entrada-salida. La simetría de las características de transferencia sobre el origen asegura que la señal de salida no tendrá componente d-c y no contendrá armónicos pares cuando se utilice como entrada una señal triangular de valor promedio cero.
La especificación de red implica la elección de\(n\) valores de\(\theta\) (las ubicaciones de punto de interrupción) y pendientes\(n + 1\) relativas. Se puede demostrar que si se seleccionan los\(\theta\)'s de tal manera que
\[\theta_m = \dfrac{m 180^{\circ}}{2n + 1} \ \ \ 0 \le m \le n \label{eq12.5.2} \]
y pendientes seleccionados como
\[S_m = \sin \theta_{m + 1} - \sin \theta_m \ \ \ 0 \le m < n \label{eq12.5.3} \]
\[S_m = 0 \ \ \ m = n \label{eq12.5.4} \]
put distorsión resultante de ubicaciones imprecisas de puntos de interrupción y valores de pendiente es comparable a la distorsión asociada con la aproximación lineal por tramos a menos que se utilicen componentes caros para establecer estos parámetros. Además, está disponible una matriz económica de cinco diodos de circuito integrado. Esta matriz de diodos emparejados se puede utilizar para los cuatro puntos de ruptura, con el quinto diodo proporcionando compensación de temperatura como se describe en el material a seguir. Ecuaciones\(\ref{eq12.5.2}\),\(\ref{eq12.5.3}\) y\(\ref{eq12.5.4}\) evaluadas para\(n = 4\) sugerir puntos de ruptura ubicados en valores variables de entrada de\(20^{\circ}\)\(40^{\circ}\),\(60^{\circ}\), y\(80^{\circ}\), con pendientes de segmento relativas (normalizadas a una pendiente mínima distinta de cero de uno) de 2.879, 2.532, 1.879, 1 y 0, respectivamente.
Con las características de transferencia de la red de conformación determinadas, es necesario diseñar el circuito que sintetice la función requerida. En la discusión de la Sección 11.5.3 se mencionó el uso de conexiones de superdiodos para mejorar la nitidez de los puntos de ruptura en comparación con lo que se puede lograr solo con diodos. Esta técnica no se utilizó para el conformador sinusoidal, ya que el redondeo asociado con las características de avance del diodo normal mejora realmente la calidad del ajuste a la curva sinusoidal.
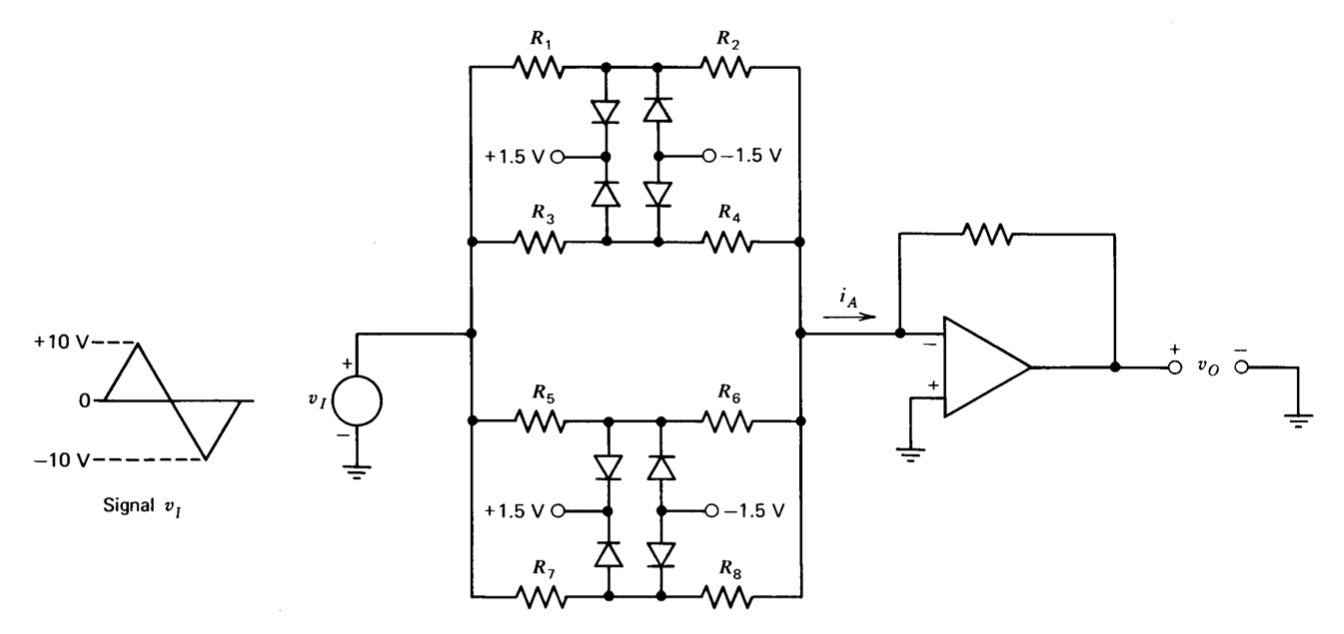
Las no linealidades de tipo compresivo descritas en la Sección 11.5.3 se realizaron utilizando diodos para aumentar la retroalimentación alrededor de un amplificador operacional, reduciendo así su ganancia incremental de bucle cerrado cuando se superó un nivel de punto de interrupción. Una alternativa es usar diodos para disminuir la señal de accionamiento aplicada al amplificador para disminuir la ganancia incremental. Este enfoque simplifica la compensación de temperatura. La topología utilizada se muestra en la Figura 12.34.
El nivel de señal de entrada de pico a pico de 20 voltios corresponde al rango variable de entrada que\(\pm 90^{\circ}\) se muestra en la Figura 12.33. Por lo tanto, las ubicaciones de punto de interrupción de\(\pm 20^{\circ}\)\(\pm 40^{\circ}\)\(\pm 60^{\circ}\),, y\(\pm 80^{\circ}\) corresponden a niveles de voltaje de entrada de\(\pm 2.22\)\(\pm 4.44\) voltios,\(\pm 6.67\) voltios, voltios y\(\pm 8.89\) voltios, respectivamente. Los valores de resistencia se determinan de la siguiente manera. Inicialmente se asume que los diodos son ideales, ya que tienen un voltaje umbral de cero voltios, resistencia cero en la dirección hacia adelante y conductancia cero en la dirección inversa. Supongamos que el\(R_1-R_2\) camino es proporcionar los puntos de ruptura a voltajes de entrada de\(\pm 8.89\) voltios. Dado que la entrada inversora del amplificador operacional está a potencial de tierra, la relación de resistencia necesaria para hacer que el voltaje en el punto medio de estas dos resistencias sea\(\pm 1.5\) voltios con\(\pm 8.89\) voltios en la entrada es
\[\dfrac{R_2}{R_1 + R_2} = \dfrac{1.5}{8.89} = 0.1687 \label{eq12.5.5} \]
Las relaciones de pares de resistencias\(R_3-R_4\)\(R_5-R_6\),, y\(R_7-R_8\) se eligen de manera similar para ubicar los puntos de ruptura restantes.
Las conductancias relativas de las trayectorias resistivas entre la fuente de señal de onda triangular y la entrada inversora del amplificador operacional están restringidas por las pendientes relativas de las características de transferencia deseadas de la siguiente manera. La ganancia incremental de bucle cerrado de la conexión es proporcional a la conductancia de transferencia incremental desde la fuente de señal a la corriente\(i_A\) definida en la Figura 12.34. Con la relación de las dos resistencias en cada trayectoria elegida de acuerdo con relaciones como Ecuación\(\ref{eq12.5.5}\), la conductancia incre de transferencia mental es cero (para diodos ideales) cuando la magnitud de la señal de entrada supera los 8.89 voltios, aumenta a\(1/(R_1 + R_2)\) para magnitudes de señal de entrada entre 6.67 y 8.89 voltios,, aumenta aún más\([1/(R_1 + R_2)] + [1/(R_3 + R_4)]\) para magnitudes de señal de entrada entre 4.44 y 6.67 voltios, etc. si definimos\(1/(R_1 + R_2) = G\), realizar la pendiente relativa correcta para magnitudes de señal de entrada entre 4.44 y 6.67 voltios requiere
\[\dfrac{1}{R_1 + R_2} + \dfrac{1}{R_3 + R_4} = 1.879 G \label{eq12.5.6} \]
La satisfacción de Ecuación\(\ref{eq12.5.6}\) hace que la pendiente en esta señal de entrada alcance 1.879 veces más grande que la pendiente para las señales de entrada entre 6.67 y 8.89 voltios. Las relaciones correspondientes acoplan otros valores de pares de resistencias al\(R_1-R_2\) par.
Los conjuntos de ecuaciones que hacen paralelo a Ecuaciones\(\ref{eq12.5.5}\) y\(\ref{eq12.5.6}\), junto con la selección de cualquier valor de resistencia, determinan\(R_1\) a través de los reistores\(R_8\). El nivel de resistencia general establecido al elegir el valor de resistencia libre se selecciona en función de consideraciones de carga y para asegurar que la capacitancia parásita no deteriore el rendimiento dinámico.
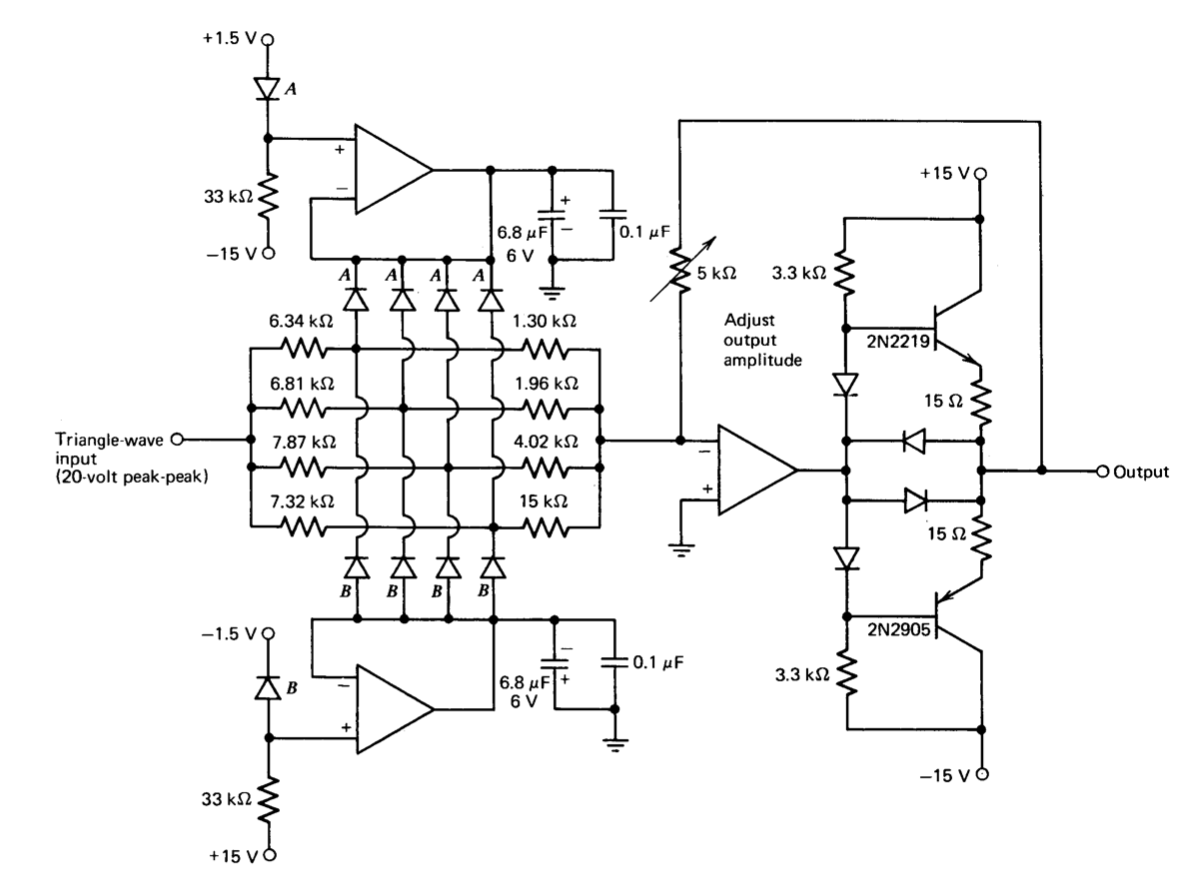
El circuito utilizado para el conformador sinusoidal (Figura 12.35) utiliza los valores estándar de resistencia de 1% de tolerancia que mejor se aproximan a los valores calculados. Los cinco diodos etiquetados\(A\) y los etiquetados\(B\) son de dos matrices de diodos de circuito integrado CA3039. Un miembro de cada matriz modifica los voltajes de polarización para tener en cuenta los voltajes de umbral de diodo y para proporcionar compensación de temperatura. Los diodos compensadores funcionan a un nivel de corriente de aproximadamente la mitad del nivel máximo de corriente de funcionamiento de los diodos de conformación. Si bien este tipo de compensación claramente no tiene ningún efecto sobre las características de conductancia de los diodos de conformación, las características exponenciales del diodo realmente mejoran el rendimiento del circuito como se describió anteriormente.
Dado que este circuito está destinado a operar a 1 MHz (se usa un amplificador operacional de circuito integrado de alta velocidad con un búfer de componentes discretos para aumentar la capacidad de corriente de salida), los condensadores son necesarios en la salida de los amplificadores de voltaje de referencia para disminuir su impedancia de salida en la conmutación frecuencia de los diodos. Los\(1.5-V\) niveles se derivan de los voltajes que establecen la amplitud de onda triangular para que cualquier cambio en esta amplitud provoque los cambios correspondientes en la ubicación del punto de interrupción.
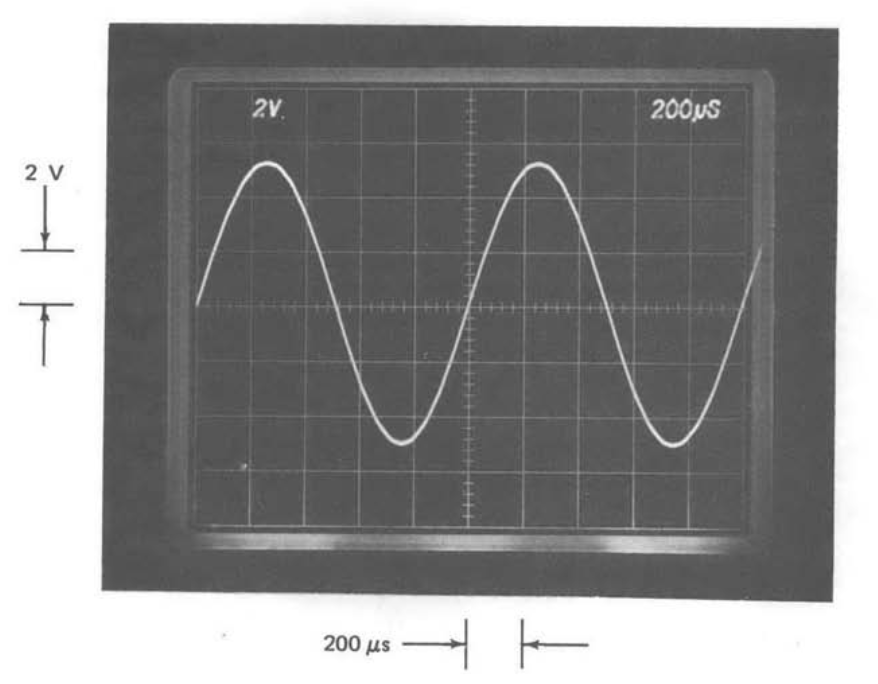
El circuito produce ondas sinusoidales aproximadas con la amplitud de cualquier armónico individual en la señal de salida al menos 40 dB (una relación de voltaje de 100:1) por debajo de la fundamental. Este rendimiento se obtiene sin recorte. Si se realizan ajustes para anular el desplazamiento del amplificador operacional, y se utilizan ajustes empíricos (guiados por un analizador de espectro) para contrarrestar errores de valor de componente y para compensar la resistencia directa de diodo finito, la amplitud de los armónicos de señal de salida individuales se puede reducir a 55 dB por debajo lo fundamental a bajas frecuencias. El rendimiento se deteriora un poco a frecuencias por encima de aproximadamente 10 kHz debido a la ganancia de bucle abierto del amplificador de señal reducida. Una señal de salida de 1 kHz del circuito se muestra en la Figura 12.36.
Red no lineal de tres puertos
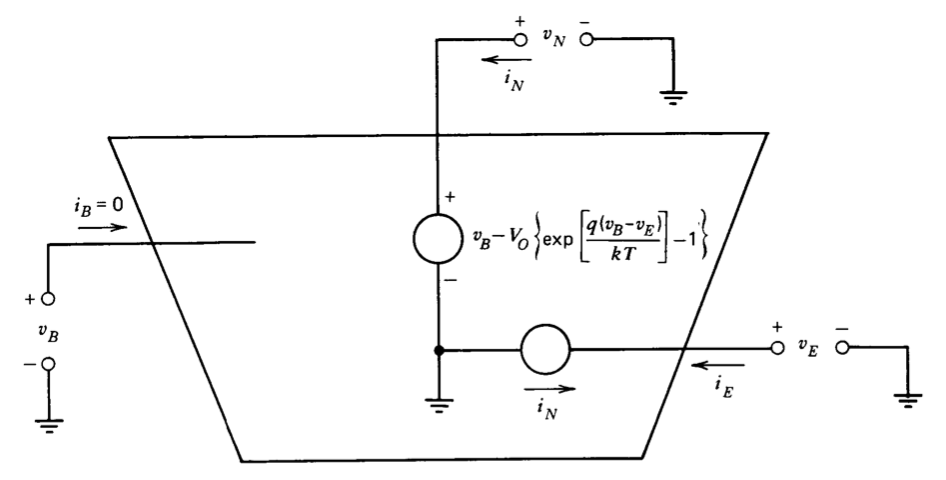
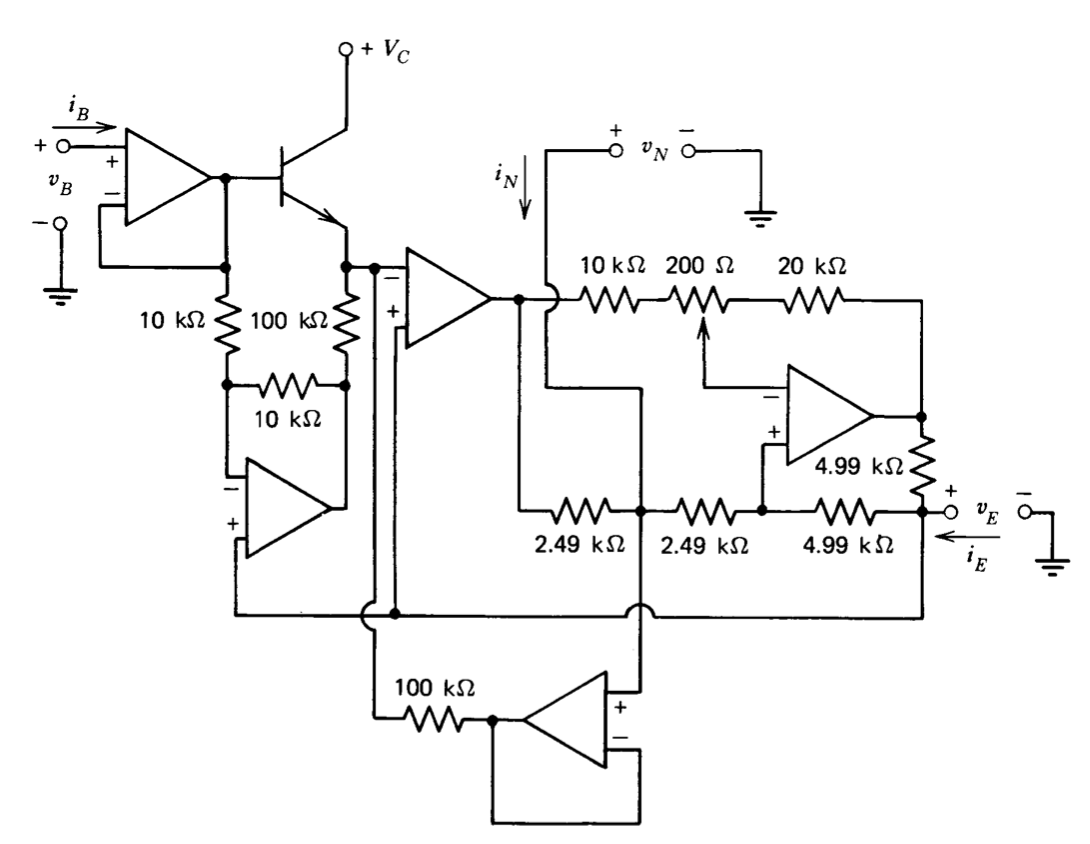
La realización de un dispositivo analógico que puede ser de valor en la enseñanza del comportamiento dinámico de los transistores bipolares requiere una red de tres puertos definida por la Figura 12.37. La síntesis de esta red se inicia diseñando primero un circuito que proporcione la relación
\[v_N = v_B - V_0 \left \{\exp \left [\dfrac{q(v_B - v_E)}{kT} \right ] - 1 \right \}\label{eq12.5.7} \]
El parámetro\(V_O\), como cabría esperar, está relacionado con la cantidad\(I_S\) para el transistor que se está simulando, y en consecuencia es deseable una dependencia de temperatura correspondiente.
Hay una serie de formas de simular la ecuación\(\ref{eq12.5.7}\). Una topología que es adaptable a otros requerimientos se muestra en la Figura 12.38. Dado que una eventual restricción es que la corriente en la\(v_B\) entrada sea cero, se usa un amplificador de búfer en este terminal. El segundo amplificador está conectado diferencialmente con una tensión de salida.
\[v_A = 2v_E - v_B\label{eq12.5.8} \]
El tercer amplificador también está conectado como amplificador diferencial, de manera que
\[v_N = v_E - (i_T + i_A) R \label{eq12.5.9} \]
Dado que la retroalimentación mantiene el terminal de entrada inversora del tercer amplificador a potencial\(v_E\),
\[i_A = \dfrac{v_A -v_E}{R} = \dfrac{v_E - v_B}{R} \label{eq12.5.10} \]
Si asumimos las características habituales del transistor,
\[i_T \simeq I_S \left \{ \exp \left [\dfrac{q(v_B - v_E)}{kT} \right ] - 1 \right \}\label{eq12.5.11} \]
Sustituyendo Ecuaciones\(\ref{eq12.5.10}\) y\(\ref{eq12.5.11}\) en Ecuación\(\ref{eq12.5.9}\) arroja la forma requerida por la Ecuación\(\ref{eq12.5.8}\):
\[v_N = v_B - RI_S \left \{ \exp \left [\dfrac{q(v_B - v_E)}{kT} \right ] - 1 \right \} \nonumber \]
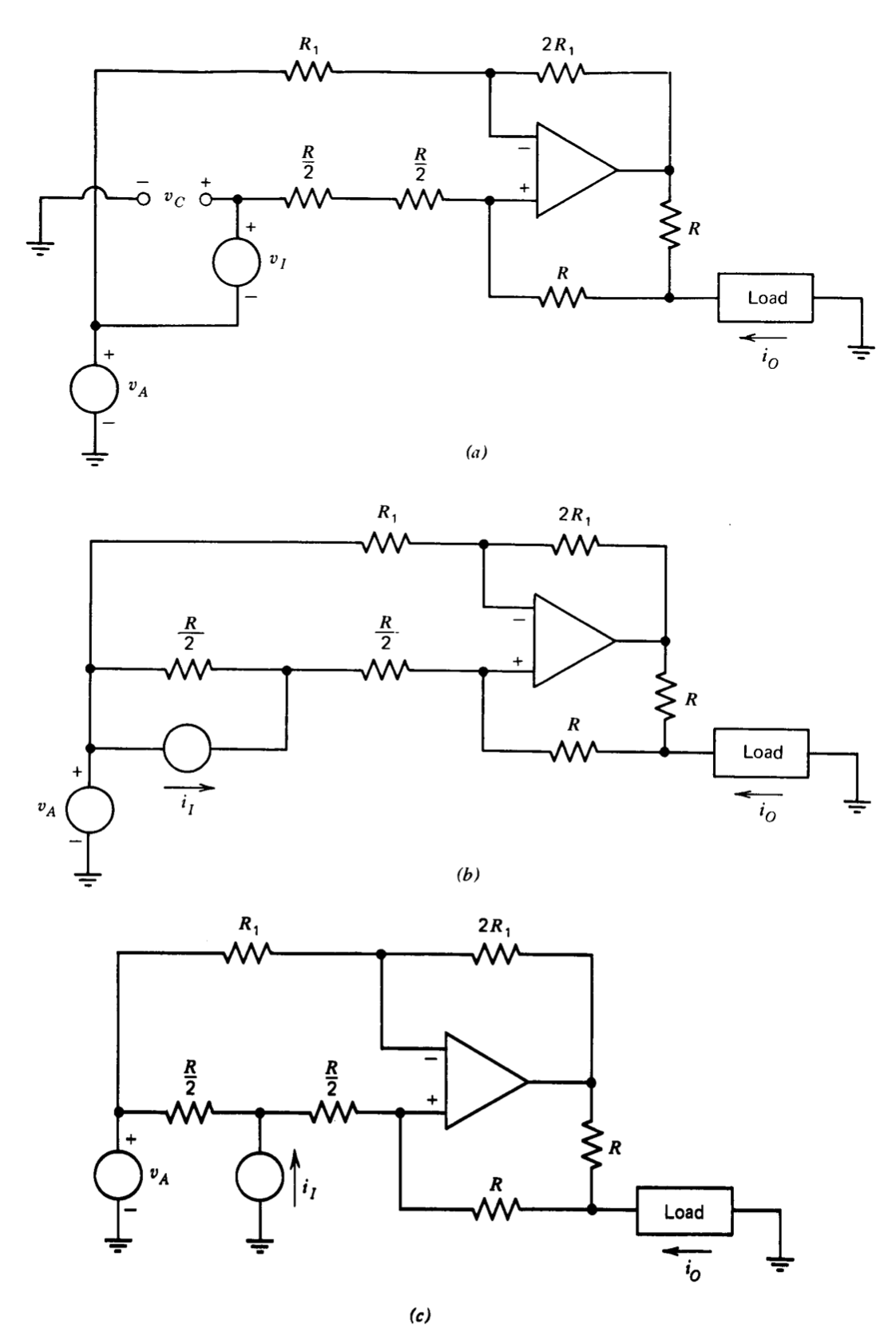
Para completar la síntesis, es necesario muestrear la corriente que fluye en el terminal\(N\) y hacer que la corriente que fluye en\(E\) el terminal sea negativa de esta corriente. Se puede utilizar una modificación de la fuente de corriente Howland (ver Sección 11.4.3). El circuito básico con entradas diferenciales se muestra en la Figura 12.39\(a\). (La razón de la aparentemente extraña conexión de voltaje de entrada y la resistencia dividida se hará evidente momentáneamente). La corriente\(i_O\) para estos valores de parámetro es
\[i_O = \dfrac{2(v_A - v_C)}{R} = \dfrac{2(v_A - v_A - v_I}{R} = \dfrac{-2v_I}{R}\label{eq12.5.13} \]
En la Figura 12.39\(b\), la fuente de voltaje\(v_I\) y la mitad de la resistencia dividida se reemplazan por un circuito equivalente a Norton. Para la equivalencia, es necesario hacer\(i_I = 2v_I/R\). Expresando Ecuación\(\ref{eq12.5.13}\) en términos de\(i_I\) espectáculos
\[i_O = -i_I \nonumber \]
La topología de la Figura 12.39\(b\) muestra que la fuente de\(i_T\) corriente se puede devolver a tierra en lugar de a la fuente de voltaje\(v_A\). Esta modificación se muestra en la Figura 12.39\(c\), la fuente de corriente controlada por corriente necesaria en nuestra presente solicitud. Tenga en cuenta que la salida es independiente de\(v_A\), el voltaje de entrada de modo común aplicado a la fuente de corriente.
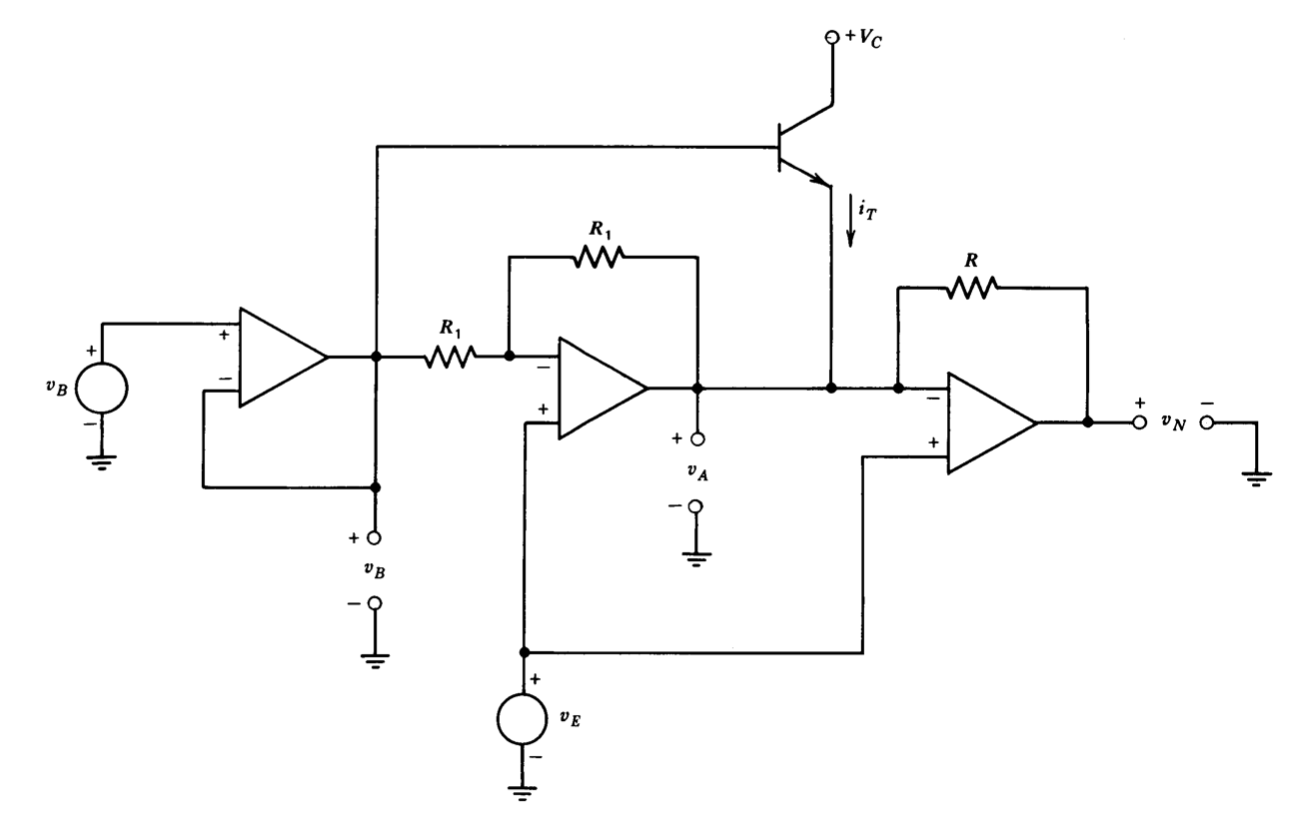
Los circuitos de las figuras 12.38 y 12.39\(c\) se combinan para formar la red de tres puertos como se muestra en la figura 12.40. En este circuito, la retroalimentación para el voltaje\(v_N\) se toma desde el lado de salida de la resistencia de muestreo de corriente para que las caídas de voltaje en esta resistencia no influyan\(v_N\). Es necesario amortiguar la resistencia de\(100-k\Omega\) retroalimentación con un seguidor de ganancia unitaria para asegurar que la corriente a través de esta resistencia no fluya a través de la resistencia de muestreo de corriente y, por lo tanto, se altere\(i_E\).
El potenciómetro de ajuste permite una coincidencia precisa de las relaciones de resistencia para hacer que la corriente sea\(i_E\) independiente de los niveles de voltaje de modo común en varios puntos de la fuente de corriente y, por lo tanto, dependa\(i_N\) En esta aplicación, no fue necesario tener exactamente ganancia de unidad entre\(i_N\) y\(- i_E\), por lo que no se incluye ningún recorte para esta relación. La magnitud general de las resistencias en la fuente de corriente se elige por compatibilidad con los niveles de corriente requeridos y las características del amplificador y no es importante para los fines de esta discusión.
Ejercicio\(\PageIndex{1}\)
Considere un oscilador Wien-Bridge como se muestra en la Figura 12.1. Mostrar que si la señal de salida es de la forma general\(v_O = E \sin [(t/RC) + \theta]\) donde\(\theta\) es una constante, las señales aplicadas a las dos entradas del amplificador operacional son prácticamente idénticas, condición necesaria para un desempeño satisfactorio. Obsérvese que si se intercambian las entradas inversora y no inversora y se supone que la salida tiene la forma indicada anteriormente, las señales en las dos entradas también serán idénticas. Sin embargo, esta topología modificada no funcionará como oscilador. Explique.
Ejercicio\(\PageIndex{2}\)
Se construye un oscilador Wien-Bridge utilizando la topología básica mostrada en la Figura 12.1. Debido a las tolerancias de los componentes, las constantes de tiempo de los brazos en serie y paralelos de la red de retroalimentación dependiente de la frecuencia difieren en 5%. ¿Cómo deben relacionarse los valores de los componentes en la ruta de retroalimentación independiente de la frecuencia para garantizar la oscilación?
Ejercicio\(\PageIndex{3}\)
Utilice un enfoque de función de descripción para analizar el circuito mostrado en la Figura 12.3, asumiendo que el amplificador operacional es ideal y que los diodos tienen conductancia cero hasta que se alcanza una tensión directa de 0.6 voltios y resistencia cero en el estado de conducción directa. En particular, determinar la magnitud de la señal aplicada a la entrada no inversora del amplificador y la distorsión del tercer armónico presente en la salida del amplificador.
Ejercicio\(\PageIndex{4}\)
Un oscilador sinusoidal se construye conectando la salida de un integrador doble (ver Figura 11.12) a su entrada. Mostrar que la amplitud puede ser controlada variando la magnitud de la resistencia con valor (\(R/2\)) mostrada en esta figura. Diseñe un circuito completo que pueda producir una señal de salida\(20-V\) pico a pico a 1 kHz. Utilice un FET con los parámetros dados en la Sección 12.1.4 para el elemento de control. Analice su bucle de control de amplitud para demostrar que tiene una estabilidad aceptable y una frecuencia de cruce compatible con la frecuencia de oscilación de 1 kHz. Si tienes confianza en tu diseño, construirlo. El transistor de efecto de campo 2N4416 está razonablemente bien caracterizado por los parámetros mencionados anteriormente.
Ejercicio\(\PageIndex{5}\)
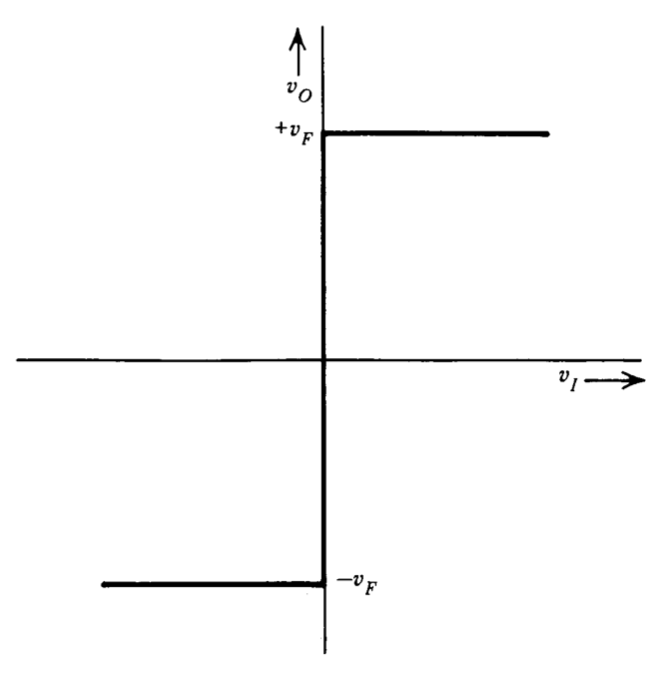
Las discusiones de las Secciones 12.2.2 y 12.2.3 sugieren operar interruptores electrónicos conectados a voltajes variables simétricos a partir de la salida de un disparador Schmitt para dos aplicaciones diferentes. Una alternativa al uso de interruptores es utilizar un circuito que tenga la característica de transferencia mostrada en la Figura 12.41 para la función de conformación necesaria. (En este diagrama, el voltaje\(v_F\) es una variable positiva). Diseñar un circuito que utilice amplificadores operacionales para sintetizar esta característica de transferencia. Sus niveles de salida deben ser insensibles a las variaciones de temperatura.
Ejercicio\(\PageIndex{6}\)
Un sistema de suspensión magnética fue descrito en la Sección 6.2.3. Desarrollar una simulación electrónica analógica de este sistema que permita determinar los transitorios que resultan de las fuerzas perturbadoras aplicadas al balón. Supongamos que, además de los amplificadores operativos y los componentes pasivos apropiados, están disponibles multiplicadores con un factor de escala\(v_O = v_Xv_Y/10\) voltios. Una forma de realizar la división requerida en esta simulación utilizando un multiplicador y un amplificador operacional se describe en la Sección 6.2.2.
Puede dejar los distintos valores de elementos en la simulación definidos en términos de parámetros del sistema, sin desarrollar valores finales escalados en amplitud.
Ejercicio\(\PageIndex{7}\)
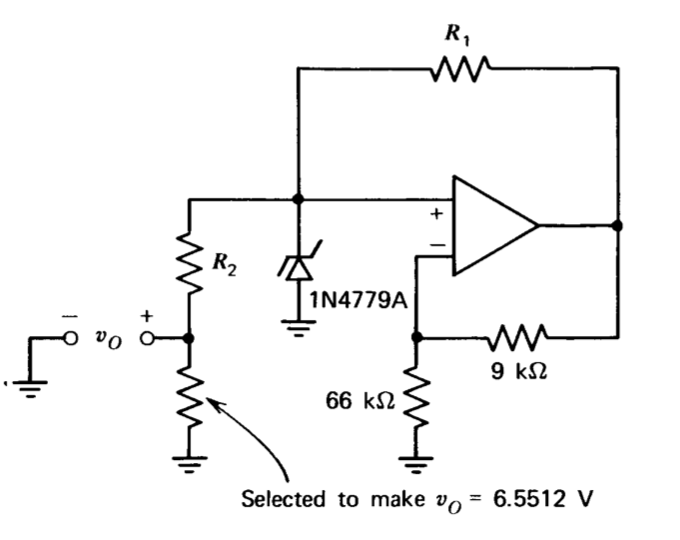
En la Figura 12.42 se muestra un circuito destinado a ser utilizado como referencia de voltaje de precisión para un convertidor analógico-digital. El circuito utiliza una fracción del voltaje del diodo Zener como salida. Si bien este método que implica atenuación resistiva da como resultado una resistencia de salida relativamente alta en comparación con el uso de la tensión en la salida del amplificador como referencia, la tensión de salida se vuelve esencialmente independiente de la tensión de compensación del amplificador operativo.
El voltaje de ruptura especificado del 1N4779A es de 8.5 voltios\(\pm 5\)%. La resistencia indicada se selecciona durante la prueba para obtener el voltaje de salida requerido independientemente del valor real del voltaje del diodo Zener.
El rango de voltaje de ruptura y el coeficiente de temperatura del dispositivo están garantizados a una corriente de funcionamiento de\(0.500\ mA\). Mediante la elección adecuada de\(R_1\) y\(R_2\), es posible hacer que la corriente a través del diodo Zener sea independiente de la tensión Zener real después de que se haya completado la selección única indicada. Tal elección es ventajosa ya que simplifica la calibración del circuito en oposición a los métodos que requieren dos o más ajustes interdependientes para establecer la tensión de salida y la corriente de funcionamiento del diodo Zener. Encuentra valores para\(R_1\) y\(R_2\) que resulten en esta simplificación. (Por favor, disculpe los números algo difíciles de manejar involucrados en este problema, pero se extrae directamente de una aplicación existente).
Ejercicio\(\PageIndex{8}\)
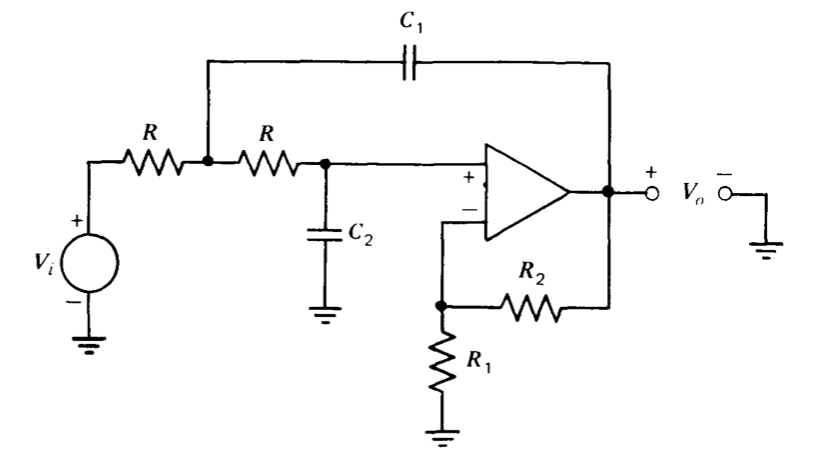
En la Figura 12.43 se muestra un circuito de paso bajo Sallen y Key con una ganancia de voltaje de bucle cerrado del amplificador mayor que la unidad. Determine la función de transferencia\(V_o(s)/V_i(s)\) para este circuito. Compara la sensibilidad de este circuito a las variaciones de componentes con la de la versión unidad-ganancia.
Ejercicio\(\PageIndex{9}\)
Una forma de analizar el circuito Sallen y Key que se muestra en la Figura 12.43 es reconocer la configuración como un circuito de retroalimentación positiva. Si el bucle se rompe en la entrada no inversora al amplificador operacional, se pueden utilizar técnicas de análisis basadas en las propiedades de transmisión de bucle.
(a) Indicar el patrón de singularidad de transmisión de bucle que resulta cuando el bucle se rompe en el punto antes mencionado. No es necesario determinar ubicaciones de singularidad exactamente en términos de valores de elementos.
(b) Mostrar cómo los polos de bucle cerrado del sistema se mueven en función de la ganancia de bucle cerrado del amplificador operacional mediante el uso de métodos de locus raíz que han sido modificados adecuadamente para sistemas de retroalimentación positiva.
Ejercicio\(\PageIndex{10}\)
Diseñe un filtro Butterworth de sexto orden con una frecuencia de esquina de 1 kHz mediante la conexión en cascada de tres circuitos Sallen y Key de ganancia unitaria.
Ejercicio\(\PageIndex{11}\)
El Pad6 de quinto orden aproximado a un retraso de tiempo de un segundo es
\[P_5 (s) = \dfrac{1 - 0.5s + 0.111s^2 - 1.39 \times 10^{-2} s^3 + 9.92 \times 10^{-4} s^4 - 3.31 \times 10^{-5} s^5}{1 + 0.5s + 0.111s^2 - 1.39 \times 10^{-2} s^3 + 9.92 \times 10^{-4} s^4 + 3.31 \times 10^{-5} s^5}\nonumber \]
Diseñar un filtro activo que sintetice esta función de transferencia.
Ejercicio\(\PageIndex{12}\)
Desarrollar un diagrama de bloques linealizado para el sistema mostrado en la Figura 12.32, asumiendo que el FET se caracteriza por los parámetros dados en la Sección 12.1.4. Demuestre que la frecuencia de cruce de bucle es baja en comparación con 400 Hz para cualquier nivel de voltaje de entrada de hasta 20 voltios pico a pico. Estimar el tiempo requerido para que el sistema restablezca el equilibrio después de una perturbación incremental (iniciada, por ejemplo, por un cambio en la frecuencia de entrada) cuando la amplitud de la señal de entrada es de 100 mV pico a pico. Obsérvese que el sistema no se ve perturbado significativamente por un cambio en la amplitud de entrada cuando opera en condiciones de equilibrio, y que por lo tanto este tiempo de asentamiento relativamente largo no deteriora el rendimiento.