12.4: FILTROS ACTIVOS
- Page ID
- 84126
Existen numerosas aplicaciones que requieren la realización de una función de transferencia particular. Una de las muchas limitaciones del diseño de redes de filtros que utilizan solo componentes pasivos es que se requieren inductores para obtener ubicaciones complejas de polos. Esta restricción se elimina si se incluyen elementos activos en los diseños, y los filtros activos resultantes permiten la realización de polos complejos usando solo resistencias y condensadores además de los elementos activos. Otras ventajas de la síntesis de filtro activo incluyen la posibilidad de una amplia gama de impedancias relativas de entrada y salida, y el uso de componentes reactivos más pequeños y menos costosos de lo que normalmente es posible con diseños pasivos.
Hay una buena cantidad de investigaciones actuales dedicadas a mejorar las técnicas para la síntesis de filtros activos, y la probabilidad es que evolucionen mejores diseños, particularmente con respecto a la sensibilidad (la dependencia de la función de transferencia de las variaciones en los valores de los parámetros). Esta sección describe dos topologías actualmente populares que se pueden utilizar para realizar filtros activos.
Sallen y circuito de llave
R. P. Sallen y E. L. Key, “Un método práctico de diseño de filtros activos RC”, Instituto de Ingenieros de Radio, Transacciones sobre Teoría de Circuitos, marzo de 1955, pp. 74-85.
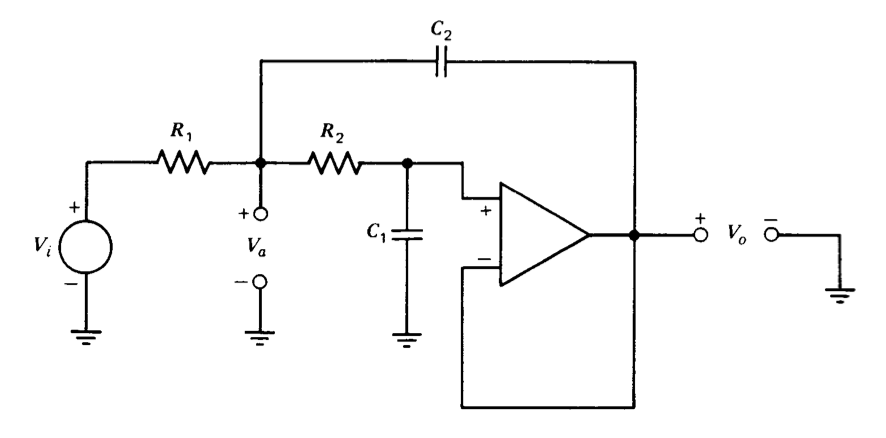
Figura 12.22 Filtro activo de paso bajo de segundo orden.
La Figura 12.22 muestra un circuito de filtro activo que utiliza un amplificador operacional conectado con ganancia de unidad. Las ecuaciones de nodo para el circuito se escriben fácilmente al señalar que el voltaje en la entrada no inversora del amplificador es igual al voltaje de salida y son
\[\begin{array} {rcl} {G_1 V_i} & = & {(G_1 + G_2 + C_2s)V_a - (G_2 + C_2s)V_o} \\ {0} & = & {-G_2 V_a + (G_2 + C_1 s)V_o} \end{array} \nonumber \]
Resolviendo los rendimientos de la función de transferencia
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{1}{R_1 R_2 C_1 C_2 s^2 + (R_1 + R_2) C_1 s + 1} \nonumber \]
Esta ecuación representa una función de transferencia de segundo orden con parámetros de forma estándar
\[\omega_n = \dfrac{1}{\sqrt{R_1 R_2 C_1 C_2}} \nonumber \]
y
\[\zeta = \dfrac{R_1 + R_2}{2 \sqrt{R_1R_2}} \sqrt{\dfrac{C_1}{C_2}} \nonumber \]
Dado que solo se requieren dos cantidades para caracterizar el filtro de segundo orden, los cuatro grados de libertad representados por los cuatro valores de componentes pasivos son redundantes. Parte de esta redundancia se elimina frecuentemente al elegir\(R_1 = R_2 = R\). En este caso, los parámetros de forma estándar se convierten en
\[\omega_n = \dfrac{1}{R\sqrt{C_1 C_2}} \nonumber \]
y
\[\zeta = \sqrt{\dfrac{C_1}{C_2}} \nonumber \]
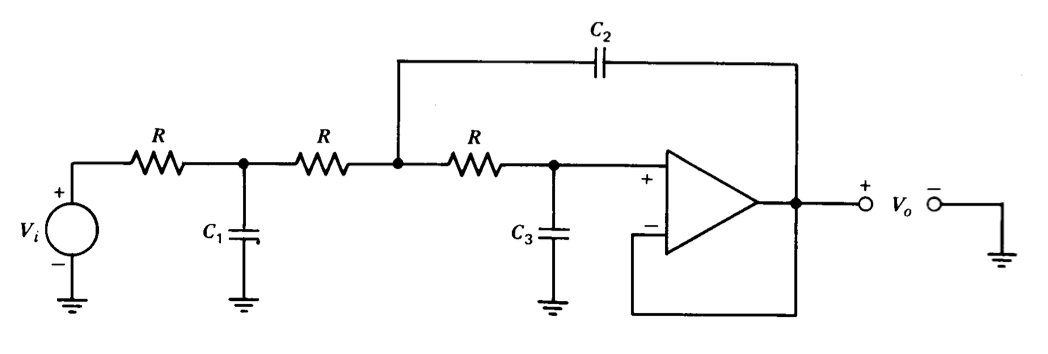
Figura 12.23 Filtro activo de paso bajo de tercer orden.
La adición de otra sección al filtro activo de paso bajo de segundo orden como se muestra en la Figura 12.23 permite la síntesis de una función de transferencia de tercer orden con un solo amplificador. Si se utilizan resistencias de igual valor como se muestra, la función de transferencia es
\[\dfrac{V_o(s)}{V_i (s)} = \dfrac{1}{C_1 C_2 C_3 R^3 s^3 + 2(C_1 C_3 + C_2 C_3) R^2 s^2 + (C_1 + 3C_3) Rs + 1} \nonumber \]
Un filtro de paso bajo de\(n\) orden th a menudo se diseña combinando secciones de\(n/2\) segundo orden en el caso de n pares, o una sección de tercer orden con secciones de\(n/2 - 3/2\) segundo orden cuando\(n\) es impar. Mesas (Farouk Al-Nasser, “Tablas Speed Design of Low-Pass Active Filters”, EDN, 15 de marzo de 1971, pp. 23-32.) que simplifican la selección del valor del elemento están disponibles para filtros de hasta el décimo orden con varios patrones de polos diferentes.
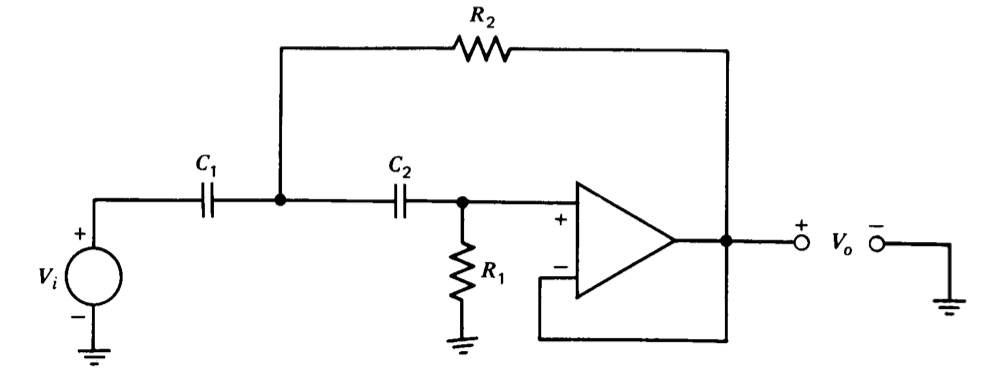
El cambio de resistencias y capacitores como se muestra en la Figura 12.24 cambia el filtro de paso bajo de segundo orden a un filtro de paso alto. La función de transferencia para esta configuración es
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{R_1 R_2 C_1 C_2 s^2}{R_1 R_2 C_1 C_2 s^2 + R_2 (C_1 + C_2) s + 1}\label{eq12.4.8} \]
Si, en un desarrollo análogo al utilizado para el filtro de paso bajo, elegimos\(C_1 = C_2 = C\), Ecuación\(\ref{eq12.4.8}\) reduce a
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{s^2/\omega_n^2}{(s^2/\omega_n^2) + (2\zeta s/\omega_n) + 1} \nonumber \]
donde
\[\omega_n = \dfrac{1}{C\sqrt{R_1 R_2}}\nonumber \]
y
\[\zeta = \sqrt{\dfrac{R_2}{R_1}}\nonumber \]
El circuito Sallen y Key se puede diseñar con una ganancia de amplificador que no sea la unidad (ver Problema P12.8). Esta modificación permite una mayor flexibilidad, ya que la ganancia de baja o alta frecuencia del circuito se puede hacer distinta a una. Sin embargo, la relación de amortiguación de las funciones de transferencia realizadas de esta manera depende de los valores de las resistencias que establecen la ganancia del amplificador de bucle cerrado; por lo tanto, los polos pueden estar ubicados de manera algo menos confiable. Otra ventaja de la versión unidad-ganancia es que puede construirse utilizando el circuito integrado LM 110 (ver Sección 10.4.4). El ancho de banda de este amplificador supera con creces el de la mayoría de las unidades de circuito integrado de propósito general, y las frecuencias de esquina en el rango de megahercios bajos se pueden obtener usando él.
Procedimiento General de Síntesis
La configuración de Sallen y Key, junto con muchas otras topologías de filtro activo, permite una completa libertad en la elección de la ubicación de los polos, pero no permite la colocación arbitraria de ceros de función de transferencia. La aplicación de los conceptos de cómputos analógicos descritos en la Sección 12.3.1 permite la síntesis de cualquier función de transferencia realizable que sea expresable como una relación de polinomios en s, siempre que el número de polos sea igual o mayor que el número de ceros en la función de transferencia.
Considere la función de transferencia
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{b_n s^n + b_{n - 1} s^{n - 1} + \cdots + b_1 s + b_0}{a_n s^n + a_{n - 1} s^{n - 1} + \cdots + a_1 s + a_0}\label{eq12.4.10} \]
El primer paso es introducir una variable intermedia\(V_a (s)\) tal que\(V_a(s)/ V_i(s)\) contenga solo los polos de la función de transferencia, o
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{1}{a_n s^n + a_{n - 1} s^{n - 1} + \cdots + a_1 s + a_0} \nonumber \]
Procediendo de una manera exactamente paralela al desarrollo en el dominio del tiempo de la Sección 12.3.1, escribimos
\[s^n V_a (s) = -\dfrac{a_{n - 1}}{a_n} s^{n -1} V_a (s) - \cdots - \dfrac{a_1}{a_n} s V_a (s) - \dfrac{a_0}{a_n} V_a (s) + \dfrac{V_i (s)}{a_n} \label{eq12.4.12} \]
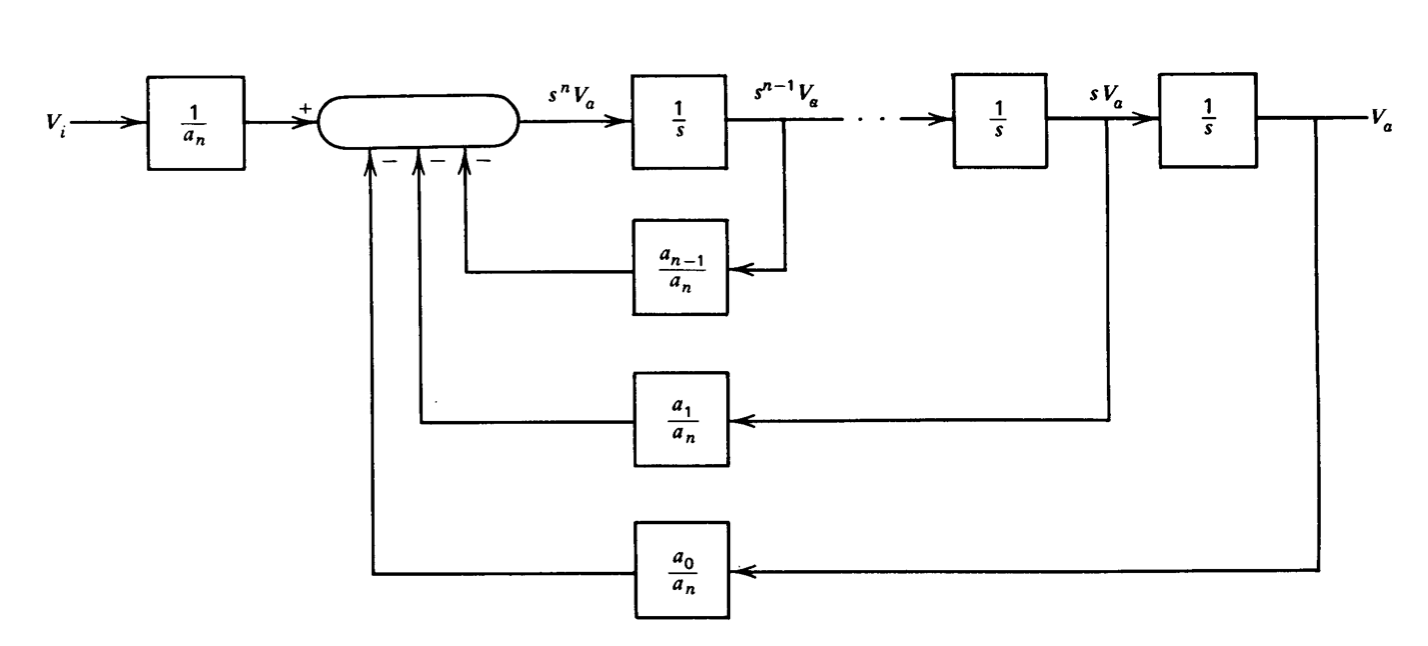
La representación de diagrama de bloques de la Ecuación\(\ref{eq12.4.12}\) se muestra en la Figura 12.25. Este diagrama de bloques se puede implementar fácilmente usando veranos e inte grators. Para completar la síntesis de nuestra función de transferencia (Ecuación\(\ref{eq12.4.10}\)) reconocemos que
\[V_o (s) = V_a (s) (b_n s^n + b_{n - 1} s^{n - 1} + \cdots + b_1 s + b_0)\label{eq12.4.13} \]
La característica esencial de la Ecuación\(\ref{eq12.4.13}\) es que indica\(V_o(s)\) es una combinación lineal de\(V_a(s)\) y sus primeras\(n\) derivadas. Dado que todas las variables necesarias aparecen en el diagrama de bloques, se\(V_o (s)\) pueden generar simplemente escalando y sumando estas variables, sin necesidad de diferenciación.
Este procedimiento de síntesis se ilustra para una aproximación a un retardo de tiempo puro conocido como el aproximado de Pade. El retardo de tiempo tiene una función de transferencia\(e^{-s \tau}\), donde\(\tau\) está la duración del retardo. La magnitud de esta función de transferencia es una en todas las frecuencias, mientras que su desplazamiento de fase negativo es linealmente proporcional a la frecuencia. El retardo de tiempo tiene una singularidad esencial en el origen, y por lo tanto no se puede representar exactamente como una relación de polinomios en\(s\).
La expansión de la serie de Taylor de\(e^{-s \tau}\) es
\[e^{-s\tau} = 1 - s \tau + \dfrac{s^2 \tau^2}{2!} - \cdots + \cdots + (-1)^m \dfrac{s^m \tau^m}{m!} + \cdots \nonumber \]
El Pade se aproxima a ubicar un número igual de polos y ceros para acordar con el máximo número posible de términos de la expansión de la serie Taylor's. Esta aproximación siempre conduce a una red de paso completo que tiene ceros de medio plano derecho y polos de medio plano izquierdo ubicados simétricamente con respecto al eje imaginario. Este tipo de patrón de singularidad da como resultado una magnitud independiente de la frecuencia para la función de transferencia.
Dado que siempre podemos escalar la frecuencia o el tiempo en un momento posterior, consideramos un retraso de tiempo unitario\(e^{-s}\) para simplificar el desarrollo. El Padede de primer orden aproximado a esta función es
\[P_1 (s) = \dfrac{1 - (s/2)}{1 + (s/2)} = 1 - s + \dfrac{s^2}{2} - \dfrac{s^3}{4} + \cdots - \cdots + \nonumber \]
La expansión para\(e^{-s}\) es
\[e^{-s} = 1 - s + \dfrac{s^2}{2} - \dfrac{s^3}{6} + \dfrac{s^4}{24} - \dfrac{s^5}{120} + \dfrac{s^6}{720} - \cdots + \nonumber \]
La aproximación de primer orden coincide con los dos primeros coeficientes\(s\) de la expansión completa, y está en concordancia razonable con el tercer coeficiente. Este partido es todo lo que se puede esperar, ya que sólo se dispone de dos grados de libertad (la ubicación del polo y la ubicación del cero) para la aproximación de primer orden. El Plade de segundo orden aproximado a un retraso de tiempo de un segundo es
\[P_2 (s) = \dfrac{1 - (s/2) + (s^2/12)}{1 + (s/2) + (s^2/12)} = 1 - s + \dfrac{s^2}{2} - \dfrac{s^2}{2} - \dfrac{s^3}{6} + \dfrac{s^4}{24} - \dfrac{s^5}{144} + \cdots - \cdots +\label{eq12.4.17} \]
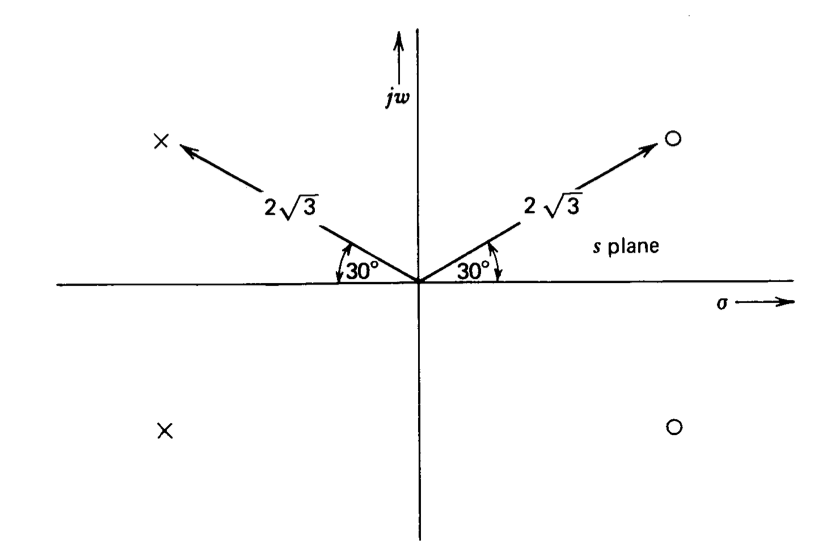
Figura 12.26 Ubicaciones de singularidad para Pade de segundo orden aproximadas a un retraso de tiempo de un segundo.
Como era de esperar, los primeros cuatro coeficientes de retardo de tiempo de\(s\) son emparejados por la aproximación. La gráfica\(s\) -plano para\(P_2(s)\) se muestra en la Figura 12.26. Las manipulaciones simples de vectores confirman el hecho de que la magnitud de esta función es una en todas las frecuencias.
El desplazamiento de fase de la función de aproximación es (de la ecuación\(\ref{eq12.4.17}\))
\[\measuredangle P_2 (j \omega) = 2\measuredangle \left [1 - \dfrac{j \omega}{2} + \dfrac{(j \omega)^2}{12} \right ] = -2 \tan^{-1} \left \{\dfrac{\omega}{2[1 - (\omega^2/12)]} \right \} \nonumber \]
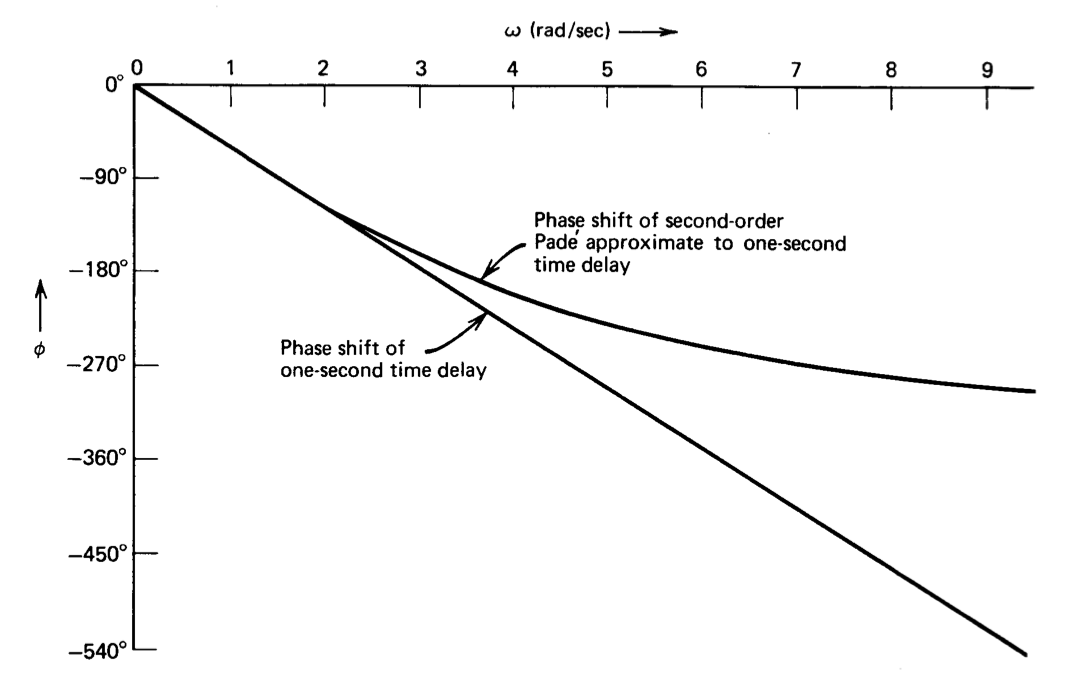
Esta función se compara con un ángulo de\(-57.3^{\circ} \omega\) (el valor para un retardo de tiempo de un segundo) en la Figura 12.27. Observamos una excelente concordancia con frecuencias de aproximadamente 2 radianes por segundo, lo que implica que la aproximación representa bien la función real para la excitación sinusoidal a esta frecuencia, con creciente discrepancia a frecuencias más altas. El error refleja el hecho de que el desplazamiento de fase negativo máximo del Pade aproximado es\(360^{\circ}\), mientras que el retardo de tiempo proporciona un desplazamiento de fase negativo ilimitado a una frecuencia suficientemente alta.
La síntesis se inicia definiendo una variable intermedia\(V_a (s)\) de acuerdo con las Ecuaciones\(\ref{eq12.4.11}\) y\(\ref{eq12.4.12}\), o
\[\dfrac{V_a(s)}{V_i (s)} = \dfrac{1}{(s^2/12) + (s/2) + 1} \nonumber \]
y
\[s^2 V_a (s) = -6s V_o (s) - 12V_a (s) + 12 V_i (s) \nonumber \]
El voltaje de salida es
\[V_o (s) = \dfrac{s^2}{12} V_a (s) - \dfrac{s}{2} V_a (s) + V_a (s) \nonumber \]
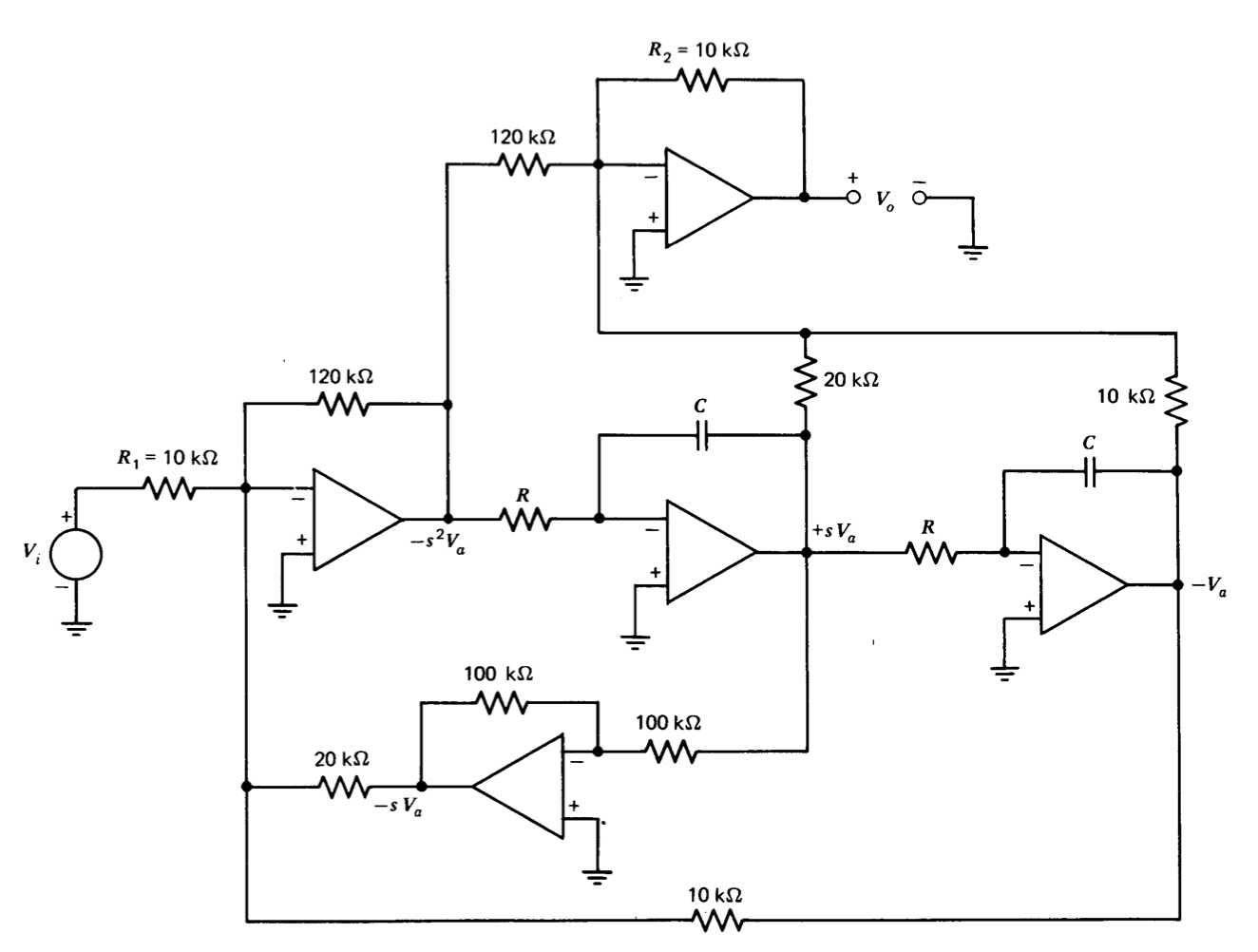
Figura 12.28 Síntesis de Pade de segundo orden aproximada a un retardo de tiempo.
La síntesis operacional-amplificador que se muestra en la Figura 12.28 proporciona la función de transferencia requerida en\(RC = 1\) segundo lugar. El lector debe convencerse a sí mismo de que las libertades tomadas con inversiones y diversos valores de resistencia sí conducen de hecho a la relación deseada.
Las amplitudes anticipadas dependen del nivel de señal de entrada y su contenido espectral. Por ejemplo, si se aplica un paso a la entrada del circuito, la magnitud de la señal del primer amplificador debe ser inicialmente 12 veces mayor que la amplitud de paso, ya que las salidas de los integradores no pueden cambiar instantáneamente para restar del nivel de señal de entrada. Tenga en cuenta, sin embargo, que la función de transferencia de entrada a salida del circuito sigue siendo la misma para cualquier valor de\(R_1 = R_2\). Si, por ejemplo, se esperan cambios de paso de 10 V en la entrada, la selección de\(R_1 = R_2 = 120\ k\Omega\) limitará el nivel de señal en la salida del primer amplificador a 10 voltios mientras se mantiene la ganancia correcta de entrada a salida.
El circuito mostrado en la Figura 12.28 se construyó utilizando\(R = 100\ k\Omega\) y\(C = 0.01\ \mu F\), valores que dieron como resultado una aproximación a un retardo de tiempo de 1 ms. Esta elección de escala de tiempo es conveniente para la presentación de osciloscopio. Las señales de entrada y salida para excitación de onda sinusoidal de 100 Hz se muestran en la Figura 12.29\(a\). El tiempo de retardo entre estas dos señales es de 1 ms dentro de las tolerancias de instrumentación. Este rendimiento refleja la predicción de la Figura 12.27, ya que se anticipa un buen acuerdo a 2000 rad/seg o 300 Hz para la aproximación a un retardo de 1 ms.
Las señales de entrada y salida para excitación de onda triangular de 100 Hz se muestran en la Figura 12.29\(b\). La onda triangular contiene solo armónicos impares, y estos armónicos caen como el cuadrado de su frecuencia. Así, la amplitud del tercer armónico de la onda triangular es aproximadamente del 11% de la amplitud de la fundamental, la amplitud del quinto armónico es 4% de la fundamental, mientras que los armónicos superiores se atestiguan aún más. Notamos que el circuito funciona muy bien al aproximar un retardo de tiempo de 1 ms la mayor parte del tiempo. La aberración que resulta inmediatamente después de un cambio en la pendiente refleja la incapacidad del circuito para proporcionar un desplazamiento de fase adecuado a los componentes de mayor frecuencia.
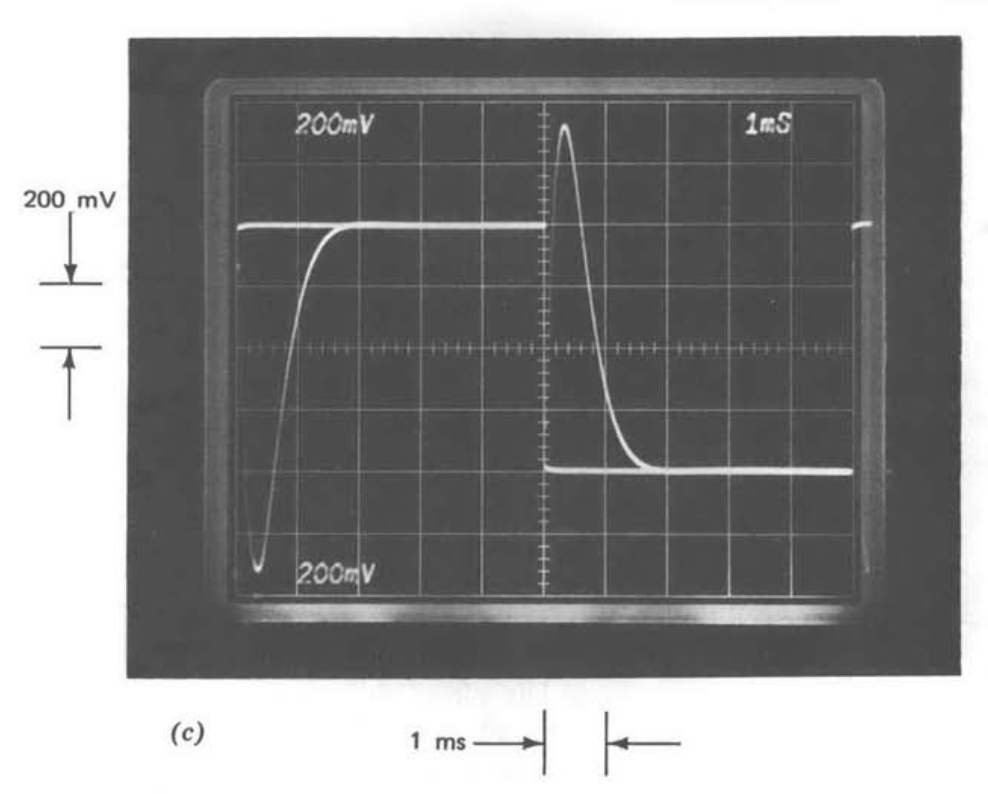
El rendimiento del circuito cuando se excita con una onda cuadrada de 100 Hz se muestra en la Figura 12.29\(c\). El comportamiento relativamente peor en las proximidades de una transición en este caso resulta del mayor contenido armónico de la onda cuadrada. (Recordemos que la onda cuadrada contiene armónicos impares que caen solo como la primera potencia de la frecuencia.)


