2.2: Un modelo atómico

Para entender el comportamiento del circuito eléctrico debemos definir primero qué es lo que estamos persiguiendo. En última instancia, los circuitos eléctricos tienen que ver con el movimiento de la carga eléctrica. ¿A qué nos referimos con cargo? Para responder a esa pregunta, necesitamos llegar a un modelo utilizable de un átomo, es decir, una descripción funcional de su estructura interna. Sin duda, los átomos son mucho más pequeños de lo que la mayoría de la gente imagina Hay muchos más átomos en un galón de agua que galones de agua en todos los océanos, lagos y ríos del planeta Tierra combinados. No tendría sentido preguntar cómo podría “verse” un átomo porque sus componentes son todos más pequeños que las longitudes de onda de luz más cortas que los humanos pueden ver. Eso sería un poco como preguntarle a un humano cómo suena un silbato de perro, cuando de hecho está en un tono que es más alto de lo que los humanos pueden escuchar. Sin embargo, en última instancia, todo lo que realmente necesitamos es un modelo que explique su comportamiento observado.

Quizás el modelo más prolífico en la imaginación popular es el modelo planetario que se muestra en la Figura 2.2.1 , así llamado porque recuerda a modelos simples de nuestro sistema solar. En este modelo, el núcleo, o núcleo, se dibuja en el centro y contiene protones cargados positivamente y neutrones no cargados. Girando alrededor de este núcleo hay electrones cargados negativamente, cada uno siguiendo un camino agradable, regular y plano muy parecido a un planeta alrededor del sol. Desafortunadamente, este modelo no es exacto por decir lo menos, aunque su popularidad a veces puede llevar a conclusiones tremendamente erróneas y oscuramente humorísticas. A pesar de su inexactitud, los componentes (núcleo, protones, neutrones y electrones) son perfectamente válidos. Antes de llegar a un modelo más preciso y útil, echemos un vistazo más de cerca a estos artículos.

Figura 2.2.1 : Modelo atómico planetario: Popular pero tristemente incorrecto. Fuente de la imagen (modificada)

A diferencia de las personas, todas las partículas de un tipo son indistinguibles: cada protón es idéntico a cada otro protón y cada electrón es idéntico a cada otro electrón. El número de protones determina cuál es el elemento. El elemento más simple, el hidrógeno, tiene un solo protón en su núcleo. En contraste, el helio tiene dos protones en su núcleo y el cobre tiene 29. El núcleo también puede contener un número de neutrones (no necesariamente igual al número de protones). En cualquier átomo estable, el número de electrones será igual al número de protones. Si no son lo mismo, al átomo se le llama ion (técnicamente, un catión tiene menos electrones que protones y un anión es su opuesto). Con una fuente de energía externa, es posible separar un electrón de un átomo. Esto nos deja con un electrón y un átomo que ahora tiene una carga neta positiva. Es esta capacidad de separar estas partículas, y así separar la carga, lo que da origen a nuestro concepto de electricidad incluyendo elementos tales como corriente y voltaje, como veremos.

La mayor parte de la masa de un átomo dado proviene de los protones y neutrones. Los protones y neutrones tienen masas similares, aproximadamente 1.67E−24 gramos cada uno. La masa de un electrón es aproximadamente 2000 veces menor. El radio de un protón es de aproximadamente 0.87E−15 metros y la distancia media al electrón más cercano es de aproximadamente 5.3E−11 metros. Por lo tanto, un electrón está aproximadamente 60,000 veces más alejado del protón que el tamaño de dicho protón. Para poner esto en perspectiva, eso es aproximadamente lo mismo que la relación entre una pelota de golf y una esfera con un radio de 3/4 de milla o 1200 metros. Este sería el caso de un átomo de hidrógeno ya que consiste en un solo protón y electrón. La magnitud de esta relación no es muy diferente para otras sustancias, incluyendo cosas como el diamante y el cuarzo que son muy duras y sólidas. Si piensas en eso por un momento, te das cuenta de que la idea de “solidez” es en cierto modo una ilusión porque la gran mayoría de lo que llamamos “algo” es realmente solo espacio vacío (como una pelota de golf traqueteando dentro de una esfera que tiene una milla y media de ancho). En realidad, la sensación de solidez cuando agarras algo con la mano es solo el resultado de la interacción de las fuerzas atómicas entre tu mano y el objeto. En efecto, si de alguna manera pudiéramos deshacernos de ese “espacio vacío”, podríamos colocar una montaña dentro de un automóvil (aunque probablemente requeriría una suspensión severamente mejorada).

Para nuestro trabajo inmediato, quizás el tema más importante es el de la carga, parte esencial de la teoría del electromagnetismo. Se mencionó que los protones están cargados positivamente y los electrones están cargados negativamente. Entonces, ¿qué es el cargo? La carga no es un atributo físico obvio como la altura o el color de ojos de alguien. Se acerca más a una característica conductual. Decir que una partícula está cargada es como decir que alguien tiene una personalidad atractiva. La magnitud de la carga en un electrón es la misma que la magnitud de la carga sobre un protón. La única diferencia es la polaridad: los protones están cargados positivamente mientras que los electrones están cargados negativamente. Algo importante para recordar es que las partículas con la misma polaridad se repelen entre sí mientras que los opuestos se atraen a ¹.

La carga se mide en culombios, que llevan el nombre de Charles-Augustin de Coulomb, un físico francés del siglo XVIII. La carga en un solo electrón es minúscula, apenas 1.602E−19 culombios. Como alternativa, se necesitan 6.242E18 electrones para crear una carga de un culombo. Más sobre esto en un momento.

Uno de los principales problemas con el modelo planetario es la idea de que los electrones giran alrededor del núcleo en órbitas estables similares a planetas. Eso simplemente no es cierto. En primer lugar, el electrón habita en una región del espacio 3D y no se mueve simplemente a través de un plano. Segundo, debido al Principio de Incertidumbre de Heisenberg, no podemos trazar con precisión la posición y trayectoria de un electrón dado. Lo mejor que podemos hacer es hacer una gráfica de dónde es probable que esté el electrón. A esto se le llama contorno de probabilidad. Para entender este concepto, imagina que podrías registrar la posición de un electrón específico en relación con el núcleo en un momento específico. Un momento después se registra su nueva posición, un momento después de eso se graba la siguiente posición, y así sucesivamente para miles de mediciones. Si intentabas trazarlos todos, terminarías con una nube de puntos alrededor del núcleo. A esta nube se le conoce como orbital. No sabrías cómo llegaba el electrón de una posición a otra pero te darías una idea general de dónde era probable que estuviera. En última instancia, una órbita no se parece en nada a una órbita planetaria.

Una buena analogía con un contorno de probabilidad de electrones es el mapeo del vuelo de las aves migratorias. Por ejemplo, cierto grupo de gansos de Canadá podría migrar de su rango de verano en el extremo norte de Canadá a su morada de verano en el sur de Estados Unidos a través de la sección s de Atlantic Flyway, tal vez a través del centro del estado de Nueva York, como se muestra en púrpura, en la Figura 2.2.2 . El camino aéreo te dice dónde es probable que se encuentren estas aves mientras migran. Si están tomando la ruta por el centro de Nueva York, en algún momento es probable que algún ganso en particular de esa bandada se encuentre cerca de las ciudades de Utica, Siracusa y así sucesivamente. Es mucho menos probable que algún ganso en particular de ese rebaño se encuentre en Ohio o New Hampshire. Texas, por supuesto, está justo fuera. El flyway da una buena cantidad de datos sobre dónde es probable que estén estas aves pero de ninguna manera puede predecir con precisión dónde estará un ave individual en una fecha específica, ni precisamente dónde terminará su migración.

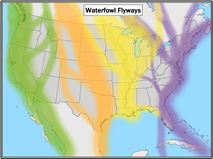
Figura 2.2.2 : Comportamiento electrónico versus aves migratorias.

Al regresar de nuestro desvío aviar, observamos que existen varios orbitales potenciales. Debido a la física cuántica, sólo se permiten ciertos orbitales. Los niveles permisibles de energía electrónica se agrupan primero en conchas, luego subconchas y finalmente orbitales. Es importante recordar que los orbitales indican el nivel de energía electrónica. Es decir, un orbital superior implica un mayor nivel de energía. Además, los orbitales se llenan primero desde el nivel de energía más bajo hasta el nivel de energía más alto.

Las conchas se denotan por su número cuántico principal,\(n\); 1, 2, 3, etc. Cuanto mayor sea el número, más subconchas puede contener. Las subconchas se designan por letras, siendo los primeros cuatro\(s\),\(p\),\(d\), y\(f\). Shell 1 contiene solo subshell\(s\) mientras que shell 2 contiene tipos de subshell\(s\) y\(p\). Shell 3 contiene tipos de subshell\(p\) y\(s\)\(d\), y así sucesivamente. Estas subconchas también pueden tener variaciones dentro de ellas. Hay una variación sobre\(s\), tres variaciones sobre\(p\), cinco variaciones sobre\(d\), etc. Estas variaciones son los orbitales y cada orbital puede contener un máximo de dos electrones.

Al juntar todo esto, encontramos que el primer caparazón puede contener un máximo de dos electrones: dos en la única\(s\) subcapa orbital (\(1s\)). El segundo caparazón puede contener un máximo de ocho electrones: dos en la\(s\) subcapa (\(2s\)) más dos en cada uno de los tres orbitales de\(p\) subcapa (\(2p\)). De igual manera, el tercer caparazón puede contener un máximo de 18 electrones: dos en\(3s\), seis en\(3p\) y dos en cada uno de los orbitales de las cinco\(d\) subconchas (\(3d\)). Puedes condensar esto en una fórmula simple:

\[\text{Number of electrons per shell } = 2n^2, \text{ where } n \text{ is the shell number} \nonumber \]

La figura 2.2.3 muestra el contorno de probabilidad de electrones del orbital más interno, es decir,\(1s\) (es decir, el número cuántico principal 1, subshell\(s\)). Como se puede ver, es de forma esférica. El núcleo se encuentra en el centro, oscurecido aquí. Todos los\(s\) orbitales tienen una forma esférica similar aunque las partes internas cambian. \(1s\)es la órbita de menor energía.

Figura 2.2.3 : Contorno de probabilidad de electrones para orbitales más internos, 1s.

Los orbitales no se limitan a formas esféricas simples. Los orbitales de orden superior pueden tomar una variedad de formas. La figura 2.2.4 muestra un contorno de probabilidad de electrones mucho más complejo. El núcleo está situado en el centro de los anillos concéntricos. Obviamente, esto no se parece en nada a las órbitas elípticas de buen comportamiento de los planetas alrededor del sol (ni los caminos de las aves migratorias, a menos que estén muy confundidas).

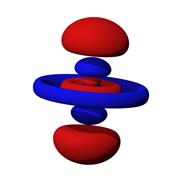
Figura 2.2.4 : Un contorno de probabilidad de electrones de orden superior.

Tan visualmente interesantes como son estos gráficos, son engorrosos de trabajar con ellos. En consecuencia, se requiere un gráfico más funcional. Tal dispositivo es el modelo Bohr, que lleva el nombre del físico danés Niels Bohr. Un ejemplo se muestra en la Figura 2.2.5 .

Figura 2.2.5 : Modelo genérico de Bohr.

Es importante entender que el modelo de Bohr es una descripción energética del átomo, no un intento de imitar su apariencia física o estructura. El núcleo se coloca en el centro. Está rodeado por anillos concéntricos que representan las conchas de electrones. Cuanto mayor sea el número, mayor será el anillo y mayor será el nivel de energía. Si un electrón pasara de un nivel superior a un nivel inferior, la diferencia de energía se irradia hacia fuera. Esto podría ser en forma de calor o luz. Este es un punto que vale la pena recordar. Por ejemplo, esta transición es lo que hace que los diodos emisores de luz (LEDs) funcionen. También es posible lo inverso, es decir, que al absorber energía, un electrón puede moverse hacia un orbital superior. Este es un concepto igualmente poderoso.

Usando el modelo Bohr podemos crear diagramas para representar elementos individuales. Por ejemplo, el cobre tiene un número atómico de 29 lo que significa que tiene 29 protones y 29 electrones. La configuración de la capa de electrones es 2-8-18-1. Es decir, los tres primeros proyectiles están completamente llenos y hay un solo electrón en el cuarto caparazón. El modelo Bohr para cobre simplemente mostraría cuatro anillos, los tres primeros siendo llenados y con un solo electrón en el cuarto anillo. Esto se muestra en la Figura 2.2.6 . En esta versión, los electrones individuales se dibujan en cada caparazón y el número atómico se indica en el núcleo. Nuevamente, por favor no imaginen esto representando electrones individuales orbitando el núcleo en carriles. Esta es una representación del nivel de energía.

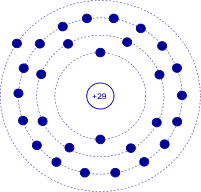
Figura 2.2.6 : Modelo Bohr de cobre.

Vale la pena señalar que un electrón exterior solitario solo está ligado flojamente al núcleo, lo que hace que el movimiento de carga a través de dicho material sea relativamente fácil, dada la aplicación de alguna fuente de energía externa. En consecuencia, el cobre es un muy buen conductor. Esta es una característica compartida por los metales comunes: son buenos conductores porque solo tienen uno o dos electrones holgados en su capa exterior. Los ejemplos incluyen plata, oro y aluminio (un electrón externo para cada uno, siendo todos muy buenos conductores); y hierro, estaño y níquel (dos electrones externos para cada uno, y este grupo no es tan conductor como los del primer grupo).

Referencias

¹ La pregunta obvia podría ser “¿Por qué no se rompe el núcleo?” La respuesta es que la fuerza nuclear fuerte subatómica tiene un mayor efecto a distancias atómicas que el electromagnetismo, y así une los protones y neutrones juntos en el núcleo.