Saltar al contenido principal
LibreTexts Español

5.6: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    86015

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Análisis

    1. En el circuito de la Figura 5.6.1 , ¿qué resistencias individuales están estrictamente en serie y cuáles están en paralelo?

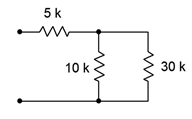
    clipboard_e7b0286d69f61fcf3d33cc4260b801ad2.png

    Figura 5.6.1

    2. En el circuito de la Figura 5.6.2 , ¿qué resistencias individuales están estrictamente en serie y cuáles están en paralelo?

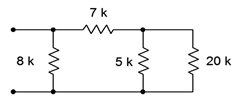
    clipboard_e7b4ba4997381757b6dece288d5bf503f.png

    Figura 5.6.2

    3. En el circuito de la Figura 5.6.3 , ¿qué resistencias individuales están estrictamente en serie y cuáles están en paralelo?

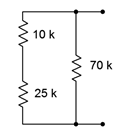
    clipboard_e3989c6919f01d4638a71931253533fbe.png

    Figura 5.6.3

    4. En el circuito de la Figura 5.6.4 , ¿qué resistencias individuales están estrictamente en serie y cuáles están en paralelo?

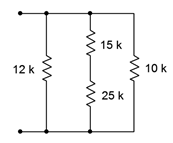
    clipboard_ef37f0127892e4711a396dbf50ff04f9c.png

    Figura 5.6.4

    5. En el circuito de la Figura 5.6.5 , ¿qué resistencias individuales están estrictamente en serie y cuáles están en paralelo?

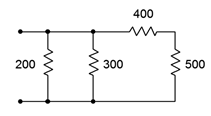
    clipboard_ee09ef628d93ac132794d516b24e6c433.png

    Figura 5.6.5

    6. En el circuito de la Figura 5.6.6 , ¿qué resistencias individuales están estrictamente en serie y cuáles están en paralelo?

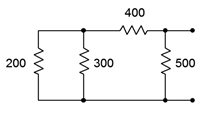
    clipboard_e81973856ddffddd35f0e356f63e4734a.png

    Figura 5.6.6

    7. En el circuito de la Figura 5.6.7 , ¿qué resistencias individuales están estrictamente en serie y cuáles están en paralelo?

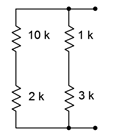
    clipboard_ec31d21d1e2fdc4db081aaa21c7f4ad60.png

    Figura 5.6.7

    8. En el circuito de la Figura 5.6.8 , ¿qué resistencias individuales están estrictamente en serie y cuáles están en paralelo?

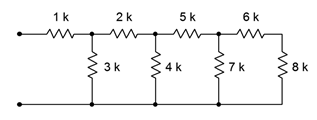
    clipboard_ef949f6121398622338d314837006b220.png

    Figura 5.6.8

    9. Determinar la resistencia equivalente de la red mostrada en la Figura 5.6.1 (es decir, como si un ohmiómetro estuviera conectado a los dos terminales).

    10. Determinar la resistencia equivalente de la red mostrada en la Figura 5.6.2 .

    11. Determinar la resistencia equivalente de la red mostrada en la Figura 5.6.3 .

    12. Determinar la resistencia equivalente de la red mostrada en la Figura 5.6.4 .

    13. Determinar la resistencia equivalente de la red mostrada en la Figura 5.6.5 .

    14. Determinar la resistencia equivalente de la red mostrada en la Figura 5.6.6 .

    15. Determinar la resistencia equivalente de la red mostrada en la Figura 5.6.7 .

    16. Determinar la resistencia equivalente de la red mostrada en la Figura 5.6.8 .

    17. Para el circuito de la Figura 5.6.9 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

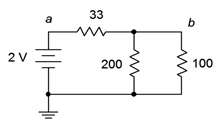
    clipboard_e5b1e4c97a47f4276f3b79484560cd59d.png

    Figura 5.6.9

    18. Para el circuito de la Figura 5.6.9 , encuentra la corriente a través de cada resistor.

    19. Para el circuito de la Figura 5.6.10 , encuentra la corriente a través de cada resistor.

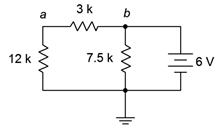
    clipboard_e0998ac87b0220a1ffa292ff17afcd37a.png

    Figura 5.6.10

    20. Para el circuito de la Figura 5.6.10 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

    21. Para el circuito de la Figura 5.6.11 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

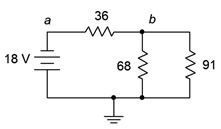
    clipboard_e1f15fc334c5e7b7cf9c160e0a842651c.png

    Figura 5.6.11

    22. Para el circuito de la Figura 5.6.11 , encuentra la corriente a través de cada resistor.

    23. Para el circuito de la Figura 5.6.12 , encuentra la corriente a través de cada resistor.

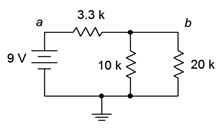
    clipboard_ee83e437cc499a6c688299e2cfbd0a6a5.png

    Figura 5.6.12

    24. Para el circuito de la Figura 5.6.12 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

    25. En el circuito de la Figura 5.6.13 , encontrar voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

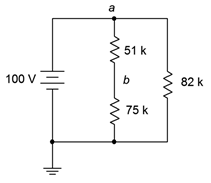
    clipboard_e286758ebe5729017425d15ed93f44450.png

    Figura 5.6.13

    26. En el circuito de la Figura 5.6.13 , encuentra la corriente a través de cada resistor.

    27. En el circuito de la Figura 5.6.14 , encuentra la corriente a través de cada resistor.

    28. En el circuito de la Figura 5.6.14 , encontrar voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

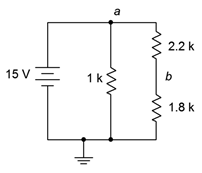
    clipboard_ea391889d50c1541c0e8b08d377077af9.png

    Figura 5.6.14

    29. Para el circuito de la Figura 5.6.15 , busque voltajes\(V_b\),\(V_c\) y\(V_{cb}\).

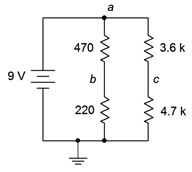
    clipboard_ef235b43275903f9b725c3b0d4e95c3e6.png

    Figura 5.6.15

    30. Para el circuito de la Figura 5.6.15 , encuentra la corriente a través de las\(\Omega\) resistencias 470\(\Omega\) y 3.6 k junto con la corriente fuente.

    31. Para el circuito de la Figura 5.6.16 , encuentra la corriente a través de las\(\Omega\) resistencias de 2 k\(\Omega\) y 5.1 k junto con la corriente de fuente.

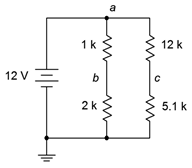
    clipboard_ef6fb015edd281c806b592a24ed1a5ffa.png

    Figura 5.6.16

    32. Para el circuito de la Figura 5.6.16 , encontrar voltajes\(V_c\),\(V_b\),\(V_{bc}\) y\(V_{ab}\).

    33. Para el circuito de la Figura 5.6.17 , encuentre voltajes\(V_a\) y\(V_b\).

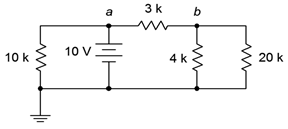
    clipboard_e219f327d951b8e5ed23bdebac0d8713f.png

    Figura 5.6.17

    34. Para el circuito de la Figura 5.6.17 , encuentra la corriente a través de las\(\Omega\) resistencias de 10 k\(\Omega\) y 4 k junto con la corriente de fuente.

    35. Para el circuito de la Figura 5.6.18 , encuentra la corriente a través de las\(\Omega\) resistencias de 30 k\(\Omega\) y las 36 k más a la izquierda junto con la corriente de origen.

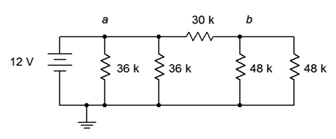
    clipboard_eb9b3423b5816690065a17af42447b3e7.png

    Figura 5.6.18

    36. Para el circuito de la Figura 5.6.18 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

    37. En el circuito de la Figura 5.6.18 , ¿deben ser las mismas las corrientes a través de las dos\(\Omega\) resistencias de 36 k? ¿Por qué no?

    38. En el circuito de la Figura 5.6.18 , ¿deben ser las mismas las corrientes a través de las dos\(\Omega\) resistencias de 48 k? Además, estas corrientes deben ser las mismas que las corrientes a través de las dos\(\Omega\) resistencias de 36 k ¿por qué?/¿Por qué no?

    39. Para el circuito de la Figura 5.6.19 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

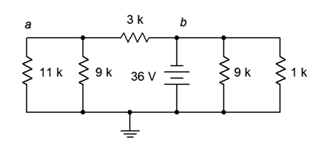
    clipboard_e807f74736acc37d992933344b0c27be0.png

    Figura 5.6.19

    40. Para el circuito de la Figura 5.6.19 , encuentra la corriente a través de las\(\Omega\) resistencias de 3 k\(\Omega\)\(\Omega\), 11 k, y ambas de 9 k.

    41. Dado el circuito de la Figura 5.6.20 , encuentra la corriente a través de las\(\Omega\) resistencias de 47 k\(\Omega\)\(\Omega\), 5.1 k y 3.9 k.

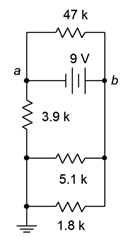
    clipboard_efab5441093a5e877d7f18c0660f7b704.png

    Figura 5.6.20

    42. Dado el circuito de la Figura 5.6.20 , encontrar voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

    43. Para el circuito de la Figura 5.6.21 , busque voltajes\(V_b\),\(V_c\) y\(V_d\).

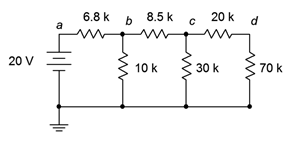
    clipboard_e150f6b9bb2668f77f0a1899b3a83269d.png

    Figura 5.6.21

    44. Para el circuito de la Figura 5.6.21 , encuentra la corriente a través de las\(\Omega\) resistencias 6.8 k\(\Omega\)\(\Omega\), 8.5 k y 20 k.

    45. El circuito de la Figura 5.6.22 se llama escalera R-2R. Encuentra la corriente a través de cada una de las\(\Omega\) resistencias de 60 k.

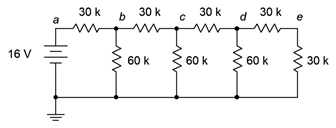
    clipboard_ee1917e7c0f8dd1a36a6f8acf18970ae9.png

    Figura 5.6.22

    46. Dado el circuito de la Figura 5.6.22 , encontrar voltajes\(V_b\),\(V_c\),\(V_d\) y\(V_e\). ¿Qué tiene de único esta configuración?

    47. Para el circuito de la Figura 5.6.23 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

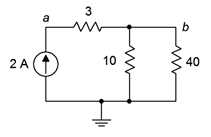
    clipboard_ecc617e0b532d142d10e986e9989fc90c.png

    Figura 5.6.23

    48. Para el circuito de la Figura 5.6.23 , encuentra la corriente a través de cada una de las resistencias.

    49. Para el circuito de la Figura 5.6.24 , encuentra la corriente a través de cada una de las resistencias.

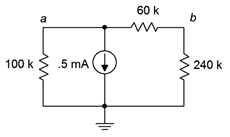
    clipboard_e4747c9f1d237eca644085428baa86f77.png

    Figura 5.6.24

    50. Para el circuito de la Figura 5.6.24 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

    51. Dado el circuito de la Figura 5.6.25 , encontrar voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

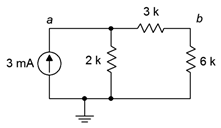
    clipboard_e0ecf6b5a3a86ed52afa77524ae864480.png

    Figura 5.6.25

    52. Dado el circuito de la Figura 5.6.25 , encuentra la corriente a través de cada una de las resistencias.

    53. Para el circuito de la Figura 5.6.26 , encuentra la corriente a través de las\(\Omega\) resistencias 200\(\Omega\)\(\Omega\), 400 y 100.

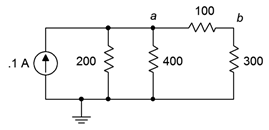
    clipboard_e764669045893e9cbf0ff868b6c9afe3a.png

    Figura 5.6.26

    54. Para el circuito de la Figura 5.6.26 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

    55. Dado el circuito de la Figura 5.6.27 , encontrar voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

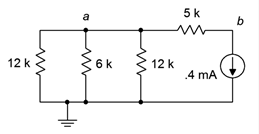
    clipboard_ed2d80550ad56a8ae3287fc0fee10d7ac.png

    Figura 5.6.27

    56. Dado el circuito de la Figura 5.6.27 , encuentra la corriente a través de las\(\Omega\) resistencias de 5 k\(\Omega\), y 6 k.

    57. Para el circuito de la Figura 5.6.28 , encuentra la corriente a través de las\(\Omega\) resistencias de 9 k\(\Omega\) y 82 k más a la derecha.

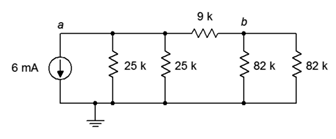
    clipboard_ed1091d55556b5b048be4d782be32e560.png

    Figura 5.6.28

    58. Para el circuito de la Figura 5.6.28 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

    59. ¿La corriente a través de las\(\Omega\) resistencias de 82 k debe ser idéntica en el circuito de 4.8.6? ¿Por qué no?

    60. ¿La corriente a través de las\(\Omega\) resistencias de 25 k debe ser idéntica en el circuito de 4.8.6? ¿Deben ser las mismas que las corrientes a través de las\(\Omega\) resistencias de 82 k? ¿Por qué no?

    61. Para el circuito de la Figura 5.6.29 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

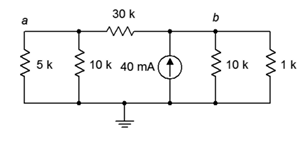
    clipboard_e8ed824652666907c6d9b6e0f61627d2b.png

    Figura 5.6.29

    62. Para el circuito de la Figura 5.6.29 , encuentra la corriente a través de las\(\Omega\) resistencias de 30 k\(\Omega\)\(\Omega\), 5 k y 1 k.

    63. Para el circuito de la Figura 5.6.30 , encuentre la corriente a través de las\(\Omega\) resistencias de 1 k\(\Omega\)\(\Omega\), 2.2 k y 18 k.

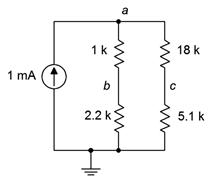
    clipboard_e316348131616834920ce3cfec1f613b5.png

    Figura 5.6.30

    64. Para el circuito de la Figura 5.6.30 , busque voltajes\(V_a\),\(V_b\) y\(V_c\).

    65. Dado el circuito de la Figura 5.6.31 , encontrar voltajes\(V_a\),\(V_b\) y\(V_{ab}\).

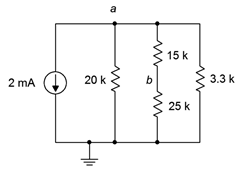
    clipboard_e8b19c2f2946bc7e5a336d81d6b641f76.png

    Figura 5.6.31

    66. Dado el circuito de la Figura 5.6.31 , encuentra la corriente a través de las\(\Omega\) resistencias de 20 k\(\Omega\)\(\Omega\), 15 k y 3.3 k.

    67. El circuito de la Figura 5.6.32 se conoce como una red de escalera R-2R. Encuentra la corriente a través de cada una de las\(\Omega\) resistencias de 4 k.

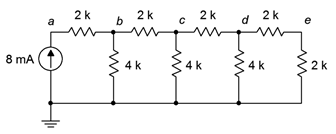
    clipboard_e7368b455ab95ebc744839cbee7e8c87a.png

    Figura 5.6.32

    68. Para el circuito de la Figura 5.6.32 , busque voltajes\(V_a\),\(V_b\) y\(V_{ab}\). ¿Cuál es la característica única de esta configuración?

    Diseño

    69. Determine un nuevo valor para la\(\Omega\) resistencia 33 en la Figura 5.6.9 tal que la corriente de la fuente sea de 10 mA.

    70. Determine un nuevo valor para la\(\Omega\) resistencia de 20 k en la Figura 5.6.12 tal que\(V_b\) sea de 4 voltios.

    71. Determine un nuevo valor para la\(\Omega\) resistencia 470 en la Figura 5.6.15 tal que\(V_b\) sea de 6 voltios.

    72. Determine un nuevo valor para la\(\Omega\) resistencia de 1 k en la Figura 5.6.14 tal que la corriente de la fuente sea de 20 mA.

    73. Determine un nuevo valor para la\(\Omega\) resistencia de 12 k en la Figura 5.6.16 tal que\(V_{bc}\) sea 0 voltios.

    74. Dado el circuito de la Figura 5.6.24 , determinar un nuevo valor para la\(\Omega\) resistencia de 100 k tal que\(V_a\) sea de 75 voltios.

    75. Dado el circuito de la Figura 5.6.23 , determinar un nuevo valor para la fuente de corriente tal que\(V_b\) sea de 8 voltios.

    76. Determine un nuevo valor para la\(\Omega\) resistencia de 2.2 k en la Figura 5.6.30 tal que\(V_{bc}\) sea 0 voltios.

    77. Dado el circuito de la Figura 5.6.32 , determinar un nuevo valor para la fuente de corriente tal que\(V_e\) sea de 1 voltio.

    Desafío

    78. Utilizando solo\(\Omega\) resistencias de 1 k, crea una combinación serie-paralelo que logra 1.25 k\(\Omega\) de resistencia total.

    79. Utilizando solo\(\Omega\) resistencias de 12 k, crea una combinación serie-paralelo que logra 9 k\(\Omega\) de resistencia total.

    80. Considere el circuito de la Figura 5.6.22 . Alterar los valores de las dos\(\Omega\) resistencias de 30 k más a la derecha de tal manera que\(V_e\) sea 1.2 voltios. Los voltajes restantes de los nodos deben permanecer sin cambios respecto al circuito original.

    81. Alterar el circuito que se muestra en la Figura 5.6.22 de tal manera que se agregue otro “escurro” a la escalera creando un nuevo nodo más a la derecha\(f\). Si la primera\(\Omega\) resistencia de 30 k que termina (es decir, la vertical) se restablece a 60 k\(\Omega\), determine los valores de las resistencias en el nuevo escurtido de tal manera que\(V_f\) sea de 0.5 voltios.

    82. Dado el circuito de la Figura 5.6.25 , determinar un nuevo valor para la\(\Omega\) resistencia de 2 k tal que\(V_b\) sea de 12 voltios.

    83. Dado el circuito de la Figura 5.6.32 , determinar nuevos valores para las resistencias de tal manera que todos los voltajes de nodo sean el doble del valor de los voltajes de nodo del circuito original.

    Simulación

    84. Realizar una simulación de CC sobre el resultado del problema 24 para verificar los voltajes de los nodos.

    85. Realizar una simulación de CC sobre el resultado del problema 25 para verificar los voltajes de los nodos.

    86. Realizar una simulación de CC sobre el resultado del problema 43 para verificar los voltajes de los nodos.

    87. Realizar una simulación de CC sobre el resultado del problema 46 para verificar los voltajes de los nodos.

    88. Realizar una simulación de CC sobre el resultado del problema 51 para verificar los voltajes de los nodos.

    89. Realizar una simulación de CC sobre el resultado del problema 68 para verificar los voltajes de los nodos.

    90. Realizar una simulación de CC sobre la solución propuesta al problema 69 para verificar el nuevo diseño.

    91. Realizar una simulación DC de la alteración presentada en Desafío problema 80. ¿El nuevo diseño cumple con todos los requisitos?

    92. Realizar una simulación DC de la alteración solicitada en el problema de desafío 83. ¿El nuevo diseño cumple con todos los requisitos?

    This page titled 5.6: Ejercicios is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by James M. Fiore via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.