1.6: Cálculos de potencia de RF

1.6.1 Propagación de RF

A medida que una señal de RF se propaga lejos de un transmisor, la densidad de potencia reduce la conservación de la potencia en la onda EM. En ausencia de obstáculos y sin atenuación atmosférica la potencia total que pasa por la superficie de una esfera centrada en un transmisor es igual a la potencia transmitida. Dado que el área de la esfera de radio\(r\) es\(4πr^{2}\), la densidad de potencia, por ejemplo\(\text{W/m}^{2}\), en, a una distancia\(r\) cae como\(1/r^{2}\). Con obstáculos, la onda EM puede difractar, reflejar y seguir múltiples caminos hacia un receptor donde puede combinarse destructiva o constructivamente. Es la interferencia destructiva lo que preocupa ya que esto limita la recepción confiable de una señal. Existe una baja probabilidad de que ocurra una cancelación perfecta y, en cambio, se encuentra que la densidad de potencia\(1/r^{n}\) se reduce a medida que\(n\) va desde\(2\) el espacio libre hasta\(5\) para un entorno urbano denso con muchos obstáculos, sin línea de visión y múltiples rutas de señal.

Ejemplo\(\PageIndex{1}\): Signal Propagation

Se recibe una señal a una distancia\(r\) de un transmisor y la energía recibida se desconecta como\(1/r^{2}\). Cuando\(r = 1\text{ km}\),\(100\text{ nW}\) se recibe. ¿Qué es\(r\) cuando es el poder recibido\(100\text{ fW}\)?

Solución

La señal recogida por el receptor es proporcional a la densidad de potencia de la señal EM. La potencia de la señal recibida\(P_{r} = k/r^{2}\) donde\(k\) es una constante. Esto lleva a

\[\label{eq:1}\frac{P_{r}(1\text{ km})}{P_{r}(r)}=\frac{100\text{ nW}}{100\text{ fW}}=10^{6}=\frac{kr^{2}}{k(1\text{ km})^{2}}=\frac{r^{2}}{(10^{3}\text{ m})^{2}};\quad r=\sqrt{10^{12}\text{ m}^{2}}=1000\text{ km} \]

Ejemplo\(\PageIndex{2}\): Signal Propagation With Obstructions

Un transmisor envía una señal a un receptor en un entorno suburbano que está a una\(d\) distancia. Cuando\(d = 5\text{ km}\) la potencia de la señal recibida es\(100\text{ nW}\). A qué distancia del transmisor se encuentra la señal recibida de manera confiable\(1\text{ pW}\) si la potencia de la señal recibida se desconecta como\(1/d^{3}\).

Solución

Tenga en cuenta que la señal se cae más rápido que la\(1/d^{2}\) variación del espacio libre. No es suficiente conocer la potencia total transmitida y en su lugar se debe conocer la densidad de potencia a una distancia determinada. La potencia recibida de manera confiable,\(P_{R}\) (\(5\text{ km}\)), at\(5\text{ km}\) es\(100\text{ nW}\) y esta es la densidad de potencia,\(P_{D}\) (\(5\text{ km}\)), multiplicada por el área efectiva\(A_{r}\),, de la antena receptora:

\[P_{R}\:(5\text{ km})=100\text{ nW}=P_{D}\: (5\text{ km})A_{r}=\frac{k}{d^{3}}=\frac{k}{(5\text{ km})^{3}}=\frac{k}{125\text{ km}^{3}}\nonumber \]

Ambos\(A_{r}\) y\(k\) son constantes y\(k = 12500\text{ nW}\cdot\text{km}^{3} = 1.25\cdot 10^{−5}\text{ W}\cdot\text{km}^{3}\). La potencia recibida a distancia\(d\) es\(1\text{ pW}\) cuando

\[\begin{align} P_{R}(d)&=1\text{ pW}=10^{-12}\text{ W}=\frac{k}{d^{3}}=\frac{1.25\times 10^{-5}\text{W}\cdot\text{km}^{3}}{d^{3}}\nonumber \\ \label{eq:2} d^{3}&=\frac{1.25\times 10^{-5}\text{ W}\times\text{km}^{3}}{10^{-12}\text{ W}}=1.25\times 10^{7}\text{ km}^{3};\quad d=\sqrt[3]{1.25\times 10^{7}}\text{ km}=232.1\text{ km}\end{align} \]

Descripción	Fórmula	Ejemplo
Equivalencia	\(y=\log_{b}(x)\longleftrightarrow x=b^{y}\)	\(\log (1000)=3\text{ and }10^{3}=1000\)
Producto	\(\log_{b}(xy)=\log_{b}(x)+\log_{b}(y)\)	\(\log (0.13\cdot 978)=\log (0.13)+\log (978)=-0.8861+2.990=2.104\)
Ratio	\(\log_{b}(x/y)=\log_{b}(x)-\log_{b}(y)\)	\(\ln (8/2)=\ln (8)-\ln (2)=3-1=2\)
Poder	\(\log_{b}(x^{p})=p\log_{b}(x)\)	\(\ln (3^{2})=2\ln (3)=2\cdot 1.0986=2.197\)
Raíz	\(\log_{b}(\sqrt[p]{x})=\frac{1}{p}\log_{b}(x)\)	\(\log (\sqrt[3]{20})=\frac{1}{3}\log (20)=0.4337\)
Cambio de base	\(\log_{b}(x)=\frac{\log_{k}(x)}{\log_{k}(b)}\)	\(\ln (100)=\frac{\log (100)}{\log (2)}=\frac{2}{0.30103}=6.644\)

Cuadro\(\PageIndex{1}\): Fórmulas de logaritmos comunes. En ingeniería\(\log x ≡ \log_{10} x\) y\(\ln x ≡ \log_{2} x\)

1.6.2 Logaritmo

Un teléfono celular puede recibir de manera confiable una señal tan pequeña como\(100\text{ fW}\) y la señal a transmitir podría ser\(1\text{ W}\). Entonces el mismo circuito puede encontrar señales que difieren en potencia por un factor de\(10^{13}\). Para manejar un rango tan grande de señales se usa una escala logarítmica.

Los logaritmos se utilizan en ingeniería de RF para expresar la relación de potencias usando números razonables. Los logaritmos se toman con respecto a una base\(b\) tal que si\(x = b^{y}\), entonces\(y = \log_{b}(x)\). En ingeniería,\(\log (x)\) es lo mismo que\(\log_{10}(x)\), y\(\ln (x)\) es lo mismo que\(\log_{e}(x)\) y se llama logaritmo natural\((e = 2.71828\ldots)\). Desafortunadamente en física y matemáticas (y en programas como MATLAB),\(\log x\) significa\(\ln x\), así que ten cuidado. Las fórmulas comunes que involucran logaritmos se dan en la Tabla\(\PageIndex{1}\).

1.6.3 Decibelios

Los niveles de señal de RF generalmente se expresan en términos de la potencia de una señal. Si bien la potencia se puede expresar en términos absolutos como watts (\(\text{W}\)) o miliwatts (\(\text{mW}\)), es mucho más útil usar una escala logarítmica. La relación entre dos niveles de potencia\(P\) y\(P_{\text{REF}}\) en bels\(^{1}\) (\(\text{B}\)) es

\[\label{eq:3}P(B)=\log\left(\frac{P}{P_{\text{REF}}}\right) \]

donde\(P_{\text{REF}}\) es una potencia de referencia. Aquí\(\log x\) es lo mismo que\(\log_{10} x\). Los sentidos humanos tienen una respuesta logarítmica y la resolución mínima tiende a ser sobre\(0.1\text{ B}\), por lo que es más común usar decibelios (\(\text{dB}\));\(1\text{ B} = 10\text{ dB}\). Las designaciones comunes se muestran en la Tabla\(\PageIndex{2}\). También,\(1\text{ mW} = 0\text{ dBm}\) es un nivel de potencia muy común en los circuitos de potencia de RF y microondas donde el\(\text{m}\) in\(\text{dBm}\) se refiere a la\(1\text{ mW}\) referencia. Además,\(\text{dBW}\) se utiliza, y esta es la relación de potencia con respecto a\(1\text{ W}\) con\(1\text{ W} = 0\text{ dBW} = 30\text{ dBm}\).

Trabajar en la escala de decibelios permite cálculos convenientes utilizando números de potencia que van desde\(10\) s de\(\text{dBm}\)\(−110\text{ dBm}\) a ser utilizados en lugar de números que van desde\(100\text{ W}\) hasta\(0.00000000000001\text{ W}\).

\(P_{\text{REF}}\)	Unidades de campana	Unidades de decibelios
\ (P_ {\ texto {REF}}\) ">\(1\text{ W}\)	\(\text{BW}\)	\(\text{dBW}\)
\ (P_ {\ texto {REF}}\) ">\(1\text{ mW} = 10^{-3}\text{ W}\)	\(\text{Bm}\)	\(\text{dBm}\)
\ (P_ {\ texto {REF}}\) ">\(1\text{ fW} = 10^{-15}\text{ W}\)	\(\text{Bf}\)	\(\text{dBf}\)

Tabla\(\PageIndex{2}\) a: Designaciones de potencia común (a) Potencia de referencia,\(P_{\text{REF}}\)

Relación de potencia	en\(\text{dB}\)
\(10^{-6}\)	\ (\ texto {dB}\) ">\(-60\)
\(0.001\)	\ (\ texto {dB}\) ">\(-30\)
\(0.1\)	\ (\ texto {dB}\) ">\(-20\)
\(1\)	\ (\ texto {dB}\) ">\(0\)
\(10\)	\ (\ texto {dB}\) ">\(10\)
\(1000\)	\ (\ texto {dB}\) ">\(30\)
\(10^{6}\)	\ (\ texto {dB}\) ">\(60\)

Tabla\(\PageIndex{2}\) b: Designaciones de potencia comunes (b) Relaciones de potencia en decibelios (\(\text{dB}\))

Poder	Poder absoluto
\(-120\text{ dBM}\)	\(10^{-12}\text{ mW} = 10^{-15}\text{ W} = 1\text{ fW}\)
\(0\text{ dBm}\)	\(1\text{ mW}\)
\(10\text{ dBm}\)	\(10\text{ mW}\)
\(20\text{ dBm}\)	\(100\text{ mW} = 0.1\text{ W}\)
\(30\text{ dBm}\)	\(1000\text{ mW} = 1\text{ W}\)
\(40\text{ dBm}\)	\(10^{4}\text{ mW} = 10\text{ W}\)
\(50\text{ dBm}\)	\(10^{5}\text{ mW} = 100\text{ W}\)
\(-90\text{ dBm}\)	\(10^{-9}\text{ mW} = 10^{-12}\text{ W} = 1\text{ pW}\)
\(-60\text{ dBm}\)	\(10^{-6}\text{ mW} = 10^{-9}\text{ W} = 1\text{ nW}\)
\(-30\text{ dBm}\)	\(0.001\text{ mW} = 1\:\mu\text{W}\)
\(-20\text{ dBm}\)	\(0.01\text{ mW} = 10\:\mu\text{W}\)
\(-10\text{ dBm}\)	\(0.1\text{ mW} = 100\:\mu\text{W}\)

Tabla\(\PageIndex{2}\) c: Designaciones de potencia común (c) Potencias en\(\text{dBm}\) y vatios

Ejemplo\(\PageIndex{3}\): Power Gain

Un amplificador tiene una ganancia de potencia de\(1200\). ¿Cuál es la ganancia de poder en decibelios? Si la potencia de entrada es\(5\text{ dBm}\), ¿en qué se encuentra la potencia de salida\(\text{dBm}\)?

Solución

Ganancia de poder en decibelios,\(G_{\text{dB}} = 10 \log 1200 = 30.79\text{ dB}\).

La potencia de salida es\(P_{\text{out|dBm}} = P_{\text{dB}} + P_{\text{in|dBm}} = 30.79 + 5 = 35.79\text{ dBm}\).

Ejemplo\(\PageIndex{4}\): Gain Calculations

Una señal con una potencia de\(2\text{ mW}\) se aplica a la entrada de un amplificador que aumenta la potencia de la señal en un factor de\(20\).

Figura\(\PageIndex{1}\)

1. ¿En qué se encuentra la potencia de entrada\(\text{dBm}\)?
   \[\label{eq:4}P_{\text{in}}=2\text{ mW} = 10\cdot\log\left(\frac{2\text{ mW}}{1\text{ mW}}\right) = 10\cdot\log (2) = 3.010\text{ dBm}\approx 3.0\text{ dBm} \]
2. ¿Cuál es la ganancia\(G\),, del amplificador en\(\text{dB}\)?
   La ganancia del amplificador (por defecto esto es ganancia de potencia) es
   \[\label{eq:5}G=20=10\cdot\log (20)\text{ dB}=10\cdot 1.301\text{ dB}=13.0\text{ dB} \]
3. ¿Cuál es la potencia de salida del amplificador?
   \[\label{eq:6}G=\frac{P_{\text{out}}}{P_{\text{in}}},\quad\text{and in decibels }G|_{\text{dB}}=P_{\text{out}}|_{\text{dBm}}-P_{\text{in}}|_{\text{dBm}} \]
   Así la potencia de salida en\(\text{dBm}\) es
   \[\label{eq:7}P_{\text{out}}|_{\text{dBm}}=G|_{\text{dB}}+P_{\text{in}}|_{\text{dBm}}=13.0\text{ dB} +3.0\text{ dBm} =16.0\text{ dBm} \]
   Tenga en cuenta que\(\text{dB}\) y\(\text{dBm}\) son adimensionales pero sí tienen significado;\(\text{dB}\) indica una relación de potencia pero\(\text{dBm}\) se refiere a una potencia. Las cantidades en\(\text{dB}\) y una cantidad en se\(\text{dBm}\) pueden sumar o restar para producir\(\text{dBm}\), y la diferencia de dos cantidades en\(\text{dBm}\) rinde una relación de potencia en\(\text{dB}\).

Ejemplo\(\PageIndex{5}\): Power Calculations

La etapa de salida de un front-end RF consiste en un amplificador seguido de un filtro y luego una antena. El amplificador tiene una ganancia de\(33\text{ dB}\), el filtro tiene una pérdida de\(2.2\text{ dB}\), y de la entrada de potencia a la antena,\(45\%\) se pierde como calor debido a pérdidas resistivas. Si la entrada de energía al amplificador es\(1\text{ W}\), entonces:

Figura\(\PageIndex{2}\)

1. ¿En qué se expresa la entrada de potencia al amplificador\(\text{dBm}\)?
   \(P_{\text{in}}=1\text{ W}=1000\text{ mW},\quad P_{\text{dBm}}=10\log (1000/1)=30\text{ dBm}\)
2. Expresar la pérdida de la antena en\(\text{dB}\).
   \(45\%\)de la entrada de energía a la antena se disipa como calor.
   La antena tiene una eficiencia,\(\eta\), de\(55\%\) y así\(P_{2} = 0.55P_{1}\).
   \(\text{Loss} = P_{1}/P_{2} = 1/0.55 = 1.818 = 2.60\text{ dB}\).
3. ¿Cuál es la ganancia total del front-end de RF (amplificador + filtro + antena)?
   \[\begin{align}\text{Total gain }&= (\text{amplifier gain})_{\text{dB}}+(\text{filter gain})_{\text{dB}}-(\text{loss of antenna})_{\text{dB}}\nonumber \\ \label{eq:8}&=(33-2.2-2.6)\text{ dB}=28.2\text{ dB}\end{align} \]
4. ¿Cuál es la potencia total irradiada por la antena\(\text{dBm}\)?
   \[\begin{align}P_{r}&=P_{\text{in|dBm}}+(\text{amplifier gain})_{\text{dB}}+(\text{filter gain})_{\text{dB}}-(\text{loss of antenna})_{\text{dB}}\nonumber \\ \label{eq:9} &=30\text{ dBm}+(33-2.2-2.6)\text{ dB}=58.2\text{ dBm}\end{align} \]
5. ¿Cuál es la potencia total irradiada por la antena?
   \[\label{eq:10}P_{R}=10^{58.2/10}=(661\times 10^{3})\text{ mW}=661\text{ W} \]

En Ejemplos\(\PageIndex{3}\) y\(\PageIndex{4}\) dos dígitos siguientes al punto decimal se utilizaron para la potencia de salida expresada en\(\text{dBm}\). Esto corresponde a una precisión implícita de aproximadamente\(0.01\%\) o dígitos\(4\) significativos del número absoluto. Este nivel de precisión es típico para el resultado de un cálculo de ingeniería. Consulte la Sección 2.A.1 de [1] para mayor discusión de precisión y exactitud.

1.6.4 Decibelios y Ganancia de Voltaje

La Figura\(\PageIndex{3}\) (a) es un amplificador con resistencias de entrada y salida que podrían ser diferentes. Si\(A_{v}\) es la ganancia de voltaje del amplificador de RF, entonces

\[\label{eq:11}V_{2}=A_{v}V_{1} \]

y las potencias de entrada y salida serán

\[\label{eq:12}P_{\text{in}}=\frac{V_{1}^{2}}{2R_{1}}\quad\text{and}\quad P_{\text{out}}=\frac{V_{2}^{2}}{2R_{2}} \]

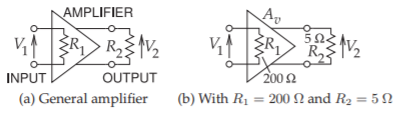
Figura\(\PageIndex{3}\): Amplificadores cada uno con una resistencia de entrada\(R_{1}\) y resistencia de salida\(R_{2}\).

El '\(2\)' en el denominador surge porque\(V_{1}\) y\(V_{2}\) son amplitudes pico de sinusoides en ingeniería de RF. Por lo tanto, la ganancia de poder es

\[\label{eq:13}G=\frac{P_{\text{out}}}{P_{\text{in}}}=\frac{V_{2}^{2}2R_{1}}{V_{1}^{2}2R_{2}}=\frac{R_{1}}{R_{2}}A_{v}^{2} \]

La ganancia de potencia depende de la relación de resistencia de entrada y salida de los amplificadores y esto se usa comúnmente para lograr una ganancia de potencia significativa incluso si la ganancia de voltaje es bastante pequeña. Si las resistencias de entrada y salida del amplificador son las mismas, entonces la ganancia de potencia es solo la ganancia de voltaje al cuadrado.

En el manejo de esta situación algunos autores han utilizado la unidad\(\text{dBV}\) (decibelios como relación de voltaje). Esto no debe usarse, los decibelios siempre deben referirse a una relación de potencia, y es innecesariamente confuso usar\(\text{dBV}\) en ingeniería de RF.

Ejemplo\(\PageIndex{6}\): Voltage Gain to Power Gain

La Figura\(\PageIndex{3}\) (b) es un amplificador diferencial con una resistencia\(200\:\Omega\) de entrada y una resistencia\(5\:\Omega\) de salida. Si el voltaje\(A_{v}\) es\(0.6\), ¿en qué se encuentra la ganancia de potencia del amplificador\(\text{dB}\)?

Solución

Las potencias de entrada y salida son

\[\label{eq:14}P_{\text{in}}=\frac{1}{2}V_{1}^{2}/R_{1}\quad\text{and}\quad P_{\text{out}}=\frac{1}{2}V_{2}^{2}/R_{2}=\frac{1}{2}\frac{(A_{v}V_{1})^{2}}{R_{2}} \]

Por lo tanto, la ganancia de poder es

\[\label{eq:15} G=\frac{P_{\text{out}}}{P_{\text{in}}}=\frac{(A_{v}V_{1})^{2}}{R_{2}}\left(\frac{V_{1}^{2}}{R_{1}}\right)^{-1}=\frac{R_{1}}{R_{2}}A_{v}^{2}=\frac{200}{5}0.6^{2}=14.4=11.58\text{ dB} \]

El resultado sorprendente es que incluso con una ganancia de voltaje inferior a\(1\), se puede obtener una ganancia de potencia significativa si las resistencias de entrada y salida son diferentes. Un resultado utilizado en muchos amplificadores de RF.

Notas al pie

[1] Nombrado para honrar a Alexander Graham Bell, un prolífico inventor y contribuyente importante a las comunicaciones de RF.