2.13: Modulación por Desplazamiento de Fase

Hay muchas variaciones en la modulación por desplazamiento de fase (PSK) con los métodos que difieren por sus eficiencias espectrales, PMEPR e idoneidad para la recuperación de portadoras. En comparación con FSK, se requiere un procesamiento de señal digital más sofisticado para demodular una señal modulada por PSK.

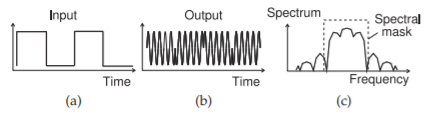
Figura\(\PageIndex{1}\): Modulación PSK binaria: (a) flujo de bits de modulación; (b) la forma de onda modulada; y (c) su espectro después de suavizar las transiciones de un estado de fase a otro.

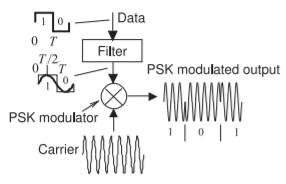
Figura\(\PageIndex{2}\): Un sistema de modulación por desplazamiento de fase binaria (PSK).

2.8.1 Esenciales de PSK

PSK es un esquema de modulación digital eficiente y puede implementarse y demodularse simplemente usando un bucle de bloqueo de fase. El esquema más simple es PSK binario (BPSK) con dos estados de fase. La forma de onda y el espectro de BPSK se muestran en la Figura\(\PageIndex{2}\). El flujo de bits de banda base entrante mostrado en la Figura\(\PageIndex{1}\) (a) modula la fase de una portadora que produce la señal modulada mostrada en la Figura\(\PageIndex{1}\) (b). El espectro de la señal modulada se muestra en la Figura\(\PageIndex{1}\) (c). Lo que es muy interesante de este espectro es que aproximadamente llena un cuadrado. Entonces, la modulación PSK da como resultado un uso eficiente del espectro. Esto se puede contrastar con el espectro de una señal FM mostrada en la Figura 2.4.5 (c), que no llena el canal de manera uniforme. Un sistema de modulación PSK binario se muestra en la Figura\(\PageIndex{2}\) donde los datos binarios de entrada provocan cambios de\(180^{\circ}\) fase de la portadora. Los cambios bruscos de fase mostrados en la forma de onda modulada de salida dan como resultado más ancho de banda del necesario. Sin embargo, un modulador PSK práctico primero filtra los datos binarios antes de que se modula la portadora. Este filtrado elimina los cambios bruscos en la fase de la señal modulada y así reduce el ancho de banda requerido. Es el espectro de esta señal el que se muestra en la Figura\(\PageIndex{1}\) (c).

Existen muchas variantes de complejidad creciente, llamadas órdenes, de PSK, siendo las características fundamentales el número de estados de fase (por ejemplo, con estados de\(2^{n}\) fase, se pueden transmitir\(n\) bits de información) y cómo el fasor de la señal RF pasa de un estado de fase a otro. Los esquemas PSK están diseñados para dar forma al espectro de la señal modulada para ajustarse a la mayor cantidad de energía posible dentro de una máscara espectral. Esto da como resultado una portadora modulada cuya amplitud varía (y por lo tanto tiene una envolvente variable en el tiempo). Tales esquemas requieren amplificadores altamente lineales para preservar las variaciones de amplitud de la señal de RF modulada.

Existen métodos PSK que gestionan las transiciones de fase para lograr una señal de RF modulada en envolvente constante pero estos tienen menor eficiencia espectral. Las radios militares a veces utilizan este tipo de esquema de modulación ya que es mucho más difícil detectar e interceptar comunicaciones si la amplitud de la portadora modulada es constante.

El límite de comunicación de un símbolo por hercio de ancho de banda,

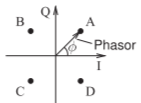
Figura\(\PageIndex{3}\): Diagrama fasor de modulación QPSK. Aquí hay cuatro estados de fase discretos del fasor indicados por los puntos A, B, C y D. El modulador PSK mueve el fasor de un estado de fase a otro. La tarea en el receptor es determinar la fase del fasor.

la tasa de símbolos, proviene del teorema de señalización Nyquist. \(^{1}\)Nyquist determinó que el número de pulsos independientes que podrían ser puestos a través de un canal telegráfico por unidad de tiempo está limitado al doble del ancho de banda del canal. Con una portadora de RF modulada, esto se traduce en que la portadora modulada se mueve de un estado a otro en una unidad de tiempo igual a una sobre el ancho de banda. La transición identifica un símbolo y, por lo tanto, se puede enviar un símbolo por hercios de ancho de banda. Con mayor precisión se podría decir que la transición es un símbolo más que el final de la transición es un símbolo. En la modulación PSK los estados son las fases de un fasor ya que la amplitud de la señal modulada es (idealmente) constante.

La portadora desfasada (es decir, modulada en fase) de una señal PSK se puede representar en un diagrama de fase. La figura\(\PageIndex{3}\) es un diagrama de fasores con cuatro estados de fase (a, B, C, D) y el fasor se mueve de un estado a otro bajo el control del circuito de modulación. Lo que se muestra aquí es PSK de 4 estados o modulación por desplazamiento de fase cuadra (QPSK) y muy a menudo pero con menor precisión se llama modulación por desplazamiento de fase en cuadratura. Los estados, o símbolos, se identifican por su ángulo o equivalentemente por sus coordenadas rectangulares, llamadas I, para en fase, y Q, para fase en cuadratura.

Modulación PSK

En la modulación PSK, la fase de una señal portadora se establece en uno de varios valores discretos en las garrapatas de reloj. Por ejemplo, en QPSK hay cuatro ajustes discretos de la fase de la portadora, por ejemplo\(45^{\circ},\: 135^{\circ},\: −135^{\circ},\) y\(−45^{\circ}\). Al convertir esto en radianes, la señal de banda base discreta es\(\phi (t) = π/4,\: 3π/4,\: 5π/4,\) y\(7π/4\), en las garrapatas del reloj. Así, si el ancho de banda de la señal de banda base es\(1\text{ MHz}\) lo que se muestra como\(\phi(t)\) son las fases previstas de la portadora cada microsegundo. La conformación de onda o el filtrado se utiliza para proporcionar una variación suave de\(\phi(t)\) entre las garrapatas del reloj y así el ancho de banda de la señal modulada está restringido. La modulación PSK de orden superior tiene estados más discretos, por ejemplo, 8-PSK tiene ocho estados de fase discretos.

Hay varias formas de implementar la modulación PSK y una usa el modulador en cuadratura que se muestra en la Figura\(\PageIndex{4}\). La señal de banda base discreta\(\phi(t)\) podría ser interna a un DSP que luego es interpolado en el tiempo y enviado por el DAC del DSP como dos señales suaves\(i(t) = \cos(\phi(t))\) y\(q(t) = \sin(\phi(t))\). En un diagrama de fasores\(i(t)\) y\(q(t)\) en las garrapatas del reloj se dirige a uno de los cuatro estados de QPSK del fasor del portador, ver Figura\(\PageIndex{3}\).

Para la modulación PSK, el diagrama de constelación es muy similar a un diagrama fasor que se vuelve a normalizar continuamente a la potencia promedio de

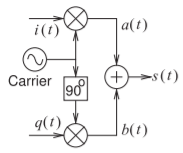
Figura\(\PageIndex{4}\): Diagrama de bloques del modulador en cuadratura. En modulación\(i(t)\) PSK\(q(t)\) ya tienen la misma amplitud e indican una fase\(\phi\) de la portadora modulada para que\(i(t) = \cos[\phi(t)]\) y\(q(t) = \sin[\phi(t)]\). El ejemplo particular muestra dos valores posibles de\(I_{k}\) y\(Q_{k}\) y esto indica modulación QPSK.

la señal modulada. Esta es una distinción sutil pero importante, por ejemplo, una señal de banda base PSK tiene un diagrama de constelación aunque la señal de banda base no tenga una representación fasorial. La modulación PSK usando el diagrama de bloques que se muestra en la Figura\(\PageIndex{4}\) tiene una portadora que se introduce directamente en el multiplicador superior y una versión\(90^{\circ}\) desplazada en fase de entrada al multiplicador inferior. Deje que el portador sea\(\cos(\omega_{c}t)\) y así la versión de la entrada del portador al multiplicador inferior es\(\cos(\omega_{c}t − π/2) = −\sin(\omega_{c}t)\). Entonces, con\(q(t)\) ser una versión\(90^{\circ}\) desplazada de fase de\(i(t)\), (usando las identidades en la Sección 1.A.2 de [4]).

\[\begin{align}\label{eq:1}a(t)&=\cos(\phi(t))\cos(\omega_{c}t)=\frac{1}{2}\left[\cos(\omega_{c}t-\phi(t))+\cos(\omega_{c}t+\phi(t))\right] \\ \label{eq:2}b(t)&=\sin(\phi(t))\left[-\sin(\omega_{c}t)\right]=-\frac{1}{2}\left[\cos(\omega_{c}-\phi(t))-\cos(\omega_{c}t+\phi(t))\right] \\ \label{eq:3}s(t)&=a(t)+b(t)=\cos(\omega_{c}t+\phi(t))\end{align} \]

Así\(s(t)\) es la portadora modulada de banda lateral única que transporta información en la fase de la portadora modulada. La señal moduladora\(\phi(t)\) es impulsada por un código digital que está diseñado para que\(\phi(t)\) cambie a una tasa mínima (nunca tiene el mismo valor por más de unas pocas garrapatas de reloj). Por lo tanto, no hay componentes de baja frecuencia\(\phi(t)\) y, por lo tanto, no hay señal modulada en o muy cerca de la portadora. Por lo tanto, la portadora se suprime pero hay una banda lateral por encima y por debajo de la frecuencia portadora. Esta es la modulación SSB-SC.

2.8.2 Modulación por desplazamiento de fase binaria

PSK utiliza desplazamientos de fase prescritos para definir símbolos, cada uno de los cuales puede representar uno, dos o más bits. Binary Phase Shift Keying (BPSK), ilustrado en las Figuras\(\PageIndex{1}\) y\(\PageIndex{2}\), tiene dos estados de fase y transmite un bit por símbolo y es un esquema relativamente espectralmente ineficiente, con una eficiencia de modulación máxima (es decir, ideal) de\(1\text{ bits/s/Hz}\). La razón por la que la eficiencia de modulación práctica es menor que este número es porque la transición de un estado de fase al otro debe restringirse para evitar que la señal modulada se vuelva muy pequeña, y también porque no hay filtros de paso bajo ideales para filtrar el flujo de datos binarios de entrada. Aunque tiene una baja eficiencia de modulación, es ideal para aplicaciones de baja potencia. BPSK se usa comúnmente en Bluetooth.

El funcionamiento de la modulación BPSK puede describirse usando el diagrama de constelación mostrado en la Figura\(\PageIndex{5}\) (a). El diagrama de constelación BPSK indica que hay dos estados. Estos estados pueden interpretarse como los valores rms de\(i(t)\) y\(q(t)\) en los tiempos de muestreo correspondientes a la tasa de bits. La distancia de un punto de constelación desde el origen corresponde a la potencia rms (normalizada) de la pseudo-sinusoide de la portadora modulada en el instante de muestreo. (La normalización es con respecto a la potencia promedio.) Las curvas de la Figura\(\PageIndex{5}\) (b) indican tres transiciones. Los estados están al final de las transiciones. Si a\(1\), en la Figura\(\PageIndex{5}\) (b), se le asigna al\(I\) valor positivo y\(0\)

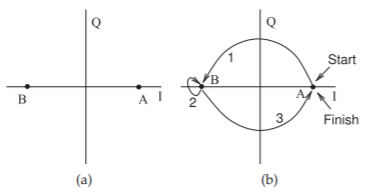
Figura\(\PageIndex{5}\): Modulación BPSK con puntos de constelación A y B: (a) diagrama de constelación; y (b) diagrama de constelación con posibles transiciones de un estado de fase a otro, o posiblemente ningún cambio en el estado de fase. En sistemas prácticos la transición no debe pasar por el origen, ya que entonces la señal de RF caería por debajo del nivel de ruido.

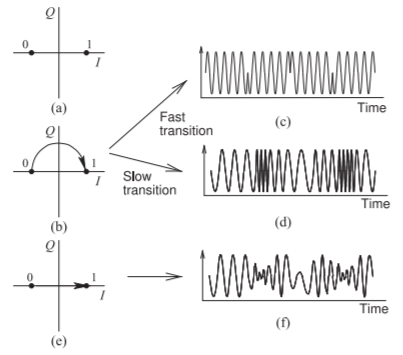
Figura\(\PageIndex{6}\): Modulación BPSK: (a) diagrama de constelación; (b) diagrama de constelación con una transición de amplitud constante; (c) forma de onda en el dominio del tiempo si la transición es rápida; (d) forma de onda en el dominio del tiempo si la transición es lenta; (e) diagrama de constelación con transición a través del origen; y (f) dominio del tiempo forma de onda si la transición pasa por el origen y es lenta.

a un\(I\) valor negativo, entonces la secuencia de bits representada en la Figura\(\PageIndex{5}\) (b) es “\(1001\).”

La Figura\(\PageIndex{6}\) (a) es el diagrama de constelación de BPSK, con dos símbolos denotados como\(0\) y\(1\), y la trayectoria de la transición de un punto de constelación a otro dependiendo del hardware utilizado para implementar el modulador BPSK. La figura\(\PageIndex{6}\) (b) muestra la transición del estado\(0\) '' al estado '\(1\)' (y atrás) mientras se mantiene una amplitud constante. Si esta transición es muy rápida, entonces la forma de onda producida es como se muestra en la Figura\(\PageIndex{6}\) (c), donde hay transiciones de fase abruptas y éstas tienen un alto contenido espectral. Es mejor ralentizar las transiciones, ya que entonces la forma de onda (mostrada en la Figura\(\PageIndex{6}\) (d)), tiene transiciones suaves y el ancho de banda de la portadora modulada es mínimo. La transición suave preferida se obtiene filtrando paso bajo la señal de banda base. Es decir, las transiciones abruptas en la señal de RF modulada dan como resultado que la señal modulada tenga un ancho de banda amplio. La transición elegante de la modulación BPSK limita el ancho de banda de la portadora modulada.

Una implementación simple de la modulación BPSK resultaría en una transición directa de un estado a otro haciendo que el fasor atraviese el origen y la amplitud de la señal de RF se volviera muy pequeña y menor que el nivel de ruido (ver Figura\(\PageIndex{6}\) (e)). La forma de onda de RF modulada resultante es

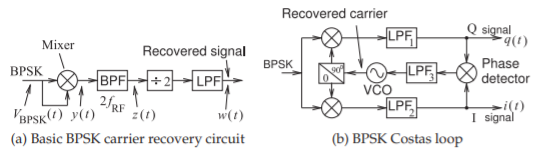
Figura\(\PageIndex{7}\): Diagrama de bloques de circuitos de recuperación de portadora para señales BPSK.

que se muestra en la Figura\(\PageIndex{6}\) (f). Esto es un problema porque el receptor no podría rastrear la señal de RF.

Recuperación de Carrier

En un demodulador PSK, se debe producir una copia local de la portadora para que actúe como referencia en la determinación de la fase de la señal modulada. La técnica que produce la copia local de la portadora no modulada se denomina recuperación de portadora. El circuito que implementa directamente la recuperación de portadora de una señal BPSK se muestra en la Figura\(\PageIndex{7}\) (a). En las garrapatas del reloj, la forma de onda de una señal modulada BPSK es

\[\label{eq:4}v_{\text{BPSK}}(t)=A(t)\cos(\omega_{\text{RF}}t+n\pi ) \]

donde la frecuencia portadora\(f_{\text{RF}} = \omega_{\text{RF}}/(2π)\) y\(n\) puede tener un valor de\(0\) o\(1\). Al cuadrar esto produce una señal

\[\begin{align}y(t)=v_{\text{BPSK}}^{2}(t)&=A^{2}(t)\cos^{2}(\omega_{\text{RF}}t+n\pi)=\frac{1}{2}A^{2}(t)[1+\cos(2\omega_{\text{RF}}t+n2\pi )]\nonumber \\ \label{eq:5}&=\frac{1}{2}A^{2}(t)[1+\cos(2\omega_{\text{RF}}t)]\end{align} \]

Esta es una señal al doble de la frecuencia portadora sin modulación portadora ya que\(n2π\) y\(0\) los radianes son indistinguibles. La operación de cuadratura se realiza mezclando\(v_{\text{BPSK}}(t)\) consigo mismo. El filtrado de paso de banda\(y(t)\) produce una señal\(z(t)\) en el segundo armónico de la portadora. El bloque de división por 2 se implementa usando un bucle de bloqueo de fase (PLL). El resultado es la portadora recuperada\(w(t)\), que se utiliza como referencia de temporización para muestrear los componentes I y Q demodulados en momentos precisos.

Un mejor circuito de recuperación de portadora que el de la Figura\(\PageIndex{7}\) (a) y descrito anteriormente es el bucle Costas [14] mostrado en la Figura\(\PageIndex{7}\) (b). El bucle BPSK Costas implementa la recuperación de portadora y la demodulación I/Q simultáneamente. En la Figura\(\PageIndex{7}\) (b)\(i(t)\) y\(q(t)\) se mezclan para producir una señal aplicada a la entrada del tercer filtro de paso bajo,\(\text{LPF}_{3}\). La función principal de este filtro es eliminar el ruido y promediar la señal que sale del detector de fase. La salida de\(\text{LPF}_{3}\) impulsa un VCO en el que la frecuencia de oscilación es controlada por el voltaje aplicado. El desplazador de fase en cuadratura mezcla entonces la portadora recuperada y una versión\(90^{\circ}\) desplazada con la señal BPSK.

Es crítico que la relación señal/ruido (SNR), la relación entre la potencia de la señal y la potencia de ruido, de la señal BPSK sea suficientemente grande en todo momento o bien el bucle Costas producirá una señal portadora recuperada ruidosa. Si la portadora modulada se vuelve muy pequeña, por ejemplo cuando la trayectoria en el diagrama de constelación pasa por el origen (donde el nivel de la portadora portadora cae por debajo del nivel de ruido), la portadora no se recuperará con precisión.

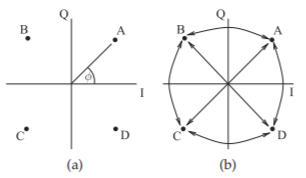
Figura\(\PageIndex{8}\): Modulación QPSK: (a) diagrama de constelación; y (b) diagrama de constelación con posibles transiciones. Cada punto de constelación indica la fase,\(\phi\), de la portadora modulada, es decir,\(\cos(\omega_{c}t + \phi)\) dónde\(\omega_{c}\) está la frecuencia de radianes de la portadora.

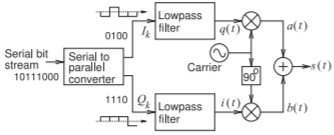
Figura\(\PageIndex{9}\): Diagrama de bloques del modulador QPSK. \(I_{k}\)y\(Q_{k}\) son similares a un flujo de señales binarias de un bit pero son analógicas con un valor positivo o un voltaje negativo de modo que después del filtrado paso bajo\(i(t)\) y\(q(t)\) cada uno tenga un voltaje positivo o negativo en cada tick de reloj.

2.8.3 Modulación por desplazamiento de fase cuatrifásica, QPSK

En los sistemas inalámbricos QPSK, la eficiencia de modulación se obtiene enviando más de un bit de información por hertz de ancho de banda (es decir, más de un bit por símbolo). En QPSK la información se codifica en cuatro estados de fase y se requieren dos bits para identificar un símbolo (es decir, para identificar un estado de fase). El diagrama de constelación de QPSK se muestra en la Figura\(\PageIndex{8}\) (a) donde la portadora de RF modulada tiene cuatro estados de fase identificados como A, B, C y D. Así que un modulador QPSK desplaza la fase de la portadora a uno de estos estados de fase, y un demodulador QPSK debe determinar la fase de la señal RF recibida. La señal RF recibida se muestrea con una temporización precisa según lo determinado por la señal portadora recuperada. Así, se transmiten dos bits de información por cambio de estados de fase. Cada cambio de estado de fase requiere al menos\(1\text{ Hz}\) de ancho de banda con el ancho de banda mínimo obtenido cuando la transición de un estado a otro no es más rápida que la requerida para alcanzar el nuevo estado de fase antes del instante de muestreo. La modulación QPSK también se conoce como PSK cuarteraria.

QPSK se puede implementar usando el modulador mostrado en la Figura\(\PageIndex{9}\). En la Figura\(\PageIndex{9}\), el flujo de bits de entrada se convierte primero en dos flujos de bits paralelos que contienen cada uno la mitad del número de bits del flujo de bits original. Así, una secuencia de dos bits en el flujo de bits en serie se convierte en un\(I_{K}\) bit y un\(Q_{K}\) bit. El\((I_{K}, Q_{K})\) par constituye el símbolo\(K\) th. Los flujos de bits son convertidos en formas de onda\(i(t)\) y\(q(t)\) por el circuito de conformación de onda.

El diagrama de constelación de QPSK es el resultado de trazar\(I\) y\(Q\) en un gráfico rectangular como se muestra en la Figura\(\PageIndex{8}\) (a). Todas las transiciones de fase posibles se muestran en la Figura\(\PageIndex{8}\) (b). En ausencia de circuitos de conformación de onda,\(i(t)\) y\(q(t)\) tienen transiciones muy nítidas, y las trayectorias mostradas en la Figura\(\PageIndex{5}\) (b) ocurren casi instantáneamente. Esto conduce a grandes extensiones espectrales en la forma de onda modulada,\(s(t)\). Entonces, para limitar el espectro de la señal de RF\(s(t)\),\(q(t)\) se controla la forma de\(i(t)\) y; la forma de onda se forma, generalmente mediante filtrado de paso bajo. Entonces, un circuito de conformación de pulsos cambia la información binaria de banda base en una señal que varía más suavemente. Cada transición o ruta en la Figura\(\PageIndex{5}\) representa la transferencia de un símbolo, siendo la mejor eficiencia que se puede obtener en la comunicación inalámbrica un símbolo por hercio de ancho de banda. Cada símbolo contiene dos bits, por lo que la máxima eficiencia de modulación de la modulación QPSK es\(2\text{ bits/s/Hz}\) de ancho de banda. Lo que realmente se logra depende de los circuitos de conformación de onda y de los criterios utilizados para establecer el ancho de banda de\(s(t)\).

Recuperación de Carrier

La recuperación de portadora de una señal QPSK es similar a la de una señal BPSK. En el reloj marca una señal modulada RF QPSK

\[\label{eq:6}v_{\text{QPSK}}(t)=A(t)\cos (\omega_{\text{RF}}t+n\pi /2);\quad n=0,1,2,3, \]

donde la frecuencia portadora\(f_{\text{RF}} = \omega_{\text{RF}}/(2π)\). El cuarto poder de esto produce

\[\begin{align}v_{\text{QPSK}}^{4}(t)&=A^{4}(t)\cos^{4}(\omega_{\text{RF}}t+n\pi /2)\nonumber \\ \label{eq:7}&=\frac{1}{8}A^{4}(t)[3+4\cos (2\omega_{\text{RF}}t+n\pi)+\cos(4\omega_{\text{RF}}t+n2\pi)]\end{align} \]

Después del filtrado de paso de banda en\(4f_{\text{RF}}\) y luego dividiendo la frecuencia por\(4\), se recupera la portadora. Los circuitos que implementan esto son similares a los de recuperar la portadora de señales BPSK. Este concepto se puede extender a la recuperación de portadoras para cualquier señal\(M\) modulada -PSK.

Ejemplo\(\PageIndex{1}\): QPSK Modulation and Constellation

La secuencia de bits\(\mathsf{110101001100}\) se va a transmitir usando modulación QPSK. Mostrar las transiciones en un diagrama de constelación.

Solución

La secuencia de bits\(\mathsf{110101001100}\) debe ser convertida en un flujo paralelo de dos bits de ancho de símbolos dando como resultado la secuencia de símbolos\(\mathsf{11 01 01 00 11 00}\). El símbolo\(\mathsf{11}\) pasa al símbolo\(\mathsf{01}\) y luego al símbolo\(\mathsf{01}\) y así sucesivamente. Los estados (o símbolos) y las transiciones de un símbolo al siguiente requeridos para enviar el flujo de bits se\(\mathsf{110101001100}\) muestran en la Figura\(\PageIndex{10}\). La modulación QPSK da como resultado que el fasor de la portadora pase por el origen de manera que la potencia promedio sea menor y el PMEPR sea alto. Un problema más significativo es que el fasor caerá por debajo del piso de ruido, haciendo casi imposible la recuperación del portador.

2.8.4 Modulación por desplazamiento de fase en\(\pi /4\) cuadratura

Un objetivo importante en la modulación digital es asegurar que la trayectoria de RF de un estado de fase a otro no pase por el origen. La transición es lenta, de manera que si la trayectoria pasa por el origen, la amplitud de la portadora estará por debajo del piso de ruido durante un tiempo considerable y no será posible recuperar la referencia de portadora. Es por ello que el esquema QPSK no se utiliza directamente en la radio celular 2G y 3G. (Los sistemas de radio celular 4G y 5G sí utilizan QPSK entre otros esquemas de modulación y utilizan tonos piloto para recuperar la portadora). Una de las soluciones desarrolladas para abordar este problema es el esquema de modulación por desplazamiento de fase en\(π/4\) cuadratura (\(π/4\)-QPSK). En este esquema la constelación en cada símbolo es girada\(π/4\) radianes del símbolo anterior, como se muestra en la Figura\(\PageIndex{11}\). (En una implementación alternativa de modulación\(π/4\) -QPSK, el diagrama de constelación podría

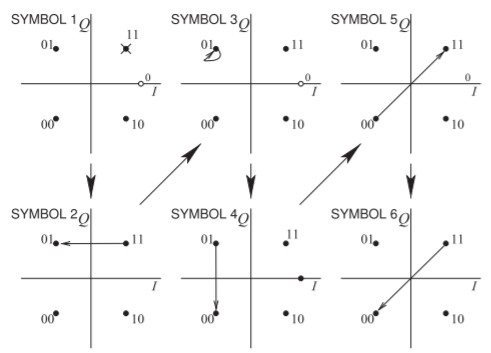
Figura\(\PageIndex{10}\): Diagrama de constelación y transiciones para la secuencia de bits\(\mathsf{110101001100}\) enviada como el conjunto de símbolos\(\mathsf{11 01 01 00 11 00}\) usando QPSK. Tenga en cuenta que los símbolos\(2\) y\(3\) son idénticos, por lo que no hay transición. Los\(\mathsf{SYMBOL}\) números indicados hacen referencia al símbolo al final de la transición (final de la flecha). La asignación de bits a símbolos (por ejemplo, asignar los bits '\(11\)' al símbolo en el primer cuadrante) es arbitraria en general pero la asignación de símbolos se define en un estándar particular.

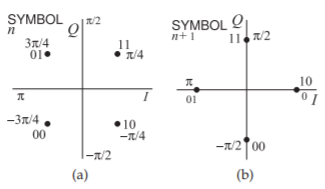
Figura\(\PageIndex{11}\): Diagrama de constelación de\(π/4\) - Modulación QPSK: (a) diagrama de constelación inicial en un símbolo; y (b) el diagrama de constelación en el momento del siguiente símbolo.

rotar\(π/4\) continuamente en lugar de cambiar entre condiciones como se describe aquí.)

Una de las características únicas de la modulación\(π/4\) -QPSK es que siempre hay un cambio, aunque se repita un símbolo. Esto ayuda a recuperar la frecuencia portadora. Si el flujo binario en sí mismo (con transiciones nítidas en el tiempo) es la señal de modulación, entonces la transición de un símbolo al siguiente ocurre instantáneamente y, por lo tanto, la señal modulada tiene un amplio espectro alrededor de la frecuencia portadora. La transición, sin embargo, es más lenta si se filtra el flujo de bits, y así el ancho de banda de la señal modulada será menor. Idealmente se obtendría la transmisión de un símbolo por hercio. Sin embargo, en la modulación\(π/4\) -QPSK el cambio de un símbolo al siguiente tiene una distancia variable (y así una transición toma diferentes tiempos) de manera que la eficiencia de modulación ideal de un símbolo por segundo por hercio (o\(2\)

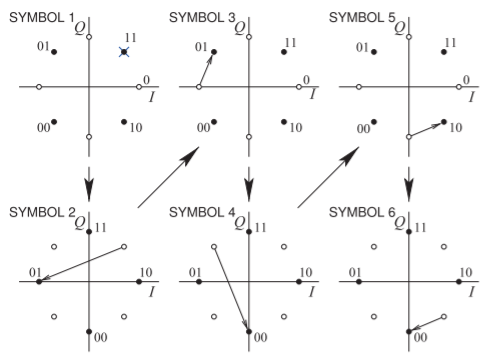
Figura\(\PageIndex{12}\): Estados del diagrama de constelación y transiciones para la secuencia de bits\(\mathsf{110101001000}\) enviada como el conjunto de símbolos\(\mathsf{11 01 01 00 10 00}\) usando modulación\(π/4\) QPSK.

\(\text{bits/s/Hz}\)) no se obtiene. En la práctica, con filtros realistas y permitiendo las transiciones más largas, la modulación\(π/4\) -QPSK logra\(1.62\text{ bits/s/Hz}\).

Ejemplo\(\PageIndex{2}\): \(\pi /4\)-QPSK Modulation and Constellation

La secuencia de bits\(\mathsf{110101001000}\) se transmite usando modulación\(π/4\) -QPSK. Mostrar las transiciones en un diagrama de constelación.

Solución

La secuencia de bits\(\mathsf{110101001000}\) debe convertirse en un flujo paralelo de símbolos de dos bits de ancho, dando como resultado la secuencia de símbolos\(\mathsf{11 01 01 00 10 00}\). El símbolo\(\mathsf{11}\) pasa al símbolo\(\mathsf{01}\) y luego al símbolo\(\mathsf{01}\) y así sucesivamente. El diagrama de constelación de modulación\(π/4\) -QPSK consiste realmente en dos diagramas de constelación QPSK que se desplazan por\(π/4\) radianes, como se muestra en la Figura\(\PageIndex{11}\). En un símbolo (o tiempo) el diagrama de constelación es el que se muestra en la Figura\(\PageIndex{11}\) (a) y en el siguiente símbolo es el que se muestra en la Figura\(\PageIndex{11}\) (b). El siguiente símbolo utiliza el diagrama de constelación de la Figura\(\PageIndex{11}\) (a) y el proceso se repite. Los estados (o símbolos) y las transiciones de un símbolo al siguiente que se requieren para enviar el flujo de bits se\(\mathsf{110101001000}\) muestran en la Figura\(\PageIndex{12}\).

2.8.5 Modulación por Desplazamiento de Fase Quadra Diferencial, DQPSK

Múltiples trayectorias de transmisión, o multipaths, debido a las reflexiones dan como resultado interferencias constructivas y destructivas y pueden resultar en rotaciones de fase adicionales rápidas. Por lo tanto, confiar en la fase de un fasor en el tiempo de muestreo del símbolo, en las garrapatas del reloj, para determinar el símbolo transmitido es propenso al error. Cuando un error resulta en un símbolo, este error se acumula cuando se extraen símbolos subsiguientes. La solución es usar codificación, y uno de los esquemas de codificación más simples es la codificación de fase diferencial. En este esquema la información de la señal modulada está contenida en cambios de fase más que en la fase absoluta. Es decir, la transición define el símbolo más que el punto final de la transición.

El esquema de modulación\(π/4\) -DQPSK es una forma codificada diferencialmente de

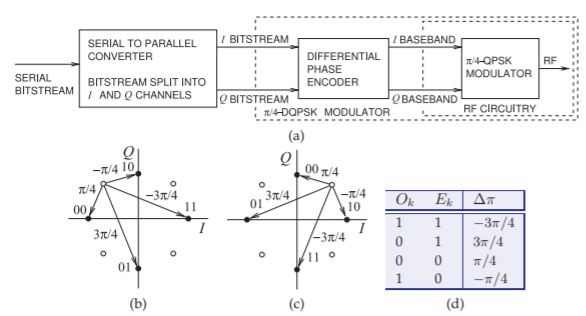
Figura\(\PageIndex{13}\): Un modulador\(π/4\) -DQPSK: (a) codificador de fase diferencial con un modulador\(π/4\) -QPSK; (b) diagrama de constelación de\(π/4\) -DQPSK; (c) un segundo diagrama de constelación; y (d) cambios de fase en un esquema de modulación\(π/4\) -DQPSK. Tenga en cuenta que la información está en el cambio de fase en lugar del estado de fase.

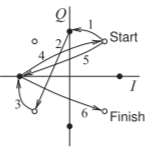
Figura\(\PageIndex{14}\): Diagrama de constelación de modulación\(π/4\) - DQPSK que muestra seis intervalos de símbolos que codifican la secuencia de bits\(\mathsf{000110110101}\).

\(π/4\)-QPSK. El esquema\(π/4\) -DQPSK incorpora el modulador\(π/4\) -QPSK y un esquema de codificación, como se muestra en la Figura\(\PageIndex{13}\) (a). El esquema se define con respecto a su diagrama de constelación, mostrado en la Figura\(\PageIndex{14}\) (b) y repetido en la Figura\(\PageIndex{13}\) (c) para mayor claridad. La D indica codificación diferencial, mientras que la\(π/4\) denota la rotación de la constelación por\(π/4\) radianes de un intervalo al siguiente. Esto puede explicarse considerando la Figura\(\PageIndex{13}\) (a). Un flujo de cuatro bits se divide en dos nibbles en cuadratura de dos bits cada uno. Estos bocados controlan independientemente el\(I\) y la\(Q\) codificación, respectivamente, de manera que las transiciones permitidas rotan de acuerdo con la última transición. La información o los datos están en las transiciones de fase en lugar de los propios puntos de la constelación. La relación entre el valor del símbolo y la transición se da en la Figura\(\PageIndex{13}\) (d). Por ejemplo, las transiciones mostradas en la Figura\(\PageIndex{14}\) para seis intervalos de tiempo sucesivos describen la secuencia de bits de entrada\(\mathsf{000110110101}\). Su forma de onda y espectro se muestran en la Figura\(\PageIndex{15}\). Más detalle del espectro se muestra en la Figura\(\PageIndex{16}\). En la práctica con filtros realistas y permitiendo las transiciones más largas, la modulación\(π/4\) -DQPSK logra una eficiencia de modulación de\(1.62\text{ bits/s/Hz}\), la misma que\(π/4\) -QPSK, pero por supuesto con mayor resiliencia a los cambios en la ruta de transmisión.

En un esquema diferencial, los datos transmitidos están determinados por

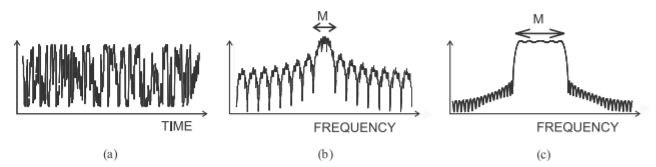
Figura\(\PageIndex{15}\): Detalles de la modulación digital obtenida mediante modulación por desplazamiento de fase diferencial (\(π/4\)- DQPSK): (a) forma de onda moduladora; (b) espectro de la portadora modulada, con\(\mathsf{M}\) denotar el canal principal; y (c) detalles del espectro de la portadora modulada enfocándose en el canal principal.

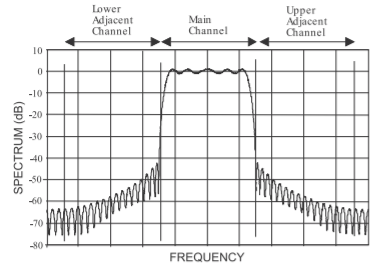
Figura\(\PageIndex{16}\): Espectro detallado de una señal\(π/4\) -DQPSK que muestra el canal principal y los canales adyacentes inferior y superior.

comparar un símbolo con el símbolo recibido previamente, de modo que los datos se determinan a partir del cambio de fase de la portadora en lugar de la fase real de la portadora. Este proceso de inferir los datos realmente enviados desde los símbolos recibidos se llama decodificación. Cuando se introdujo la codificación\(π/4\) -DQPSK a principios de la década de 1990, el DSP disponible para un teléfono móvil acababa de alcanzar la complejidad suficiente. Hoy en día, la codificación se utiliza con todos los sistemas de radio digital y es más sofisticada que solo el esquema diferencial de DQPSK. Hay nuevas formas de manejar la ambigüedad de la fase portadora. La sofisticación de los esquemas de codificación modernos está más allá del alcance del tema centrado en el hardware de este libro.

2.8.6 Desplazamiento Quadra de Desplazamiento de Fase, OQPSK

El esquema de modulación de desplazamiento de fase cuadra offset (OQPSK) evita las transiciones que pasan por el origen en el diagrama de constelación (ver Figura\(\PageIndex{18}\) (a)). Como en todos los esquemas QPSK, hay dos bits por símbolo, pero ahora se usa un bit para modular inmediatamente la señal RF, mientras que el otro bit se retrasa medio periodo de símbolo, como se muestra en la Figura\(\PageIndex{17}\). El cambio de fase máximo para una transición de bits es\(90^{\circ}\), y cuando\(Q_{K}\) se retrasa,\(180^{\circ}\) es posible un cambio de fase total de aproximadamente durante un símbolo. El

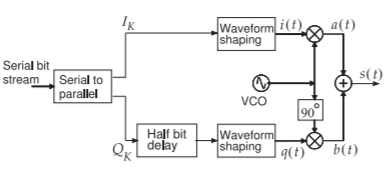
Figura\(\PageIndex{17}\): Diagrama de bloques de un modulador OQPSK.

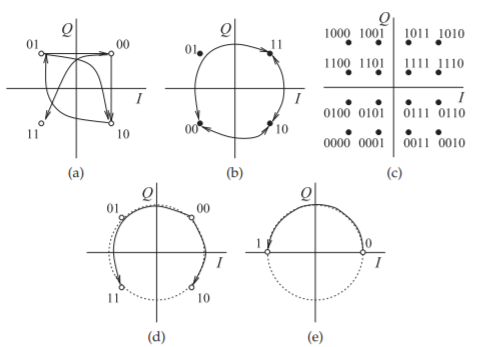
Figura\(\PageIndex{18}\): Diagramas de constelación para diversos formatos de modulación: (a) OQPSK; (b) GMSK; (c) 16-QAM; (d) SOQPSK (también FOQPSK); y (e) SBPSK.

diagrama de constelación se muestra en la Figura\(\PageIndex{18}\) (a).

El modulador OQPSK se puede implementar usando electrónica relativamente simple con un circuito de retardo digital que retrasa el\(Q\) bit a la mitad de un período de símbolo y filtros de paso bajo que dan forma a los\(Q\) bits\(I\) y. El esquema OQPSK también se denomina modulación por desplazamiento de fase en cuadratura escalonada (SQPSK). Se puede obtener un mejor rendimiento mediante el uso de DSP para dar forma a\(Q\) las transiciones\(I\) y para que cambien suavemente y la trayectoria del fasor casi siga un círculo. En consecuencia\(I\) y\(Q\) cambiar juntos, pero de tal manera que el PMEPR se mantenga cerca de\(0\text{ dB}\). Dos técnicas de modulación que implementan esto son los esquemas QPSK (SOQPSK) y Feher QPSK (FQPSK). Los diagramas de constelación para SOQPSK y FQPSK se muestran en la Figura\(\PageIndex{18}\) (d). Estos son esquemas de modulación digital de envolvente constante. Al igual que con OQPSK, el\(Q\) bit se retrasa la mitad de un período de símbolo\(I\) y las señales de\(Q\) banda base están conformadas por un filtro de medio seno. La ventaja es que se pueden usar diseños de amplificadores de saturación de alta eficiencia y prolongar la duración de la batería. Existe un formato de modulación similar llamado modulación por desplazamiento de fase binaria conformada (SBPSK) que, como se esperaba, tiene dos puntos de constelación como se muestra en la Figura\(\PageIndex{18}\) (e). SOQPSK, FQPSK y SBPSK son esquemas de modulación de fase continua (CPM), como la fase

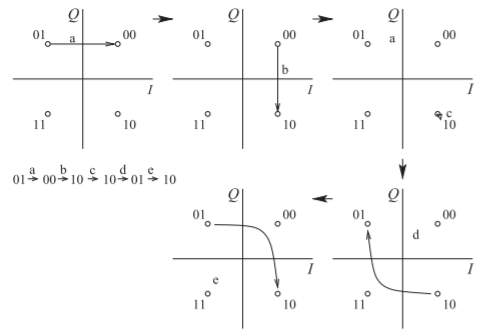
Figura\(\PageIndex{19}\): Diagrama de constelación de modulación OQPSK para la secuencia de bits\(\mathsf{010010100110}\).

nunca cambia abruptamente. En cambio, la fase cambia suavemente, logrando una alta eficiencia de modulación y manteniendo una envolvente constante. La implementación del receptor, sin embargo, es compleja. Los esquemas de CPM tienen buena inmunidad a la interferencia y se usan comúnmente en sistemas militares.

Ejemplo\(\PageIndex{3}\): OQPSK Modulation

Dibuje los diagramas de constelación para la secuencia de bits\(\mathsf{010010100110}\) usando modulación OQPSK.

Solución

La secuencia de bits se separa primero en el flujo paralelo\(\mathsf{01-00-10-10-01-10}\). El\(I\) bit cambia primero, seguido del\(Q\) bit retrasado la mitad del tiempo de un bit. Cinco diagramas de constelación se muestran en la Figura\(\PageIndex{19}\) con las transiciones enviando la secuencia de bits.

2.8.7\(3\pi /8\) -8PSK, Modulación giratoria de desplazamiento de fase de ocho estados

El esquema de modulación\(3π/8\) -8PSK es similar a\(π/4\) -DQPSK en el sentido de que la rotación de la constelación ocurre de un intervalo de tiempo al siguiente. Esta vez, sin embargo, la rotación de la constelación de un símbolo al siguiente es\(3π/8\). Este esquema de modulación se utiliza en las velocidades de datos mejoradas para el sistema de evolución GSM (EDGE), y proporciona tres bits por símbolo (idealmente) en comparación con GMSK utilizado en GSM que tiene dos bits por símbolo (idealmente). Con algunos otros cambios, GSM/EDGE proporciona transmisión de datos de hasta\(128\text{ kbits/s}\), más rápido que\(48\text{ kbits/s}\) lo posible con GSM.

Los esquemas de modulación en cuadratura con cuatro estados, como QPSK, tienen dos\(I\) estados y dos\(Q\) estados que se pueden establecer filtrando paso bajo los\(Q\) flujos de bits\(I\) y. Para esquemas de modulación de orden superior como 8-PSK, este enfoque no funcionará. En su lugar,\(i(t)\) y\(q(t)\) se establecen en la unidad DSP y luego se convierten usando un DAC para generar las señales analógicas aplicadas

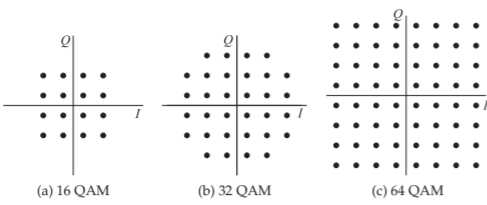
Figura\(\PageIndex{20}\): Diagramas de constelación QAM.

al modulador de hardware. Alternativamente, la señal modulada se crea directamente en el DSP y un DAC la convierte en IF y un mezclador de hardware la convierte en RF. QAM

2.8.8 Resumen

La modulación PSK se implementa en muchos estándares de radio, incluidos todos los estándares celulares después de 2G. Había un sistema 2G que usaba\(π/4\) DQPSK pero que ya no es compatible. Los estándares de radio modernos soportan muchos formatos de modulación pero en situaciones de alta interferencia BPSK, QPSK y 8-PSK tienen el mejor rendimiento. Si bien QPSK fue despedido en 2G y 3G por dificultades con la recuperación de portadora, 4G y 5G tienen otro método para implementar la recuperación de portadora que permite usar QPSK por sí solo. GMSK sigue siendo compatible con los teléfonos celulares modernos pero la infraestructura, es decir, las estaciones base, están empezando a retirarse.

La mayoría de los esquemas de modulación descritos en esta sección se introdujeron como compensaciones óptimas de eficiencia de modulación, resistencia a la interferencia y complejidad del hardware. Algunos, como BPSK, consumen muy poca energía y son adecuados para las aplicaciones de Internet de las cosas (IoT) que deben tener una vida útil de la batería de diez años.

Notas al pie

[1] Este teorema fue descubierto independientemente por varias personas y también es conocido como el teorema de muestreo Nyquist-Shannon, el Nyquist-Shannon-Kotelnikov, el Whittaker-Shannon-Kotelnikov, el Whittaker-Nyquist-Kotelnikov-Shannon (WKS), así como el teorema cardinal de la teoría de la interpolación. El teorema afirma [13]: “Si una función no\(x(t)\) contiene frecuencias superiores a\(B\) hercios, se determina completamente dando sus ordenadas en una serie de puntos separados por\(1/(2B)\) segundos”.