3.6: Arquitecturas modernas de transmisores

Los transmisores modernos maximizan tanto la eficiencia espectral como la eficiencia eléctrica mediante el uso de modulación en cuadratura y la supresión de la portadora en la señal de radio. La eficiencia eléctrica se debe lograr junto con especificaciones estrictas sobre la distorsión permisible, y los diseños deben lograrlo con ajustes manuales mínimos. La discusión en esta sección se centra en las comunicaciones de banda estrecha cuando la portadora de RF modulada puede considerarse como un fasor de RF que varía lentamente. Las radios modernas deben implementar diversos esquemas de modulación de orden y también deben implementar métodos de modulación heredados.

3.6.1 Modulador en cuadratura

La mayoría de los esquemas de modulación digital establecen la amplitud y la fase de una portadora. La única excepción es la modulación por desplazamiento de frecuencia (FSK), que cambia la frecuencia de la portadora y tiene mucho en común con FM.

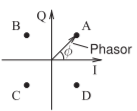
Figura\(\PageIndex{1}\): Diagrama fasor con cuatro estados de fase discretos que se pueden establecer mediante combinación\(I\) y\(Q\) señales.

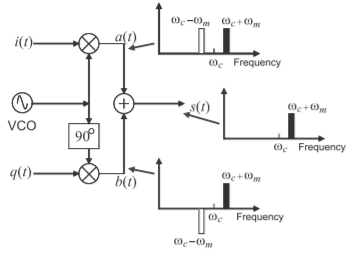
Figura\(\PageIndex{2}\): Modulador en cuadratura que muestra espectros intermedios.

Entonces, en la mayoría de los esquemas de modulación digital, establecer la amplitud y fase de una portadora aborda un punto en un diagrama fasor. En la Figura se muestra un diagrama de fasores con cuatro estados discretos\(\PageIndex{1}\). El circuito que implementa esta modulación digital se muestra en la Figura 3.4.6.

3.6.2 Modulación en cuadratura

La modulación en cuadratura describe el proceso de conversión de frecuencia en el que las partes real e imaginaria del fasor RF se varían por separado. Un subsistema que implementa la modulación en cuadratura se muestra en la Figura\(\PageIndex{2}\). Este es un circuito bastante ingenioso. El funcionamiento de este subsistema se describe por lo que se conoce como la ecuación de modulación en cuadratura generalizada:

\[\label{eq:1}s(t)=i(t)\cos[\omega_{c}t+\varphi_{i}(t)]+q(t)\sin[\omega_{c}t+\varphi_{q}(t)] \]

donde,\(i(t)\) y\(q(t)\) encarnan la regla de modulación particular para la amplitud,\(\varphi_{i}(t)\) y\(\varphi_{q}(t)\) encarnan la regla de modulación particular para la fase, y\(\omega_{c}\) es la frecuencia del radián portador. En términos de las señales identificadas en la Figura\(\PageIndex{2}\), la ecuación de modulación en cuadratura puede escribirse como

\[\begin{align}\label{eq:2}s(t)&=a(t)+b(t) \\ \label{eq:3}a(t)&=i(t)\cos[\omega_{c}t+\varphi_{i}(t)] \\ \label{eq:4}b(t)&=q(t)\sin[\omega_{c}t+\varphi_{q}(t)]\end{align} \]

La figura\(\PageIndex{2}\) muestra que ambas\(a(t)\) y\(b(t)\) tienen dos bandas, una por encima y otra por debajo de la frecuencia de la portadora,\(\omega_{c}\). Sin embargo, hay una diferencia. El LO (designado aquí como el VCO) se desplaza\(90^{\circ}\) (quizás usando una línea de retardo RC) de modo que los componentes de frecuencia de\(b(t)\) tienen una relación de fase diferente a la portadora que los de\(a(t)\). Cuando\(a(t)\) y\(b(t)\) se combinan, el contenido del portador se cancela, al igual que una de las bandas laterales siempre que\(q(t)\) sea una versión de\(90^{\circ}\) fase desplazada de\(i(t)\). Esto es exactamente lo que se desea: el portador no debe ser transmitido, ya que no contiene información. Además, es deseable transmitir solo una banda lateral, ya que contiene toda la información en la señal moduladora. Este tipo de modulación es la modulación SSB-SC. En la siguiente sección, se utiliza la modulación de frecuencia para demostrar el funcionamiento de SSB-SC.

3.6.3 Modulación de frecuencia

La modulación de frecuencia se considera aquí para demostrar el funcionamiento de SSB-SC. Dejar\(i(t)\) y\(q(t)\) ser señales de ancho de banda finito centradas en frecuencia radián\(\omega_{m}\) con sus fases\(\varphi_{i}(t)\) y\(\varphi_{q}(t)\) elegidas de manera que\((\varphi_{q}(t) −\varphi_{i}(t))\) sea\(90^{\circ}\) en promedio. Esto se muestra en la Figura\(\PageIndex{2}\), donde\(\omega_{m}\) representa los componentes de frecuencia de\(i(t)\) y\(q(t)\). Con referencia a la Figura\(\PageIndex{2}\),

\[\label{eq:5}i(t)=\cos(\omega_{m}t)\quad\text{and}\quad q(t)=-\sin(\omega_{m}t) \]

y la ecuación general de modulación en cuadratura, Ecuación\(\eqref{eq:1}\), se convierte

\[\label{eq:6}s(t)=i(t)\cos(\omega_{c}t)+q(t)\sin(\omega_{c}t)=a(t)+b(t) \]

donde

\[\label{eq:7}a(t)=\frac{1}{2}\{\cos[(\omega_{c}-\omega_{m})t]+\cos[(\omega_{c}+\omega_{m})t]\} \]

y

\[\label{eq:8}b(t)=\frac{1}{2}\{\cos[(\omega_{c}+\omega_{m})t]-\cos[(\omega_{c}-\omega_{m})t]\} \]

Así, la señal modulada en frecuencia combinada en la salida es

\[\label{eq:9}s(t)=a(t)+b(t)=\cos[(\omega_{c}+\omega_{m})t] \]

y tanto el portador como la banda lateral inferior están suprimidos. La banda lateral inferior,\(\cos[(\omega_{c}−\omega_{m})t]\), también se conoce como la imagen que puede no ser exactamente cero debido a las imperfecciones del circuito. En los moduladores es importante suprimir esta imagen, y en los demoduladores es importante que las señales no deseadas a la frecuencia de imagen no se conviertan junto con las señales deseadas.

3.6.4 Modulación polar

En la modulación polar, las señales\(i(t)\) y\(q(t)\) cuadratura se convierten en forma polar como\(\phi (t)\) componentes de amplitud\(A(t)\) y fase. Esto se hace en la unidad DSP o, si una portadora de RF modulada es todo lo que se proporciona, utilizando un detector de envolvente para extraer\(A(t)\) y un limitador para extraer la información de fase correspondiente\(\phi (t)\). Dos arquitecturas de moduladores polares se muestran en la Figura 3.7.1. En la primera arquitectura, Figura 3.7.1 (a),\(A(t)\) y\(\phi (t)\) están disponibles y\(A(t)\) se utilizan para modular en amplitud la portadora de RF, que luego es amplificada por un amplificador de potencia (PA). La señal de fase,\(\phi (t)\), es la entrada a un modulador de fase implementado como un PLL. La salida del PLL se alimenta a un amplificador eficiente que opera cerca de la saturación (también llamado amplificador de saturación). Las salidas de los dos amplificadores se combinan para obtener la gran señal de RF modulada a transmitir.

En la segunda arquitectura de modulación polar, Figura 3.7.1 (b), una señal de RF modulada de baja potencia se descompone en sus componentes de amplitud y fasemodulación. El componente de fase,\(\phi (t)\), se extrae utilizando un limitador que produce una forma de onda similar a un pulso con los mismos cruces por cero que la señal de RF modulada. Así se captura la fase de la señal de RF. Esto se alimenta entonces a un amplificador de saturación cuya ganancia es controlada por la envolvente portadora, o\(A(t)\). Específicamente,\(A(t)\) se extrae mediante un detector de envolvente, siendo una implementación sencilla un rectificador seguido de un filtro de paso bajo con una frecuencia de esquina igual al ancho de banda de la modulación. \(A(t)\)luego impulsa una fuente de alimentación conmutada (y por lo tanto eficiente) que impulsa el amplificador de potencia de saturación.