1.6: Ondas electromagnéticas
- Page ID
- 81850
Ecuaciones de Maxwell
En este texto,\(V\) y\(I\) denotan voltaje de CC y corriente respectivamente mientras\(v\) y\(i\) denotan CA o voltaje variable en el tiempo y corriente. En el análisis de circuitos, no nos preocupa lo que sucede fuera de estos cables. Solo nos interesan los voltajes de nodo y las corrientes a través de cables. Además, los voltajes y corrientes en el circuito se describen como funciones de tiempo\(t\) pero no de posición\((x, y, z)\). También se supone que los dispositivos como resistencias, condensadores e inductores son puntuales y no se extienden con respecto a la posición\((x, y, z)\). Este conjunto de suposiciones es solo un modelo. En realidad, si dos nodos en un circuito tienen una diferencia de voltaje entre ellos, entonces necesariamente se ejerce una fuerza sobre cargas cercanas no en la trayectoria del circuito. Esta fuerza por unidad de carga es la intensidad del campo eléctrico\(\overrightarrow{E}\). De manera similar, si hay corriente que fluye a través de un cable, necesariamente hay una fuerza ejercida sobre los electrones en los bucles cercanos de alambre, y esta fuerza por elemento de corriente unitaria es la densidad de flujo magnético\(\overrightarrow{B}\). La energía se puede almacenar en un campo eléctrico o magnético. En capítulos posteriores, discutiremos dispositivos, incluyendo antenas, dispositivos electroópticos, dispositivos fotovoltaicos, lámparas y láseres, que convierten la energía de un campo electromagnético hacia o desde la electricidad. Se utilizan cuatro cantidades vectoriales interrelacionadas para describir los campos electromagnéticos. Estos campos vectoriales son funciones de posición\((x, y, z)\) y tiempo\(t\). Los cuatro campos vectoriales son
- \(\overrightarrow{E}(x, y, z, t) =\)Intensidad del campo eléctrico en\(\frac{V}{m}\)
- \(\overrightarrow{D}(x, y, z, t) =\)Densidad de campo de desplazamiento en\(\frac{C}{m^2}\)
- \(\overrightarrow{H}(x, y, z, t) =\)Intensidad de campo magnético en\(\frac{A}{m}\)
- \(\overrightarrow{B}(x, y, z, t) =\)Densidad de flujo magnético en\(\frac{Wb}{m^2}\)
En estas expresiones,\(V\) representa las unidades voltios,\(C\) representa las unidades culombios,\(A\) representa las unidades amperios, y\(Wb\) representa las unidades webers. Las abreviaturas adicionales para las unidades se enumeran en el Apéndice B.
Ley de Coulomb:
\[\overrightarrow{F} = \frac{Q_1 Q_2 \hat a_r}{4 \pi \epsilon r^{2}} \nonumber \]
nos dice que los objetos cargados ejercen fuerzas sobre otros objetos cargados. En esta expresión,\(Q_1\) y\(Q_2\) están la magnitud de las cargas en culombios. La cantidad\(\epsilon\) es la permitividad del material circundante en unidades faradios por metro, y se discute más a fondo en 1.6.3 y 2.1.3. La cantidad\(r\) es la distancia entre las cargas en metros, y\(\hat a_r\) es un vector unitario que apunta a lo largo de la dirección entre las cargas. La fuerza en newtons está representada por\(\overrightarrow{F}\). Los cargos opuestos atraen, y los cargos similares repelen. La intensidad del campo eléctrico es la fuerza por unidad de carga, por lo que la intensidad del campo eléctrico debida a una carga puntual viene dada por\[\overrightarrow{E} = \frac{Q \hat a_r}{4 \pi \epsilon r^{2}} \nonumber \]
Estos campos vectoriales pueden describir fuerzas sobre cargas o corrientes en un circuito así como fuera de la trayectoria de un circuito. Las ecuaciones de Maxwell relacionan campos eléctricos y magnéticos variables en el tiempo. Las ecuaciones de Maxwell en forma diferencial son:
\[\overrightarrow{\nabla} \times \overrightarrow{E} = -\frac{\partial \overrightarrow{B}}{\partial t} \quad \text{Faraday's Law} \nonumber \]
\[\overrightarrow{\nabla} \times \overrightarrow{H} = \overrightarrow{J} + \frac{\partial \overrightarrow{D}}{\partial t} \quad \text{Ampere's Law} \nonumber \]
\[\overrightarrow{\nabla} \cdot \overrightarrow{D} = \rho_{ch} \quad \text{Gauss's Law for the Electric Field} \nonumber \]
\[\overrightarrow{\nabla} \cdot \overrightarrow{B} = 0 \quad \text{Gauss's Law for the Magnetic Field} \nonumber \]
Las cantidades adicionales en las ecuaciones de Maxwell son la densidad de corriente volumétrica\(\overrightarrow{J}\) en\(\frac{A}{m^2}\) y la densidad de carga\(\rho_{ch}\) en\(\frac{C}{m^3}\). En este texto, no estaremos resolviendo las ecuaciones de Maxwell, pero encontraremos referencias a ellas.
La cantidad\(\overrightarrow{\nabla}\) se llama del operador. En coordenadas cartesianas, viene dada por
\[\overrightarrow{\nabla} =\hat a_x \frac{\partial}{\partial x} + \hat a_y \frac{\partial}{\partial y} + \hat a_z \frac{\partial}{\partial z}. \nonumber \]
Cuando este operador actúa sobre una función escalar,\(\overrightarrow{\nabla}f\), se llama el gradiente. El gradiente de una función escalar devuelve un vector que representa la derivada espacial de la función, y apunta en la dirección del mayor cambio en esa función. En las ecuaciones de Maxwell,\(\overrightarrow{\nabla}\) actúa sobre funciones vectoriales, en lugar de escalar. A la operación\(\overrightarrow{\nabla} \times \overrightarrow{E}\) se le llama rizo, y a la operación\(\overrightarrow{\nabla} \cdot \overrightarrow{E}\) se le llama divergencia. Ambas operaciones representan tipos de derivadas espaciales de funciones vectoriales. El operador del obedece la identidad
\[\nabla^2 =\overrightarrow{\nabla} \cdot \overrightarrow{\nabla}. \nonumber \]
La operación\(\nabla^2f\) se llama Laplaciana de una función escalar, y representa la segunda derivada espacial de esa función.
Ondas electromagnéticas en el espacio libre
Las ondas electromagnéticas viajan a través del espacio vacío a la velocidad de la luz en el espacio libre\(c = 2.998 \cdot 10^8 \frac{m}{s}\),, y a través de otros materiales a velocidades inferiores a\(c\). Para una onda electromagnética sinusoidal, la velocidad de propagación es el producto de la frecuencia y la longitud de onda\[|\overrightarrow{v}| =f \lambda \nonumber \]
donde\(|\overrightarrow{v}|\) es la magnitud de la velocidad en\(\frac{m}{s}\),\(f\) es la frecuencia en Hz, y\(\lambda\) es la longitud de onda en metros. En el espacio libre, esto se convierte en\[c =f \lambda. \nonumber \]
La velocidad de la luz en el espacio libre está relacionada con dos constantes que describen el espacio libre. \[c = \frac{1}{\sqrt{\epsilon_0\mu_0}} \nonumber \]
La permitividad del espacio libre viene dada por\(\epsilon_0 = 8.854 \cdot 10^{-12} \frac{F}{m}\) donde\(F\) representa faradios, y la permeabilidad del espacio libre viene dada por\(\mu_0 = 1.257 \cdot 10^{-6} \frac{H}{m}\) donde\(H\) representa henries. (Las constantes especificadas en esta sección y en el Apéndice A se redondean a cuatro dígitos significativos).
En el espacio libre, la intensidad del campo eléctrico\(\overrightarrow{E}\) y la densidad de flujo de desplazamiento\(\overrightarrow{D}\) están relacionadas por\(\epsilon_0\). \[\overrightarrow{D} = \mu_0 \overrightarrow{E} \nonumber \]
Relacionadamente en el espacio libre, la intensidad del campo magnético\(\overrightarrow{H}\) y la densidad de flujo magnético\(\overrightarrow{B}\) están relacionadas por\(mu_0\). \[\overrightarrow{B} = \mu_0 \overrightarrow{H}. \nonumber \]
Ondas Electromagnéticas en Materiales
Los campos electromagnéticos interactúan de manera muy diferente con conductores y con aisladores. Los campos electromagnéticos no se propagan en conductores perfectos. En cambio, las cargas y corrientes se acumulan en la superficie. Si bien ningún material es un conductor perfecto, los metales comúnmente encontrados como el cobre y el aluminio son muy buenos conductores. Cuando estos materiales se colocan en un campo electromagnético externo, las cargas superficiales y las corrientes se acumulan, y el campo electromagnético en el material se acerca rápidamente a cero. Los campos electromagnéticos se propagan a través de aisladores perfectos para largas distancias sin decaer, y no se pueden acumular cargas o corrientes en la superficie porque no hay electrones libres de sus átomos. En los dieléctricos prácticos, las ondas electromagnéticas se propagan largas distancias con muy poca atenuación. Por ejemplo, las ondas electromagnéticas ópticas permanecen lo suficientemente fuertes como para detectarse después de propagarse cientos de kilómetros a través de fibras ópticas hechas de dióxido de silicio puro [10, p. 886].
Resistencia\(R\) en ohmios, capacitancia\(C\) en faradios e inductancia\(L\) en henries describen las propiedades eléctricas de los dispositivos. La resistividad\(\rho\) en\(\Omega m\), la permitividad\(\epsilon\) en\(\frac {F}{m}\) y la permeabilidad\(\mu\) en\(\frac{H}{m}\) describen las propiedades eléctricas de los materiales. Las cantidades\(\rho\)\(\epsilon\), y\(\mu\) describir las propiedades de los materiales solo mientras que las cantidades\(R\)\(C\), e\(L\) incorporar efectos el material, la forma y el tamaño de un dispositivo.
La resistividad\(\rho\) es una medida de la incapacidad de las cargas u ondas electromagnéticas para propagarse a través de un material. Los conductores tienen una resistividad muy pequeña mientras que los aislantes tienen una gran resistividad. A veces se utiliza conductividad eléctrica\(\frac{1}{\Omega m}\),\(\sigma =\frac{1}{\rho}\) en unidades, en lugar de la resistividad. Para un dispositivo hecho de un material uniforme con longitud\(l\) y área de sección transversal\(A\), la resistencia y resistividad están relacionadas por\[R =\frac{\rho l}{A}. \nonumber \]
La resistencia es una medida de la incapacidad de las cargas u ondas electromagnéticas para fluir a través de un dispositivo, mientras que la resistividad es una medida de la incapacidad de fluir a través de un material.
\(\mu\)La permeabilidad es una medida de la capacidad de un material para almacenar energía en el campo magnético debido a las corrientes distribuidas por todo el material. Los materiales también pueden describirse por su permeabilidad relativa\(\mu_r\), una medida sin unidades. \[\mu_r = \frac{\mu}{\mu_0} \nonumber \]
Mientras que la permeabilidad describe un material, la inductancia describe un dispositivo. La densidad de flujo magnético en un material es una versión escalada de la intensidad del campo magnético.
\[\overrightarrow{B} =\mu\overrightarrow{H} \nonumber \]
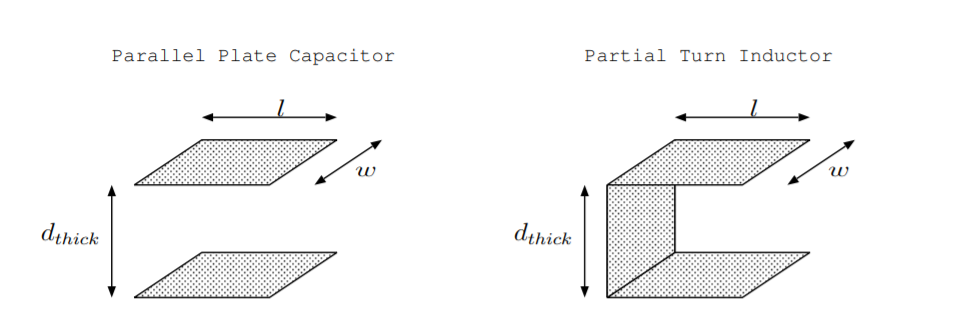
A menudo, los aislantes tienen permeabilidades cercanas,\(mu_0\) mientras que los conductores utilizados para hacer imanes permanentes tienen permeabilidades significativamente mayores. La parte derecha de la Figura\(\PageIndex{1}\): muestra una bobina de giro parcial en vacío con longitud\(l\)\(d_{thick}\), grosor y ancho\(w\). La inductancia y permeabilidad de este dispositivo están relacionadas por [11, p. 311]
\[L =\frac{\mu d_{thick} l}{w}. \nonumber \]
La permitividad\(\epsilon\) es una medida de la capacidad de un material para almacenar energía como un campo eléctrico debido a la separación de carga distribuida por todo el material. Los materiales también pueden describirse por su permitividad relativa\(\epsilon_r\), una medida sin unidades. \[\epsilon_r =\frac{\epsilon}{\epsilon_0} \nonumber \]
La densidad de flujo de desplazamiento en un material es una versión a escala de la intensidad del campo eléctrico. \[\overrightarrow{D} =\epsilon\overrightarrow{E} \nonumber \]
Algunos aislantes tienen una permitividad cientos de veces mayor que la permitividad del espacio libre. La permitividad es una medida de la capacidad de almacenar energía en un material, mientras que la capacitancia es una medida de la capacidad de almacenar energía en un dispositivo.
En la parte izquierda de la Figura se muestra un condensador de placa paralela uniforme con área de sección transversal de placas\(A =l \cdot w\) y distancia entre placas\(d_{thick}\)\(\PageIndex{1}\), y tiene capacitancia\[C =\frac{\epsilon A}{d_{thick}} \nonumber \] donde\(\epsilon\) está la permitividad del aislador entre las placas.
La permitividad, permeabilidad y resistividad dependen de la frecuencia. En algunos contextos, se puede ignorar la dependencia de la frecuencia, y a lo largo de la mayor parte de este texto, se asumirá que estas cantidades son constantes. En otros contextos, la dependencia de la frecuencia puede ser bastante significativa. Por ejemplo, la permitividad de los materiales semiconductores es una función fuerte de la frecuencia para frecuencias cercanas a la brecha de energía del semiconductor. La permitividad\(\epsilon(\omega)\) y resistividad no\(\rho(\omega)\) son independientes. Si uno de ellos es conocido como una función de la frecuencia y\(\mu\) se asume constante, el otro se puede derivar. Esta relación se conoce como la relación Kramers Kronig [10] u ocasionalmente como la fórmula de dispersión dieléctrica [15].
Cuando se discuten las propiedades eléctricas de un dispositivo, la resistencia, la inductancia y la capacitancia se combinan en una medida compleja, la impedancia. De igual manera, algunos autores consideran conveniente combinar resistividad, permitividad y permeabilidad en un par de medidas complejas de las propiedades eléctricas de los materiales [6]. Se define\(\epsilon^* =\epsilon+j\rho\) la permitividad compleja y se define la permeabilidad compleja\(\mu^* =\mu+j\rho_{mag}\). La cantidad\(\rho\) representa la resistividad que es una medida de la energía convertida en calor a medida que una carga fluye a través de un material debido a un campo eléctrico aplicado. La cantidad\(\rho_{mag}\) representa una medida análoga de energía convertida en calor a partir de corrientes en un campo magnético aplicado. En este texto no se utilizarán permitividad y permeabilidad complejas.