16.7: Teorema de Stokes

Objetivos de aprendizaje

• Explicar el significado del teorema de Stokes.
• Utilice el teorema de Stokes para evaluar una integral de línea.
• Utilice el teorema de Stokes para calcular una integral de superficie.
• Usa el teorema de Stokes para calcular un rizo.

En esta sección, estudiamos el teorema de Stokes, una generalización dimensional superior del teorema de Green. Este teorema, al igual que el Teorema Fundamental para Integrales de Línea y Teorema de Verde, es una generalización del Teorema Fundamental del Cálculo a dimensiones superiores. El teorema de Stokes relaciona una superficie vectorial integral sobre la superficie\(S\) en el espacio con una línea integral alrededor del límite de\(S\). Por lo tanto, al igual que los teoremas anteriores a él, el teorema de Stokes se puede utilizar para reducir una integral sobre un objeto geométrico\(S\) a una integral sobre el límite de\(S\). Además de permitirnos traducir entre integrales de línea e integrales superficiales, el teorema de Stokes conecta los conceptos de curl y circulación. Además, el teorema tiene aplicaciones en mecánica de fluidos y electromagnetismo. Utilizamos el teorema de Stokes para derivar la ley de Faraday, un resultado importante que involucra campos eléctricos.

Teorema de Stokes

El teorema de Stokes dice que podemos calcular el flujo de\( curl \,\vecs{F}\) a través de la superficie\(S\) conociendo información solo sobre los valores de\(\vecs{F}\) a lo largo del límite de\(S\). Por el contrario, podemos calcular la integral de línea del campo vectorial\(\vecs{F}\) a lo largo del límite de la superficie\(S\) al traducirla a una doble integral del rizo de\(\vecs{F}\) más\(S\).

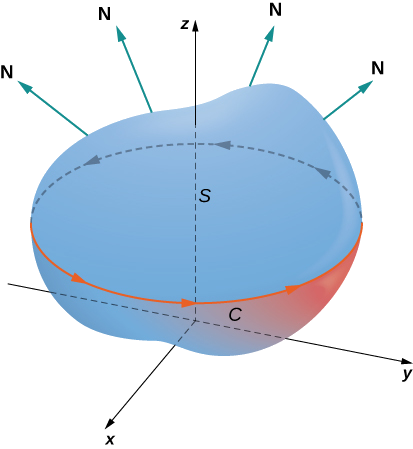
Dejar\(S\) ser una superficie lisa orientada con vector normal de unidad\(\vecs{N}\). Además, supongamos que el límite de\(S\) es una simple curva cerrada\(C\). La orientación de\(S\) induce la orientación positiva de\(C\) si, al caminar en la dirección positiva alrededor\(C\) con la cabeza apuntando en la dirección de\(\vecs{N}\), la superficie siempre está a su izquierda. Con esta definición en su lugar, podemos exponer el teorema de Stokes.

Teorema\(\PageIndex{1}\): Stokes’ Theorem

Dejar\(S\) ser una superficie orientada lisa por tramos con un límite que es una simple curva cerrada\(C\) con orientación positiva (Figura\(\PageIndex{1}\)). Si\(\vecs{F}\) es un campo vectorial con funciones componentes que tienen derivadas parciales continuas en una región abierta que contiene\(S\), entonces

\[\int_C \vecs{F} \cdot d \vecs{r} = \iint_S curl \, \vecs{F} \cdot d\vecs S. \label{Stokes1} \]

Figura\(\PageIndex{1}\): El teorema de Stokes relaciona la integral de flujo sobre la superficie con una línea integral alrededor del límite de la superficie. Tenga en cuenta que la orientación de la curva es positiva.

Supongamos que la superficie\(S\) es una región plana en el\(xy\) plano -con orientación hacia arriba. Entonces el vector normal de la unidad es\(\vecs{k}\) y la superficie integral

\[\iint_S curl \, \vecs{F} \cdot d\vecs{S} \nonumber \]

es en realidad la doble integral

\[\iint_S curl \, \vecs{F} \cdot \vecs{k} \, dA. \nonumber \]

En este caso especial, el teorema de Stokes da

\[\int_C \vecs{F} \cdot d\vecs{r} = \iint_S curl \, \vecs{F} \cdot \vecs{k} \, dA. \nonumber \]

Sin embargo, esta es la forma de flujo del teorema de Green, que nos muestra que el teorema de Green es un caso especial del teorema de Stokes. El teorema de Green solo puede manejar superficies en un plano, pero el teorema de Stokes puede manejar superficies en un plano o en el espacio.

La prueba completa del teorema de Stokes está fuera del alcance de este texto. Miramos una explicación intuitiva de la verdad del teorema y luego vemos la prueba del teorema en el caso especial de que la superficie\(S\) es una porción de una gráfica de una función, y\(S\), el límite de\(S\), y\(\vecs{F}\) son todos bastante mansos.

Prueba

Primero, nos fijamos en una prueba informal del teorema. Esta prueba no es rigurosa, sino que pretende dar una sensación general de por qué el teorema es cierto. Dejar\(S\) ser una superficie y dejar\(D\) ser un pequeño trozo de la superficie para que\(D\) no comparta ningún punto con el límite de\(S\). Elegimos\(D\) ser lo suficientemente pequeños para que pueda aproximarse por un cuadrado orientado\(E\). Dejar\(D\) heredar su orientación de\(S\), y dar\(E\) la misma orientación. Este cuadrado tiene cuatro lados; denotarlos\(E_l, \, E_r, \, E_u\), y\(E_d\) para los lados izquierdo, derecho, arriba y abajo, respectivamente. En el cuadrado, podemos usar la forma de flujo del teorema de Green:

\[\int_{E_l+E_d+E_r+E_u} \vecs{F} \cdot d \vecs{r} = \iint_E curl \, \vecs{F} \cdot \vecs{N} \, d \vecs{S} = \iint_E curl \, \vecs{F} \cdot d\vecs{S}. \nonumber \]

Para aproximar el flujo sobre toda la superficie, agregamos los valores del flujo en los cuadrados pequeños aproximándose a pequeños trozos de la superficie (Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): Picar la superficie en trozos pequeños. Las piezas deben ser lo suficientemente pequeñas como para que puedan aproximarse por un cuadrado.

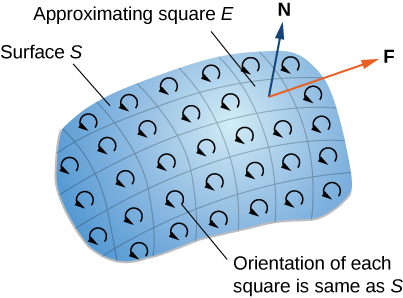
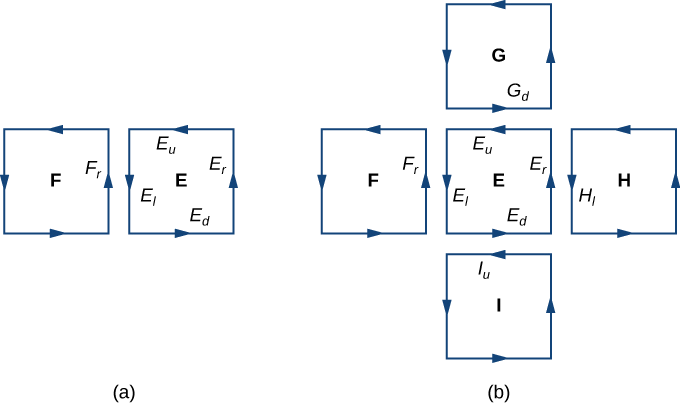
Según el teorema de Green, el flujo a través de cada cuadrado aproximado es una línea integral sobre su límite. Dejar\(F\) ser un cuadrado aproximado con una orientación heredada de\(S\) y con un lado derecho\(E_l\) (así\(F\) es a la izquierda de\(E\)). Vamos a\(F_r\) denotar el lado derecho de\(F\); entonces,\(E_l = - F_r\). En otras palabras, el lado derecho de\(F\) es la misma curva que el lado izquierdo de\(E\), simplemente orientado en la dirección opuesta. Por lo tanto,

\[\int_{E_l} \vecs F \cdot d\vecs r = - \int_{F_r} \vecs F \cdot d\vecs r. \nonumber \]

A medida que sumamos todos los flujos sobre todos los cuadrados aproximándose a la superficie\(S\), integrales de línea

\[\int_{E_l} \vecs{F} \cdot d \vecs{r} \nonumber \]

y

\[ \int_{F_r} \vecs{F} \cdot d\vecs{r} \nonumber \]

se cancelan entre sí. Lo mismo ocurre con las integrales de línea sobre los otros tres lados de\(E\). Estas tres integrales de línea se cancelan con la integral de línea del lado inferior del cuadrado arriba\(E\), la integral de línea sobre el lado izquierdo del cuadrado a la derecha de\(E\), y la línea integral sobre el lado superior del cuadrado de abajo\(E\) (Figura\(\PageIndex{3}\)). Después de que toda esta cancelación ocurre sobre todos los cuadrados aproximados, las únicas integrales de línea que sobreviven son las integrales de línea sobre lados que se aproximan al límite de\(S\). Por lo tanto, la suma de todos los flujos (que, por el teorema de Green, es la suma de todas las integrales de línea alrededor de los límites de los cuadrados aproximados) puede aproximarse por una línea integral sobre el límite de\(S\). En el límite, a medida que las áreas de los cuadrados aproximados van a cero, esta aproximación se acerca arbitrariamente al flujo.

Figura\(\PageIndex{3}\): (a) La línea integral a lo largo\(E_l\) cancela la línea integral a lo largo\(F_r\) porque\(E_l = - F_r\). (b) La línea integral a lo largo de cualquiera de los lados de\(E\) cancela con la línea integral a lo largo de un lado de un cuadrado aproximado adyacente.

Veamos ahora una rigurosa prueba del teorema en el caso especial que\(S\) es la gráfica de la función\(z = f(x,y)\), donde\(x\) y\(y\) variar sobre una región delimitada, simplemente conectada\(D\) de área finita (Figura\(\PageIndex{4}\)). Además, supongamos que\(f\) tiene derivadas parciales continuas de segundo orden. Dejar\(C\) denotar el límite de\(S\) y dejar\(C'\) denotar el límite de\(D\). Entonces,\(D\) es la “sombra” de\(S\) en el plano y\(C'\) es la “sombra” de\(C\). Supongamos que\(S\) está orientado hacia arriba. La orientación en sentido antihorario de\(C\) es positiva, al igual que la orientación antihoraria de\(C'\). Let\(\vecs F(x,y,z) = \langle P,Q,R \rangle\) Ser un campo vectorial con funciones componentes que tienen derivadas parciales continuas.

Figura\(\PageIndex{4}\):\(D\) es la “sombra”, o proyección, de\(S\) en el plano y\(C'\) es la proyección de\(C\).

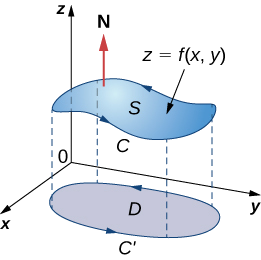
Tomamos la parametrización estándar de\(S \, : \, x = x, \, y = y, \, z = g(x,y)\). Los vectores tangentes son\(\vecs t_x = \langle 1,0,g_x \rangle\) y\(\vecs t_y = \langle 0,1,g_y \rangle\), y por lo tanto\(\vecs t_x \times \vecs t_y = \langle -g_x, \, -g_y, \, 1 \rangle\).

\[\iint_S curl \, \vecs{F} \cdot d\vecs{S} = \iint_D [- (R_y - Q_z)z_x - (P_z - R_x)z_y + (Q_x - P_y)] \, dA, \nonumber \]

donde todas las derivadas parciales son evaluadas\((x,y,g(x,y))\), haciendo que el integrando dependa de\(x\) y\(y\) solo. Supongamos que\(\langle x (t), \, y(t) \rangle, \, a \leq t \leq b\) es una parametrización de\(C'\). Entonces, una parametrización de\(C\) es\(\langle x (t), \, y(t), \, g(x(t), \, y(t))\rangle, \, a \leq t \leq b\). Armados con estas parametrizaciones, la regla de la Cadena, y el teorema de Green, y teniendo en cuenta que\(P\),\(Q\) y\(R\) son todas funciones de\(x\) y\(y\), podemos evaluar la integral de línea

\[ \begin{align*} \int_C \vecs{F} \cdot d \vecs{r} &= \int_a^b (Px'(t) + Qy'(t) + Rz'(t)) \, dt \\[4pt] &= \int_a^b \left[Px'(t) + Qy'(t) + R\left(\dfrac{\partial z}{\partial x} \dfrac{dx}{dt} + \dfrac{\partial z}{\partial y} \dfrac{dy}{dt}\right) \right] dt \\[4pt] &= \int_a^b \left[ \left(P + R \dfrac{\partial z}{\partial x} \right) x' (t) + \left(Q + R \dfrac{\partial z}{\partial y} \right) y'(t) \right] dt \\[4pt] &= \int_{C'} \left(P + R \dfrac{\partial z}{\partial x} \right)\, dx + \left(Q + R \dfrac{\partial z}{\partial y} \right) \, dy \\[4pt] &= \iint_D \left[ \dfrac{\partial}{\partial x} \left( Q + R \dfrac{\partial z}{\partial y} \right) - \dfrac{\partial}{\partial y} \left(P + R \dfrac{\partial z}{\partial x} \right) \right] \, dA \\[4pt] &=\iint_D \left(\dfrac{\partial Q}{\partial x} + \dfrac{\partial Q}{\partial z} \dfrac{\partial z}{\partial x} + \dfrac{\partial R}{\partial x} \dfrac{\partial z}{\partial y} + \dfrac{\partial R}{\partial z}\dfrac{\partial z}{\partial x} \dfrac{\partial z}{\partial y} + R \dfrac{\partial^2 z}{\partial x \partial y} \right) - \left(\dfrac{\partial P}{\partial y} + \dfrac{\partial P}{\partial z} \dfrac{\partial z}{\partial y} + \dfrac{\partial R}{\partial z} \dfrac{\partial z}{\partial y} \dfrac{\partial z}{\partial x} + R \dfrac{\partial^2 z}{\partial y \partial x} \right) \end{align*} \nonumber \]

Por el teorema de Clairaut,

\[\dfrac{\partial^2 z}{\partial x \partial y} = \dfrac{\partial^2 z}{\partial y \partial x} \nonumber \]

Por lo tanto, cuatro de los términos desaparecen de esta doble integral, y nos quedamos con

\[\iint_D [- (R_y - Q_z)Z_x - (P_z - R_x) z_y + (Q_x - P_y)] \, dA, \nonumber \]

que es igual

\[\iint_S curl \, \vecs{F} \cdot d\vecs{S}. \nonumber \]

\(\Box\)

Hemos demostrado que el teorema de Stokes es cierto en el caso de una función con un dominio que es una región simplemente conectada de área finita. Podemos confirmar rápidamente este teorema para otro caso importante: cuando el campo vectorial\(\vecs{F}\) es un campo conservador. Si\(\vecs{F}\) es conservador, el rizo de\(\vecs{F}\) es cero, entonces

\[\iint_S curl \, \vecs{F} \cdot d\vecs{S} = 0. \nonumber \]

Dado que el límite de\(S\) es una curva cerrada, la integral

\[\int_C \vecs{F} \cdot d\vecs{r}. \nonumber \]

también es cero.

Ejemplo\(\PageIndex{1}\): Verifying Stokes’ Theorem for a Specific Case

Verificar que el teorema de Stokes es verdadero para el campo vectorial\(\vecs{F}(x,y) = \langle -z,x,0 \rangle\) y la superficie\(S\), donde\(S\) está el hemisferio, orientado hacia afuera, con parametrización\(\vecs r(\phi, \theta) = \langle \sin \phi \, \cos \theta, \, \sin \phi \, \sin \theta, \, \cos \phi \rangle, \, 0 \leq \theta \leq \pi, \, 0 \leq \phi \leq \pi\) como se muestra en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Verificación del teorema de Stokes para un hemisferio en un campo vectorial.

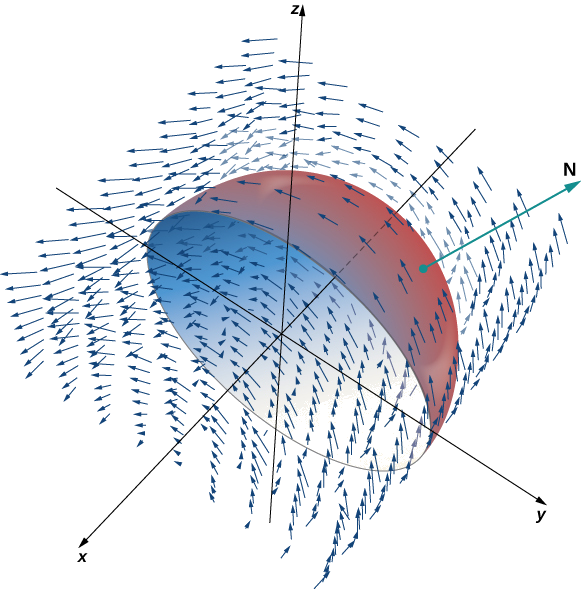
Solución

\(C\)Sea el límite de\(S\). Tenga en cuenta que\(C\) es un círculo de radio 1, centrado en el origen, sentado en plano\(y = 0\). Este círculo tiene parametrización\(\langle \cos t, \, 0, \, \sin t \rangle, \, 0 \leq t \leq 2\pi\). la ecuación para integrales de superficie escalar

\[ \begin{align*} \int_C \vecs{F} \cdot d \vecs{r} &= \int_0^{2\pi} \langle -\sin t, \, \cos t, \, 0 \rangle \cdot \langle - \sin t, \, 0, \, \cos t \rangle \, dt \\[4pt] &= \int_0^{2\pi} \sin^2 t \, dt \\[4pt] &= \pi. \end{align*}\]

Por la ecuación para integrales de líneas vectoriales,

\[ \begin{align*} \iint_S \, curl \, \vecs{F} \cdot d\vecs S &= \iint_D curl \, \vecs{F} (\vecs r (\phi,\theta)) \cdot ( \vecs t_{\phi} \times \vecs t_{\theta}) \, dA \\[4pt] &= \iint_D \langle 0, -1, 1 \rangle \cdot \langle \cos \theta \, \sin^2 \phi, \, \sin \theta \, \sin^2 \phi, \, \sin \phi \, \cos \phi \rangle \, dA \\[4pt] &= \int_0^{\pi} \int_0^{\pi} (\sin \phi \, \cos \phi - \sin \theta \, \sin^2 \phi ) \, d\phi d\theta \\[4pt] &= \dfrac{\pi}{2} \int_0^{\pi} \sin \theta \, d\theta \\[4pt] &= \pi.\end{align*}\]

Por lo tanto, hemos verificado el teorema de Stokes para este ejemplo.

Ejercicio\(\PageIndex{1}\)

Verificar que el teorema de Stokes es verdadero para el campo vectorial\(\vecs{F}(x,y,z) = \langle y,x,-z \rangle \) y la superficie\(S\), donde\(S\) está la porción orientada hacia arriba de la gráfica de\(f(x,y) = x^2 y\) sobre un triángulo en el\(xy\) plano -con vértices\((0,0), \, (2,0)\), y\((0,2)\).

Pista

Calcule la integral doble y la integral de línea por separado.

Contestar

Ambas integrales dan\(-\dfrac{136}{45}\):

Aplicando el Teorema de Stokes

El teorema de Stokes se traduce entre la integral de flujo de la superficie\(S\) a una integral de línea alrededor del límite de\(S\). Por lo tanto, el teorema nos permite calcular integrales superficiales o integrales de línea que ordinariamente serían bastante difíciles al traducir la integral de línea en una integral de superficie o viceversa. Ahora estudiamos algunos ejemplos de cada tipo de traducción.

Ejemplo\(\PageIndex{2}\): Calculating a Surface Integral

Calcular integral de superficie

\[\iint_S curl \, \vecs{F} \cdot d\vecs S, \nonumber \]

donde\(S\) está la superficie, orientada hacia afuera, en la Figura\(\PageIndex{6}\) y\(\vecs{F} = \langle z,\, 2xy, \, x + y \rangle\).

Figura\(\PageIndex{6}\): Una superficie complicada en un campo vectorial.

Solución

Tenga en cuenta que para calcular

\[ \iint_S curl \, \vecs F \cdot d\vecs S \nonumber \]

sin usar el teorema de Stokes, necesitaríamos la ecuación para integrales de superficie escalar. El uso de esta ecuación requiere una parametrización de\(S\). \(S\)La superficie es lo suficientemente complicada como para que sea extremadamente difícil encontrar una parametrización. Por lo tanto, los métodos que hemos aprendido en secciones anteriores no son útiles para este problema. En cambio, usamos el teorema de Stokes, señalando que el límite\(C\) de la superficie es simplemente un solo círculo con radio 1.

El rizo de\(\vecs{F}\) es\(\langle 1,1,2y \rangle\). Por el teorema de Stokes,

\[\iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r, \nonumber \]

donde\(C\) tiene parametrización\(\langle \cos t, \, \sin t, \, 1 \rangle, 0 \leq t \leq 2\pi\). Por la ecuación para integrales de líneas vectoriales,

\[ \begin{align*} \iint_S curl \, F \cdot d\vecs S &= \int_C \vecs{F} \cdot d \vecs{r} \\[4pt] &= \int_0^2 \langle 1, \, \sin t \, \cos t, \, \cos t + \sin t \rangle \cdot \langle - \sin t, \, \cos t, \, 0 \rangle \, dt \\[4pt] &= \int_0^{2\pi} ( - \sin t + 2 \, \sin t \, \cos^2 t ) \, dt \\[4pt] &= \left[ \cos t - \dfrac{2 \, \cos^3 t}{3} \right]_0^{2\pi} \\[4pt] &= \cos (2\pi) - \dfrac{2 \, \cos^3 (2\pi)}{3} - \left(\cos (0) - \dfrac{2 \, \cos^3 (0)}{3} \right) \\[4pt] &= 0. \end{align*} \nonumber \]

Una consecuencia sorprendente del teorema de Stokes es que si\(S'\) hay alguna otra superficie lisa con límite\(C\) y la misma orientación que\(S\), entonces\[\iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r = 0 \nonumber \] porque el teorema de Stokes dice que la integral de superficie depende de la línea integral alrededor del límite solamente.

En Ejemplo\(\PageIndex{2}\), calculamos una integral de superficie simplemente usando información sobre el límite de la superficie. En general, dejar\(S_1\) y\(S_2\) ser superficies lisas con el mismo límite\(C\) y la misma orientación. Por el teorema de Stokes,

\[\iint_{S_1} curl \, \vecs{F} \cdot d\vecs{S} = \int_C \vecs{F} \cdot d\vecs{r} = \iint_{S_2} curl \, \vecs{F} \cdot d\vecs{S}. \label{20} \]

Por lo tanto, si

\[\iint_{S_1} curl \, \vecs{F} \cdot d\vecs{S} \nonumber \]

es difícil de calcular pero

\[\iint_{S_2} curl \, \vecs{F} \cdot d\vecs S \nonumber \]

es fácil de calcular, el teorema de Stokes nos permite calcular la integral de superficie más fácil. En Ejemplo\(\PageIndex{2}\), podríamos haber calculado

\[\iint_S curl \, \vecs{F} \cdot d \vecs{S} \nonumber \]

calculando

\[\iint_{S'} curl \, \vecs{F} \cdot d\vecs{S}, \nonumber \]

donde\(\vecs{S}'\) está el disco encerrado por curva límite\(C\) (una superficie mucho más simple con la que trabajar).

La ecuación\ ref {20} muestra que las integrales de flujo de los campos de vector curl son independientes de la superficie de la misma manera que las integrales de línea de los campos de gradiente son independientes de la ruta. Recordemos que si\(\vecs{F}\) es un campo vectorial conservador bidimensional definido en un dominio simplemente conectado,\(f\) es una función potencial para\(\vecs{F}\), y\(C\) es una curva en el dominio de\(\vecs{F}\), entonces

\[\int_C \vecs{F} \cdot d\vecs{r} \nonumber \]

depende únicamente de los puntos finales de\(C\). Por lo tanto, si\(C'\) hay alguna otra curva con el mismo punto de partida y punto final que\(C\) (es decir,\(C'\) tiene la misma orientación que\(C\)), entonces

\[\int_C \vecs{F} \cdot d\vecs{r} = \int_{C'} \vecs{F} \cdot d\vecs{r} \nonumber \]

En otras palabras, el valor de la integral depende únicamente del límite del camino; realmente no depende del camino mismo.

Análogamente, supongamos que\(S\) y\(S'\) son superficies con el mismo límite y la misma orientación, y supongamos que\(\vecs{G}\) es un campo vectorial tridimensional que puede escribirse como el rizo de otro campo vectorial\(\vecs{F}\) (así que\(\vecs{F}\) es como un “campo potencial” de\(\vecs{G}\)). Por Ecuación\ ref {20},

\[ \begin{align*} \iint_S \vecs G \cdot d\vecs S = \iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r = \iint_{S'} curl \, \vecs F \cdot d\vecs S = \iint_{S'} \vecs G \cdot d\vecs S.\end{align*} \nonumber \]

Por lo tanto, la integral de flujo de\(\vecs{G}\) no depende de la superficie, solo del límite de la superficie. Las integrales de flujo de los campos vectoriales que se pueden escribir como el curl de un campo vectorial son independientes de la superficie de la misma manera que las integrales de línea de los campos vectoriales que se pueden escribir como el gradiente de una función escalar son independientes de la ruta.

Ejercicio\(\PageIndex{1}\)

Utilice el teorema de Stokes para calcular la integral de superficie\[\iint_S curl \, \vecs{F} \cdot d\vecs{S}, \nonumber \] donde\(\vecs{F} = \langle x,y,z \rangle\) y\(S\) es la superficie como se muestra en la siguiente figura.

Pista

Parametrizar el límite de\(S\) and translate to a line integral.

Answer

\(-\pi\)

Example \(\PageIndex{3}\): Calculating a Line Integral

Calculate the line integral

\[\int_C \vecs{F} \cdot d\vecs{r}, \nonumber \]

where \(\vecs{F} = \langle xy, \, x^2 + y^2 + z^2, \, yz \rangle\) and \(C\) is the boundary of the parallelogram with vertices \((0,0,1), \, (0,1,0), \, (2,0,-1)\), and \((2,1,-2)\).

Solution

To calculate the line integral directly, we need to parameterize each side of the parallelogram separately, calculate four separate line integrals, and add the result. This is not overly complicated, but it is time-consuming.

By contrast, let’s calculate the line integral using Stokes’ theorem. Let \(S\) denote the surface of the parallelogram. Note that \(S\) is the portion of the graph of \(z = 1 - x - y\) for \((x,y)\) varying over the rectangular region with vertices \((0,0), \, (0,1), \, (2,0)\), and \((2,1)\) in the \(xy\)-plane. Therefore, a parameterization of \(S\) is \(\langle x,y, \, 1 - x - y \rangle, \, 0 \leq x \leq 2, \, 0 \leq y \leq 1\). The curl of \(\vecs{F}\) is \( \langle -z, \, 0, \, x \rangle\),and Stokes’ theorem and the equation for scalar surface integrals

\[ \begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &= \iint_S curl \, \vecs{F} \cdot d\vecs{S} \\[4pt] &= \int_0^2 \int_0^1 curl \, \vecs{F} (x,y) \cdot (\vecs t_x \times \vecs t_y) \, dy\, dx \\[4pt] &= \int_0^2 \int_0^1 \langle - (1 - x - y), \, 0, \, x \rangle \cdot ( \langle 1, \, 0, -1 \rangle \times \langle 0, \, 1, \, -1 \rangle ) \, dy \,dx \\[4pt] &= \int_0^2 \int_0^1 \langle x + y - 1, \, 0, \, x \rangle \cdot \langle 1, 1, 1 \rangle \, dy \, dx \\[4pt] &= \int_0^2 \int_0^1 2x + y - 1 \, dy \, dx \\[4pt] &= 3.\end{align*} \nonumber \]

Exercise \(\PageIndex{3}\)

Use Stokes’ theorem to calculate line integral

\[\int_C \vecs{F} \cdot d\vecs{r}, \nonumber \]

where \(\vecs{F} = \langle z,x,y \rangle \) and \(C\) is the boundary of a triangle with vertices \((0,0,1), \, (3,0,-2)\), and \((0,1,2)\).

Hint

This triangle lies in plane \(z = 1 - x + y\).

Answer

\(\dfrac{3}{2}\)

Interpretation of Curl

In addition to translating between line integrals and flux integrals, Stokes’ theorem can be used to justify the physical interpretation of curl that we have learned. Here we investigate the relationship between curl and circulation, and we use Stokes’ theorem to state Faraday’s law—an important law in electricity and magnetism that relates the curl of an electric field to the rate of change of a magnetic field.

Recall that if \(C\) is a closed curve and \(\vecs{F}\) is a vector field defined on \(C\), then the circulation of \(\vecs{F}\) around \(C\) is line integral

\[\int_C \vecs{F} \cdot d\vecs{r}. \nonumber \]

If \(\vecs{F}\) represents the velocity field of a fluid in space, then the circulation measures the tendency of the fluid to move in the direction of \(C\).

Let \(\vecs{F}\) be a continuous vector field and let \(D_{\tau}\) be a small disk of radius \(r\) with center \(P_0\) (Figure \(\PageIndex{7}\)). If \(D_{\tau}\) is small enough, then \((curl \, \vecs{F})(P) \approx (curl \, \vecs F)(P_0)\) for all points \(P\) in \(D_{\tau}\) because the curl is continuous. Let \(C_{\tau}\) be the boundary circle of \(D_{\tau}\): By Stokes’ theorem,

\[\int_{C_{\tau}} \vecs{F} \cdot d\vecs{r} = \iint_{D_{\tau}} curl \, \vecs{F} \cdot \vecs{N} \, d\vecs S \approx \iint_{D_{\tau}} (curl \, \vecs{F})(P_0) \cdot \vecs{N} (P_0) \, d\vecs S. \nonumber \]

Figure \(\PageIndex{7}\): Disk \(D_{\tau}\) is a small disk in a continuous vector field.

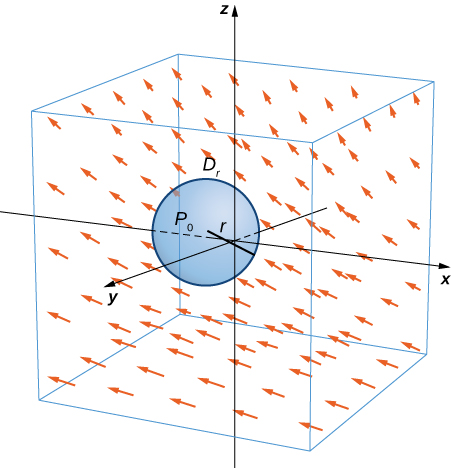
The quantity \( (curl \, \vecs F)(P_0) \cdot \vecs N (P_0) \) is constant, and therefore

\[\iint_{D_{\tau}} (curl \, \vecs F)(P_0) \cdot \vecs N (P_0) \, d\vecs S = \pi r^2 [(curl \, \vecs F)(P_0) \cdot \vecs N (P_0)]. \nonumber \]

Thus

\[\int_{C_{\tau}} \vecs F \cdot d\vecs r \approx \pi r^2 [ (curl \, \vecs F)(P_0) \cdot \vecs N (P_0)], \nonumber \]

and the approximation gets arbitrarily close as the radius shrinks to zero. Therefore Stokes’ theorem implies that

\[(curl \, \vecs F)(P_0) \cdot \vecs N (P_0) = \lim_{r\rightarrow 0^+} \dfrac{1}{\pi r^2} \int_{C_{\tau}} \vecs F \cdot d\vecs r. \nonumber \]

This equation relates the curl of a vector field to the circulation. Since the area of the disk is \(\pi r^2\), this equation says we can view the curl (in the limit) as the circulation per unit area. Recall that if \(\vecs F\) is the velocity field of a fluid, then circulation \[\oint_{C_{\tau}} \vecs F \cdot d\vecs r = \oint_{C_{\tau}} \vecs F \cdot \vecs T \, ds \nonumber \] is a measure of the tendency of the fluid to move around \(C_{\tau}\): The reason for this is that \(\vecs F \cdot \vecs T\) is a component of \(\vecs F\) in the direction of \(\vecs T\), and the closer the direction of \(\vecs F\) is to \(\vecs T\), the larger the value of \(\vecs F \cdot \vecs T\) (remember that if \(\vecs a\) and \(\vecs b\) are vectors and \(\vecs b\) is fixed, then the dot product \(\vecs a \cdot \vecs b\) is maximal when \(\vecs a\) points in the same direction as \(\vecs b\)). Therefore, if \(\vecs F\) is the velocity field of a fluid, then \(curl \, \vecs F \cdot \vecs N\) is a measure of how the fluid rotates about axis \(\vecs N\). The effect of the curl is largest about the axis that points in the direction of \(\vecs N\), because in this case \(curl \, \vecs F \cdot \vecs N\) is as large as possible.

To see this effect in a more concrete fashion, imagine placing a tiny paddlewheel at point \(P_0\) (Figure \(\PageIndex{8}\)). The paddlewheel achieves its maximum speed when the axis of the wheel points in the direction of curl \(\vecs F\). This justifies the interpretation of the curl we have learned: curl is a measure of the rotation in the vector field about the axis that points in the direction of the normal vector \(\vecs N\), and Stokes’ theorem justifies this interpretation.

Figure \(\PageIndex{8}\): To visualize curl at a point, imagine placing a tiny paddlewheel at that point in the vector field.

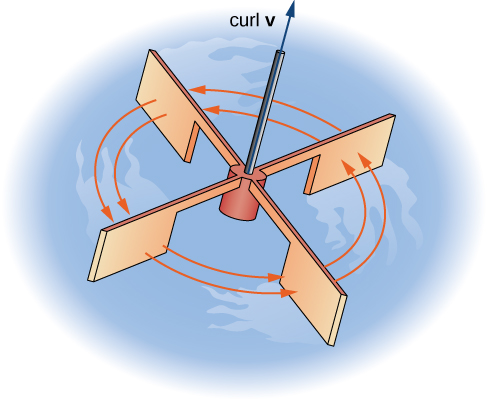
Now that we have learned about Stokes’ theorem, we can discuss applications in the area of electromagnetism. In particular, we examine how we can use Stokes’ theorem to translate between two equivalent forms of Faraday’s law. Before stating the two forms of Faraday’s law, we need some background terminology.

Let \(C\) be a closed curve that models a thin wire. In the context of electric fields, the wire may be moving over time, so we write \(C(t)\) to represent the wire. At a given time \(t\), curve \(C(t)\) may be different from original curve \(C\) because of the movement of the wire, but we assume that \(C(t)\) is a closed curve for all times \(t\). Let \(D(t)\) be a surface with \(C(t)\) as its boundary, and orient \(C(t)\) so that \(D(t)\) has positive orientation. Suppose that \(C(t)\)is in a magnetic field \(\vecs B(t)\) that can also change over time. In other words, \(\vecs{B}\) has the form

\[\vecs B(x,y,z) = \langle P(x,y,z), \, Q(x,y,z), \, R(x,y,z) \rangle, \nonumber \]

where \(P\), \(Q\), and \(R\) can all vary continuously over time. We can produce current along the wire by changing field \(\vecs B(t)\) (this is a consequence of Ampere’s law). Flux \(\displaystyle \phi (t) = \iint_{D(t)} \vecs B(t) \cdot d\vecs S\) creates electric field \(\vecs E(t)\) that does work. The integral form of Faraday’s law states that

\[Work = \int_{C(t)} \vecs E(t) \cdot d\vecs r = - \dfrac{\partial \phi}{\partial t}. \nonumber \]

In other words, the work done by \(\vecs{E}\) is the line integral around the boundary, which is also equal to the rate of change of the flux with respect to time. The differential form of Faraday’s law states that

\[curl \, \vecs{E} = - \dfrac{\partial \vecs B}{\partial t}. \nonumber \]

Using Stokes’ theorem, we can show that the differential form of Faraday’s law is a consequence of the integral form. By Stokes’ theorem, we can convert the line integral in the integral form into surface integral

\[-\dfrac{\partial \phi}{\partial t} = \int_{C(t)} \vecs E(t) \cdot d\vecs r = \iint_{D(t)} curl \,\vecs E(t) \cdot d\vecs S. \nonumber \]

Since \[\phi (t) = \iint_{D(t)} B(t) \cdot d\vecs S, \nonumber \] then as long as the integration of the surface does not vary with time we also have

\[- \dfrac{\partial \phi}{\partial t} = \iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S. \nonumber \]

Therefore,

\[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \,\vecs E \cdot d\vecs S. \nonumber \]

To derive the differential form of Faraday’s law, we would like to conclude that \(curl \,\vecs E = -\dfrac{\partial \vecs B}{\partial t}\): In general, the equation

\[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \,\vecs E \cdot d\vecs S \nonumber \]

is not enough to conclude that \(curl \, \vecs E = -\dfrac{\partial \vecs B}{\partial t}\): The integral symbols do not simply “cancel out,” leaving equality of the integrands. To see why the integral symbol does not just cancel out in general, consider the two single-variable integrals \(\displaystyle \int_0^1 x \, dx\) and \(\displaystyle \int_0^1 f(x)\, dx\), where

\[f(x) = \begin{cases}1, &\text{if } 0 \leq x \leq 1/2 \\ 0, & \text{if } 1/2 \leq x \leq 1. \end{cases} \nonumber \]

Both of these integrals equal \(\dfrac{1}{2}\), so \(\displaystyle \int_0^1 x \, dx = \int_0^1 f(x) \, dx\).

However, \(x \neq f(x)\). Analogously, with our equation \[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \, \vecs E \cdot d\vecs S, \nonumber \] we cannot simply conclude that \(curl \, \vecs E = -\dfrac{\partial \vecs B}{\partial t}\) just because their integrals are equal. However, in our context, equation

\[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \, \vecs E \cdot d\vecs S \nonumber \]

is true for any region, however small (this is in contrast to the single-variable integrals just discussed). If \(\vecs F\) and \(\vecs G\) are three-dimensional vector fields such that

\[\iint_S \vecs F \cdot d\vecs S = \iint_S \vecs G \cdot d\vecs S \nonumber \]

for any surface \(S\), then it is possible to show that \(\vecs F = \vecs G\) by shrinking the area of \(S\) to zero by taking a limit (the smaller the area of \(S\), the closer the value of \(\displaystyle \iint_S \vecs F \cdot d\vecs S\) to the value of \(\vecs F\) at a point inside \(S\)). Therefore, we can let area \(D(t)\) shrink to zero by taking a limit and obtain the differential form of Faraday’s law:

\[curl \,\vecs E = - \dfrac{\partial \vecs B}{\partial t}. \nonumber \]

In the context of electric fields, the curl of the electric field can be interpreted as the negative of the rate of change of the corresponding magnetic field with respect to time.

Example \(\PageIndex{4}\): Using Faraday’s Law

Calculate the curl of electric field \(\vecs{E}\) if the corresponding magnetic field is constant field \(\vecs B(t) = \langle 1, -4, 2 \rangle\).

Solution

Since the magnetic field does not change with respect to time, \(-\dfrac{\partial \vecs B}{\partial t} = \vecs 0\). By Faraday’s law, the curl of the electric field is therefore also zero.

Analysis

A consequence of Faraday’s law is that the curl of the electric field corresponding to a constant magnetic field is always zero.

Exercise \(\PageIndex{4}\)

Calculate the curl of electric field \(\vecs{E}\) if the corresponding magnetic field is \(\vecs B(t) = \langle tx, \, ty, \, -2tz \rangle, \, 0 \leq t < \infty.\)

Hint

• Use the differential form of Faraday’s law.
• Notice that the curl of the electric field does not change over time, although the magnetic field does change over time.

Answer

\(curl \, \vecs{E} = \langle x, \, y, \, -2z \rangle\)

Key Concepts

• Stokes’ theorem relates a flux integral over a surface to a line integral around the boundary of the surface. Stokes’ theorem is a higher dimensional version of Green’s theorem, and therefore is another version of the Fundamental Theorem of Calculus in higher dimensions.
• Stokes’ theorem can be used to transform a difficult surface integral into an easier line integral, or a difficult line integral into an easier surface integral.
• Through Stokes’ theorem, line integrals can be evaluated using the simplest surface with boundary \(C\).
• Faraday’s law relates the curl of an electric field to the rate of change of the corresponding magnetic field. Stokes’ theorem can be used to derive Faraday’s law.

Key Equations

• Stokes’ theorem

\[\int_C \vecs{F} \cdot d\vecs{r} = \iint_S curl \, \vecs{F} \cdot d\vecs{S} \nonumber \]

Glossary

Stokes’ theorem

relates the flux integral over a surface \(S\) to a line integral around the boundary \(C\) of the surface \(S\)

surface independent

flux integrals of curl vector fields are surface independent if their evaluation does not depend on the surface but only on the boundary of the surface