5: Probabilidad
- Page ID
- 82084
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Hemos estado considerando un modelo de un sistema de manejo de información en el que los símbolos de una entrada se codifican en bits, que luego se envían a través de un “canal” a un receptor y se vuelven a decodificar en símbolos. Ver Figura 5.1.
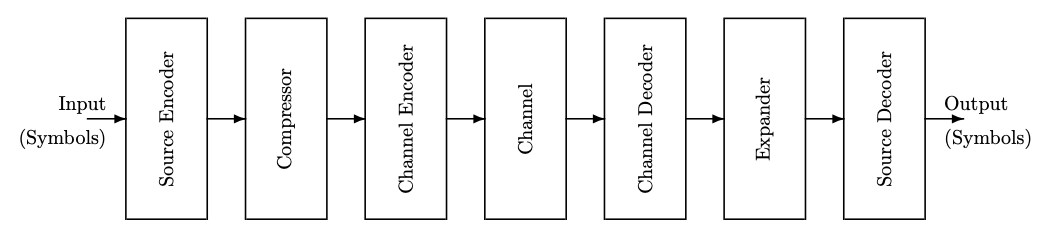
En capítulos anteriores de estas notas hemos mirado diversos componentes de este modelo. Ahora volvemos a la fuente y la modelizamos de manera más completa, en términos de distribuciones de probabilidad.
La fuente proporciona un símbolo o una secuencia de símbolos, seleccionados de algún conjunto. El proceso de selección puede ser un experimento, como voltear una moneda o rodar dados. O podría ser la observación de acciones no provocadas por el observador. O la secuencia de símbolos podría ser de una representación de algún objeto, como caracteres de texto, o píxeles de una imagen.
Consideramos solo casos con un número finito de símbolos para elegir, y solo casos en los que los símbolos son ambos mutuamente excluyentes (solo se puede elegir uno a la vez) y exhaustivos (uno es realmente elegido). Cada elección constituye un “resultado” y nuestro objetivo es rastrear la secuencia de resultados, y la información que los acompaña, a medida que la información viaja de la entrada a la salida. Para ello, necesitamos poder decir cuál es el resultado, y también nuestro conocimiento sobre algunas propiedades del resultado.
Si conocemos el resultado, tenemos una manera perfectamente buena de denotar el resultado. Podemos simplemente nombrar al símbolo elegido, e ignorar el resto de los símbolos, que no fueron elegidos. Pero, ¿y si aún no conocemos el resultado, o somos inciertos en algún grado? ¿Cómo se supone que debemos expresar nuestro estado de conocimiento si hay incertidumbre? Utilizaremos las matemáticas de probabilidad para este propósito.
Para ilustrar esta importante idea, utilizaremos ejemplos basados en las características de los estudiantes del MIT. El recuento oficial de alumnos en el MIT\(^1\) para el otoño de 2007 incluye los datos en la Tabla 5.1, que se reproduce en formato de diagrama de Venn en la Figura 5.2.
| Mujeres | Hombres | Total | |
| Estudiantes de primer año | 496 | 577 | 1,073 |
| Graduados | 1,857 | 2,315 | 4,172 |
| Estudiantes de Posgrado | 1,822 | 4,226 | 6,048 |
| Total Alumnos | 3,679 | 6,541 | 10,220 |
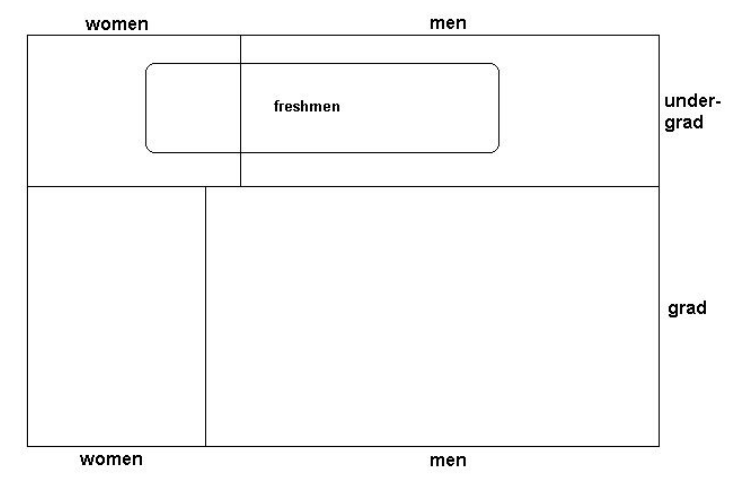
Supongamos que se selecciona un estudiante de primer año del MIT (el símbolo que se elige es un estudiante individual, y el conjunto de símbolos posibles son los estudiantes de primer año de 1073), y no se le informa quién es. Te preguntas si es una mujer o un hombre. Por supuesto que si conocieras la identidad del alumno seleccionado, sabrías el género. Pero si no, ¿cómo podrías caracterizar tus conocimientos? ¿Cuál es la probabilidad, o probabilidad, de que se haya seleccionado a una mujer?
Tenga en cuenta que 46% de la clase de primer año de 2007 (496/1,073) son mujeres. Se trata de un hecho, o una estadística, que puede representar o no la probabilidad de que el estudiante de primer año elegido sea una mujer. Si tuvieras razones para creer que todos los estudiantes de primer año tenían la misma probabilidad de ser elegidos, podrías decidir que la probabilidad de que sea mujer es del 46%. Pero, ¿y si te dicen que la selección se hace en el pasillo de McCormick Hall (un dormitorio de mujeres)? En ese caso la probabilidad de que el estudiante de primer año elegido sea una mujer probablemente sea superior al 46%. Tanto las estadísticas como las probabilidades pueden describirse usando las mismas matemáticas (que se desarrollarán a continuación), pero son cosas diferentes.
\(^1\)todas las alumnas: http://web.mit.edu/registrar/www/sta...portfinal.html, todas las mujeres: http://web.mit.edu/registrar/www/sta...omenfinal.html