6.4: Modelo de canal

Última actualización
Guardar como PDF

Page ID: 81994

Paul Penfield, Jr.
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Un canal de comunicación acepta bits de entrada y produce bits de salida. Modelamos la entrada como la selección de uno de un número finito de estados de entrada (para el canal más simple, dos de tales estados), y la salida como un evento similar. El lenguaje de la teoría de la probabilidad será útil para describir los canales. Si el canal cambia perfectamente su estado de salida en conformidad con su estado de entrada, se dice que no tiene ruido y en ese caso nada afecta a la salida excepto la entrada. Digamos que el canal tiene una cierta velocidad máxima\(W\) a la que su salida puede seguir los cambios en la entrada (así como la fuente tiene una velocidad\(R\) a la que se seleccionan los símbolos).

Usaremos el índice\(i\) para repasar los estados de entrada y\(j\) para indexar los estados de salida. Nos referiremos a los eventos de entrada como\(A_i\) y a los eventos de salida como\(B_j\). Puede imaginar el canal como algo con entradas y salidas, como en la Figura 6.3, pero tenga en cuenta que las entradas no son entradas de señal normales o entradas eléctricas a los sistemas, sino eventos mutuamente excluyentes, solo uno de los cuales es cierto en cualquier momento. Para canales simples tal diagrama es simple porque hay tan pocas opciones posibles, pero para estructuras más complicadas puede haber tantas entradas posibles que los diagramas se vuelven poco prácticos (aunque pueden ser útiles como modelo conceptual). Por ejemplo, una puerta lógica con tres entradas, cada una de las cuales podría ser 0 o 1, tendría ocho entradas en un diagrama de este tipo. El canal binario tiene dos estados de entrada mutuamente excluyentes y es el que se muestra en la Figura 6.3.

Para un canal sin ruido, donde cada uno de los\(n\) posibles estados de entrada conduce a exactamente un estado de salida, cada nuevo estado de entrada (\(R\)por segundo) se puede especificar con\(\log_2 n\) bits. Así, para el canal binario,\(n\) = 2, y así el nuevo estado se puede especificar con un bit. La velocidad máxima a la que la información suministrada a la entrada puede

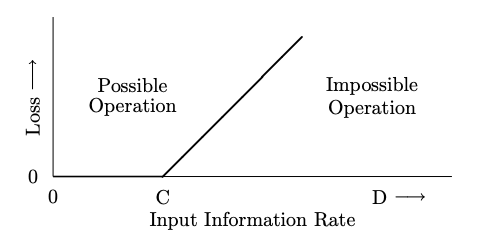
Screen Shot 2021-05-05 a las 11.11.25 PM.png — Figura 6.4: Diagrama de pérdida de canal. Para una velocidad de datos de entrada\(D\), ya sea menor o mayor que la capacidad del canal\(C\), la velocidad mínima posible a la que se pierde información es la mayor de 0 y\(D − C\)

afectar la salida se llama la capacidad del canal\(C = W \log_2 n\) bits por segundo. Para el canal binario,\(C = W\).

Si la entrada se cambia a una velocidad\(R\) menor que\(W\) (o, de manera equivalente, si la información suministrada en la entrada es menor que\(C\)) entonces la salida puede seguir a la entrada, y los eventos de salida se pueden usar para inferir la identidad de los símbolos de entrada a esa velocidad. Si hay un intento de cambiar la entrada más rápidamente, el canal no puede seguir (ya que\(W\) es por definición la velocidad máxima a la que los cambios en la entrada afectan a la salida) y parte de la información de entrada se pierde.