7.2: Diagramas de probabilidad

El modelo de probabilidad de un proceso con\(n\) entradas y\(m\) salidas, donde\(n\) y\(m\) son enteros, se muestra en la Figura 7.5. Los estados\(n\) de entrada son mutuamente excluyentes, al igual que los estados\(m\) de salida. Si este proceso es implementado por puertas lógicas, la entrada necesitaría al menos\(\log_2(n)\) pero no tantos como\(n\) cables.

Figura 7.3: Modelo de probabilidad de una puerta de dos entradas y una salida.

Figura 7.4: Modelo de probabilidad de una\(AND\) puerta

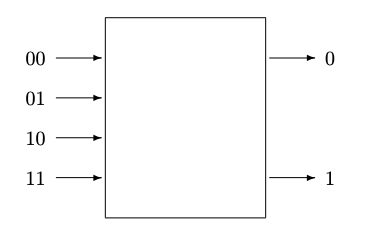
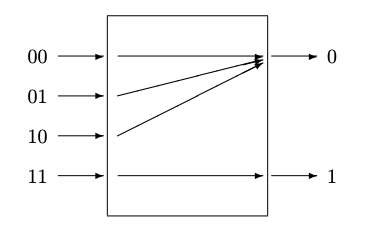
Este modelo de procesos es conceptualmente simple y general. Funciona bien para procesos con un pequeño número de bits. Se utilizó para el canal binario en el Capítulo 6.

Desafortunadamente, el modelo de probabilidad es incómodo cuando el número de bits de entrada es moderado o grande. La razón es que las entradas y salidas se representan en términos de conjuntos de eventos mutuamente excluyentes. Si los eventos describen señales en, digamos, cinco cables, cada uno de los cuales puede llevar un voltaje alto o bajo que significa un booleano 1 o 0, habría 32 eventos posibles. Es mucho más fácil dibujar una puerta lógica, con cinco entradas que representan variables físicas, que un proceso de probabilidad con 32 estados de entrada. Esta “explosión exponencial” del número de posibles estados de entrada se vuelve aún más severa cuando el proceso representa la evolución del estado de un sistema físico con un gran número de átomos. Por ejemplo, el número de moléculas en un mol de gas es el número de Avogadro\(N_A = 6.02 × 10^{23}\). Si cada átomo tuviera solo una variable booleana asociada, habría 2\(^{N_A}\) estados, mucho mayor que el número de partículas en el universo. Y no habría tiempo para siquiera enumerar todas las partículas, mucho menos hacer algún cálculo: el número de microsegundos ya que el big bang es menor a 5 × 10\(^{23}\). A pesar de esta limitación, el modelo de diagrama de probabilidad es útil conceptualmente.

Revisemos las ideas fundamentales en las comunicaciones, introducidas en el Capítulo 6, en el contexto de tales diagramas.

Suponemos que cada posible estado de entrada de un proceso puede conducir a uno o más estados de salida. Para cada

Figura 7.5: Modelo de probabilidad

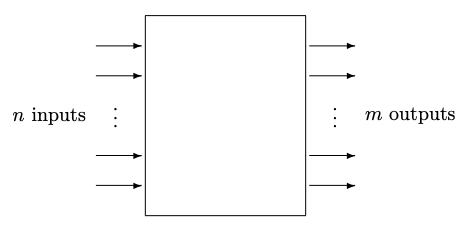
entrada\(i\) denotan la probabilidad de que esta entrada conduzca a la salida\(j\) como\(c_{ji}\). Estas probabilidades de transición se\(c_{ji}\) pueden considerar como una tabla, o matriz, con tantas columnas como estados de entrada haya, y tantas filas como estados de salida. Utilizaremos\(i\) como índice sobre los estados de entrada y\(j\) sobre los estados de salida, y denotaremos el evento asociado con la selección de entrada\(i\) como\(A_i\) y el evento asociado con la salida\(j\) como\(B_j\).

Las probabilidades de transición son propiedades del proceso, y no dependen de las entradas al proceso. Las probabilidades de transición se encuentran entre 0 y 1, y para cada uno\(i\) su suma sobre el índice de salida\(j\) es 1, ya que para cada posible evento de entrada ocurre exactamente un evento de salida. Si el número de estados de entrada es el mismo que el número de estados de salida entonces\(c_{ji}\) es una matriz cuadrada; de lo contrario, tiene más columnas que filas o viceversa.

\(0 \leq c_{ji} \leq 1 \tag{7.1}\)

\(1 = \displaystyle \sum_{j} c_{ji} \tag{7.2}\)

Esta descripción tiene gran generalidad. Se aplica a un proceso determinista (aunque puede no ser el más conveniente, una tabla de verdad que da la salida para cada una de las entradas suele ser más sencilla de pensar). Para tal proceso, cada columna de la\(c_{ji}\) matriz contiene un elemento que es 1 y todos los demás elementos son 0. También se aplica a un canal no determinista (es decir, uno con ruido). Se aplica al codificador y decodificador fuente, al compresor y expansor, y al codificador y decodificador de canal. Se aplica a puertas lógicas y a dispositivos que realizan cálculos arbitrarios sin memoria (a veces llamada “lógica combinacional” en distinción de “lógica secuencial” que puede involucrar estados anteriores). Incluso se aplica a las transiciones tomadas por un sistema físico de uno de sus estados al siguiente. Se aplica si el número de estados de salida es mayor que el número de estados de entrada (por ejemplo, codificadores de canal) o menor (por ejemplo, decodificadores de canal).

Si una entrada de proceso está determinada por eventos aleatorios\(A_i\) con distribución de probabilidad\(p(A_i)\), entonces se pueden calcular las otras probabilidades. Las probabilidades de salida condicionales, condicionadas a la entrada, son

\(p(B_j \; |\; A_i) = c_{ji} \tag{7.3}\)

La probabilidad incondicional de cada salida\(p(B_j)\) es

\(p(B_j = \displaystyle \sum_{i} c_{ji}p(A_i) \tag{7.4}\)

Finalmente, la probabilidad conjunta de cada entrada con cada salida\(p(A_i, B_j)\) y las probabilidades condicionales hacia atrás se\(p(A_i \;|\; B_j)\) pueden encontrar usando el Teorema de Bayes:

\[\begin{align*} p(A_i, B_j) & = p(B_j)p(A_i \;|\; B_j) \tag{7.5} \\ & = p(A_i)p(B_j \;|\; A_i) \tag{7.6} \\ & = p(A_i)c_{ji} \tag{7.7} \end{align*} \]