6: Rango y Resistencia

Última actualización
Guardar como PDF

Page ID: 80893

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Introducción

Un poco de fondo

En los primeros días del vuelo motorizado, la principal preocupación era hacer que la aeronave saliera al aire y volviera a bajar de manera segura (lo que significa con seguridad la capacidad de alejarse cojeando después del “aterrizaje”). El famoso primer vuelo del Wright fue más corto que un campo de fútbol e incluso durante un par de años después de diciembre de 1903 se contentaron con dar la vuelta a la granja familiar Los motores construidos en casa de Wright no podían funcionar durante largos períodos de tiempo y simplemente no vislumbraban la necesidad o el deseo de volar distancias de más de unos pocos kilómetros. En 1908, sin embargo, la revista Scientific American desafió a los experimentadores de aviación a producir un avión o “avión” ^[1] que pudiera volar, a la vista del público, ¡a una distancia de una milla! Si bien los Wright afirmaron poder realizar tal vuelo, su obsesión por el secreto mientras buscaban ventas militares y su creencia egoísta de que nadie más podía acercarse a su experiencia en aviación los llevó a ignorar el premio ofrecido por Scientific American para el vuelo público de una milla.

Fue Glenn Curtiss, un constructor de motores de motocicleta y poseedor de numerosos récords mundiales de velocidad en las carreras de motocicletas, quien, en julio de 1908, realizó el primer vuelo público de una milla. Curtiss, que había trabajado con Alexander Bell y otros para desarrollar sus propios aviones, realizó el vuelo con reporteros de periódicos mirando y con cámaras de películas que grababan el vuelo. Curtiss se convirtió en el mejor aviador de América y los Wrights estaban furiosos, lo que dio lugar a numerosos juicios ya que Wilbur y Orville buscaron demostrar en los tribunales que Curtiss y Bell habían infringido sus patentes. Curtiss pasó a superar a los Wghts y a otros en los eventos de aviación en América y Europa. Las posteriores demandas de patentes de Wright destinadas a reservarse los únicos derechos para diseñar y construir aviones en Estados Unidos estancaron el desarrollo de aviones en América y trasladaron la escena del progreso aeronáutico a Europa donde permaneció hasta después de la Primera Guerra Mundial.

A medida que los aviones y la aviación continuaron desarrollándose, el alcance y la resistencia se convirtieron en el objetivo principal en el diseño En la guerra, los bombarderos necesitaban largos alcances para alcanzar objetivos enemigos más allá de las líneas del frente y al final de la Primera Guerra Mundial se habían desarrollado enormes bombarderos en varios países. Después de la guerra, los gobiernos europeos subsidiaron la conversión de estos gigantes en aviones de pasajeros. Algunos aviones más grandes incluso se habían construido como vehículos de transporte de pasajeros antes del conflicto. Los primeros diseños de Sikorski son buenos ejemplos. En Estados Unidos, sin embargo, con poco interés gubernamental en promover los viajes aéreos para el público hasta finales de la década de 1920, el desarrollo de aviones de largo alcance era más fantasía que hecho. En 1927 el vuelo transatlántico de Lindberg capturó la imaginación del público y aumentó el interés por los vuelos de largo alcance. El vuelo de Lindberg, al igual que el de Curtiss, fue impulsado por un premio de los medios impresos, ilustrando el papel de periódicos y revistas para impulsar el progreso tecnológico.

A finales de la década de 1930 el público comenzó a ver el vuelo como una forma de viajar largas distancias en tiempos cortos, se habían desarrollado rutas aéreas nacionales e internacionales, y aviones como el “China Clipper” establecieron estándares de alcance y resistencia. La Segunda Guerra Mundial obligó a la gente y a los gobiernos a pensar en términos globales que condujeron al desarrollo en tiempos de guerra de bombarderos capaces de volar sin escalas a lo largo de miles de millas y a aviones transcontinentales y transoceánicos de posguerra. Desde 1903 hemos visto rangos de aviones ir de pies a sin parar dando vueltas por el globo y ¡las resistencias van de minutos a días!

6.1 Uso y peso del combustible

Al estudiar el rango y la resistencia debemos, por primera vez en este curso, considerar el uso de combustible. En los aviones de Curtiss y los Wrights, no era raro que el motor dejara de sufrir problemas mecánicos o sobrecalentamiento antes de que se acabara el combustible. En los aviones actuales, el alcance y la resistencia dependen de la cantidad de combustible a bordo. Cuando la última gota de combustible se ha ido el avión ha alcanzado su límite de alcance y resistencia. Uno podría, por supuesto, incluir el alcance de planeamiento y la resistencia después de que el avión se quede sin combustible, ¡pero una aerolínea que operara de esa manera atraería a pocos pasajeros!

El uso de combustible depende del diseño del motor, los ajustes del acelerador, la altitud y una serie de otros factores. Sin embargo, no es el propósito de este texto estudiar la eficiencia del combustible del motor o el uso del acelerador por parte del piloto. Supondremos que se nos da un motor con ciertas especificaciones de eficiencia y uso de combustible y que la configuración del acelerador es la especificada en el manual o manual de la aeronave para un rango óptimo o resistencia a la altitud elegida. Se supone que el alumno tomará un curso separado sobre propulsión para estudiar los orígenes de las figuras utilizadas aquí para estos parámetros.

Nuestra principal preocupación en el uso de combustible será el cambio en el peso de la aeronave con el tiempo. Muchas de nuestras ecuaciones de rendimiento utilizadas en capítulos anteriores incluyen el peso de la aeronave. En esos capítulos tratamos el peso como una constante. El peso es, en realidad, constante sólo para el planeador o velero. Para otras aeronaves el peso siempre va cambiando, siempre disminuyendo a medida que se quema el combustible. Esto significa que el rendimiento aerodinámico del avión cambia durante el vuelo. Esto, sin embargo, no niega el valor de los métodos utilizados anteriormente para estudiar crucero y escalar. Esos cálculos normalmente se realizarán utilizando el peso bruto máximo del avión, lo que conducirá a un análisis conservador o “peor de los casos” de esos parámetros de rendimiento. También podemos utilizar los métodos desarrollados anteriormente para observar las capacidades “instantáneas” de la aeronave en un peso dado, dándonos cuenta de que en un momento posterior en vuelo y a un peso menor, el rendimiento puede ser diferente.

Al considerar el rango y la resistencia es imperativo que consideremos el peso como una variable, cambiando del peso bruto máximo al despegar a un peso del tanque de combustible vacío al final del vuelo. Para ello abordaremos el uso de combustible en términos del peso del combustible (a diferencia del volumen de combustible, en galones, que normalmente usamos para automóviles). Cuando nuestra preocupación es la resistencia nos interesa el cambio de peso del combustible por unidad de tiempo

\[\dfrac{dW_f}{dt}\]

y, cuando el alcance es la preocupación queremos saber cómo disminuye el peso del combustible con la distancia recorrida.

\[\dfrac{dW_f}{dS}\]

A los fabricantes de motores de aviones les gusta especificar el uso de combustible del motor en términos de consumo específico de combustible Para los motores a reacción esto se convierte en un consumo de combustible específico de empuje y para los aviones de apoyo, un consumo de combustible específico de potencia Dado que el empuje y el poder traen diferentes unidades a las ecuaciones debemos considerar los dos casos por separado.

6.2 Rango y Resistencia: Jet

Hablamos de la potencia del motor de un motor a reacción en términos de empuje; por lo tanto, hablamos del uso de combustible del motor a reacción en términos de un consumo de combustible específico de empuje, C _t. C _t es la masa de combustible consumida por unidad de tiempo por unidad de empuje. La unidad de tiempo debe ser de segundos y la unidad de empuje debe estar en libras o Newtons de empuje.

[C _t] = (sl/seg) /lb _empuje, o = (kg/seg) /N _empuje

Lo anterior es la definición _adecuada del consumo de combustible específico de empuje, sin embargo, en realidad no es exactamente lo que necesitamos para nuestros cálculos. Preferiríamos una definición basada en el peso del combustible consumido en lugar de la masa. Así definiremos un peso específico de consumo de combustible, _t, como el peso del combustible utilizado por unidad de tiempo por unidad de empuje. Esto da unidades de (tiempo) ^-1.

\[\left[\gamma_{\mathrm{t}}=\mathrm{gC}_{\mathrm{t}}\right]=\left(\mathrm{lb}_{\text {fuel }} / \mathrm{sec}\right) / \mathrm{lb}_{\text {thrust }}, \text { or }=\left(\mathrm{N}_{\text {fuel }} / \mathrm{sec}\right) / \mathrm{N}_{\text {thrust }}=(\mathrm{sec})^{-1}\]

El lector debe ser consciente de que muchos textos de rendimiento de aeronaves y textos de propulsión son muy vagos con respecto a las unidades de consumo específico de combustible. Algunos incluso lo definen en términos de masa y le dan unidades de 1/seg., haciéndolo dimensionalmente incorrecto. Parte de la confusión, particularmente en los textos de propulsión estadounidenses más antiguos, radica en el uso de la libra de masa como unidad de masa. Esto da una combinación de libras-masa dividida por libras‑fuerza, que, en realidad, da sec ²/ft. La situación se complica entonces aún más por el autor aparentemente lanzando un término llamado g _c que se supone que resuelve el problema lb _m /lb _f. En cualquier caso es muy importante que el ingeniero que utiliza un consumo específico de combustible considere cuidadosamente las unidades involucradas antes de comenzar la solución de un problema de rango o resistencia. Un peso especificado correctamente el consumo de combustible específico tendrá unidades de sec ^-1 y lo hará sin el uso de nada llamado g _c.

Cabe agregar que también se podría encontrar un consumo específico de combustible que se ha calculado utilizando la masa de combustible (kg) y el empuje en kilogramos, una unidad no SI que se utiliza en gran parte del mundo (prácticamente nadie en el mundo sabe qué es un Newton o cómo usarlo). Si esto se hace el valor numérico debe ser el mismo que el obtenido utilizando la definición de consumo de combustible específico de peso anterior.

Algunas fuentes de datos específicos de consumo de combustible utilizan unidades de (horas) ^-1 ya que la hora es una unidad de tiempo más conveniente. El uso de segundos es, sin embargo, correcto en cualquier sistema de unidades estándar y el estudiante puede ser bien aconsejado convertir horas en segundos antes de comenzar el cálculo aunque esto finalmente resultará en el cálculo de la resistencia en segundos, dando números bastante grandes para las respuestas.

Para encontrar resistencia queremos la tasa de cambio de peso de combustible (W _f) por unidad de tiempo que se puede escribir en términos del consumo de combustible específico de empuje

\[\mathrm{dW}_{\mathrm{f}} / \mathrm{dt}=\gamma_{\mathrm{t}} \mathrm{T}\]

Y, en vuelo recto y nivelado donde el empuje es igual a arrastre

\[\mathrm{d} \mathrm{W}_{\mathrm{f}} / \mathrm{dt}=\gamma_{\mathrm{t}} \mathrm{D}\]

Para una máxima resistencia queremos minimizar el término anterior. Esto muestra claramente que para una máxima resistencia el avión jet debe ser volado en condiciones mínimas de arrastre. Veremos cómo encontrar esa resistencia después de echar un breve vistazo al rango.

Para encontrar el rango de vuelo debemos mirar la tasa de cambio del peso del combustible con la distancia de vuelo. Podríamos detenernos un poco en este punto para darnos cuenta de que esto puede ser más complicado que la resistencia porque el alcance dependerá más que simplemente del rendimiento aerodinámico del avión. También requerirá consideración de la velocidad del viento. ¡Un avión puede volar para siempre a una velocidad de 100 mph en un viento en contra de 100 mph y aún así tener un alcance de cero! Por ahora, sin embargo, dejaremos de lado esas preocupaciones y miraremos las matemáticas simples con las que comenzamos a considerar el problema. Analizamos arriba la tasa de cambio de peso con el tiempo. Podemos combinar esto con el cambio de distancia con tiempo (velocidad) para obtener la tasa de cambio de peso con distancia.

\[\mathrm{dW}_{\mathrm{f}} / \mathrm{dS}=\left(\mathrm{dW}_{\mathrm{f}} / \mathrm{dt}\right) /(\mathrm{dS} / \mathrm{dt})=\gamma_{\mathrm{t}}(\mathrm{T} / \mathrm{V})=\gamma_{\mathrm{t}}(\mathrm{D} / \mathrm{V})\]

Tenga en cuenta que todavía asumimos D = T o vuelo recto y nivelado.

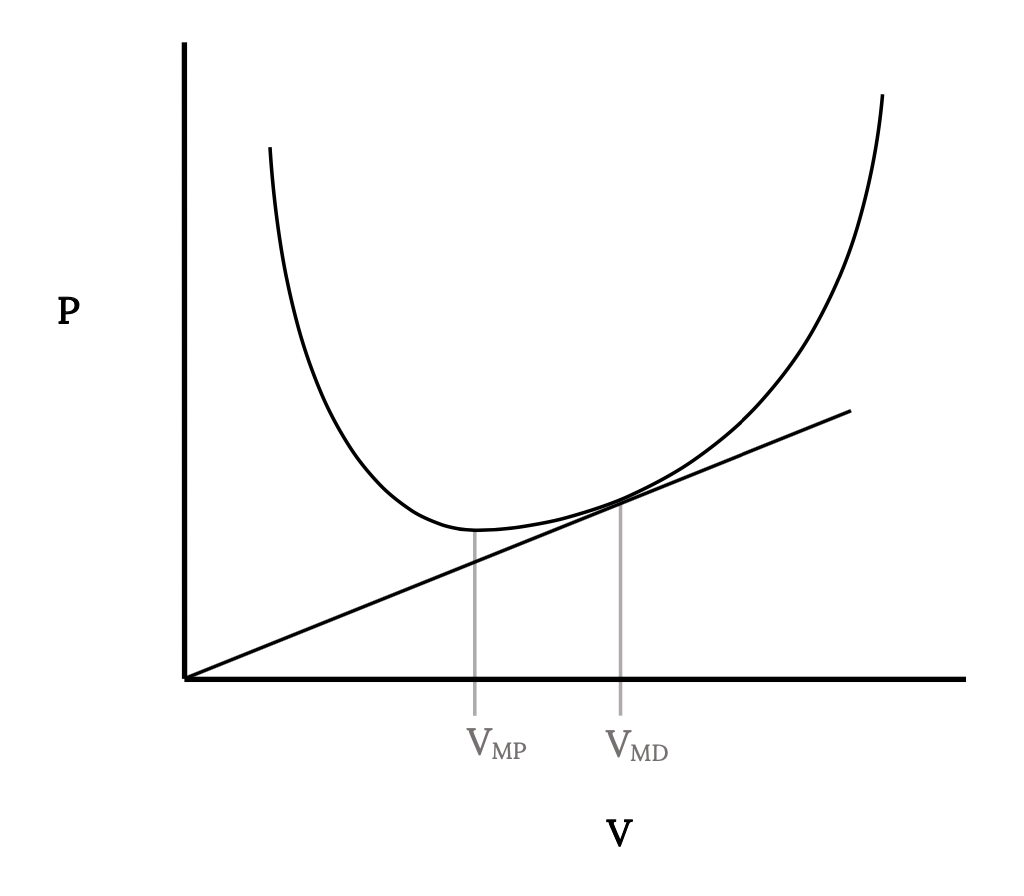
De lo anterior es obvio que el rango máximo ocurrirá cuando el arrastre dividido por velocidad (D/V) sea mínimo. Esta no es una condición que hayamos estudiado anteriormente pero podemos hacernos una idea de dónde ocurre esto observando la trama de arrastre versus velocidad para una aeronave.

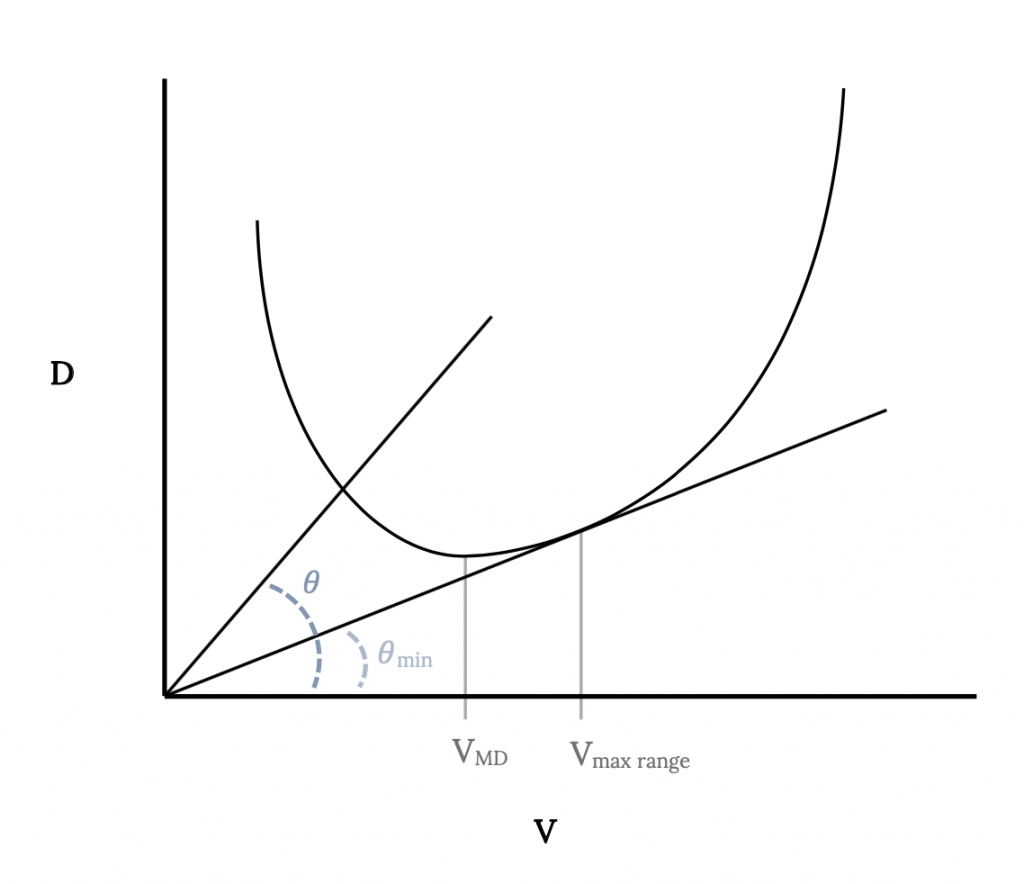
Una gráfica muestra la tapa de arrastre D en el eje vertical, mientras que la tapa de velocidad V es el eje horizontal. La curva de arrastre se asemeja a una parábola, con el lado derecho ligeramente aplanado. Una línea arbitraria se dibuja desde el origen hacia la curva de arrastre en un ángulo theta por encima del eje horizontal. Se dibuja una segunda línea tangente a la curva en un ángulo correspondiente theta sub min, intersecando la línea a la velocidad para el rango máximo, cap V rango sub max. El punto más bajo en la curva de arrastre se produce en la tapa V sub tapa M tapa D. — Figura 6.1: Encontrar la velocidad para el rango máximo

En esta gráfica una línea trazada desde el origen para intersectar la curva de arrastre en cualquier punto tiene una tangente igual al arrastre en el punto de intersección dividido por la velocidad en ese punto. El valor mínimo posible de D/V para la aeronave representada por la curva de arrastre debe encontrarse entonces cuando la línea es tangente a la curva de arrastre. Este punto dará la velocidad para el rango máximo. Tenga en cuenta que es una velocidad mayor que la de arrastre mínimo (que, a su vez, fue mayor que la velocidad para la potencia mínima).

En lo anterior hemos encontrado las condiciones necesarias para lograr el máximo alcance y resistencia para un avión a reacción. Aún no hemos encontrado ecuaciones para el rango real o la resistencia. Para encontrarlos necesitamos volver a los diferenciales de tiempo y distancia e integrarlos. Por el tiempo tenemos

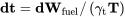
$dt=DWFuel/ (γTT)$

Ahora deseamos poner las ecuaciones en una forma que incluya el peso de la aeronave en lugar del peso del combustible. Dado que el cambio de peso de la aeronave en vuelo es igual y opuesto al peso del combustible consumido

dW = — _combustible dW

tenemos

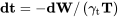
$dt=−dw/ (γTT)$

Por último, integrándose a lo largo del tiempo para encontrar la resistencia da

$E = −w1w2dWγtt$

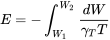
De manera similar el rango se encuentra desde el diferencial de distancia

$DS=−VdW/ (γTT)$

$R=−w1W2VdWγTT$

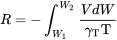
En las ecuaciones anteriores debemos saber cómo varían la velocidad de la aeronave, el empuje y el consumo específico de combustible con el peso de la aeronave. En este punto necesitamos hacer algunas suposiciones sobre la forma en que se va a realizar el vuelo. Esto a veces se llama el “horario de vuelo”.

6.3 Soluciones aproximadas para rango y resistencia para un jet

La primera suposición que se debe hacer al encontrar ecuaciones de rango y resistencia es que el vuelo será esencialmente recto y nivelado. Para darnos algún margen de maniobra llamaremos a este vuelo “cuasi-nivelado”, siendo nuestro deseo meramente utilizar las relaciones L = W. T = D.

T = D = W (D/L) = W (C _D /C _L),

y también podemos usar

$v=2WρSCL$

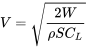
Sustituyendo estos en las relaciones de rango y resistencia anteriores dan

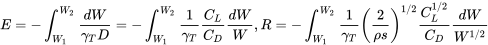
$E=−w1W2dWγtd=−w1W21γtCLCDDWw, R=−w1W21γT (2ρs) 1/2CL1/2CDDWw1/2$

En este punto necesitamos hacer algunas suposiciones adicionales sobre el horario de vuelo para simplificar la integración de estas ecuaciones. Por ejemplo, en la ecuación de resistencia, si asumimos que el vuelo se realiza en constante ángulo de ataque, estamos asumiendo

que los coeficientes de elevación y arrastre son constantes para todo el vuelo. Si también asumimos que el consumo específico de combustible es constante para el vuelo la única variable que queda en la integral es el peso mismo y la integral se convierte en:

$E=−1γTCLCDW1W2DWW=1γTCLcDLN (W1W2) (constα)$

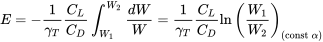
La integral de rango contiene una variable adicional, la densidad de la atmósfera. Todavía es posible hacer un par de combinaciones de suposiciones que resultarán en una integración simple y condiciones de vuelo realistas. El primer caso será asumir crucero tanto a altitud constante como a ángulo de ataque constante dando tanto densidad como los coeficientes de sustentación y arrastre como constantes en la integración.

$R=22γTρSCL1/2CD (W1−W2) (constαconst V)$

Un segundo caso simple combina los supuestos de ángulo de ataque constante y velocidad constante, que pueden usarse con la forma anterior de la ecuación de rango.

$r=−w1w2vdwγtt=−w1w2vγtCLcddww$

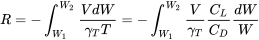
dando

$r=VγTCLcDLN (W1W2) (constαconst V)$

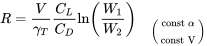
Tenga en cuenta que la última ecuación anterior es simplemente la ecuación de resistencia multiplicada por la velocidad. Esto no debería sorprender ya que este es el caso donde la velocidad es constante.

En las ecuaciones finales anteriores para rango y resistencia debemos señalar que si se utilizan unidades estándar con consumos específicos de combustible en seg. ^-1, el rango se dará en pies o metros y la resistencia en segundos. Puede que nos resulte más fácil determinar el grado en que nuestras respuestas son realistas si convertimos estas respuestas a millas o kilómetros y horas.

Al encontrar las ecuaciones anteriores para rango y resistencia, solo hemos mirado casos especiales que resultarían en integraciones simples. Si conocemos horarios de vuelo más complicados podemos determinar las relaciones funcionales entre los coeficientes de elevación y arrastre, velocidad, densidad, etc. y la pérdida de peso durante el vuelo e insertarlos en las integrales originales para resolver el alcance y la resistencia. Sin embargo, los casos anteriores son muy cercanos a las condiciones reales de los cruceros operativos para aviones de largo alcance y probablemente serán suficientes para un estudio introductorio del rendimiento de las aeronaves. Echemos un vistazo a esos casos simples.

Ambos casos de rango incluyeron nuestra suposición de resistencia de ángulo de ataque constante y consumo específico de combustible. El primer caso combinó estos supuestos con especificación de altitud constante. Este parece ser el caso más simple para volar realmente pero para ver lo que realmente significa necesitamos volver a la relación de velocidad de vuelo recta y nivelada

V = [2W/ (ρ SC _L)] ^1/2

o VW ^1/2, cuando ρ y d C _L son ambas constantes.

Si tanto la altitud (densidad) como el ángulo de ataque (coeficiente de sustentación) son constantes, es obvio que la velocidad debe cambiar a medida que cambia el peso. Es decir, para este horario de vuelo a medida que se quema combustible y disminuye el peso de la aeronave, la velocidad de vuelo debe disminuir en proporción a la raíz cuadrada del peso.

El otro caso, velocidad constante combinada con ángulo de ataque constante, se ve a partir de la relación de velocidad anterior para requerir que la densidad disminuya en proporción al peso.

W/ ρ = const. cuando V y C _L son constantes.

Esto significa que a medida que la aeronave quema combustible, la aeronave se moverá lentamente a altitudes más altas donde la densidad es menor. Esto se conoce comúnmente como el horario de vuelo a la deriva. Esto en realidad es muy similar a la forma en que los aviones comerciales vuelan rutas de larga distancia. Aquellos de ustedes que hayan estado en esos vuelos recordarán al piloto anunciando que “ahora estamos de crucero a 35 mil pies y subiremos a 39 mil pies después de cruzar el Mississippi” o algún plan de este tipo. Si bien la FAA no permitirá que los aviones simplemente se “desplacen” mientras vuelan de costa a costa, permitirán horarios que se aproximen incrementalmente a la técnica de deriva.

Cabe señalar que las dos ecuaciones de rango anteriores darán dos respuestas diferentes para la misma cantidad de combustible. También tenga en cuenta que las ecuaciones se basan únicamente en la parte de crucero del vuelo. Un vuelo real incluirá despegue, ascenso a la altitud del crucero, descenso y aterrizaje además del crucero. También se debe tener en cuenta el combustible de reserva para manejar situaciones de emergencia y “retenciones” impuestas por los controladores de tránsito aéreo.

La mayor suposición utilizada en todas las integraciones anteriores es la de ángulo de ataque constante. Si bien esto se ajusta a nuestras condiciones para casos óptimos como máxima resistencia

que ocurre en la relación máxima de sustentación a arrastre (arrastre mínimo), puede que no se ajuste muy bien al vuelo real. Si bien el piloto puede monitorear fácilmente su velocidad aérea y altitud, el ángulo de ataque del avión no es tan fácil de monitorear y controlar directamente.

Las ecuaciones anteriores para rango y resistencia son válidas para cualquier condición de vuelo que se encuentre dentro de los supuestos hechos en su derivación. Si tenemos un Boeing 747 volando a un ángulo de ataque de ocho grados y una velocidad de 250 millas por hora estas ecuaciones pueden ser utilizadas para encontrar el alcance y la resistencia aunque esto obviamente no es una velocidad y ángulo de ataque óptimos. Si queremos determinar el rango óptimo o resistencia debemos usar los valores de coeficiente de sustentación y arrastre y la velocidad que antes encontramos que era necesaria para estos óptimos.

Anteriormente encontramos que para una máxima resistencia la aeronave necesita volar en condiciones mínimas de arrastre. Nuestra ecuación de resistencia real lo confirma, mostrando la resistencia como una función de la relación del coeficiente de elevación a resistencia, que será un máximo si la resistencia es mínima.

También encontramos que el rango sería óptimo si la resistencia dividida por velocidad fuera mínima. La correlación entre esta condición y las ecuaciones de rango derivadas no es tan obvia como la de arrastre mínimo con la ecuación de resistencia. Usando las relaciones de fuerza de vuelo rectas y niveladas que pueden ser manipuladas para mostrar

D = W [D/L] = W [C _D /C _L]

la cantidad V/D se puede escribir

V/D = [V/ W] [C _L /C _D].

Ahora usando la relación de velocidad para vuelo recto y nivelado

$V= [2W/ (ρSCL)] 1/2$

encontramos

$V/D= [2W/ρS] 1/2 (1/W) (CL1/2/CD)$

Por lo tanto, encontramos que el rango máximo ocurre cuando, para un peso y altitud dados

C _L ^1/2 /C _D es un máximo.

Si asumimos un arrastre parabólico polar con constante C _D0 y K podemos escribir

C _L ^1/2 /C _D = C _L ^1/2/[C _D0 + KC _L ²]

Para encontrar cuando esta combinación de términos está en un máximo podemos tomar su derivada con respecto a su variable (C _L) y establecerla igual a cero.

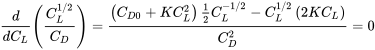
$DDCl (CL1/2CD) = (CD0+KCL2) 12CL−1/2-CL1/2 (2KCL) CD2=0$

Resolver esto da

½ (C _D0 + KC _L ²) C _L ^1/2 — (2KC _L ² )/C _L ^1/2 = 0

C _D0 + KC _L ² -4KC _L ² = 0

entonces

C _D0 = 3KC _L ²

y, finalmente

C _L = [C _D0/3K] ^1/ ².

Por lo tanto, para un rango máximo

$CLMАХR=CD03K.$

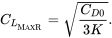
El uso de esto en el polar de arrastre da el valor del coeficiente de arrastre para el rango máximo

C _Dmax _R = C _D0 + KC _LMaxr ² = C _D0 + KC _D0 /(3K) = (4/ 3) C _D ₀.

Estas se conocen como las condiciones para el rango máximo “instantáneo”. Se utiliza el término instantáneo porque los cálculos son para un peso dado y sabemos que el peso está cambiando durante el vuelo. Es decir, en cualquier punto durante el vuelo, en el peso y altitud en ese punto, los coeficientes de sustentación y arrastre encontrados arriba darán el mejor alcance.

6.4 Rango y Resistencia: Prop

Ahora veremos el alcance y la resistencia de los aviones impulsados por hélice en los que el rendimiento del motor se expresa normalmente en términos de potencia en lugar de empuje. Se realiza un examen de alcance y resistencia para aeronaves que tienen un rendimiento medido en términos de potencia (aviones de hélice) definiendo un consumo de combustible específico de potencia similar al consumo de combustible específico de empuje utilizado para los jets. El consumo de combustible específico de potencia se define como la masa de combustible consumida por unidad de tiempo por unidad de potencia de eje. Las unidades son babosas por unidad de potencia por segundo en el sistema inglés o kilogramo por unidad de potencia por segundo en unidades SI.

[C _p] = sl/(poder-seg) o kg/ (poder-seg)

Las unidades de potencia utilizadas son caballos de fuerza en el sistema inglés y vatios en unidades SI.

Tal como lo hicimos en el caso del jet (empuje), a menudo encontraremos una definición alternativa de consumo específico de combustible dada en términos del peso del combustible consumido en lugar de la masa.

$γP=GCP [lbcombustible/hp seg. ornCombustible/vatio seg.]$

Si bien la unidad de tiempo adecuada son segundos, a menudo encontraremos dichos datos dados para un motor en términos de horas. Desarrollaremos nuestras ecuaciones en términos de las unidades fundamentales (segundos por tiempo) y, como en el caso jet, asumiremos un vuelo “cuasi-nivel” que tiene

P _avail = P _req = DV

Al tratar con los motores de propulsión debemos considerar la eficiencia propulsora, η _p, que relaciona la potencia del eje, P _s, proveniente del propio motor con la potencia efectivamente utilizada por el puntal para transferir impulso al aire.

$Pavail=dv=ηpps$

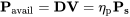
En cuanto al jet, para encontrar resistencia debemos considerar

$dwf/dt=γPPS=γPDV/ηP$

y para rango están interesados en

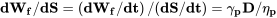
$DwF/ds= (DwF/dt)/(dS/dt) =γPd/ηP$

De las ecuaciones anteriores es obvio que, para un determinado consumo y eficiencia de combustible específicos, la tasa de uso de combustible es mínima (la resistencia instantánea es máxima) cuando la potencia requerida (DV) es mínima. También es obvio que el uso de combustible por cantidad de distancia recorrida es mínimo (rango instantáneo es máximo) cuando el arrastre es mínimo.

Así que nuevamente nos encontramos con nuestros viejos amigos, la potencia mínima requerida y el arrastre mínimo como condiciones necesarias para un vuelo óptimo. Ya sabemos cómo encontrarlos gráficamente a partir de gráficas de potencia versus velocidad como se muestra a continuación. Esta determinación gráfica de potencia mínima y velocidades mínimas de arrastre es válida para cualquier polar de arrastre, aunque no sea parabólico.

Una gráfica muestra la tapa de potencia P en el eje vertical, mientras que la tapa de velocidad V es el eje horizontal. Se muestra una curva de potencia parabólica similar a la curva de arrastre en la figura anterior. Se dibuja una línea tangente a la curva, que se cruza a la velocidad para un arrastre mínimo, cap V sub cap M cap D. La potencia mínima ocurre en cap V sub cap M cap P, en la parte inferior de la curva de potencia. — Figura 6.2: Velocidades para Potencia Mínima y Arrastre

En este punto debemos hacer una pausa y decir: “¡Oye, espera solo un minuto! Fue solo un par de páginas atrás que dijiste que la máxima resistencia se producía en condiciones mínimas de arrastre. Ahora dices que es el rango máximo que obtengo en condiciones mínimas de arrastre. ¡Decídete, por el amor de Dios!”

El problema es que en un caso estamos hablando de jets y el otro, aviones de apoyo. Esto significa que debemos tener mucho cuidado para ver con qué tipo de avión estamos tratando antes de comenzar cualquier cálculo. Es muy fácil meterse en una gran prisa y mezclar los dos casos (¡especialmente en el fragor de la batalla en una prueba o examen!).

Ahora, como hicimos para el jet, podemos desarrollar integrales para determinar el alcance o la resistencia para cualquier situación de vuelo. Para la resistencia tenemos

$E=t1t2dt=−w1w2ηpdwγPDV$

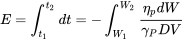
y para la gama

$r=s1s2ds=−w1w2ηpdwγPD$

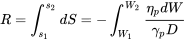
6.5 Soluciones aproximadas para alcance y resistencia para una aeronave de apoyo

Una vez más asumiremos el vuelo “cuasi-nivel” y manipularemos los términos en nuestras relaciones de equilibrio de fuerza para dar

\[D = W\left[\dfrac{D}{L}\right] = W\left[\dfrac{C_D}{C_L}\right]\]

Esto hace que la resistencia sea integral

\[\mathrm{E}=-\int_{W_{1}}^{\mathrm{W} 2} \frac{\eta_{\mathrm{p}}}{\gamma_{\mathrm{p}}} \frac{1}{\mathrm{~V}} \frac{\mathrm{C}_{\mathrm{L}}}{\mathrm{C}_{\mathrm{D}}} \frac{\mathrm{d} \mathrm{W}}{\mathrm{W}}\]

Uso de la relación de velocidad recta y nivelada

\[\mathrm{V}=\left[2 \mathrm{~W} /\left(\rho \mathrm{SC}_{\mathrm{L}}\right)\right]^{1 / 2}\]

obtenemos

\[\mathbf{E}=-\int_{\mathbf{W} 1}^{\mathrm{W} 2} \frac{\eta_{\mathrm{p}}}{\gamma_{\mathrm{p}}}[\rho \mathrm{S} / 2]^{1 / 2} \frac{\mathrm{C}_{\mathrm{L}}^{3 / 2}}{\mathrm{C}_{\mathrm{D}}} \frac{\mathrm{dW}}{\mathrm{W}^{3 / 2}}\]

La integral de gama se puede escribir de manera similar a

\[R=-\int_{W_{1}}^{W_{2}} \frac{\eta_{P}}{\gamma_{P}} \frac{C_{L}}{C_{D}} \frac{d W}{W}\]

Ahora necesitamos considerar los mismos horarios de vuelo examinados en el caso jet. El ángulo constante de vuelo de ataque dará constantes coeficientes de sustentación y arrastre y la altitud constante dará densidad constante. También asumiremos un consumo constante de combustible específico.

Para el rango solo necesitamos usar la suposición de ángulo de ataque constante para dar una integral simple. El rango resultante es

\[R=\frac{\eta_{P}}{\gamma_{P}} \frac{C_{L}}{C_{D}} \ln \left(\frac{W_{1}}{W_{2}}\right), \quad(\text { const } \alpha)\]

Para la resistencia consideraremos dos casos. El primero mantiene constantes tanto la altitud como el ángulo de ataque, dando

\[E=-\frac{\eta_{P}}{\gamma_{P}} \sqrt{\frac{\rho S}{2}} \frac{C_{L}^{3 / 2}}{C_{D}} \int_{W_{1}}^{W_{2}} \frac{d W}{W^{3 / 2}}\]

que se integra a

\ [E=\ frac {\ eta_ {P}} {\ gamma_ {P}}\ sqrt {2\ rho S}\ frac {C_ {L} ^ {3/2}} {C_ {D}}\ izquierda (\ frac {1} {\ sqrt {W_ {2}} -\ frac {1} {\ sqrt {W_ {1}}}\ derecha),\ left (\ begin {array} {l}
\ text {const}\ alpha\
\ text {const}\ rho
\ end {array}\ right)\]

El segundo caso tiene ángulo de ataque y constante de velocidad

\[E=-\frac{\eta_{P}}{\gamma_{P}} \frac{1}{V} \frac{C_{L}}{C_{D}} \int_{W_{1}}^{W_{2}} \frac{d W}{W}\]

\ [E=\ frac {\ eta_ {P}} {\ gamma_ {P}}\ frac {1} {V}\ frac {C_ {L}} {C_ {D}}\ ln\ izquierda (\ frac {W_ {1}} {W_ {2}}\ derecha),\ quad\ izquierda (\ begin {array} {l}
\ text {const}\ alfa\
\ texto {const} V
\ end {array}\ derecha)\]

Este es el horario de vuelo “drift up”.

6.6 Efectos de viento

Las ecuaciones de rango y resistencia anteriores para aviones a reacción o propulsión se derivaron asumiendo que no había vientos atmosféricos. Las velocidades en las ecuaciones son las velocidades del aire, no las velocidades sobre el suelo. Si hay viento la velocidad del aire es, por supuesto, no igual a la velocidad sobre el suelo.

Los cálculos de resistencia no se ven alterados por la presencia de un viento atmosférico. Si nuestra preocupación es cuánto tiempo puede permanecer el avión en el aire a una velocidad aerodinámica y altitud dadas y no nos importa especialmente si está progresando sobre el suelo, no necesitamos preocuparnos por los vientos. Estamos haciendo cálculos de resistencia basados únicamente en el comportamiento aerodinámico del avión a una velocidad y altitud dadas en una masa de aire.

El rango está relacionado con la velocidad a través del suelo en lugar de la velocidad del aire; por lo tanto, si hay viento, nuestros resultados de la ecuación de rango deben ser reevaluados para tener en cuenta el viento. La lógica de esto es simple: un viento en contra ralentizará el progreso sobre el suelo y reducirá el alcance mientras que un viento de cola aumentará el alcance. Lo que no es tan obvio es cómo corregir los cálculos para dar cuenta de este viento. Dado que nuestra preocupación habitual es encontrar el alcance máximo, examinaremos la corrección de los efectos del viento solo para esta situación óptima.

Se encontró que el rango máximo para un chorro se producía cuando D/V era mínimo mientras que, para un puntal, el rango máximo ocurrió en condiciones mínimas de arrastre. Las velocidades para ambos casos se pueden determinar gráficamente encontrando el punto de tangencia para una línea trazada desde el origen de velocidad cero en la curva de arrastre versus velocidad en la caja de chorro o la curva de potencia requerida frente a velocidad para el plano de apoyo. Podemos usar una extensión de este enfoque gráfico para encontrar la velocidad para el mejor rango con un viento de cabeza o un viento de cola.

El primer paso importante para determinar el rango óptimo en presencia de un viento atmosférico es encontrar una nueva velocidad aérea para el mejor rango con un viento. Esta nueva velocidad se utilizará entonces para calcular un nuevo valor del rango óptimo. El nuevo valor de la velocidad aérea de mejor rango se encuentra como se ilustra en las siguientes figuras. La primera tarea es dibujar una gráfica convencional de arrastre versus velocidad (para un chorro) o potencia requerida versus velocidad (para un puntal). A esta parcela se le agrega un nuevo origen, desplazado a la izquierda por el valor de un viento de cola o a la derecha por la magnitud del viento de cola. Luego se dibuja una línea desde el origen desplazado, tangente a la curva de arrastre o potencia y el punto de tangencia localiza la nueva velocidad para un rango óptimo con un viento. La magnitud de esta nueva velocidad de rango óptimo se lee con respecto al origen original (no al origen desplazado). Esta velocidad es una velocidad aérea, no una velocidad de avance.

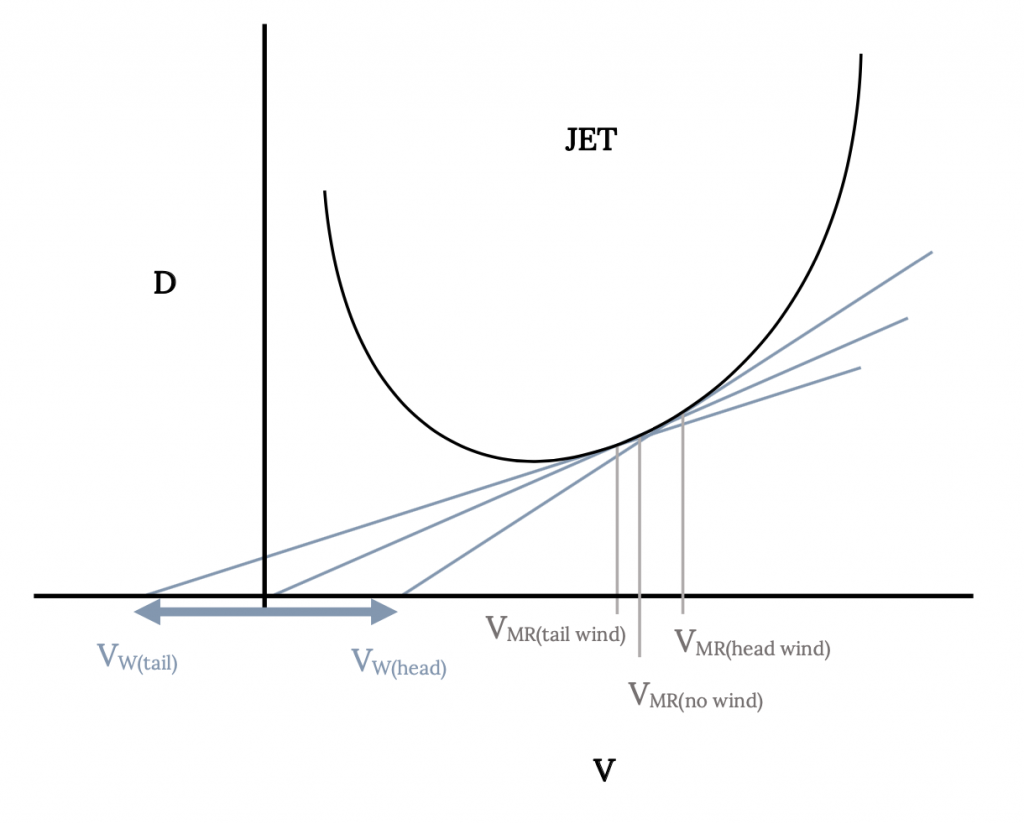
La misma gráfica cap D versus cap V para un chorro se muestra como antes, pero ahora con tres líneas tangentes. La línea original que interseca la curva de arrastre en la tapa V sub cap M cap R está presente. Se muestra una segunda línea para un viento de cola, que comienza con un valor negativo de cap V correspondiente a cap V sub w tail, lo que hace que se cruce con la curva de arrastre en un valor de cap V inferior, etiquetado cap V sub cap M cap R tailwind. Se muestra una tercera línea para un viento de cabeza, que comienza con un valor positivo de cap V correspondiente a cap V sub w head, lo que hace que se cruce con la curva de arrastre a un valor de cap V más alto, etiquetado cap V sub cap M cap R viento en contra. — Figura 6.3: Velocidad para el mejor rango con viento (Jet)

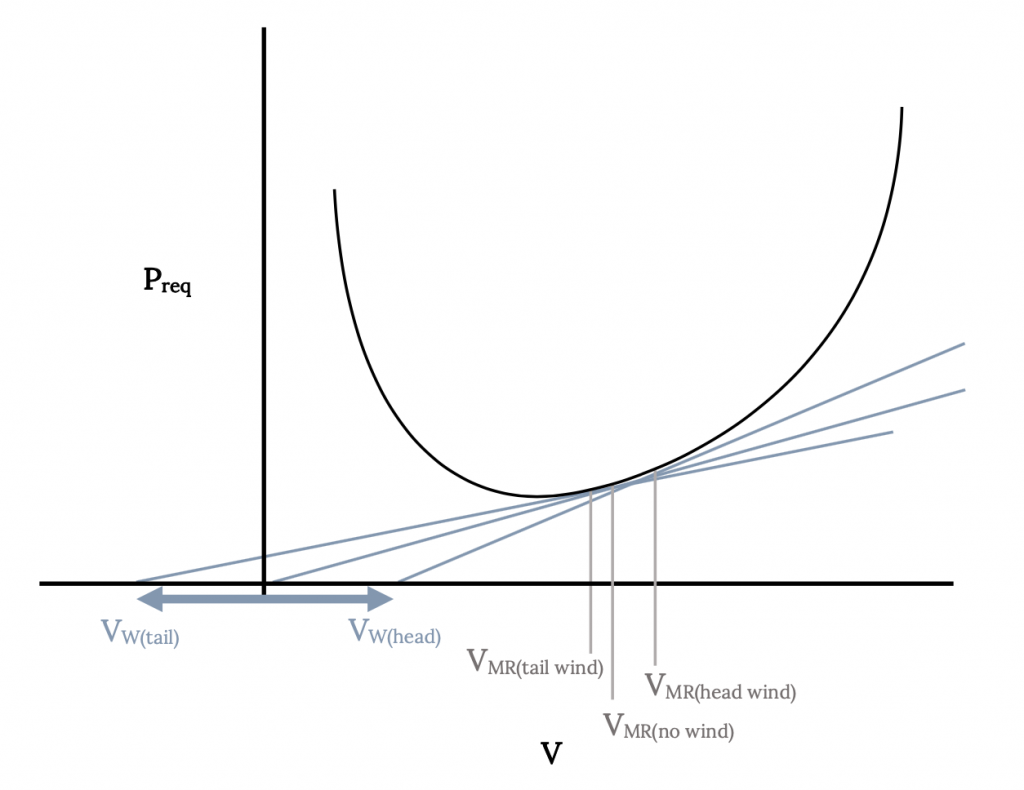
Se muestra una gráfica que vuelve a representar la figura anterior, pero con la potencia requerida cap P sub req en el eje vertical en lugar de la tapa de arrastre D. Se muestra el mismo fenómeno, con una tapa de cambio de viento de cola V sub cap M cap R viento de cola a un valor más bajo, y una tapa de cambio de viento en contra V sub cap M cap R viento en contra a un valor más alto. — Figura 6.4: Velocidad para el mejor rango con viento (Prop)

Esta nueva velocidad de rango óptimo se utiliza entonces para encontrar un nuevo valor de rango a partir de las mismas ecuaciones desarrolladas anteriormente. Usando la nueva velocidad, primero se calculan nuevos valores de los coeficientes de sustentación y arrastre y estos nuevos coeficientes y velocidad se utilizan para encontrar el rango óptimo con el viento. A esta nueva gama hay que añadir otra gama que resulta puramente del tiempo de exposición (resistencia) de la aeronave al viento. Esta resistencia también se encuentra utilizando la velocidad de rango óptimo recién encontrada y los coeficientes asociados. El rango final corregido para el rango máximo en un viento es

R _con _viento = R _Corregido + V _w E _Corregido para un viento de cola

R _con _viento = R _Corregido — V _w E _Corregido para viento en contra

6.7 Deje que el comprador tenga cuidado

A los fabricantes de aviones, como los de los automóviles y otros productos, les gusta hacer todo lo posible para que su producto se vea bien y a veces esperan que el comprador no mire demasiado de cerca las contradicciones en sus especificaciones y publicidad. Se puede anunciar que un automóvil tiene asientos para cinco personas, una clasificación de economía de combustible de la EPA de 38 mpg, la capacidad de recorrer 542 millas en un solo tanque de gasolina y una velocidad máxima de 120 millas por hora. La mayoría de nosotros, sin embargo, sabemos no esperar que ese auto vaya 542 millas en un solo tanque de gasolina mientras transporta a 5 personas a una velocidad de 120 mph! Aquellos que creen que lo hará probablemente también serían lo suficientemente tontos como para pagar el precio de la pegatina.

¿Qué pasa con los aviones? ¿Es este producto de una industria que está regulada a cada paso por la FAA tan sujeta a contradicción en especificaciones como un automóvil?

Veamos algunos ejemplos simples tomados de un Directorio de Flotas de Aeronaves de aviación general de hace unos años. A Cessna 150, el avión de dos lugares más utilizado en el país, cita un alcance de 815 millas náuticas en 32 galones (210 libras) de combustible. El avión tiene un peso vacío (sin piloto, pasajero, equipaje o combustible) de 1104 libras y un peso bruto máximo de despegue de 1600 libras. Esto significa que con los tanques de combustible llenos necesarios para el alcance máximo solo hay una asignación de 286 libras tanto para piloto como para pasajero, ¡apenas suficiente para dos adultos y equipaje! Es por ello que una de las preguntas favoritas de los examinadores de vuelo que se están preparando para un che‑ride de piloto privado en un Cessna 150 involucra el peso y el equilibrio de la aeronave y por qué a veces los pilotos pueden tener que bombear combustible de un avión antes del despegue.

Un Cessna 172, el avión de cuatro lugares más popular del mundo, es un poco mejor que los 150 citados anteriormente. Tiene un peso vacío de 1387 libras y para alcanzar su alcance anunciado de 742 millas cuenta con un tanque de combustible que contiene 288 libras de gasolina. Esto da un peso total para avión y combustible de 1675 libras. El peso bruto máximo de despegue de las 172 es de 2300 libras, dejando 625 libras de subsidio para cuatro pasajeros y sus cosas; ¡un promedio de 156 libras cada uno! Está empezando a parecer que los aviones están diseñados como esos autos de “cuatro lugares” que tienen un asiento trasero lo suficientemente grande como para asentar a dos pequeños caniches!

Con otro producto Cessna, lo mejor de su línea de 4 asientos, el Skylane, las cosas están un poco mejor. Su peso vacío listado de 1707 libras, rango de 979 millas náuticas con 474 libras de combustible y peso bruto máximo de 2950 libras dejan 769 libras para piloto, pasajeros y accesorios (192 libras cada uno). ¡Por fin un avión para gente real!

Para que los ingenuos no tengan la idea de que esto es solo un problema para los pequeños aviones monomotor, veamos un ejemplo más, el Learjet 25C de ocho lugares. Afirma un alcance de 2472 millas, solo el boleto para que la joven y rica magnate de los negocios lo llene con siete de sus amigos más cercanos para una salida transcontinental de fin de semana. La capacidad de combustible listada de 7393 libras, se suma al peso “cero combustible” cotizado de 11,400 libras para dar un avión de 18,793 libras. Entonces, ¿cuánto queda para esos 8 pasajeros? ¡El peso bruto máximo indicado del Learjet 25C es de 15,000 libras! ¡Con un tanque lleno de gasolina el avión está por encima de su peso máximo permitido de despegue! Con un piloto de 160 libras y ningún otro pasajero o carga útil, este avión puede transportar suficiente combustible para un alcance real de aproximadamente 1150 millas, menos de la mitad de lo anunciado. ¿Por qué reclamar un alcance de casi 2500 millas? Bueno, los tanques de combustible son lo suficientemente grandes como para llevar el combustible necesario. ¡Si tan solo el avión pudiera despegar del suelo!

Testos 6

1. Un avión pesa 56,000 libras y tiene un área de ² alas de 900 pies. Su ecuación polar de arrastre viene dada por C _D = 0.016 + 0.04C _L ². El avión tiene un turborreactor con empuje constante a cualquier altitud dada como se muestra a continuación:

Cuadro 6.1: Pregunta 1

altitud (ft)	0	5000	10,000	15,000	20,000	25,000	30,000
empuje (lb)	6420	5810	5200	4590	4000	3360	2700

a. Encuentre el empuje mínimo requerido para el vuelo recto y nivelado y las velocidades reales correspondientes al nivel del mar y a 30,000 pies.

b. encontrar la potencia mínima requerida y las velocidades reales correspondientes al nivel del mar y 30,000 pies.

2. Para los aviones anteriores:

a. trazar empuje y arrastre vs V _e para vuelo recto y nivelado.

Se muestra una gráfica con Drag y Thrust en incrementos de mil libras en el eje vertical, y tope de velocidad V en incrementos de 100 pies por segundo en el eje horizontal. El eje vertical va de 0 a 7 mil, mientras que el eje horizontal va de 0 a 600. — Figura 6.5: Empuje y Arrastre Versus V _e Para Vuelo Recto y Nivel

b. altitud de parcela vs V _emax y V _max para vuelo recto y nivelado.

Figura 6.6: Velocidad máxima (y mínima) para vuelo recto y nivelado versus altitud

c. encontrar la altitud para la máxima velocidad aérea verdadera.

d. encontrar la altitud máxima obtenible.

e. comparar V al mínimo arrastre de la parcela y el cálculo.

f. calcular (L/D) _máx.

Referencias

Figura 6.1: Gris Kindred (2021). “Encontrar la velocidad para el rango máximo”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/6.1-updated

Figura 6.2: Gris Kindred (2021). “Velocidades para Potencia Mínima y Arrastre”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/6.2-updated

Figura 6.3: Gris Kindred (2021). “Velocidad para el Mejor Rango con Viento (Jet).” CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/6.3-updated

Figura 6.4: Gris Kindred (2021). “Velocidad para el Mejor Rango con Viento (Prop.)” CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/6.4-updated

Figura 6.5: Gris Kindred (2021). “Empuje y Arrastre Versus V_e Para Vuelo Recto y Nivel”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/hw-6-part-1

Figura 6.6: Gris Kindred (2021). “Velocidad máxima (y mínima) para vuelo recto y nivelado versus altitud”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/hw-6-part-2

El término “avión” originalmente se refería a un ala, una superficie geométricamente plana destinada a soportar un vehículo en vuelo por el aire. Para 1903 el término se había asociado con todo el vehículo volador. Para la década de 1920 la prensa y las revistas estadounidenses habían cambiado la palabra a “aviones”; sin embargo, todavía es común en Gran Bretaña ver “avión” utilizado en libros y papeles.

<! — pb_fixme —><! — pb_fixme —>

Search

Text Color

Text Size

Margin Size

Font Type

6.7 Deje que el comprador tenga cuidado

Testos 6