1.5: Uso de modelos
- Page ID
- 85976
Capítulo Tabla de Contenidos
- Modelos en General
- Modelos Deterministas
- Ejercicios
Modelos en General
Los ingenieros industriales, y otros ingenieros, a menudo quieren realizar experimentos en sistemas reales, pero tal experimentación puede ser difícil. Si un IE quiere probar un nuevo diseño para un sistema de producción, mover equipos, muebles y oficinas sería difícil y llevaría mucho tiempo. Incluso probar un nuevo procedimiento puede interrumpir el sistema de producción. Por lo tanto, el IE crearía un modelo del sistema, generalmente un modelo matemático.
En la siguiente figura se muestra cómo se utilizan los modelos.
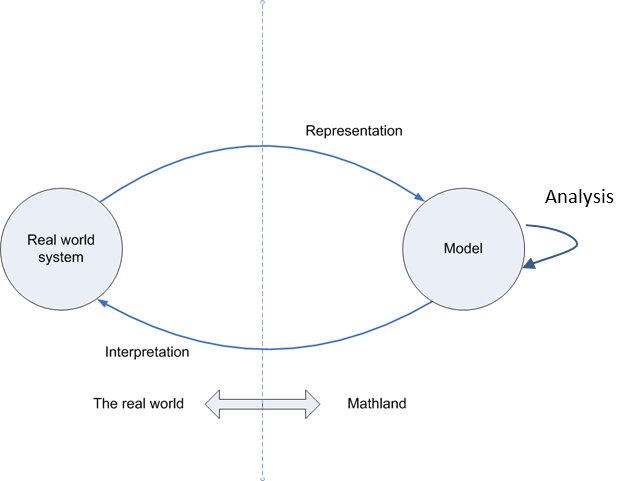
Veamos cada pieza del diagrama. El primer círculo está etiquetado como “sistema del mundo real”. Dibujar una línea alrededor de algún sistema implica decidir qué partes están en su sistema y cuáles están en el entorno. Por ejemplo, para estudiar la llegada y el servicio de clientes a un banco, probablemente incluirías a los cajeros, la ventanilla para subir y el cajero automático, pero no incluirías las carreteras y el sistema de tránsito que la gente usa para llegar al banco.
El segundo círculo está etiquetado como “ modelo” . Algunos tipos de ingenieros utilizan modelos físicos. Por ejemplo, un ingeniero civil podría colocar un modelo a escala de un edificio sobre una mesa temblorosa para predecir cómo responderá el edificio a un terremoto. Los IE tienden a utilizar modelos matemáticos, expresados en ecuaciones o a veces en código de computadora. Por ejemplo, un IE podría utilizar las matemáticas de la teoría de colas para crear un modelo del banco.
La flecha superior etiquetada como “ representación ” nos recuerda que el modelo representa el sistema del mundo real pero solo las partes relevantes del sistema. Nuestro modelo del banco debe incluir información sobre el tiempo entre la llegada de los clientes y el tiempo para atender a cada cliente (ambos tiempos varían de cliente a cliente), pero el modelo no tiene que incluir descripciones de qué color de ropa usan los clientes. Dependiendo del propósito de nuestro modelo, podría incluir información sobre las discapacidades del cliente para que podamos predecir cuántas ventanas de cajero deben ser accesibles para las personas en sillas de ruedas. El modelo de colas M/M/1 describe el tiempo entre llegadas como una variable aleatoria exponencial con promedio de 1 cliente/λ (digamos 6 minutos) y el tiempo de servicio como una variable aleatoria exponencial con promedio de 1 cliente/μ (digamos 4 minutos).
Un modelo nunca es exactamente correcto; siempre debes recordar la frase “ es solo un modelo” . Por ejemplo, el modelo de colas M/M/1 supone que los clientes llegan a la tarifa promedio de 1 cliente cada 6 minutos, o 10 clientes por hora. En realidad, la tasa de llegada probablemente varía a lo largo del día.
Un IE crea un modelo para extraer información; el bucle del modelo a sí mismo se denomina “ análisis” . Los IE utilizan algunos modelos con bastante frecuencia y los IE pueden usar resultados matemáticos que otros han demostrado. Por ejemplo, para el modelo de colas M/M/1 se puede utilizar para calcular el número promedio de personas en la cola.
La línea etiquetada como “interpretación” es donde el IE interpreta los resultados matemáticos del modelo de regreso al sistema del mundo real. Ahora el IE debe volver a recordar “es solo un modelo” por lo que las predicciones pueden no ser perfectas. Dado que el modelo de colas M/M/1 asume una tasa de llegada promedio constante, los resultados usando λ = 10 clientes por hora solo se pueden aplicar al periodo del día con esa tasa de llegada. Podría ser necesario un modelo separado para la hora del almuerzo, que probablemente esté más ocupado.
Los IE son responsables de la eficiencia, incluido el uso eficiente del tiempo y los recursos. Ya sabes por clase de cálculo cómo encontrar el máximo o mínimo de una función y el cálculo es una herramienta que utilizan los IE. Sin embargo, los IE a menudo necesitan maximizar o minimizar una función lineal, lo que suena fácil, pero encontrar la solución no es fácil cuando hay muchas variables y también algunas restricciones. El siguiente es un ejemplo de tal problema.
El ganado lechero tiene diversos requerimientos de nutrientes, como proteínas, calcio y potasio, que pueden ser cubiertos por diferentes tipos de alimento, como alfalfa, maíz y mazorcas de maíz. El lechero quiere mezclar un pienso para las vacas lecheras que cumpla con los requerimientos de nutrimentos al costo mínimo. A continuación se muestra una versión muy simplificada del Problema de la Dieta aplicada a la alimentación de ganado lechero. La siguiente tabla da el contenido de nutrientes (proteína y potasio) de ciertos alimentos (alfalfa, maíz y mazorcas de maíz), así como el requerimiento nutritivo para proteínas y potasio (como porcentaje del alimento) y el costo de alfalfa, maíz y mazorcas de maíz (en $/tonelada).
Por ejemplo, la alfalfa es 28% de proteína, 0.26% de potasio, y cuesta $160 por tonelada. La alfalfa es una buena fuente de proteínas y una fuente media de potasio, pero es cara. El maíz es una fuente media de proteínas y una buena fuente de potasio, y es más barato que la alfalfa. Las mazorcas de maíz no son una buena fuente de proteínas ni de potasio, pero como por lo demás son un producto de desecho, son libres. Pensando un poco, se puede ver que la mezcla óptima probablemente necesitará alfalfa para cumplir con el requerimiento de proteína, maíz para cumplir con el requerimiento de potasio y mazorcas de maíz para mantener el costo bajo.
Queremos determinar cómo mezclar el alimento, es decir, qué fracción debe ser alfalfa (A), maíz (H) y mazorcas de maíz (C). Utilizaremos la programación lineal para resolver este problema, expresando la situación como minimizando una función objetivo lineal (costo) sujeta a restricciones lineales (proteína y potasio). Debido a que las unidades del ingrediente están representando porcentajes del conjunto, también sabemos que A+H+C=1.
Aquí está la formulación de programación lineal:

Este modelo es un ejemplo de un modelo de programación lineal. Podemos resolverlo matemáticamente. También hay programas informáticos que pueden ayudarnos a resolver este tipo de problemas. Excel es uno de esos programas aunque existen mejores herramientas para resolver modelos LP.
Este problema es un ejemplo de cómo los ingenieros industriales utilizan las matemáticas para promover la eficiencia. En este caso, ayudamos al agricultor a utilizar sus recursos de manera eficiente para mantener el ganado sano mientras minimizamos el costo del alimento. Este modelo es un ejemplo de un modelo LP, o, más ampliamente, un ejemplo de un modelo de optimización determinista . “ Determinístico ” significa que el modelo no tiene probabilidades y “ optimización ” significa que encontramos lo óptimo, o mejor, solución.
Un modelo LP es solo un tipo de modelo de optimización determinista. En realidad, en este ejemplo asumimos que podemos comprar cualquier cantidad real de ingredientes. Si fuera necesario comprar sólo en cantidades enteras un LP no sería un modelo apropiado. Un modelo donde las variables de decisión deben ser números enteros se denomina modelo de programación de enteros (IP).
Los ingenieros industriales deben ser capaces de reconocer situaciones en las que se pueda aplicar un modelo determinista, crear un modelo apropiado y resolver el modelo utilizando una herramienta adecuada. La siguiente lista describe situaciones en las que un modelo de optimización determinista podría ser útil.
- Mezcla de productos — determinar cuánto de cada tipo de producto hacer sujeto a restricciones en los recursos disponibles.
- Programación de producción: determinar qué cantidad de cada tipo de producto se debe hacer en diferentes períodos de tiempo para cumplir con las cantidades de producción especificadas en ciertos momentos.
- Mezcla — determinar la mejor mezcla de insumos a utilizar para minimizar el costo de producción de una mezcla. Nuestro ejemplo de alimentación fue un modelo de mezcla.
- Cortar stock — determinar la mejor manera de cortar material de recursos para maximizar las ganancias. Por ejemplo, un tronco se puede cortar en madera de varias dimensiones que se puede vender por diferentes cantidades.
- Staffing — determinar la mejor manera de asignar personas a trabajos para maximizar su preferencia o maximizar la productividad, en función de sus habilidades en diferentes trabajos.
- Transporte: determine la mejor manera de enrutar los recursos a través de una red de transporte para minimizar el costo, mientras entrega la cantidad adecuada de recursos a cada ubicación.
- Asignación — determinar la mejor manera de asignar recursos a las tareas.
- Problema de vendedor ambulante — determinar la mejor ruta entre una serie de puntos que visita cada punto al menos una vez.
Ejercicios


