5.6: Muestreo aleatorio de funciones de distribución

En el capítulo 2, los valores de atributo de entidad y el tiempo entre llegadas de entidades, así como los tiempos de operación y transporte se modelaron utilizando distribuciones de probabilidad. Además, los valores para estas variables deben asignarse a cada entidad. Para lograr esta asignación, se debe tomar una muestra aleatoria de la distribución de probabilidad correspondiente. Este tema es digno de una larga y minuciosa discusión como la prevista en Law (2007) así como Carson, Banks, Nelson y Nicol (2009). Aquí se presenta un enfoque para tomar muestras aleatorias para ilustrar cómo se aborda este tema.

Considere el tiempo entre llegadas de entidades en las dos estaciones de trabajo en un modelo en serie: exponencial (10) segundos, donde 10 es el tiempo promedio entre llegadas, TBA. Esta cantidad sigue la función de distribución acumulativa:

\(\ y=F(x)=1-e^{-x / T B A}=1-e^{-x / 10}\)

y por lo tanto

\ begin {align} x=-T B A\ ln (1-y) =-10\ ln (1-y)\ tag {5-1}\ end {align}

De la misma manera, el tiempo de servicio en la estación de trabajo A se distribuye uniformemente entre un valor mínimo y un valor máximo (5 y 13 segundos) y por lo tanto sigue la función de distribución acumulativa:

\(\ \mathrm{y}=\mathrm{F}(\mathrm{x})=(\mathrm{x} \text { -minimum) } /(\text { maximum }-\text { minimum })=(\mathrm{x}-5) /(13-5)\)

y por lo tanto

\(\ \begin{align}x=y^{*}(\text { maximum - minimum })+\text { minimum }=y^{*}(13-5)+5\tag{5-1}\end{align}\)

Observe que tomar la inversa de la distribución acumulativa reduce cada caso al mismo problema, determinando el valor de y, así, este enfoque para tomar una muestra aleatoria se denomina método de transformación inversa.

La Figura 5-2 muestra cómo funciona este método para el tiempo de servicio en la estación de trabajo A. Cualquier valor de y en el rango 0-1 es igualmente probable. (Esto se debe a que y es una distribución acumulativa.) Un buen procedimiento experimental requiere una muestra aleatoria y por lo tanto se debe elegir una muestra aleatoria de y. Una vez que se selecciona un valor aleatorio para y, la muestra aleatoria de x es sencilla de calcular.

Figura 5-2: Ilustración del método de transformación inversa

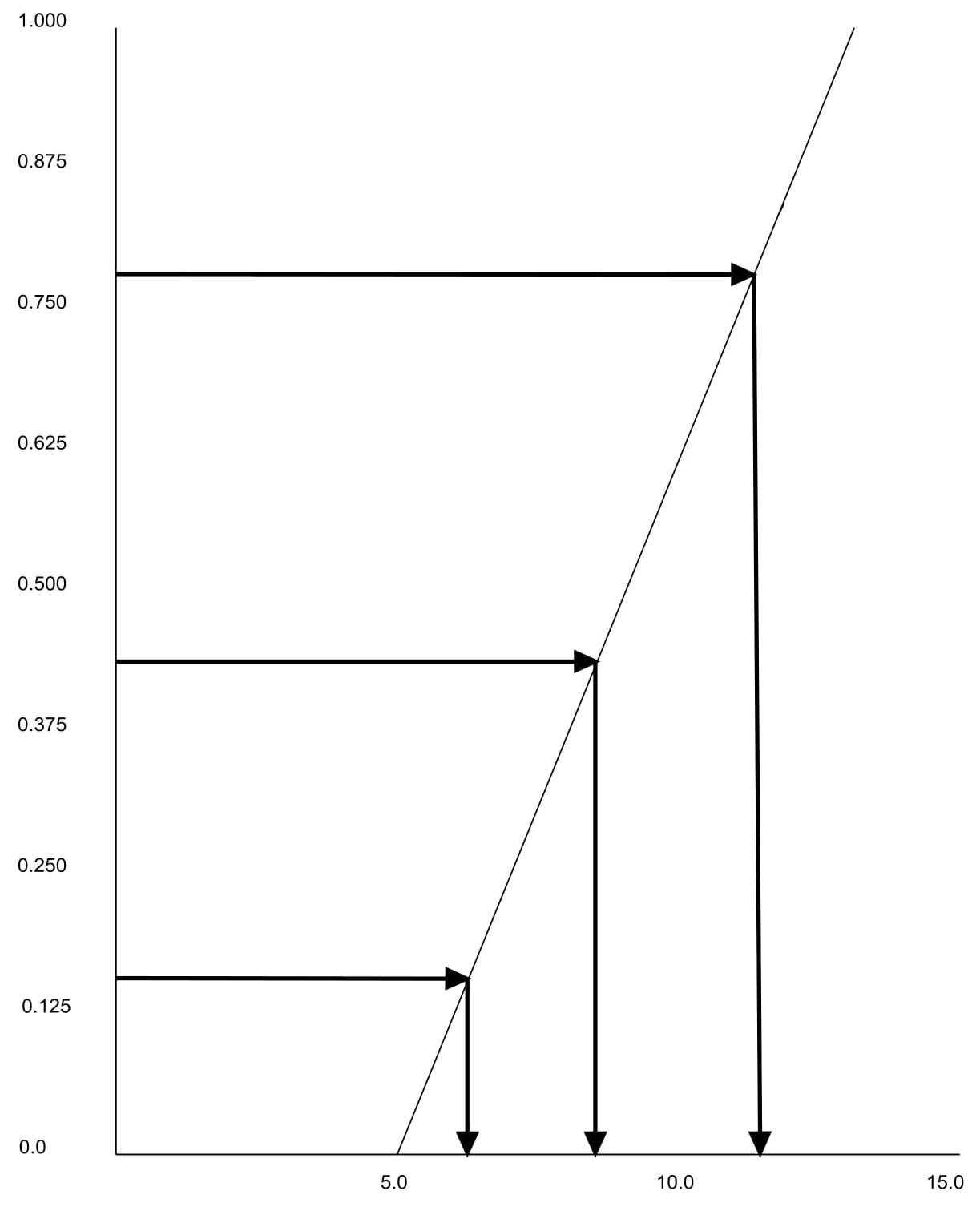
El método de transformación inversa se resume de la siguiente manera:

1. Determinar la inversa de la función de distribución acumulativa, F ^-1 (x).
2. Cada vez que se necesita una muestra:
   1. Generar una muestra aleatoria, r, distribuida uniformemente en el rango de 0 a 1.
   2. x = F ^-1 (r).

El uso del método de transformación inversa requiere que exista la inversa de la función de distribución acumulativa. Esto es cierto para las siguientes distribuciones comúnmente utilizadas en modelos de simulación: uniforme, triangular, exponencial, weibull y cualquier distribución discreta donde se enumera la función de masa, así como una distribución heurística en forma de histograma.

Como ejemplo, considere el uso del método de transformación inversa con la ecuación 5-2. Supongamos que r se selecciona para ser 0.45. Entonces x = -10 ln (1 — 0.43) = 5.62. A continuación se aplica el método de transformación inversa a la ecuación 5-5. Supongamos que r se selecciona para ser 0.88. Entonces x = 0.88 * (13 - 5) + 5 = 12.04.