Saltar al contenido principal
LibreTexts Español

2.7: Resolver ODEs con Mathematica- Cómo encontrar soluciones numéricas y analíticas a ODEs con Mathematica

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    85612

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Autores: Matthew Baumgartner, Olyvia Dean, Viral Patel, Joel Schweitzer y Eric Van Beek

    Administradores: Brian Hickner, Lennard Gan, Addison Heather, Monique Hutcherson

    Fecha de lanzamiento: 6 de septiembre de 2006 /Fecha de revisión: 8 de septiembre de 2007

    Introducción

    Mathematica es un programa de soluciones matemáticas avanzadas creado por Wolfram Research, Inc. Uno de los paquetes de software más potentes de su tipo, Mathematica es capaz de resolver fácil y convenientemente fórmulas matemáticas complicadas, incluyendo ecuaciones diferenciales. Este artículo se centra en el modelado de Ecuaciones Diferenciales Ordinarias (ODE) de primer orden y superior en las siguientes formas:

    \[\frac{d y}{d x}=f(x, y) \tag{Basic ODE} \]

    \[\frac{d y^{z}}{d^{z} x}=f(x, y) \tag{Higher Order ODE} \]

    Como todo el software, Mathematica utiliza un lenguaje específico para realizar cálculos. Los nombres de todas las funciones deben estar en mayúscula- esto se aplica tanto a las funciones matemáticas (como Sin y Cos) como a las funciones incorporadas (como Plot y DSolve). Por esta razón es común que los usuarios escriban sus propias funciones en letras minimizadas. Esto disminuye la posibilidad de anular o redefinir una función de Mathematica. Los corchetes siempre siguen las llamadas de función y los parámetros de la función siempre están encerrados entre corchetes curvos. Por ejemplo, si un usuario desea trazar sin (x) de x = 0 a x = 1, escribiría: Parcela [Sin [x], {x,0,1}]. El usuario debe escribir “Shift"+"Enter” para ingresar la función. Al escribir solo “Enter” se agregará una línea a la fórmula. Para teclados completos de PC, la tecla “Enter” en el extremo derecho es el equivalente a “Shift” +” Enter”. Si el usuario no quiere ver la línea de salida, se puede suprimir escribiendo un punto y coma al final de la expresión. Mathematica también reconoce constantes matemáticas comunes como pi (Pi), constante de Euler (E) y números imaginarios (I). Tenga en cuenta que estas constantes también se deben poner en mayúscula cuando se ingresan.

    Mathematica cuenta con dos funciones para resolver ODEs: dSolve y ndSolve. DSolve se usa cuando el usuario desea encontrar la función o funciones generales que resuelven la ecuación diferencial, y NDSolve se usa cuando el usuario tiene una condición inicial. Las indicaciones para las funciones son bastante similares. Nota: Se deben usar dos signos iguales para denotar igualdad en una ecuación. El uso de un signo igual asigna un valor a una variable.

    Ejemplo:

    f (x) = 5 x 2 + 7 Esta entrada crea una variable llamada f (x) que tiene un valor de 5 x 2 + 7.

    f (x) = = 5 x 2 + 7 Esta entrada crea una función f (x) la cual se define por 5 x 2 + 7.

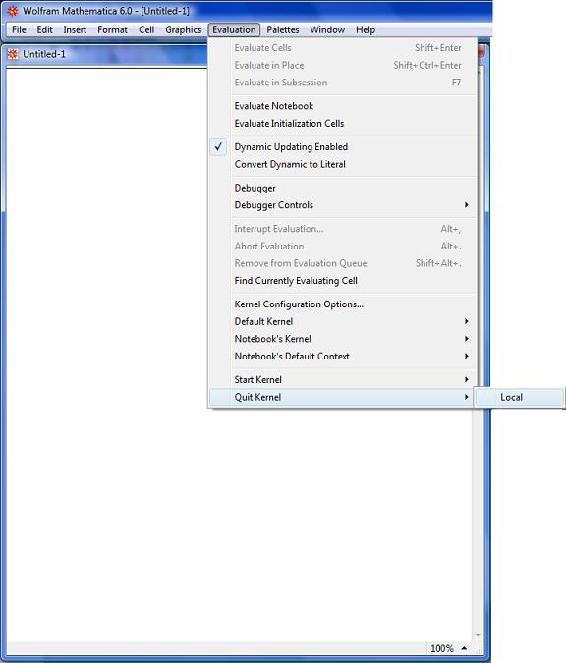
    Mathematica a veces almacenará funciones o variables creadas por el usuario en su caché. Esto hace que algunos comandos (potencialmente) correctos generen errores. Se recomienda salir del kernel local y reinicializar los comandos después de cualquier cambio en su código.

    lear kernel example.jpg

    Además, verifique que se esté ejecutando cada comando en el código. Borrar todas las salidas en la celda puede ser útil para averiguar qué comandos no se habían ejecutado. Esto se puede hacer yendo a la opción “Celda” que se encuentra en la parte superior y eligiendo el Ejemplo “Eliminar toda la salida”:

    La salida no se borra

    example.jpg de salida nclear

    CORRECCIÓN DE SALIDAS

    ejemplo de salida nclear en cell.jpg

    CÓDIGO CON SALIDAS ABaprendió la salida example.jpg

    Como se ve en los ejemplos, es más fácil solucionar problemas y depurar su programa cuando parece menos confuso. Borrar las salidas adicionales te ayuda a enfocarte solo en el código que has escrito.

    ODEs de primer orden

    Notación: En los siguientes ejemplos, eqn representa la ODE, y representa la función para la que se está resolviendo, i representa la condición inicial, y x y t son variables independientes.

    ODE con condiciones iniciales

    ndSolve no mostrará un valor numérico, sino una “Función de interpolación” que se puede mostrar gráficamente. La forma más fácil de mostrar esta gráfica es asignar la solución a una variable (llamada Solución en el ejemplo) en la línea de entrada, y luego usar la función “Trazar” para mostrarla.

    Entrada para una ODE: Solución = ndSolve [{eqn, y [0] == i}, y, {x, xmin, xmax}]

    Entrada para múltiples ODEs: Solución = ndSolve [{eqn1, eqn2,... , y1 [0] == i1, y2 [0] == i2,... }, {y1, y2,... }, {x, xmin, xmax}]

    Entrada para Ecuaciones Diferenciales Parciales: Solución = ndSolve [{eqn, y [0] == i}, y, {x, xmin, xmax}, {t, tmin, tmax}]

    Después de que Mathematica resuelva la ODE, grafica la solución escribiendo: Trazar [Evaluar [y [x] /. Solución], {x, xmin, xmax}], donde “/.” es una notación utilizada por Mathematica que significa “siguiendo la regla de”. Básicamente recuerda la función almacenada como la variable en la línea de entrada anterior. Dependiendo de las necesidades del usuario, también pueden ser útiles las funciones “ParametricPlot” o “Plot3D”. La notación para estas funciones es la misma que “Trama”.

    Aquí hay un ejemplo simple de lo que escribirías en Mathematica:

    • Solución = ndSolve [{y' [x] ==y [x] *Cos [x+y [x]], y [0] ==1}, y, {x,0,30}]

    Mathematica generará:

    • Salida [1] =
      ParseError: invalid Primary (click for details)
      Callstack:
    at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/02:_Fundamentos_de_Modelado/2.07:_Resolver_ODEs_con_Mathematica-_Cómo_encontrar_soluciones_numéricas_y_analíticas_a_ODEs_con_Mathematica), /content/body/div[2]/div[1]/ul[2]/li/span, line 1, column 3

    Para trazar esta función escribirías:

    • Trazar [Evaluar [y [x] /.Solución], {x,0,30}]

    Nota: Recuerde escribir “Shift"+"Enter” para ingresar la función

    ODEs sin condiciones iniciales

    Entrada para una ODE: DSolve [eqn, y, x]

    Entrada para múltiples ODEs: DSolve [{eqn1, eqn2,...}, {y1, y2,...}, x]

    Entrada para una Ecuación Diferencial Parcial: DSolve [eqn, y, {x1, x2,...}]

    Aquí hay un ejemplo simple de lo que escribirías en Mathematica:

    • Solución = DSolve [y' [x] ==4*x-2*x*y [x], y [x], x]

    Mathematica generará:

    • Salida [1] =
      ParseError: invalid Primary (click for details)
      Callstack:
    at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/02:_Fundamentos_de_Modelado/2.07:_Resolver_ODEs_con_Mathematica-_Cómo_encontrar_soluciones_numéricas_y_analíticas_a_ODEs_con_Mathematica), /content/body/div[2]/div[2]/ul[2]/li/span, line 1, column 8

    ODEs de Segundo Orden y Superiores

    Entrada para ODEs de orden superior: Solución = ndSolve [{eqn, y [0] == i1, y' [0] == i2,...}, y, {x, xmin, xmax}]

    Trazando la solución: Trazar [Evaluar [{y [x], y' [x],...} /. Solución], {x, xmin, xmax}]

    Aquí hay un ejemplo simple de lo que escribirías en Mathematica:

    • Solución = ndSolve [{y [x] +Sin [y [x]] +y [x] ==0, y [0] ==1, y' [0] ==0, y, {x,0,30}]

    Mathematica generará:

    • Salida [1] =
      ParseError: invalid Primary (click for details)
      Callstack:
    at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/02:_Fundamentos_de_Modelado/2.07:_Resolver_ODEs_con_Mathematica-_Cómo_encontrar_soluciones_numéricas_y_analíticas_a_ODEs_con_Mathematica), /content/body/div[3]/ul[2]/li/span, line 1, column 3

    Para trazar esta función escribe:

    • Trazar [Evaluar [{y [x], y' [x], y [x]} /.Solución], {x,0,30}]

    Mathematica debe generar una gráfica.

    Algoritmos utilizados por Mathematica

    Mathematica utiliza dos algoritmos principales para determinar la solución a una ecuación diferencial. Estos algoritmos son el método Adams y el método Gear.

    Los métodos Adams y Gear son formas de métodos lineales de múltiples pasos. Un ejemplo de estos sería el siguiente:

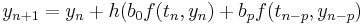
    y_ {n+1} = y_ {n} + h (b_0 f (t_n, y_n) + b_p f (t_ {n-p}, y_ {n-p})\

    En el ejemplo anterior, h denota el tamaño del paso y los coeficientesb_0,\ lpuntos, b_s son determinados por el método utilizado. Los métodos multipaso son expansiones de métodos de un solo paso más familiares utilizados para resolver diferenciales (es decir, Euler, Runge-Kutta, Taylor). Cada uno de estos métodos requiere de un punto inicial para poder calcular el siguiente punto. De manera similar, los métodos multipaso también requieren puntos iniciales para resolver la ODE. El número de puntos iniciales requeridos depende del método que se utilice para resolver la ODE. Los métodos de varios pasos suelen producir menos errores que los métodos de un solo paso debido a múltiples puntos iniciales.

    Para determinar qué método usar primero hay que encontrar la rigidez de la función.

    Método Adams

    Los métodos de Euler, Taylor y Runge-Kutta utilizaron puntos cercanos al valor de la solución para evaluar funciones derivadas. El método Adams-Bashforth analiza la derivada en valores de solución antiguos y utiliza ideas de interpolación junto con la solución actual y derivada para estimar la nueva solución [4]. Para resolver una ODE usando este método, f (t, y) debe ser continuo y cumplir con la condición de Lipschitz para la variable y que establece [5]:

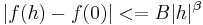
    |f (h) - f (0) | <= B |h|^ {\ beta}\

    para todos | h | < ε donde B y β son independientes de h, β > 0 y α es un límite superior para todos los β para los que existe un B finito

    Esta es una forma básica del método Adams-Bashforth. Tenga en cuenta que se requieren dos puntos iniciales para este método.

    y_ {n+1} = y_n + h [\ beta_1 f (y_n, t_n) +\ beta_2 f (y_ {n-1}, t_ {n-1})]\

    Hay otro método Adams que requiere tres puntos iniciales. El método se resuelve de la misma manera, sin embargo la ecuación varía un poco y se le conoce como el Método Adams-Moulton.

    y_ {n+1} = y_n + h [\ beta_0 f (y_ {n+1}, t_ {n+1}) +\ beta_1 f (y_n, t_n) +\ beta_2 f (y_ {n-1}, t_ {n-1})]\

    Los coeficientes/restricciones, β se pueden resolver para usar el conocimiento de OD's y otras herramientas matemáticas. Se dijo anteriormente que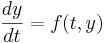\ frac {dy} {dt} = f (t, y). Podemos dejar que f (t, y) = λ y, por lo tanto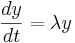\ frac {dy} {dt} =\ lambda y. También podemos dejar que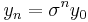y_n =\ sigma^ {n} y_0\ si hay un tamaño de paso constante y σ representa un polinomio. A través de la sustitución encontramos [6]:

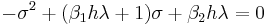
    -\ sigma^ {2} + (\ beta_1 h\ lambda + 1)\ sigma +\ beta_2 h\ lambda = 0\

    Podemos expandir la cuadrática usando otra identidad matemática y finalmente resolver las restricciones β 1 y β 2. Otro método para resolver los coeficientes β 1, β 2 se menciona a continuación:

    Para encontrar el coeficiente β j se debe usar primero la interpolación polinómica para encontrar el polinomio p de grado s − 1 de tal manera que:

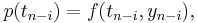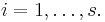
    p (t_ {n-i}) = f (t_ {n-i}, y_ {n-i}),\ qquadparai=1,\ lpuntos, s.

    A partir de esto, la fórmula de Lagrange para interpolación polinómica produce

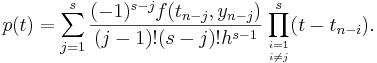
    p (t) =\ suma_ {j=1} ^s\ frac {(-1) ^ {s-j} f (t_ {n-j}, y_ {n-j})} {(j-1)! (s-j)! h^ {s-1}}\ prod_ {i=1\ sobre i\ ne j} ^s (t-t_ {n-i}).

    Ahora el polinomio p es una aproximación localmente buena del lado derecho de la ecuación diferencial y '= f (t, y) que se va a resolver. Ahora debemos considerar la ecuación y '= p (t) en su lugar. Esta ecuación se puede resolver exactamente simplemente tomando la integral de p.

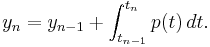
    y_n = y_ {n-1} +\ int_ {t_ {n-1}} ^ {t_n} p (t)\, dt.

    El método Adams-Bashforth surge cuando se sustituye la fórmula para p. Los coeficientes b j resultan ser

    \[\\beta_j = \frac{(-1)^{s-j}}{(j-1)!(s-j)!} \int_0^1 \prod_{i=1 \atop i\ne j}^s (u+i) \,du. \nonumber \]

    El método Adams-Bashforth se usa típicamente para ODE's lineales y no Liner con sistemas densos.

    Método de Engranaje

    Tomando

    \[\\beta_i = 0\ \nonumber \]

    para i ≥ 1

    El método Gear, también conocido como las fórmulas de diferenciación hacia atrás (BDF, también conocidas como fórmulas de Gear) es otro método de varios pasos pero generalmente se usa para múltiples ecuaciones. Para usar el método de engranaje su función debe tener una rigidez mayor a 500, lo que significa que la función es rígida.

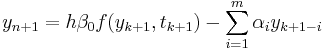
    _ {n+1} = h\ beta_0f (y_ {k+1}, t_ {k+1}) -\ suma_ {i=1} ^m\ alpha_i y_ {k+1-i}\

    Como casos particulares, tomar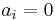a_i = 0\ para i ≥ 2 y optimizar los coeficientes restantes para maximizar la precisión del esquema resultante recupera el método implícito de Euler. Tomando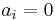_i = 0\ para i ≥ 3 da

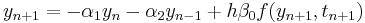
    _ {n+1} = -\ alfa_1 y_n -\ alfa_2 y_ {n-1} + h\ beta_0 f (y_ {n+1}, t_ {n+1})\

    Ahora nos centramos en este caso en particular. Aplicando este método al problema del modelo escalar y asumiendo la constante h y una solución de la forma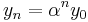y_n =\ alfa^n y_0\, encontramos la siguiente ecuación cuadrática para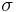\ sigma\

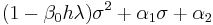
    (1-\ beta_0 h\ lambda)\ sigma^2 +\ alpha_1\ sigma +\ alpha_2\

    las dos raíces de las cuales están dadas por

    \[\\sigma=\frac {-\alpha_1 + \sqrt{\gamma(1+\epsilon)}}{2(1-\Sigma)} or \frac {-\alpha_1 - \sqrt{\gamma(1+\epsilon)}}{2(1-\Sigma)}\ \nonumber \]

    \[\\gamma = \alpha_1^2-4\alpha_2\ \nonumber \]

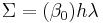
    Sigma = (\ beta_0) h\ lambda\

    Aplicando las identidades, podemos expandir ambas raíces en términos de poderes de h. Por nuestra forma asumida de la solución, se deduce que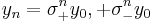_n=\ sigma_+^n y_0, +\ sigma_-^n y_0 .El término de orden principal en la expansión en h de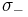sigma_-\ (una “raíz espuria”) es proporcional a h. Para h pequeñas, decae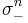sigma_-^n rápidamente a cero, y así puede descuidarse. Los términos de orden inicial en la expansión en h de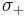sigma_+\ (la “raíz física”) se asemejan a la expansión de la serie Taylor de la solución exacta en un solo lapso de tiempo.

    sigma_+ = (-\ frac {\ alpha_1} {2} +\ frac {\ sqrt {\ gamma}} {2}) +\ beta_0 (-\ frac {\ alpha_1} {2} +\ frac {\ sqrt {\ gamma}} {2} [1+\ frac {2\ alpha_2} {\ gamma}])\ lambda h +\ beta_0^2 (-\ frac {\ alpha_1} {2} +\ frac {\ sqrt {\ gamma}} {2} [1+\ frac {2\ alpha_2} {\ gamma} -\ frac {2\ alpha_2} {\ gamma^2}])\ lambda^2 h^2 +...

    Coincidiendo coeficientes con la expansión de la solución exacta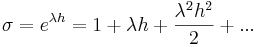sigma = e^ {\ lambda h} = 1 +\ lambda h +\ frac {\ lambda^2h^2} {2} +... como lo indican los underbrackets en la expresión anterior, y aplicando la definición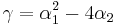gamma =\ alpha_1^2 - 4\ alpha_2\, llegamos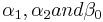alpha_1,\ alpha_2 y\ beta_0\ a tres ecuaciones para lograr el mayor orden de precisión posible con esta forma. Se verifica fácilmente que satisfacen estas tres ecuaciones. El término de error de orden inicial de este método es proporcional a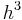^3\. Por lo tanto, en un solo período de tiempo, el esquema es “localmente preciso de tercer orden”; más significativamente, durante un intervalo de tiempo fijo [0, T], el esquema es globalmente preciso de segundo orden. El método resultante,

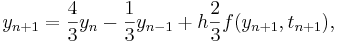
    _ {n+1} =\ frac {4} {3} y_n -\ frac {1} {3} y_ {n-1} + h\ frac {2} {3} f (y_ {n+1}, t_ {n+1}),

    se conoce así como BDF2, y puede verse como una alternativa implícita a AM3 que, para el mismo número de pasos en el pasado, p = max (m, n), tiene un orden de precisión reducido pero un dominio de estabilidad mucho mejorado. Los BDF de orden superior pueden derivarse de manera análoga; se encuentra que BDF3, BDF4, BDF5 y BDF6 en particular tienen excelentes propiedades de estabilidad en comparación con sus homólogos de AM con el mismo número de etapas.

    Funcionó Ejemplo 1

    Se le ha asignado un reactor no isotérmico con los siguientes balances de material y entalpía.

    \[\\frac {dc_a}{dt} = c_a(t)^2-c_b(t)- T(t)^2 \nonumber \]Especies a Balance de materiales

    \[\\frac {dc_b}{dt} = c_b(t)^3 - c_a(t)- T(t)^2 \nonumber \]Especies b Balance de materiales

    \[\\frac {dT}{dt} = c_a(t) - c_b(t) - T(t)^2 \nonumber \]Balance de entalpía

    ¿Cuándo es igual la concentración de las especies a y b? Las condiciones iniciales para el reactor son las siguientes:

    T 0 = 1

    c a 0 = 2.0

    c b 0 = 1.8

    t f = 0.2

    s = ndSolve [{x' [t] == x [t] ^2 - y [t] - z [t] ^2, y' [t] == y [t] ^3 - x [t] - z [t] ^2, z' [t] == x [t] - y [t] - z [t] ^2, x [0] == 2, y [0] == 1.8, z [0] == 1}, {x, y, z}, {t, 0.2}]

    Parcela [Evaluar [{x [t], y [t]} /. s], {t, 0, 0.2}]

    rror en el Método de Euler

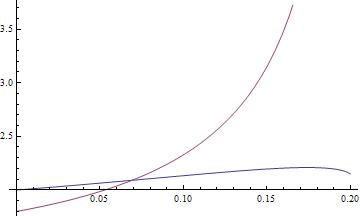
    Funcionó Ejemplo 2

    Se le ha pedido que estudie un reactor semidiscontinuo para la reacción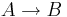\ fila derecha B. La ley de tarifas es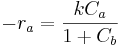r_a=\ frac {kC_a} {1+C_b}, donde k = 2.7. Otros parámetros son: volumen inicial = 5, caudal volumétrico = 0.05, concentración inicial de A = 2500. Utilice Mathematica para crear una gráfica de conversión versus tiempo para 100 unidades de tiempo.

    1. Balance de Topes:

    \[\\frac{dX}{dt} = - \frac{r_aV}{N_{A0}} \nonumber \]

    2. Ley de tarifas:

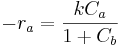
    r_a=\ frac {kC_a} {1+C_b}

    3. Estequiometría:

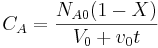
    C_A =\ frac {N_ {A0} (1-X)} {v_0+v_0t}

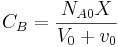
    C_B=\ frac {N_ {A0} X} {v_0+v_0}

    4. Combinar:

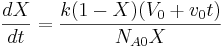
    frac {dX} {dt} =\ frac {k (1-X) (v_0+v_0t)} {N_ {A0} X}

    Si el reactor semidiscontinuo funciona por 100 unidades de tiempo, la conversión es de aproximadamente 0.8. Esto se puede ver en la trama de abajo o ejecutando los dos comandos que siguen en Mathematica.

    s = ndSolve [{y' [t] == 2.7 (1 - y [t]) (5 + .05 t)/(2500 y [t]), y [0] == 0.0001}, y, {t, 0, 100}];

    Parcela [Evaluar [y [t] /. s], {t, 0, 100}, PloRange -> Todos]

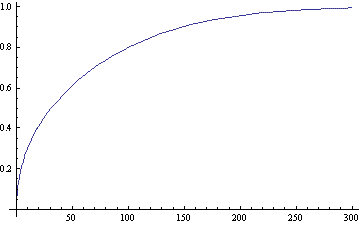
    athmaticaEx2.gif

    Este es el archivo del cuaderno de Mathematica para el ejemplo: Media:MathematicaEX2.nb

    Nota: Los parámetros utilizados en este problema son fabricados y están destinados a ilustrar el uso de Mathematica en la resolución de ODEs.

    Formateo de gráficas en Mathematica

    Aquí hay algunos consejos útiles para formatear gráficas en Mathematica:

    Parcela de Etiquetas: por ejemplo, Parcela [Sin [x], {x,0,2Pi}, PlotLabel->"Volumen de Tanque vs Tiempo”]

    Ejes de Etiquetas: por ejemplo, Trazar [Sin [x], {x,0,2Pi}, Ejeslabel-> {"tiempo (min)”, "volumen (L) "}]

    Parcela de color: e.g. Trama [Sin [x], {x,0,2Pi}, Plotstyle->Rojo]. También puede hacer que la trama sea gruesa, discontinua, etc. por ejemplo, Plot [Sin [x], {x,0,2Pi}, Plotstyle-> {Rojo, Grueso, Discontinuo}]

    Insertar leyenda: por ejemplo Necesita ["plotLegends`"] <—DEBE insertar esto ANTES de su comando de trazado. Trama [{Sin [x], Cos [x]}, {x,0,2Pi}, PlotLegend-> {"seno”, “coseno"}]

    Rincón del sabio

    Resolución de ODEs con Mathematica Video

    video.google.com/googleplayer. swfd=5007050669435611182

    diapositivas para esta charla

    Consejos y trucos adicionales para la solución de problemas en Mathematica

    Mathematica es una poderosa herramienta informática, sin embargo la sintaxis puede ser un poco difícil de entender. Aquí hay algunas notas para la solución de problemas en Mathematica.

    1. Verifique que sus nombres y signos de variables sean consistentes.

    • Ej) Asegúrate de usar xI en todas partes en lugar de xI y x1 o xl.
    • Ex) Las funciones, incluidas las que creas, suelen ir seguidas de corchetes como Sin [x] o y [x]. Sin embargo, los corchetes no son necesarios cuando se está resolviendo para una función en un conjunto de ecuaciones diferenciales como ndSolve [eqns, {y}, {x, 0, 50}];
    • Ej) Comprueba si tus paréntesis están alineados de tal manera que realmente estás ingresando la función que crees que estás ingresando. Recordar orden de operaciones y la propiedad distributiva. x* (a+b) NO es igual (x*a) + b Esto parece simple, pero a menudo se pasa por alto cuando se trata de varias líneas de código.

    2. Puede que le resulte más fácil definir todas sus variables juntas al comienzo de su código. Esto facilita retroceder y cambiar los valores asignados a cada variable si se intenta determinar el impacto que una variable tiene en un sistema de ecuaciones. Por ejemplo, digamos que está tratando de determinar los efectos que tendrán los caudales en dos tanques diferentes (F1, F2) sobre los volúmenes del tanque en diez pasos de tiempo. 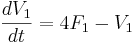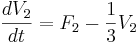Las ecuaciones diferenciales que rigen la situación son:\ frac {dV_1} {dt} = 4F_1 - V_1 y\ frac {dV_2} {dt} = F_2 -\ frac {1} {3} V_2, donde F1 = 2, F2 = 12, V1 (0) = 0, V2 (0) = 0.

    Si escribes las ODEs en Mathematica sustituyendo directamente en F1 = 2 y F2 = 12, tendrás que cambiar las ODEs cada vez que cambies los valores de F1 y F2. A continuación se muestra un ejemplo de cómo serían las ecuaciones de Mathematica.

    s = ndSolve [{V1' [t] == 8 — V1 [t], V2' [t] == 12 — (1/3) *V2 [t], V1 [0] == 0, V2 [0] == 0}, {V1, V2}, {t,0,10}]

    Otra opción es definir F1 y F2 antes de tus ecuaciones, y luego llamarlas al resolver para tus ODEs. Esto le permite sustituir fácilmente en nuevos valores sus variables sin cambiar las ecuaciones diferenciales, y reduce las probabilidades de cometer errores computacionales simples en su ODE en el proceso. El código de Mathematica se vería como se muestra a continuación.

    variables = {F1 -> 2, F2 -> 12};

    s = ndSolve [{V1' [t] == 4*F1 — V1 [t], V2' [t] == F2 — (1/3) *V2 [t], V1 [0] == 0, V2 [0] == 0} /. variables, {V1, V2}, {t,0,10}]

    3. Tenga en cuenta el Kernel

    El Núcleo de Mathematica almacena toda la información sobre las definiciones de variables. Cuando define una variable, la definición se almacena allí. El kernel se inicia automáticamente cuando se inicia una nueva sesión de Mathematica. También puedes iniciarlo manualmente. Para iniciar el kernel manualmente vaya a Evaluación -> Iniciar Kernal -> Local. Una vez que se inicia el kernel y deseas volver atrás y cambiar una definición de variable debes “Salir del Kernal” antes de que veas que se produce el cambio. Para “Salir del Kernal” debes ir a Evaluación -> Salir de Kernal -> Local. Al terminar el Kernal de Mathematica, se borran todas las definiciones previamente ingresadas. Por esta razón, después de “Salir del Kernal” e ingresar nuevas definiciones para sus variables debe volver a ingresar todo su código. Las siguientes imágenes muestran cómo “Iniciar Kernal” y cómo “Salir del Kernal”.

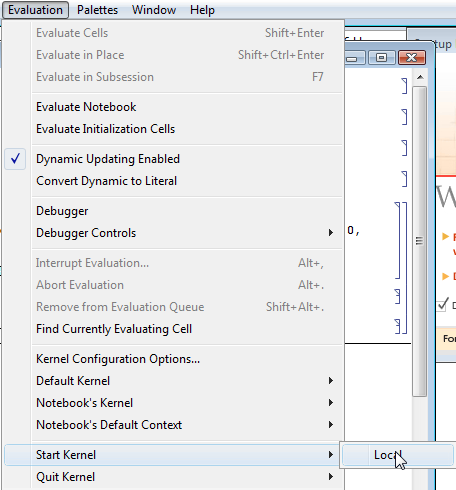
    tartkernel.png

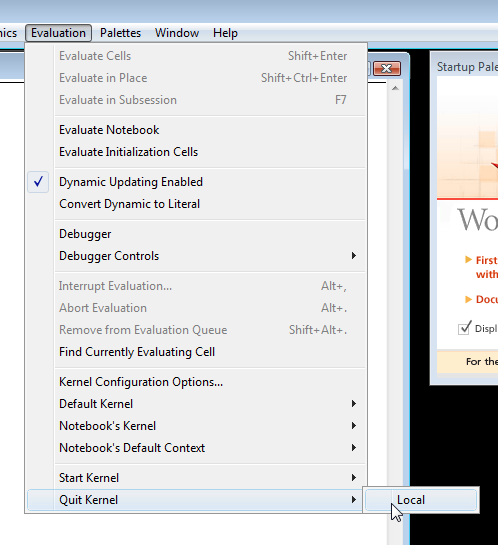
    uitkernal.png

    Ejemplo:

    Un ejemplo de cuándo querría “Salir del Kernal” al usar Mathematica para Controles es cuando encuentra un punto de estado estacionario usando un controlador PID. Comenzamos definiendo las variables para vset, taui, taud y Kc. Mathematica resuelve esta ecuación usando las variables definidas y muestra que (x->3.9, V->10) es el punto de estado estacionario. Esto se muestra en la figura 1 a continuación.

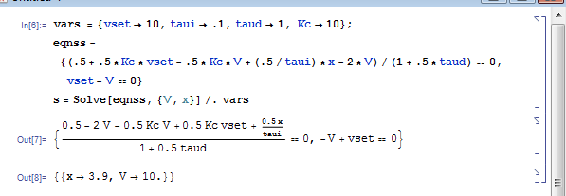
    ernel1.png
    Figura 1 cuando definió Kc aunque no lo haya definido aquí.
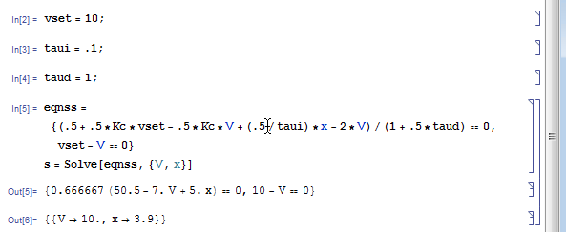
    ernel2.png
    La Figura 3 muestra la salida una vez que tiene “Quit the Kernel” y volvió a ingresar el código de Mathematica.

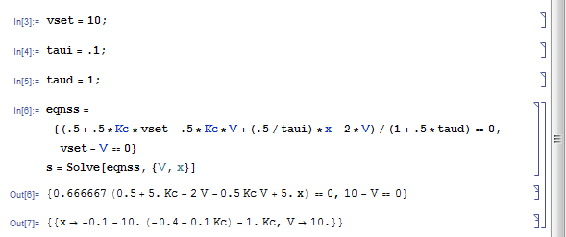
    ernel3.png

    Ahora se ve que la definición de Kc ha sido eliminada porque los puntos de estado estacionario son en términos de Kc. Para encontrar el impacto de Kc puedes usar esta solución.

    4. Definir funciones o fórmulas que se utilizan a menudo

    Si va a utilizar una función a menudo y no está ya definida en Mathematica por defecto, defina la suya propia. Esto puede ser especialmente útil si tiene la intención de repetir la misma función varias veces mientras solo cambia las variables. Un escenario en el que definir su propia función podría ahorrarle tiempo y error es al comparar los valores de P-Fisher manteniendo constantes los márgenes. Sólo cambiarán las variables pero la función seguirá siendo la misma. La nueva función sólo durará tanto tiempo como cada sesión en Mathematica.

    Para definir una función, comience nombrando la función seguida de un corchete abierto. Enumere todas las variables con un guión bajo después de cada nombre y separe cada variable con una coma. Cierre el corchete cuando todas las variables hayan sido listadas. Para que Mathematica sepa que esta es una función recién definida, después de cerrar el paréntesis coloque un punto y coma y signo igual. Ahora defina cuál es la fórmula usando los nombres de las variables. Cuando haya terminado, haga clic en Mayús-Intro simultáneamente. Para probar la nueva fórmula, comience con el nombre de la función y abra el corchete, luego enumere todas las variables valores numéricos separados por comas en el mismo orden que se listó al definir la función. Cierre el corchete después de que todas las variables hayan sido listadas y haga clic en Mayús-Entrar simultáneamente El resultado será la siguiente línea en Mathematica con la respuesta.

    Ejemplo:

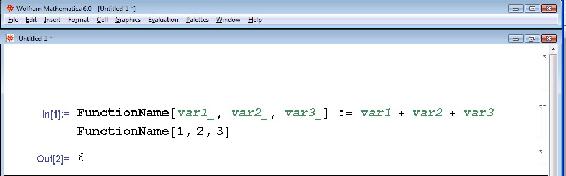
    efiningFunctions.jpg

    También es posible utilizar esta herramienta para poner ecuaciones en términos de variables desconocidas. Para ello comienza definiendo la función de la misma manera que antes. Al conectar los valores numéricos de las variables, deje las variables desconocidas como su nombre de variable. El resultado de Mathematica proporcionará la respuesta en términos de las variables desconocidas.

    Ejemplo:

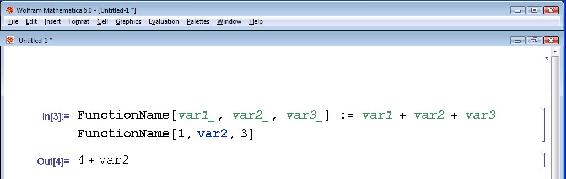
    efiningFunctions2.jpg

    5. “Que sea bonita”

    A menudo, cuando las personas programan en cualquier idioma, tienden a aglomerar líneas, casi como si estuvieran tratando de ahorrar papel. Bueno, ya que esto no aplica cuando estás escribiendo en una pantalla, no te preocupes por ello.

    • Ex) Podrías escribir:

    vars = {V -> 1000, Cao -> 0.2, UA -> 20000, F -> 2000, DE1 -> 30000, k1 -> 1.0 10^13, DH1 -> 50000, rcp -> 60, R -> 1.987, Para -> 500, Tf -> 500, Tjin -> 500, Fj -> 1000, Vj -> 100, Caf -> 0.2, DH2 -> -192000, DE2 -> 30000, k2 -> 1.0 ^13};

    eqns = {Ca' [t] == (Caf - Ca [t])) /V - Ca [t] *K1*exp [-DE1/ (R*T [t])], Cb' [t] == (0 - Cb [t]) /V +K1*Ca [t] *Exp [-DE1/ (R*T [t])] - K2*CB [t] *Exp [-DE2/ (R*T [t])], T' [t] == (Tf - T [t]) /V + (-DH1/ (rcp)) *K1*Ca [t] *Exp [-DE1/ (R*T [t])] + (-DH2/RCP) *K2*CB [t] *Exp [-DE2/ (R*T [t])] - (UA (T [t] - Tj [t]))/(V *rcp), Tj [t] == (Fj (Tjin - Tj [ t]))/Vj + (UA (T [t] - Tj [t]))/(Vj *rcp), Ca [0] == 0.2, Cb [0] == 0, T [0] == 500, Tj [0] == 500};

    sol = ndSolve [eqns /.vars, {Ca, Cb, T, Tj}, {t, 0, 50}]; Parcela [{Ca [t]} /. sol, {t, 0, 50}, axesLabel -> {t, Ca}, PloRange -> Completo]; Parcela [{Cb [t]} /. sol, {t, 0, 50}, AxesLabel -> {t, Cb}, PloRange -> Completo]; Parcela [{T [t]} /. sol, {t, 0, 50}, AxesLabel -> {t, T}, PloRange -> Completo]; Parcela [{Tj [t]} /. sol, {t, 0, 50}, AxesLabel -> {t, Tj}, PloRange -> Completo]

    • pero se ve mucho mejor si haces esto:

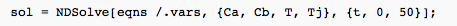
    Imagen

    Imagen

    Imagen

    Imagen

    Es de esperar que estos pensamientos te ayuden más adelante y faciliten la lectura de tu código.

    6.) “¡Comprueba los colores!”

    Aquí hay una lista de color de fuente que Mathmatica emitirá por una razón específica.

    Variables locales en un determinado color de fuente

    Variables locales de Módulo y Con en Verde

    1. Ejemplo:odule.jpg

    Argumentos de función y nombres de patrones en verde (cursiva)

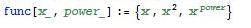
    1. Ejemplo:unction.jpg

    Variables hechas especiales por uso en argumentos en Turquesa

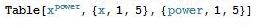
    • Ejemplo:ariables.jpg

    Errores y advertencias en un determinado color de fuente

    Errores de Sintaxis en Púrpura

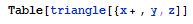
    • Ejemplo:yntax.jpg

    Errores de Sintaxis Enfatizados en Rojo Oscuro con Fondo Amarillo

    • Ejemplo:mphasized.jpg

    Faltan argumentos en Rojo Brillante

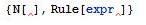
    1. Ejemplo:issing.jpg

    Exceso de argumentos en Rojo Brillante

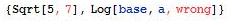
    1. Ejemplo:xcess.jpg

    Posibles asignaciones no deseadas en Rojo Brillante

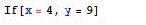
    • Ejemplo:nwanted.jpg

    Nombres de opciones no reconocidos en Rojo Brillante

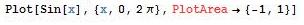
    • Ejemplo:nrecognized.jpg

    Conflictos de alcance local en rojo oscuro con fondo amarillo

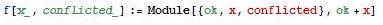
    • Ejemplo:ocal.jpg

    Variables que quedarán fuera de alcance antes de ser utilizadas en Rojo Brillante

    • Ejemplo:ariables out.jpg

    Sombreado en múltiples contextos en Rojo Brillante

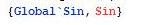
    • Ejemplo:hadowing.jpg

    Otro en cierto Color de Fuente

    Comentarios en Gris Claro

    • Ejemplo:omment.jpg

    Cuerdas en Gris Oscuro

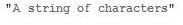
    • Ejemplo:trings.jpg

    Símbolos globales que no tienen valor asignado en Azul Brillante

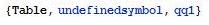
    • Ejemplo:lobal.jpg

    Acceder a Mathematica desde su computadora personal

    Si prefiere usar Mathematica desde la computadora de su hogar en lugar de una en el campus, puede iniciar sesión remotamente en una computadora CAEN a través del servicio de Sitios Virtuales de U-M. Siga los pasos que se detallan a continuación:

    1. Visita http://virtualsites.umich.edu/. Aparecerá la página de U-M WEBLOGIN. Inicie sesión con su nombre único y contraseña de Kerberos.
    2. La página de Sitios Virtuales debería aparecer en tu pantalla. Haga clic en el botón grande, naranja Conectar ahora.
    3. Bajo el epígrafe ¿Qué software necesitas? , seleccione Ingeniería (CAEN) Legacy XP. Luego haga clic en el botón Solicitar conexión hacia la parte inferior de la página.
    4. Siga las instrucciones bajo el encabezado Iniciar sitios virtuales descargando y abriendo el archivo en la barra de información de Internet Explorer. Aparecerá una ventana en su pantalla titulada Conexión a Escritorio remoto. Haga clic en el botón Conectar.
    5. Después verá la pantalla que aparece al iniciar sesión en una computadora CAEN. Tu nombre único ya debería estar incluido. Escriba su contraseña Kerberos y haga clic en Aceptar para iniciar sesión en la computadora CAEN.
    6. Haga clic en Aceptar en la ventana Aviso que aparece y se aplicará su configuración personal. También haga clic en Aceptar si aparece una ventana del Asistente para requisitos del sistema.
    7. Si te desplazas hacia abajo usando la barra de desplazamiento en el lado derecho de la pantalla, verás el botón Inicio. Haga clic en Inicio -> Todos los programas -> Métodos matemáticos y numéricos -> Wolfram Mathematica -> Mathematica 6. Una vez que Mathematica se abre en la pantalla de la computadora, puedes usarlo como si realmente estuvieras sentado frente a una computadora CAEN en el campus.
    8. Para cerrar sesión, haga clic en Inicio -> Cerrar sesión. En la ventana Cerrar sesión de Windows, haga clic en Cerrar sesión.

    Referencias

    • “Método Adams”, Wolfram MathWorld, Online: 5 de agosto de 2007. Disponible http://mathworld.wolfram.com/AdamsMethod.html [1]
    • “Método Gear Predictor-Corrector”, Universidad Davidson, Online 5 de agosto de 2007. Disponible http://webphysics.davidson.edu/Projects/SuFischer/node47.html [2]
    • Fogler, H. Scott (2006), Elementos de Ingeniería de Reacciones Químicas, Nueva Jersey: Pretince Hall PTR. ISBN 0-13-047394-4 [3]
    • “Adams-Bashforth”, Pitt Math, En línea: 8 de septiembre de 2007. Disponible: www.math.pitt.edu/~sussmanm/2071spring07/lab02/index.html #AdamsBashforthMethods [4]
    • “Lipschitz Condition”, Wolfram MathWorld, Online: 7 de septiembre de 2007. Disponible http://mathworld.wolfram.com/LipschitzCondition.html [5]
    • “Adams-Bashforth (AB) Methods”, Universidad de California-San Diego, En línea: 7 de septiembre de 2007. Disponible: renaissance.ucsd.edu/capters/chap11.pdf [6]
    • “Método Gears”, Universidad de California-San Diego, En línea: 7 de septiembre de 2007. Disponible: renaissance.ucsd.edu/capters/chap11.pdf [7]
    • Utilice el estilo Harvard References para las referencias en el documento.
    • Para más información sobre cuándo hacer referencia consulta la siguiente entrada de Wikipedia.

    This page titled 2.7: Resolver ODEs con Mathematica- Cómo encontrar soluciones numéricas y analíticas a ODEs con Mathematica is shared under a CC BY 3.0 license and was authored, remixed, and/or curated by Peter Woolf et al. via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.