2.6: Resolución numérica de ODE en Excel- Método de Euler, Runge Kutta, Tiempo muerto en resolución de ODE

Autores: (Presentada: 9/8/06 /Fecha de revisión: 9/19/06) Aaron Bennick, Bradley Anderson, Michael Salciccioli

Mayordomos: (5/9/07) Sean Gant, Jay Lee, Lance Dehne, Kelly Martin

Introducción

Este artículo se centra en el modelado de ecuaciones diferenciales ordinarias (ODEs) de la forma:

\[\frac{d y}{d x}=f(x, y) \nonumber \]

Al crear un modelo,\(y_{i + 1}\) se genera un nuevo valor utilizando el valor antiguo o inicial y _i, la estimación de pendiente φ y el tamaño de paso h. Esta fórmula general se puede aplicar de manera escalonada para modelar la solución. Todos los modelos paso a paso tomarán la siguiente forma general:

\[y_{i+1}=y_{i}+\phi h \nonumber \]

Los métodos de modelado discutidos en este artículo son el método de Euler y los métodos Runge-Kutta. La diferencia entre los dos métodos es la manera en que se estima la pendiente φ.

Elegir el modelo y el tamaño de paso adecuados

El método de modelado numérico adecuado depende en gran medida de la situación, los recursos disponibles y la precisión deseada del resultado. Si solo se requiere una estimación rápida de una ecuación diferencial, el método de Euler puede proporcionar la solución más simple. Si se requiere una precisión mucho mayor, se puede usar un método Runge-Kutta de quinto orden. Los ingenieros de hoy, con la ayuda de computadoras y excel, deberían ser capaces de estimar de manera rápida y precisa la solución a las ODE utilizando métodos Runge-Kutta de orden superior.

En todos los modelos numéricos, a medida que disminuye el tamaño del paso, se incrementa la precisión del modelo. La compensación aquí es que los tamaños de paso más pequeños requieren más cómputos y, por lo tanto, aumentan la cantidad de tiempo para obtener una solución. Se puede lograr un equilibrio entre la precisión deseada y el tiempo requerido para producir una respuesta seleccionando un tamaño de paso apropiado. Un algoritmo sugerido para seleccionar un tamaño de paso adecuado es producir modelos usando dos métodos diferentes (posiblemente un Runge-Kutta de segundo y tercer orden). El tamaño de los pasos se puede cortar sistemáticamente a la mitad hasta que la diferencia entre ambos modelos sea aceptablemente pequeña (creando efectivamente una tolerancia de error).

Método de Euler

El método de Euler es un método simple de un solo paso que se usa para resolver ODEs. En el método de Euler, la pendiente, φ, se estima de la manera más básica utilizando la primera derivada en x _i. Esto da una estimación directa, y el método de Euler toma la forma de

\[y_{i+1}=y_{i}+f\left(x_{i}, y_{i}\right) h \nonumber \]

Para la demostración, utilizaremos la ecuación diferencial básica\(\frac{d y}{d x}=3 x^{2}+2 x+1\) con la condición inicial y (0) = 1. Si un tamaño de paso, h, se toma para ser 0.5 en el intervalo de 0 a 2, las soluciones se pueden calcular de la siguiente manera:

x	Y_Euler	Y_real	Error
y (0)	1	1	0
y (0.5)	1 + [3 (0) ^2 + 2 (0) + 1] (0.5) = 1.5	1.875	0.375
y (1)	1.5 + [3 (0.5) ^2 + 2 (0.5) + 1] (0.5) = 2.875	4	1.125
y (1.5)	2.875 + [3 (1) ^2 + 2 (1) + 1] (0.5) = 5.875	8.125	3.25
y (2.0)	5.875 + [3 (1.5) ^2 + 2 (1.5) + 1] (0.5) = 11.25	15	3.75

Los valores y_reales en esta tabla se calcularon integrando directamente la ecuación diferencial, dando la solución exacta como: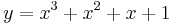

Uso de Microsoft Excel

Calcular una solución de ODE a mano con el método de Euler puede ser un proceso muy tedioso. Afortunadamente, este proceso se simplifica enormemente mediante el uso de Microsoft Excel. Crear una hoja de cálculo similar a la anterior, donde se especifican los valores x y los valores Y_EULER se calculan recursivamente a partir del valor anterior, hace que el cálculo sea bastante simple. Se puede utilizar cualquier tamaño de paso e intervalo.

Inconveniente del método de Euler

Hay varios inconvenientes en el uso del método de Euler para resolver ODEs que deben tenerse en cuenta. En primer lugar, este método no funciona bien en las ODE rígidas. Una ODE rígida es una ecuación diferencial cuyas soluciones son numéricamente inestables cuando se resuelven con ciertos métodos numéricos. Para ecuaciones rígidas, que se encuentran frecuentemente en el modelado de la cinética química, los métodos explícitos como los de Euler suelen ser bastante ineficientes porque la región de estabilidad es tan pequeña que el tamaño del paso debe ser extremadamente pequeño para obtener cualquier precisión. En un caso como este, un método implícito, como el método de Euler al revés, produce una solución más precisa. Estos métodos implícitos requieren más trabajo por paso, pero la región de estabilidad es mayor. Esto permite un tamaño de paso más grande, haciendo que el proceso general sea más eficiente que un método explícito. Un segundo inconveniente de usar el Método de Euler es que se introduce error en la solución. El error asociado con el ejemplo simple anterior se muestra en la última columna. Este error se puede ver visualmente en la gráfica de abajo.

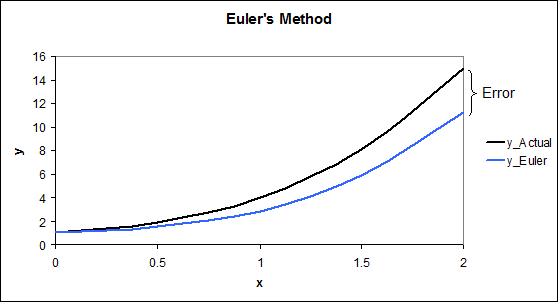
Se puede observar que los dos valores son idénticos en la condición inicial de y (0) =1, y entonces el error aumenta a medida que aumenta el valor x y el error se propaga a través de la solución a x = 2. El error se puede disminuir eligiendo un tamaño de paso más pequeño, lo que se puede hacer con bastante facilidad en Excel, o optando por resolver la ODE con el método Runge-Kutta más preciso.

Métodos Runge-Kutta

El método Runge-Kutta para modelar ecuaciones diferenciales se basa en el método de Euler para lograr una mayor precisión. Se realizan estimaciones derivadas múltiples y, dependiendo de la forma específica del modelo, se combinan en un promedio ponderado a lo largo del intervalo de paso. El orden del método Runge-Kutta puede variar de segundo a mayor, dependiendo de la cantidad de estimaciones derivadas realizadas. El método Runge-Kutta de segundo orden etiquetado como técnica de Heun estima derivadas promediando las mediciones de punto final del tamaño del paso a lo largo de una función. Este valor promedio se utiliza como estimación de pendiente para x _{i + 1}. Los métodos Runge-Kutta de tercera y mayor potencia hacen estimaciones de derivadas de punto medio y entregan un promedio ponderado para la derivada de punto final en x _{i + 1}. A medida que aumenta el orden Runge-Kutta, también lo hace la precisión del modelo.

La forma general del método Runge-Kutta es

\[y_{i+1}=y_{i}+\phi\left(x_{i}, y_{i}, h\right) h \nonumber \]

Donde\(φ(x_i,y_i,h)\) ahora representa una pendiente promedio ponderada a lo largo del intervalo\(h\).

\[\phi\left(x_{i}, y_{i}, h\right)=a_{1} k_{1}+a_{2} k_{2}+\ldots+a_{n} K_{n} \nonumber \]

donde las a son constantes y las k son

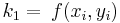
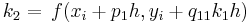
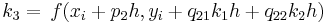
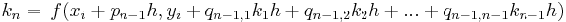
Las constantes a, p y q se resuelven con el uso de expansiones de la serie Taylor una vez que se especifica n (ver al final de la página para la derivación). El conjunto resultante de ecuaciones tiene uno o más grados de libertad. Esto significa que por cada orden del método Runge-Kutta, hay una familia de métodos. A continuación se presentan algunas de las opciones más comunes de Runge-Kutta.

Métodos Runge-Kutta de segundo orden (n = 2)

Cada método de segundo orden descrito aquí producirá exactamente el mismo resultado si la ecuación diferencial modelada es constante, lineal o cuadrática. Debido a que este no suele ser el caso, y la ecuación diferencial suele ser más complicada, un método puede ser más adecuado que otro.

Técnica de Heun

El método Runge-Kutta de segundo orden con una iteración de la estimación de pendiente, también conocida como técnica de Heun, establece las constantes

\[a_1=a_2=\ce{1/2} \nonumber \]

y

\[p_1=q_{11}=1. \nonumber \]

Huen determinó que definiendo\(a_1\) y\(a_2\) como\(1/2\) tomará el promedio de las pendientes de las líneas tangentes en cada extremo del intervalo deseado, teniendo en cuenta la concavidad de la función, creando un resultado más preciso. Cuando se sustituye en la forma general, encontramos

\[y_{i+1}=y_{i}+\left(\frac{1}{2} k_{1}+\frac{1}{2} k_{2}\right) h \nonumber \]

con k ₁ y k ₂ definidos como

\[k_{1}=f\left(x_{i}, y_{i}\right) \nonumber \]

\[k_{2}=f\left(x_{i}+h, y_{i}+h k_{1}\right) \nonumber \]

Para la demostración de este método Runge-Kutta de segundo orden, utilizaremos la misma ecuación diferencial básica\(\frac{d y}{d x}=3 x^{2}+2 x+1\) con la condición inicial y (0) = 1. Si un tamaño de paso, h, se toma para ser 0.5 en el intervalo de 0 a 2, las soluciones se pueden calcular de la siguiente manera:

Figura 1: Runge-Kutta de segundo orden

x	k_1	k_2	Y_Heun	Y_real	Error
y (0)	3 (0) ^2 + 2 (0) + 1 = 1	3 (0.5) ^2 + 2 (0.5) + 1 = 2.75	1	1	0
y (0.5)	3 (0.5) ^2 + 2 (0.5) + 1 = 2.75	3 (1) ^2 + 2 (1) + 1 = 6	1 + [0.5 (1) + 0.5 (2.75)] (0.5) = 1.9375	1.875	-0.0625
y (1)	3 (1) ^2 + 2 (1) + 1 = 6	3 (1.5) ^2 + 2 (1.5) + 1 = 10.75	2.375 + [0.5 (2.75) + 0.5 (6)] (0.5) = 4.125	4	-0.125
y (1.5)	3 (1.5) ^2 + 2 (1.5) + 1 = 10.75	3 (2) ^2 + 2 (2) + 1 = 17	5.375 + [0.5 (6) + 0.5 (10.75)] (0.5) = 8.3125	8.125	-0.1875
y (2.0)	3 (2) ^2 + 2 (2) + 1 = 17	3 (2.5) ^2 + 2 (2.5) + 1 = 24.75	10.75 + [0.5 (10.75) + 0.5 (17)] (0.5) = 15.25	15	-0.25

Cuando se compara con la demostración del método de Euler anterior, se puede observar que la Técnica de Runge-Kutta Heun de segundo orden requiere un aumento significativo en el esfuerzo para producir valores, pero también produce una reducción significativa en el error. Siguiendo los métodos de Runge-Kutta se pueden trabajar de manera similar, agregando columnas para valores k adicionales. A continuación se muestra una descripción gráfica de cómo se estima la pendiente utilizando tanto el método de Euler como la técnica de Heun. Observe el aumento de precisión cuando se usa una pendiente promedio a través de un intervalo de 0.5 en lugar de solo una estimación inicial.

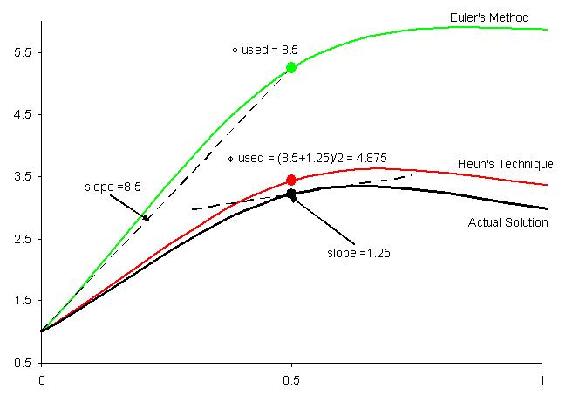
Método de polígono mejorado

Usando el método de polígono mejorado, un ₂ se toma como 1, un ₁ como 0, y por lo tanto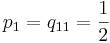. La forma general entonces se convierte en

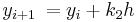
con k ₁ y k ₂ definidos como

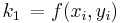
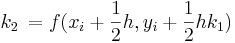
Método de Ralston

El método de Ralston toma un ₂ para ser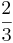. Por lo tanto 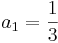y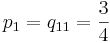. Se ha determinado por Ralston (1962) y Ralston y Rabinowitz (1978) que definir un ₂ como 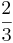minimizará el error de truncamiento en los métodos Runge-Kutta de segundo orden. La forma general se convierte en

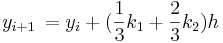
con k ₁ y k ₂ definidos como

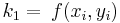
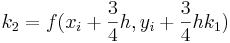
Métodos Runge-Kutta de tercer orden (n = 3)

Los métodos Runge-Kutta de tercer orden, cuando se derivan, producen una familia de ecuaciones para resolver constantes con dos grados de libertad. Esto significa que se puede producir una familia aún más variable de métodos Runge-Kutta de tercer orden. Un formulario general de tercer orden comúnmente utilizado es

con

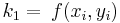
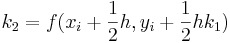
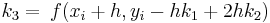
Métodos Runge-Kutta de Cuarto Orden (n = 4)

La familia de métodos Runge-Kutta de cuarto orden tiene tres grados de libertad y, por lo tanto, una variabilidad infinita al igual que lo hacen los métodos de segundo y tercer orden. Las versiones de cuarto orden son las más favorecidas entre todos los métodos de Runge-Kutta. Lo que se conoce como el método clásico Runge-Kutta de cuarto orden es

con

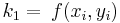
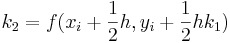
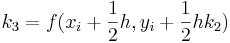
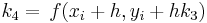
Métodos Runge-Kutta de quinto orden (n = 5)

Cuando se requieran resultados muy precisos, se debe emplear el método RK de quinto orden Runge-Kutta Butcher's (1964) de quinto orden:

con

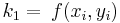
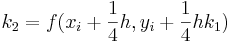
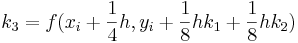
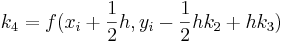
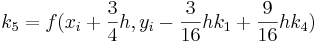
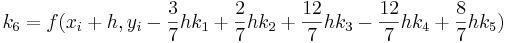
La integración de k 's dentro de otros valores k sugiere el uso de una hoja de cálculo. Al igual que con todos los métodos de Runge-Kutta, el cálculo de valores para la versión de quinto orden sería de gran ayuda mediante el uso de Microsoft Excel.

Comparación de modelos interactivos en Excel

Para dar una mejor comprensión del impacto entre los diferentes métodos de Runge-Kutta, así como el impacto del tamaño del paso, la hoja de excel interactiva a continuación le permitirá ingresar el tamaño de paso h en un conjunto de modelos y observar cómo los modelos contornean para que coincida con una solución de ecuación diferencial de ejemplo.

Observe la relación entre el tipo de modelo, el tamaño del paso y el error relativo.

Hoja de cálculo interactiva de comparación de modelos ODE

Tiempo Muerto

El tiempo muerto, o ecuación diferencial de retardo, ocurre cuando hay un retraso o retraso en el proceso de una función de la vida real que se está modelando. Esto significa que el modelo numérico no es exacto hasta que termina el retraso. Este concepto puede entrar en juego para el inicio de un proceso de reacción. Por ejemplo, al inicio de una reacción en un CSTR (Reactor de Tanque Agitado Continuo), habrá reactivos en la parte superior del reactor que hayan iniciado la reacción, pero tardará un tiempo determinado para que estos reactantes/productos se descarguen del reactor. Si se estuviera modelando la concentración de reactivos frente al tiempo, el tiempo t=0 habría comenzado cuando se llenó el tanque, pero las concentraciones que se leen no seguirían una ecuación modelo estándar hasta que se completara el tiempo de residencia y el reactor estuviera en modo operativo continuo. El tiempo muerto es el tiempo que tardaría en que las lecturas comiencen a cumplir con una ecuación teórica, o el tiempo que tarda en limpiarse el reactor una vez de los reactivos originales. El tiempo muerto se puede determinar experimentalmente y luego insertarse en ecuaciones de modelado.

La solución de tal ecuación diferencial de retardo se vuelve problemática porque para resolver la ecuación, se necesita información de tiempos pasados (durante el retraso) además del tiempo actual. Por ejemplo, si t _o es el tiempo de retraso para el escenario dado, entonces el valor a usar en la ODE se convierte en (t- t _o) en lugar de t Al modelar esto en excel, (x- t _o) se sustituye por el valor x. Con esta sustitución, el método de Euler se puede utilizar nuevamente de la misma manera para aproximar la solución. Esta sustitución se llevará a la ecuación diferencial para que la nueva solución de tiempo muerto pueda aproximarse utilizando el método de Euler. Para modelar el reactor antes de que se complete el tiempo muerto inicial, a menudo se utilizan funciones por partes. De esta manera para el tiempo muerto, se usa un modelo dado no característico del reactor en condiciones normales de operación, luego una vez que se completa el tiempo muerto se toma en efecto la ecuación de modelado.

El siguiente enlace ayudará a mostrar cómo incluir el tiempo muerto en una aproximación de método numérico como el método de Euler. Como se ve en el archivo excel, el tiempo muerto que es especificado por el usuario en el cuadro amarillo cambiará el retraso en el modelo. Cuanto más tiempo muerto, más desplazado de la ecuación teórica es el nuevo modelo. Para tomar en cuenta el tiempo muerto en excel, el valor x simplemente se sustituye por (x-t) donde t es igual al tiempo muerto. Si observas las ecuaciones ingresadas en las celdas Y, verás que el valor x insertado en la ecuación diferencial es (x-t), donde t es el tiempo muerto especificado por el usuario. Se puede ver a través de esta hoja de cálculo de ejemplo que el efecto del tiempo muerto es un simple desplazamiento horizontal en la ecuación del modelo.

Hoja de cálculo interactiva Dead Time

Error

Hay dos tipos de error asociados con la resolución de ODEs usando métodos de aproximación paso a paso en Excel. Estos errores también están presentes utilizando otros métodos o programas informáticos para resolver ODEs. El primero, la discretización, es el resultado del valor y estimado que es inherente al uso de un método numérico para aproximar una solución. Los errores de discretización, también llamados truncamiento, ocurren proporcionalmente en un solo tamaño de paso. El error de truncamiento se propagará sobre los resultados extendidos porque la aproximación de los pasos anteriores se utiliza para aproximar el siguiente. En esencia, se está haciendo una copia de una copia. La precisión del siguiente punto es un resultado directo de la precisión del anterior. Así como la calidad de una segunda copia depende de la calidad de la primera. Este error se puede reducir reduciendo el tamaño del paso.

Consulte la hoja de cálculo interactiva de comparación de modelos ODE para aprender mejor cómo los tamaños de paso pueden influir en el error.

Los segundos tipos de errores son los errores de redondeo. Estos errores dependen de la capacidad de la computadora para retener dígitos significativos. Cuantos más dígitos significativos pueda contener una computadora, menor será el error de redondeo.

Error de estimación en el método de Euler

Para representar matemáticamente el error asociado al método de Euler, primero es útil hacer una comparación con una expansión infinita de la serie Taylor del término y _{i + 1}. La expansión de la serie Taylor de este término es

\[y_{i+1}=y_{i}+f\left(x_{i}, y_{i}\right) \hbar+f^{\prime}\left(x_{i}, y_{i}\right) \frac{h^{2}}{2}+f^{\prime \prime}\left(x_{i}, y_{i}\right) \frac{h^{3}}{3}+\ldots+f^{n}\left(x_{i}, y_{i}\right) \frac{h^{n}}{! n} \nonumber \]

Cuando esta expansión se compara con la forma general del método de Euler se puede ver que el método de Euler carece de cada término más allá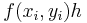. Estos términos faltantes, la diferencia entre la aproximación de Euler y una serie infinita de Taylor (tomada como la verdadera solución), es el error en la aproximación de Euler. La representación matemática del error en los métodos Runge-kutta de orden superior se realiza de manera similar.

Estimación y minimización de errores en el método Runge Kutta

Los pasos de tiempo uniformes son buenos para algunos casos pero no siempre. A veces nos ocupamos de problemas donde variar los pasos de tiempo tiene sentido. ¿Cuándo debes cambiar el tamaño del paso? Si tenemos un esquema de orden n y un esquema de orden n y (n+1) th, podemos tomar la diferencia entre estos dos como el error en el esquema, y hacer que el tamaño del paso sea más pequeño si preferimos un error más pequeño, o mayor si podemos tolerar un error mayor. Esto es bastante simple con Runge Kutta, porque podemos tomar un método de quinto orden y un método de cuarto orden usando las mismas k's. Solo un poco de trabajo extra en cada paso.

Otra forma de estimar el error en el método Runge-Kutta es invertir direcciones en cada paso de la solución de avance y recalcular la ordenada anterior. Al considerar la diferencia entre la ordenada anterior recién calculada y el valor calculado originalmente, puede determinar una estimación del error de truncamiento incurrido al avanzar la solución sobre ese paso. Esto es un poco más tedioso, pero sí da una buena estimación del error de truncamiento.

Método de Euler para Sistemas de ODEs

En ingeniería química y otros campos relacionados, tener un método para resolver una ecuación diferencial simplemente no es suficiente. Muchos problemas del mundo real requieren resolver simultáneamente sistemas de ODEs. Para problemas como estos, cualquiera de los métodos numéricos descritos en este artículo seguirá funcionando. La única diferencia es que para n ODEs, se necesitan n valores iniciales de y para el valor x inicial. Entonces el método numérico de elección solo se aplica a cada ecuación en cada paso antes de pasar al siguiente. Esto complica aún más la metodología de resolución de problemas paso a paso, y requeriría el uso de Excel en casi todas las aplicaciones. La ODE resuelta con el método de Euler como ejemplo antes ahora se expande para incluir un sistema de dos ODEs a continuación:

\[\frac{d y_{1}}{d x}=3 x^{2}+2 x+1, y_{1}(0)=1 \nonumber \]

\[\frac{d y_{2}}{d x}=4 y_{1}+x, y_{2}(0)=2 \nonumber \]

El tamaño del paso vuelve a ser 0.5, sobre un intervalo 0-2.

x	Y_1Euler	Y_2EULER	Y_1real	Y_2real	y_1 Error	y_2 Error
y (0)	1	2	1	2	0	0
y (0.5)	1 + [3 (0.5) ^2 + 2 (0.5) + 1] (0.5) = 2.375	2 + [4 (1) + 0.5] (0.5) = 4.25	1.875	5.875	-0.5	1.625
y (1)	2.375 + [3 (1) ^2 + 2 (1) + 1] (0.5) = 5.375	4.25 + [4 (2.375) + 1] (0.5) = 9.5	4	18.5	-1.375	9
y (1.5)	5.375 + [3 (1.5) ^2 + 2 (1.5) + 1] (0.5) = 10.75	9.5 + [4 (5.375) + 1.5] (0.5) = 21	8.125	51.875	-2.625	30.875
y (2.0)	10.75 + [3 (2) ^2 + 2 (2) + 1] (0.5) = 19.25	21 + [4 (10.75) + 2] (0.5) = 43.5	15	124	-4.25	80.5

Se debe observar que hay más error en la aproximación de Euler de la segunda solución de ODE. Esto se debe a que la ecuación también tiene y ₁ en ella. Entonces está el error introducido al usar la aproximación de Euler para resolver la 2da ODE, así como el error de la aproximación de Euler utilizada para encontrar y ₁ en la 1ª ODE en el mismo paso!

De nuevo se obtuvieron soluciones exactas de la integración directa de las ODE: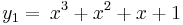 y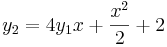

Ejemplo 1: Diseño del reactor

La reacción elemental en fase líquida A —> B se llevará a cabo en una PFR isotérmica isobárica a 30 grados C. La alimentación ingresa a una concentración de 0.25 mol/L y a una velocidad de 3 mol/min. Se sabe experimentalmente que la constante de reacción es 0.01 min ^-1 a esta temperatura. Se le ha dado la tarea de construir un reactor que se utilizará para llevar a cabo esta reacción. Usando el método de Euler con un tamaño de paso de 0.05, determine qué tan grande debe ser el reactor si se desea una conversión de 80%.

Ecuación de diseño simplificado:

\[\frac{d V}{d X}=\frac{F_{A 0}}{k C_{A 0}(1-X)} \nonumber \]

Agruñar el flujo, la concentración y la constante de reacción dados juntos da:

\[\frac{d V}{d X}=1200 \frac{1}{1-X} \nonumber \]

Dado que no se requiere volumen para una conversión de cero, la condición inicial necesaria es V (0) =0.

Ahora la información simplemente tiene que ser ingresada en Excel. Se utiliza una columna para la conversión, X, que va de 0 a 0.8 en incrementos de 0.05 para el tamaño del paso, y se sabe que el primer valor, V (0), es cero. Para obtener el volumen, simplemente agregue el volumen anterior a las constantes multiplicadas por el tamaño del paso y 1/ (1-X), o:

\[V_{i+1}=V_{i}+1200 * 0.05 * \frac{1}{1-X} \nonumber \]

Al copiar esta fórmula abajo de la columna hasta el valor de conversión final de 0.8, se dan los resultados que se muestran en la siguiente tabla:

X	V
V (0)	0
V (0.05)	63
V (0.1)	130
V (0.15)	200
V (0.2)	275
V (0.25)	355
V (0.3)	441
V (0.35)	533
V (0.4)	633
V (0.45)	743
V (0.5)	863
V (0.55)	996
V (0.6)	1146
V (0.65)	1317
V (0.7)	1517
V (0.75)	1757
V (0.8)	2057

El volumen final del reactor obtenido es de aproximadamente 2057 L. Esto se compara razonablemente bien con el valor exacto de 1931 L. El archivo Excel utilizado para obtener esta solución, junto con la solución exacta, se puede descargar a continuación.

Ejemplo 1

Derivación Runge-Kutta de segundo orden

El siguiente ejemplo te llevará paso a paso a través de la derivación de los métodos Runge-Kutta de segundo orden. Establecer n = 2 da como resultado una forma general de

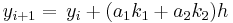
con k ₁ y k ₂ definidos como

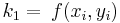
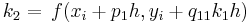
Deben definirse las constantes en la forma general. Para ello emplearemos una expansión de la serie Taylor de segundo orden para y _{i + 1} en términos de y _i y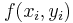. Esta serie de Taylor es

\[y_{i+1}=y_{i}+f\left(x_{i}, y_{i}\right) h+f^{\prime}\left(x_{i}, y_{i}\right) \frac{h^{2}}{2} \nonumber \]

Expandirse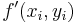 con la regla de la cadena, y sustituirla de nuevo en la expansión anterior de la serie Taylor da

\[y_{i+1}=y_{i}+f\left(x_{i}, y_{i}\right) h+\left(\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y} \frac{\partial y}{\partial x}\right) \frac{h^{2}}{2} \nonumber \]

El siguiente paso es aplicar una expansión de la serie Taylor a la ecuación k ₂. La regla de expansión de la serie Taylor aplicada es

\[g(x+r, y+s)=g(x, y)+r \frac{\partial g}{\partial x}+s \frac{\partial g}{\partial y}+\ldots \nonumber \]

y la ecuación resultante es

\[f\left(x_{i}+p_{1} h, y_{i}+q_{11} k_{1} h\right)=f\left(x_{i}, y_{i}\right)+p_{1} h \frac{\partial f}{\partial x}+q_{11} k_{1} h \frac{\partial f}{\partial y}+O\left(h^{2}\right) \nonumber \]

donde O (h ²) es una medida del error de truncamiento entre el modelo y la solución verdadera.

Cuando este resultado de expansión de la serie Taylor de la ecuación k ₂, junto con la ecuación k ₁, se sustituye en la general, y se realiza una agrupación de términos similares, se obtienen los siguientes resultados:

\[y_{i+1}=y_{i} \quad\left[a_{1} f\left(x_{i}, y_{i}\right) | a_{2} f\left(x_{i}, y_{i}\right)\right] h\left|\left[a_{3} p_{1}^{\partial f}\left|a_{s} q_{11} f\left(x_{i}, y_{i}\right)_{\partial y}^{\partial f}\right| h^{2} | O\left(h^{3}\right)\right.\right. \nonumber \]

Establecer este resultado igual a la forma general sustituida nos permitirá determinar que, para que estas dos ecuaciones sean equivalentes, las siguientes relaciones entre constantes deben ser verdaderas.

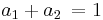
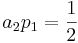
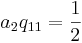
Cabe destacar que estas tres ecuaciones, que relacionan constantes necesarias, tienen cuatro incógnitas. Esto significa que para resolver tres constantes, primero se debe elegir una. Esto da como resultado una familia de posibles métodos Runge-Kutta de segundo orden.

Rincón de Sage

Ejemplo de uso del Método de Euler:

video.google.com/googleplayer. swfd=1095449792523736442

Ejemplo narrado del uso del Método Runge-Kutta:

video.google.com/googleplayer.swf=-2281777106160743750

Ejemplo no narrado del uso del método Runge-Kutta:

Archivo:Resolución numérica en Excel, Unnarrated.ppt

Referencias

• “Ecuación diferencial de retardo”, Wolfram MathWorld, Online: 8 de septiembre de 2006. Disponible http://mathworld.wolfram.com/DelayDifferentialEquation.html
• Chapra, Steven C. y Canale, Raymond P. “Métodos numéricos para ingenieros”, Nueva York: McGraw-Hill.
• Franklin, Gene F. y col. “Control de retroalimentación de sistemas dinámicos”, Addison-Wesley Publishing Company.
• R. Inglaterra. “Estimaciones de error para soluciones tipo Runge-Kutta a sistemas de ecuaciones diferenciales ordinarias”, Departamento de Investigación y Desarrollo, Pressed Steel Fisher Ltd., Cowley, Oxford, Reino Unido. Octubre de 1968.
• Call, Dickson H. y Reeves, Roy F. “Estimación de errores en los procedimientos de Runge Kutta”, ACM, Nueva York, NY, EUA. Septiembre de 1958.