9.1: Construcción de diagramas de bloques- Visualización de mediciones de control

Última actualización
Guardar como PDF

Page ID: 85572

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A menudo es conveniente expresar un sistema de control con un diagrama de bloques. Estos diagramas ayudan a visualizar las relaciones entre cada parte del sistema de control (Figura$\PageIndex{1}$).

Figura$\PageIndex{1}$: Diagrama de bloques que representa un sistema de control.

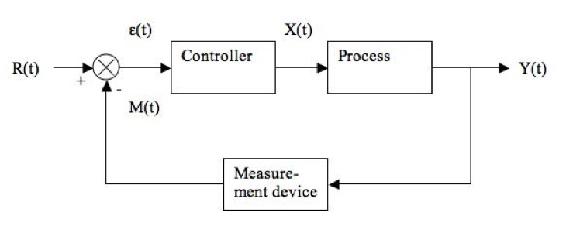
El sistema de control mostrado se denomina sistema de bucle cerrado o sistema de retroalimentación porque el valor medido de la variable controlada se devuelve o “retroalimenta” al comparador. En el comparador la variable controlada se compara con el valor o punto de ajuste deseado. Si hay alguna diferencia entre la variable medida y el punto de ajuste, se genera un error. Este error ingresa a un controlador, que a su vez ajusta el elemento de control final para devolver la variable controlada al punto de ajuste [1].

R (t) = “punto de ajuste”, es sinónimo del valor deseado de la variable controlada
ε (t) = error de proceso o comparador
X (t) = variable de proceso
M (t) = variable de medición
Y (t) = variable de salida

El “hat” por encima de la G indica que es un operador (no una simple función) y puede incluir integración y diferenciación. Así, no se puede dividir por a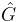 sombrero G , sino que hay que multiplicar ambos lados por su inversa 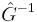$sombrero G^ {-1}$ (ver más abajo). Esta es una representación más general que forma la transformación estándar de Laplace; aquí no es necesario que los operadores sean lineales.

A partir del diagrama de bloques se pueden construir las ecuaciones para un sistema. Defina lo siguiente:

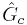=Operador del controlador
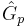=Operador de proceso
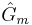=Operador de retardo de medición

Las ecuaciones para el sistema en la Figura$\PageIndex{1}$ se dan a continuación. Tenga en cuenta que estas ecuaciones siempre se escriben como “la salida es igual al operador aplicado a la entrada”.

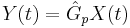
Proceso: $(t) =\ hat G_ {p} X (t)$
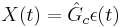
Controlador: $(t) =\ hat G_ {c}\ épsilon (t)$
Comparador: ε (t) = R (t) − M (t)
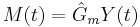
Retraso de medición: $M (t) =\ hat G_ {m} Y (t)$

Típicamente para trazar la respuesta del controlador$Y(t)$,, es necesario resolver estas ecuaciones para obtener una sola ecuación para$Y(t)$. Esto se puede hacer enchufando primero la ecuación de retardo de medición en la ecuación del compartidor, o.

\[\epsilon(t)=R(t)-\hat{G}_{m} Y(t).\nonumber \]

Esta ecuación se puede poner en la ecuación del controlador, o

\[X(t)=\hat{G}_{c}\left[R(t)-G_{m} Y(t)\right].\nonumber \]

Finalmente, la ecuación para se$Y(t)$ puede obtener poniendo la ecuación anterior en la ecuación para el proceso, o

\[Y(t)=\hat{G}_{p} \hat{G}_{c}\left[R(t)-\hat{G}_{m} Y(t)\right].\nonumber \]

Frecuentemente tenemos una ecuación diferencial para$X(t)$ en términos de derivados de$Y(t)$ por lo que escribimos

\[X(t)=\hat{G}_{p}^{-1} Y(t)\nonumber \]

lo que implica la forma de la ecuación general

\[\hat{G}_{p}^{-1} Y(t)=\hat{G}_{c}\left[R(t)-G_{m} Y(t)\right]\nonumber \]

Si se conocen los operadores de proceso, controlador y retardo de medición, se$Y(t)$ puede trazar y se puede observar la respuesta del sistema (es decir, usando Mathematica).

Es decir, tenemos

$Y(t)=\hat{G}_{p} X(t)$
$X(t)=\hat{G}_{c} \epsilon(t)]$
$\epsilon(t)=R(t)-M(t)$
$M(t)=\hat{G}_{m} Y(t)$
$\hat{G}_{p}^{-1} Y(t)=\hat{G}_{c}\left[R(t)-G_{m} Y(t)\right]$

Suponga que no hay retraso de medición:

\[\hat{G}_{m}=1\nonumber \]

Asumir sistema de primer orden:

\[\hat{G}_{p}^{-1}=\frac{1}{K_{p}}\left(\tau_{p} \frac{d}{d t}+1\right)\nonumber \]

Supongamos controlador PI:

\[\hat{G}_{c}^{-1}=K_{c}+\frac{K_{c}}{\tau_{I}} \int_{0}^{t} d t\nonumber \]

Sustituir las ecuaciones (2) y (3) en (5) da:

\[\frac{1}{K_{p}}\left(\tau_{p} \frac{d}{d t} \quad 1\right) Y(t)=\left(K_{z}, \frac{K_{e}}{_{\eta_{1}}} \int_{0}^{t} a t\right) c(t)-\left(K_{z} | \frac{K_{c}}{_{7_{1}}} \int_{0}^{t} d t\right)\{H(t) \quad Y(t)\nonumber \]

Simplificar aún más da:

\[\tau_{p} Y^{\prime}(t)+Y(t)=K_{c}(R(t)-Y(t))+\frac{K_{c}}{\tau_{I}}(R(t)-Y(t))\nonumber \]

Diferenciar la ecuación anterior da:

\[\tau_{p} Y^{\prime \prime}(t)+Y^{\prime}(t)=K_{c} R^{\prime}(t)-K_{c} Y^{\prime}(t)+\frac{K_{c}}{\tau_{I}} R(t)-\frac{K_{c}}{\tau_{I}} Y(t)\nonumber \]

Reordenando la ecuación anterior:

\[\tau_{p} Y^{\prime \prime}(t)+\left(1+K_{c}\right) Y^{\prime}(t)+\frac{K_{c}}{\tau_{I}} Y(t)=K_{c} R^{\prime}(t)+\frac{K_{c}}{\tau_{I}} R(t)\nonumber \]
Multiply the above equation by 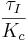$\frac{\tau_{I}}{K_{c}}$ to eliminate the co-efficient of $Y'(t)$ gives:

\[\frac{\tau_{I} \tau_{p}}{K_{c}} Y^{\prime \prime}(t)+\tau_{I} \frac{1+K_{c}}{K_{c}} Y^{\prime}(t)+Y(t)=\tau_{I} R^{\prime}(t)+R(t)\nonumber \]

Referencias

Coughanowr, D.R. y S.E. LeBlanc (2009). Análisis Y Control De Sistemas De Procesos. Tercera Edición. Mc-Graw Hill.