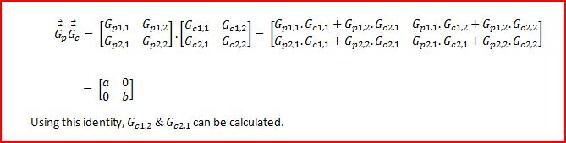12.5: Comprensión del control MIMO mediante la interacción de dos tanques
- Page ID
- 85337
Hemos estado familiarizados con los modelos de tanque de sobretensión simple manipulado por proceso de primer orden y dos tanques en serie manipulados por proceso de segundo orden, los cuales son ejemplos típicos de control de entrada única y salida única (SISO). Sin embargo, en los procesos químicos reales, siempre hay interaciones entre los reactores. En la siguiente página se discutirá el modelo de dos tanques tomando en consideración la interacción entre los dos tanques. Para manipular este modelo, necesitamos usar el control Multiple Input Multiple Output (MIMO), lo que agregará más complejidad en la comprensión del proceso general.
Modelo de interacción de dos tanques
La siguiente figura, Figura 1, demuestra cómo funciona el modelo de dos tanques para interactuar entre sí. De la Figura 1, podemos ver que la entrada de Tank1, x1, no sólo afecta el nivel en Tank1, sino que también afecta al de Tank2. Lo mismo va para la entrada de Tank2, x2. Utilizamos la resistencia, R3, para dar cuenta de la interacción entre los dos tanques.
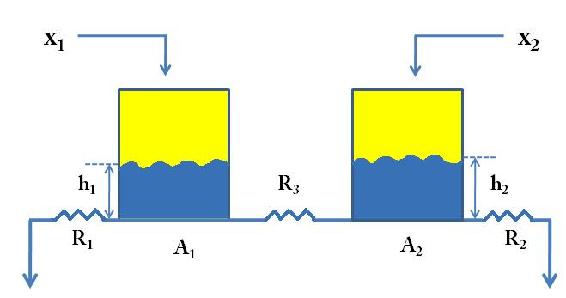
En la figura anterior,
- \(x_1\)= Entrada de Tank1
- \(x_2\)= Entrada de Tank2
- \(A_1\)= Área de sección transversal de Tank1
- \(A_2\)= Área de sección transversal de Tank2
- \(h_1\)= Nivel de Tank1
- \(h_2\)= Nivel de Tank2
- \(R_1\)= Resistencia de Tank1
- \(R_2\)= Resistencia del Tank2
- \(R_3\)= Resistencia a la interacción
Ecuaciones matemáticas para el proceso
Ahora, derivaremos las ecuaciones matemáticas para describir el proceso, ahora asumimos que la dirección del flujo va de Tank1 a Tank2:
Para empezar, escribimos la ecuación gobernante para cada uno de los tanques, tomando en consideración el término de interacción:
\[A_{1} \dfrac{d h_{1}}{d t}=x_{1}-\dfrac{h_{1}}{R_{1}} d t-\dfrac{\left(h_{1}-h_{2}\right)}{R_{3}}=x_{1}+h_{1}\left(-\dfrac{1}{R_{1}}-\dfrac{1}{R_{3}}\right)+h_{2}\left(\dfrac{1}{R_{3}}\right) \nonumber \]
\[A_{2} \dfrac{d h_{2}}{d t}=x_{2}-\dfrac{h_{2}}{R_{2}} d t+\dfrac{\left(h_{1}-h_{2}\right)}{R_{3}}=x_{2}+h_{2}\left(-\dfrac{1}{R_{2}}-\dfrac{1}{R_{3}}\right)+h_{1}\left(\dfrac{1}{R_{3}}\right) \nonumber \]
En estado estacionario, las derivadas del tiempo, es decir, el lado izquierdo de las ecuaciones anteriores, van a cero:
\[0=x_{1}(0)+h_{1}(0)\left(-\dfrac{1}{R_{1}}-\dfrac{1}{R_{3}}\right)+h_{2}(0)\left(\dfrac{1}{R_{3}}\right) \nonumber \]
\[0=x_{2}(0)+h_{1}(0)\left(\dfrac{1}{R_{3}}-\dfrac{1}{R_{3}}\right)+h_{2}(0)\left(-\dfrac{1}{R_{2}}-\dfrac{1}{R_{3}}\right) \nonumber \]
Ahora, definimos las variables de desviación de la siguiente manera:
- \(X_1 = x_1 − x_1(0)\)
- \(Y_1 = h_1 − h_1(0)\)
- \(X_2 = x_2 − x_2(0)\)
- \(Y_2 = h_2 − h_2(0)\)
Establecer\(y_1=h_1\) y\(y_2=h_2\), podemos obtener las siguientes ecuaciones:
\[A_{1} \dfrac{d y_{1}}{d t}=\dfrac{x_{1}}{A_{1}}+y_{1}\left(-\dfrac{1}{A_{1} R_{1}}-\dfrac{1}{A_{1} R_{3}}\right)+y_{2}\left(\dfrac{1}{A_{1} R_{3}}\right) \nonumber \]
\[A_{2} \dfrac{d y_{2}}{d t}=\dfrac{x_{2}}{A_{1}}+y_{1}\left(\dfrac{1}{A_{2} R_{3}}\right)+y_{2}\left(-\dfrac{1}{A_{2} R_{2}}-\dfrac{1}{A_{2} R_{3}}\right) \nonumber \]
Será más general si escribimos las ecuaciones anteriores en una forma de Matriz:
\ [\ left [\ begin {array} {c}
\ dot {y} _ {1}\
\ dot {y} _ {2}
\ end {array}\ right] =\ left [\ begin {array} {cc}
\ dfrac {1} {A_ {1}} & 0\\
0 &\ dfrac {1} {A_ {2}}
\ end {array} derecha]\ left [\ begin {array} {c}
x_ {1}\\
x_ {2}
\ end {array}\ derecha] +\ izquierda [\ begin {array} {cc}
-\ dfrac {1} {A_ {1} R_ {1}} -\ dfrac {1} {A_ {1} R_ {2}} &\ dfrac {1} {A_ {1} R_ {3}}\
\ dfrac {1} {A_ {2} R_ {3}} & -\ dfrac {1} {A_ {2} R_ {2}} -\ dfrac {1} {A_ {2} R_ {3}}
\ end {array}\ derecha]\ izquierda [\ begin {array} {c}
y_ {1}\\
y_ {2}
\ end {array}\ derecha]\ nonumber\]
Podemos representar la ecuación anterior usando la siguiente ecuación:
\ [\ begin {array} {c}
\ vec {y} =\ overrightarrow {\ vec {B}}\ vec {x} +\ overrightarrow {\ vec {A}}\ vec {y}\
\ vec {y} -\ vec {A}\ vec {y} =\ overrightarrow {\ vec {B}}\ vec {x}\
\ vec {x} =\ izquierda (\ vec {B} ^ {-1}\ derecha)\ izquierda (\ dfrac {\ parcial} {\ parcial} -\ overrightarrow {\ vec {A}}\ derecha)\ vec {y} =\ overrightarrow {\ vec {G} _ {p}} ^ {-1}\ vec {y}
\ end {array}\ nonumber\]
Invertir la ecuación anterior:
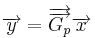
Ahora, establece
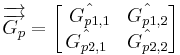
Obtenemos la siguiente ecuación:
\ [\ left [\ begin {array} {c}
y_ {1}\\
y_ {2}
\ end {array}\ right] =\ left [\ begin {array} {cc}
\ hat {G} _ {p 1,1} &\ hat {G} _ {p 1,2}\
\ hat {G} _ {p 2,1} &\ hat {G} _ {p 2,2}
\ end {array}\ derecha]\ izquierda [\ begin {array} {c}
x_ {1} \\
x_ {2}
\ end {array}\ derecha]\]
Diagrama de control
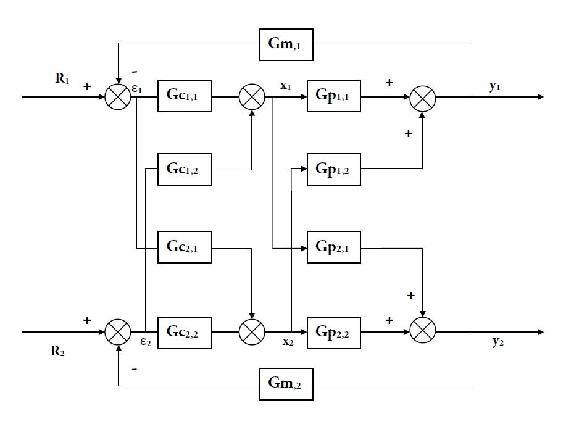
Desacoplar el proceso