13.1: Estadísticas básicas: media, mediana, promedio, desviación estándar, puntuaciones z y valor p

La estadística es un campo de las matemáticas que pertenece al análisis de datos. Se pueden aplicar métodos estadísticos y ecuaciones a un conjunto de datos para analizar e interpretar resultados, explicar variaciones en los datos o predecir datos futuros. Algunos ejemplos de información estadística que podemos calcular son:

• Valor promedio (media)
• Valor que ocurre con mayor frecuencia (modo)
• En promedio, cuánto se desvía cada medición de la media (desviación estándar de la media)
• Rango de valores sobre los cuales se produce el conjunto de datos (rango), y
• Punto medio entre el valor más bajo y más alto del conjunto (mediana)

La estadística es importante en el campo de la ingeniería ya que proporciona herramientas para analizar los datos recopilados. Por ejemplo, un ingeniero químico puede desear analizar las mediciones de temperatura de un tanque de mezcla. Se pueden usar métodos estadísticos para determinar qué tan confiables y reproducibles son las mediciones de temperatura, cuánto varía la temperatura dentro del conjunto de datos, qué temperaturas futuras del tanque pueden ser y qué tan seguro puede estar el ingeniero en las mediciones de temperatura realizadas. Este artículo cubrirá las funciones estadísticas básicas de media, mediana, modo, desviación estándar de la media, promedios ponderados y desviaciones estándar, coeficientes de correlación, puntuaciones z y valores p.

¿Qué es una Estadística?

En la mente de un estadístico, el mundo consiste en poblaciones y muestras. Un ejemplo de población son todos los estudiantes de séptimo grado en Estados Unidos. Un ejemplo relacionado de una muestra sería un grupo de estudiantes de séptimo grado en Estados Unidos. En este ejemplo en particular, a un administrador federal de atención médica le gustaría saber el peso promedio de los estudiantes de séptimo grado y cómo se compara ese con otros países. Desafortunadamente, es demasiado caro medir el peso de cada alumno de séptimo grado en Estados Unidos. En cambio, se pueden usar metodologías estadísticas para estimar el peso promedio de los estudiantes de séptimo grado en los Estados Unidos midiendo los pesos de una muestra (o múltiples muestras) de estudiantes de séptimo grado.

Los parámetros son para las poblaciones como los estadísticos para las muestras.

Un parámetro es una propiedad de una población. Como se ilustra en el ejemplo anterior, la mayoría de las veces es inviable medir directamente un parámetro poblacional. En su lugar se debe tomar una muestra y se calcula el estadístico para la muestra. Esta estadística puede ser utilizada para estimar el parámetro poblacional. (Una rama de la estadística conocida como Estadística Inferencial implica el uso de muestras para inferir información sobre una población.) En el ejemplo sobre el parámetro poblacional se encuentra el peso promedio de todos los estudiantes de 7º grado en Estados Unidos y el estadístico muestral es el peso promedio de un grupo de estudiantes de 7º grado.

Un gran número de técnicas de inferencia estadística requieren que las muestras sean una sola muestra aleatoria y se reúna de forma independiente. En definitiva, esto permite que las estadísticas sean tratadas como variables aleatorias. Una discusión en profundidad sobre estas consecuencias está fuera del alcance de este texto. También es importante señalar que las estadísticas pueden ser defectuosas debido a la gran varianza, sesgo, inconsistencia y otros errores que puedan surgir durante el muestreo. Siempre que se realiza una revisión excesiva del análisis estadístico, un ojo escéptico siempre es valioso.

Las estadísticas toman muchas formas. Ejemplos de estadísticas se pueden ver a continuación.

Estadísticas Básicas

Al realizar análisis estadísticos sobre un conjunto de datos, la media, la mediana, el modo y la desviación estándar son todos valores útiles para calcular. La media, mediana y modo son todas estimaciones de dónde está el “medio” de un conjunto de datos. Estos valores son útiles a la hora de crear grupos o bins para organizar conjuntos de datos más grandes. La desviación estándar es la distancia promedio entre los datos reales y la media.

Media y Promedio Ponderado

La media (también conocida como promedio), se obtiene dividiendo la suma de los valores observados por el número de observaciones, n. Aunque los puntos de datos caen por encima, por debajo o en la media, se puede considerar una buena estimación para predecir puntos de datos posteriores. La fórmula para la media se da a continuación como Ecuación\ ref {1}. La sintaxis de excel para la media es PROMEDIO (celda inicial: celda final).

\[\bar{X}=\frac{\sum_{i=1}^{i=n} X_{i}}{n} \label{1} \]

Sin embargo, la ecuación (1) sólo se puede utilizar cuando el error asociado a cada medición es el mismo o desconocido. De lo contrario, el promedio ponderado, que incorpora la desviación estándar, debe calcularse utilizando la ecuación (2) a continuación.

\[X_{w a v}=\frac{\sum w_{i} x_{i}}{\sum w_{i}} \label{2} \]

donde\[w_{i}=\frac{1}{\sigma_{i}^{2}}\nonumber \] y\(x_i\) es el valor de los datos.

Mediana

La mediana es el valor medio de un conjunto de datos que contienen un número impar de valores, o el promedio de los dos valores medios de un conjunto de datos con un número par de valores. La mediana es especialmente útil cuando se separan los datos en dos bins de igual tamaño. La sintaxis de excel para encontrar la mediana es MEDIAN (celda inicial: celda final).

Modo

El modo de un conjunto de datos es el valor que ocurre con mayor frecuencia. La sintaxis de excel para el modo es MODE (celda inicial: celda final).

Consideraciones

Ahora que hemos discutido algunas formas diferentes en las que puede describir un conjunto de datos, tal vez se esté preguntando cuándo usar cada forma. Bueno, si todos los puntos de datos están relativamente cercanos entre sí, el promedio te da una buena idea de a qué están más cerca los puntos. Si por otro lado, casi todos los puntos caen cerca de uno, o de un grupo de valores cercanos, pero ocasionalmente se puede ver un valor que difiere mucho, entonces el modo podría ser más preciso para describir este sistema, mientras que la media incorporaría los datos periféricos ocasionales. La mediana es útil si estás interesado en el rango de valores en los que tu sistema podría estar operando. La mitad de los valores deben estar por encima y la mitad de los valores deben estar por debajo, así que tienes una idea de dónde está el punto medio de operación.

Desviación estándar y desviación estándar ponderada

La desviación estándar da una idea de lo cerca que está todo el conjunto de datos al valor promedio. Los conjuntos de datos con una pequeña desviación estándar tienen datos muy agrupados y precisos. Los conjuntos de datos con grandes desviaciones estándar tienen datos distribuidos en una amplia gama de valores. La fórmula para la desviación estándar se da a continuación como Ecuación\ ref {3}. La sintaxis de excel para la desviación estándar es STDEV (celda inicial: celda final).

\[\sigma=\sqrt{\frac{1}{n-1} \sum_{i=1}^{i=n}\left(X_{i}-\bar{X}\right)^{2}} \label{3} \]

Nota al margen: Estimación de sesgo de varianza poblacional

La desviación estándar (raíz cuadrada de varianza) de una muestra puede ser utilizada para estimar la varianza verdadera de una población. La ecuación\ ref {3} anterior es una estimación imparcial de la varianza poblacional. La ecuación\ ref {3.1} es otro método común para calcular la desviación estándar de la muestra, aunque es una estimación de sesgo. Aunque la estimación es sesgada, es ventajosa en ciertas situaciones porque la estimación tiene una varianza menor. (Esto se relaciona con la compensación de sesgo-varianza para los estimadores).

\[\sigma_{n}=\sqrt{\frac{1}{n} \sum_{i=1}^{i=n}\left(X_{i}-\bar{X}\right)^{2}} \label{3.1} \]

Cuando se calculan los valores de desviación estándar asociados con promedios ponderados, se debe usar la Ecuación\ ref {4} a continuación.

\[\sigma_{w a v}=\frac{1}{\sqrt{\sum w_{i}}} \label{4} \]

La distribución muestral y la desviación estándar de la media

Los parámetros poblacionales siguen todo tipo de distribuciones, algunos son normales, otros están sesgados como la distribución F y algunos ni siquiera tienen momentos definidos (media, varianza, etc.) como la distribución de Chaucy. Sin embargo, muchas metodologías estadísticas, como una prueba z (discutida más adelante en este artículo), se basan en la distribución normal. ¿Cómo funciona esto? La mayoría de los datos de muestra no se distribuyen normalmente.

Esto pone de manifiesto un malentendido común de aquellos nuevos en la inferencia estadística. La distribución del parámetro poblacional de interés y la distribución muestral no son las mismas. Distribución de muestreo?!? ¿Qué es eso?

Imagine que una ingeniería está estimando el peso medio de los widgets producidos en un lote grande. El ingeniero mide el peso de N widgets y calcula la media. Hasta el momento, se ha tomado una muestra. Luego, el ingeniero toma otra muestra, y otra y otra continúa hasta que se ha recopilado un número muy mayor de muestras y, por lo tanto, un mayor número de pesos medios de muestra (supongamos que el lote de widgets del que se muestrean es casi infinito por simplicidad). El ingeniero ha generado una distribución de muestras.

Como sugiere el nombre, una distribución muestral es simplemente una distribución de un estadístico particular (calculado para una muestra con un tamaño establecido) para una población particular. En este ejemplo, el estadístico es el peso promedio del widget y el tamaño de la muestra es N. Si el ingeniero fuera a trazar un histograma de los pesos medios de widget, él/ella vería una distribución en forma de campana. Esto se debe a que el Teorema del Límite Central garantiza que a medida que el tamaño de la muestra se acerca al infinito, las distribuciones muestrales de estadísticas calculadas a partir de dichas muestras se acercan a

Convenientemente, existe una relación entre la desviación estándar de la muestra (σ) y la desviación estándar de la distribución muestral (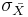también conocida como la desviación estándar de la media o desviación estándar del error). Esta relación se muestra en la Ecuación\ ref {5} a continuación:

\[\sigma_{\bar{X}}=\frac{\sigma_{X}}{\sqrt{N}} \label{5} \]

Una característica importante de la desviación estándar de la media,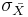 es el factor 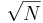en el denominador. A medida que aumenta el tamaño de la muestra, la desviación estándar de la media disminuye mientras que la desviación estándar, σ no cambia apreciablemente.

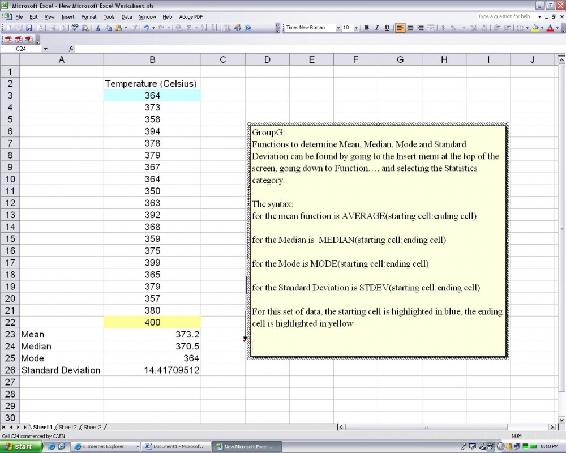
Microsoft Excel ha incorporado funciones para analizar un conjunto de datos para todos estos valores. Por favor, vea la captura de pantalla a continuación de cómo se podría analizar un conjunto de datos usando Excel para recuperar estos valores.

Ejemplo a Mano

Obtienes los siguientes puntos de datos y quieres analizarlos usando métodos estadísticos básicos. {1,2,2,3,5}

Calcular el promedio: Contar el número de puntos de datos a obtener\(n = 5\)

\[mean =\frac{1+2+2+3+5}{5}=2.6\nonumber \]

Obtener el modo: Ya sea usando la sintaxis excel del tutorial anterior, o mirando el conjunto de datos, uno puede notar que hay dos 2's, y no hay múltiplos de otros puntos de datos, lo que significa que el 2 es el modo.

Obtener la mediana: Conociendo el n=5, el punto medio debe ser el tercer número (medio) en una lista de los puntos de datos listados en orden ascendente o descendente. Viendo como los números ya están listados en orden ascendente, el tercer número es 2, por lo que la mediana es 2.

Calcular la desviación estándar: Usando la ecuación\ ref {3},

\[\sigma =\sqrt{\frac{1}{5-1} \left( 1 - 2.6 \right)^{2} + \left( 2 - 2.6\right)^{2} + \left(2 - 2.6\right)^{2} + \left(3 - 2.6\right)^{2} + \left(5 - 2.6\right)^{2}} =1.52\nonumber \]

Ejemplo a Mano (Ponderado)

Tres estudiantes de la Universidad de Michigan midieron la asistencia a la misma clase de Controles de Procesos varias veces. Sus tres respuestas fueron (todas en unidades personas):

• Alumno 1: A = 100 ± 3
• Estudiante 2: A = 105 ± 4
• Estudiante 3: A = 102 ± 2

¿Cuál es la mejor estimación para la asistencia A?

,,,

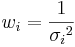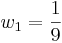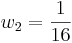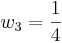
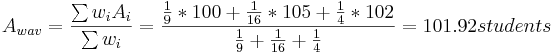
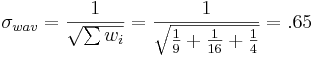
Por lo tanto,

\[A = 101.92 ± 0.65\, students \nonumber \]

Distribución Gaussiana

La distribución gaussiana, también conocida como distribución normal, está representada por la siguiente función de densidad de probabilidad:

\[P D F_{\mu, \sigma}(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}\nonumber \]

donde μ es la media y σ es la desviación estándar de un conjunto de datos muy grande. La distribución gaussiana es una curva en forma de campana, simétrica sobre el valor medio. A continuación se muestra un ejemplo de una distribución gaussiana.

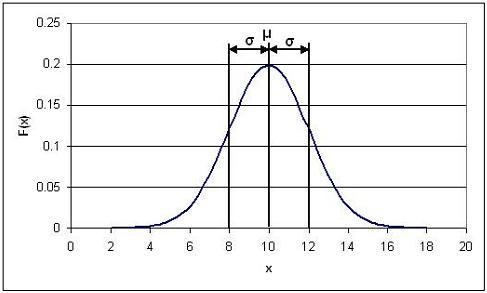
En este ejemplo específico, μ = 10 y σ = 2.

Las funciones de densidad de probabilidad representan la dispersión del conjunto de datos. Integrar la función de algún valor x a x + a donde a es algún valor real da la probabilidad de que un valor caiga dentro de ese rango. La integral total de la función de densidad de probabilidad es 1, ya que cada valor caerá dentro del rango total. El área sombreada en la imagen de abajo da la probabilidad de que un valor caiga entre 8 y 10, y está representado por la expresión:

La distribución gaussiana es importante para el control estadístico de calidad, seis sigma e ingeniería de calidad en general. Para más información consulta ¿Qué es 6 sigma?.

Función de error

También se puede estimar una distribución normal o gaussiana con una función de error como se muestra en la siguiente ecuación.

\[P(8 \leq x \leq 10)=\int_{8}^{10} \frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} d x=\operatorname{erf}(t)\nonumber \]

Aquí, erf (t) se llama “función de error” por su papel en la teoría de la variable aleatoria normal. La gráfica siguiente muestra la probabilidad de que un punto de datos se encuentre dentro de t*σ de la media.

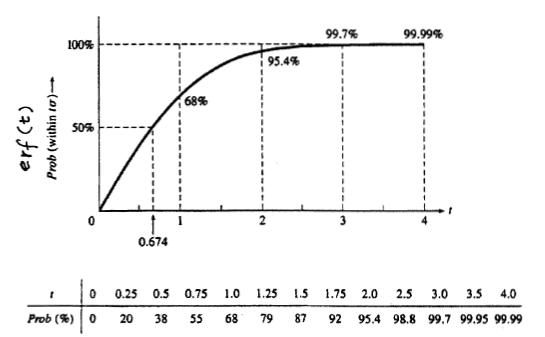
Por ejemplo, si querías saber la probabilidad de que un punto caiga dentro de 2 desviaciones estándar de la media puedes mirar fácilmente esta tabla y encontrar que es de 95.4%. Esta tabla es muy útil para buscar rápidamente qué probabilidad un valor caerá en x desviaciones estándar de la media.

Coeficiente de correlación (valor r)

El coeficiente de correlación lineal es una prueba que se puede utilizar para ver si existe una relación lineal entre dos variables. Por ejemplo, es útil si se compara una ecuación lineal con puntos experimentales. Se utiliza la siguiente ecuación:

\[r=\frac{\sum\left(X_{i}-X_{\text {mean}}\right)\left(Y_{i}-Y_{\text {mean}}\right)}{\sqrt{\sum\left(X_{i}-X_{\text {mean}}\right)^{2}} \sqrt{\sum\left(Y_{i}-Y_{\text {mean}}\right)^{2}}}\nonumber \]

El rango de r es de -1 a 1. Si el valor r es cercano a -1 entonces la relación se considera anticorrelacionada, o tiene una pendiente negativa. Si el valor es cercano a 1 entonces la relación se considera correlacionada, o tener una pendiente positiva. A medida que el valor r se desvía de cualquiera de estos valores y se acerca a cero, se considera que los puntos se vuelven menos correlacionados y eventualmente no están correlacionados.

También hay tablas de probabilidad que se pueden utilizar para mostrar la significante de linealidad en función del número de mediciones. Si la probabilidad es inferior al 5% la correlación se considera significativa.

Regresión lineal

El coeficiente de correlación se utiliza para determinar si existe o no una correlación dentro de su conjunto de datos. Una vez establecida una correlación, la relación real se puede determinar mediante la realización de una regresión lineal. El primer paso para realizar una regresión lineal es calcular la pendiente e intercepción:

\[\mathit{Slope} = \frac{n\sum_i X_iY_i -\sum_i X_i \sum_j Y_j }

ParseError: EOF expected (click for details)

Callstack:
    at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/13:_Estadísticas_y_antecedentes_probabilísticos/13.01:_Estadísticas_básicas), /content/body/div[2]/div[12]/p[2]/span/span, line 1, column 2

\nonumber \]

\[\mathrm{Intercept} = \frac{(\sum_i X_i^2)\sum_i(Y_i)-\sum_i X_i\sum_i X_iY_i }

ParseError: invalid ArgList (click for details)

Callstack:
    at (Ingenieria/Ingeniería_Industrial_y_de_Sistemas/Libro:_Dinámica_y_Controles_de_Procesos_Químicos_(Woolf)/13:_Estadísticas_y_antecedentes_probabilísticos/13.01:_Estadísticas_básicas), /content/body/div[2]/div[12]/p[3]/span/span, line 1, column 3

\nonumber \]

Una vez que se calcula la pendiente y la intersección, es necesario aplicar la incertidumbre dentro de la regresión lineal. Para calcular la incertidumbre, es necesario calcular el error estándar para la línea de regresión.

\[S=\sqrt{\frac{1}{n-2}\left(\left(\sum_{i} Y_{i}^{2}\right)-\text { intercept } \sum Y_{i}-\operatorname{slope}\left(\sum_{i} Y_{i} X_{i}\right)\right)}\nonumber \]

El error estándar se puede usar para encontrar el error específico asociado con la pendiente e interceptar:

\[S_{\text {slope }}=S \sqrt{\frac{n}{n \sum_{i} X_{i}^{2}-\left(\sum_{i} X_{i}\right)^{2}}}\nonumber \]

\[S_{\text {intercept }}=S \sqrt{\frac{\sum\left(X_{i}^{2}\right)}{n\left(\sum X_{i}^{2}\right)-\left(\sum_{i} X_{i} Y_{i}\right)^{2}}}\nonumber \]

Una vez que se determina el error asociado con la pendiente y la intercepción, se debe aplicar un intervalo de confianza al error. Un intervalo de confianza indica la probabilidad de que cualquier punto de datos dado, en el conjunto de puntos de datos, caiga dentro de los límites de la incertidumbre.

\[\beta=slope\pm\Delta slope\simeq slope\pm t^*S_{slope} \nonumber \]

\[\alpha=intercept\pm\Delta intercept\simeq intercept\pm t^*S_{intercept} \nonumber \]

Ahora que se ha calculado la pendiente, la intercepción y sus respectivas incertidumbres, se puede determinar la ecuación para la regresión lineal.

\[Y = βX + α\nonumber \]

Puntajes Z

Un puntaje z (también conocido como valor z, puntaje estándar o puntaje normal) es una medida de la divergencia de un resultado experimental individual a partir del resultado más probable, la media. Z se expresa en términos del número de desviaciones estándar del valor medio.

\[z=\frac{X-\mu}{\sigma} \label{6} \]

• X = ExperimentalValue
• μ = Media
• σ = desviación estándar

Puntajes Z asumiendo que la distribución muestral del estadístico de prueba (media en la mayoría de los casos) es normal y transforman la distribución muestral en una distribución normal estándar. Como se explicó anteriormente en la sección sobre distribuciones de muestreo, la desviación estándar de una distribución de muestreo depende del número de muestras. La ecuación (6) se utilizará para comparar los resultados entre sí, mientras que la ecuación (7) se utilizará al realizar inferencia sobre la población.

Siempre que se utilicen puntuaciones z es importante recordar algunas cosas:

• Las puntuaciones Z normalizan la distribución del muestreo para una comparación significativa.
• Las puntuaciones Z requieren una gran cantidad de datos.
• Las puntuaciones Z requieren datos aleatorios independientes.

\[z_{o b s}=\frac{X-\mu}{\frac{\sigma}{\sqrt{n}}} \label{7} \]

• n = SampleNumber

Valor P

Un valor p es un valor estadístico que detalla cuánta evidencia hay para rechazar la explicación más común para el conjunto de datos. Se puede considerar que es la probabilidad de obtener un resultado al menos tan extremo como el observado, dado que la hipótesis nula es cierta. En ingeniería química, el valor p se suele utilizar para analizar las condiciones marginales de un sistema, en cuyo caso el valor p es la probabilidad de que la hipótesis nula sea verdadera.

La hipótesis nula es considerada como el escenario más plausible que puede explicar un conjunto de datos. La hipótesis nula más común es que los datos son completamente aleatorios, que no hay relación entre dos resultados del sistema. Siempre se asume que la hipótesis nula es verdadera a menos que se demuestre lo contrario. Una hipótesis alternativa predice lo contrario de la hipótesis nula y se dice que es cierta si se demuestra que la hipótesis nula es falsa.

El siguiente es un ejemplo de estas dos hipótesis:

4 alumnos que se sentaron en la misma mesa durante un examen obtuvieron puntajes perfectos.

• Hipótesis nula: La falta de desviación de puntaje ocurrió por casualidad.
• Hipótesis alternativa: Hay alguna otra razón por la que todos recibieron la misma puntuación.

Si se encuentra que la hipótesis nula es cierta entonces el Consejo de Honor no necesitará involucrarse. Sin embargo, si se encuentra cierta la hipótesis alternativa, entonces habrá que hacer más estudios para probar esta hipótesis y conocer más sobre la situación.

Como se mencionó anteriormente, el valor p puede ser utilizado para analizar condiciones marginales. En este caso, la hipótesis nula es que no existe relación entre las variables que controlan el conjunto de datos. Por ejemplo:

• El alimento que moquea no tiene impacto en la calidad del producto
• Los puntos en un gráfico de control se dibujan de la misma distribución
• Dos envíos de pienso son estadísticamente iguales

El valor p prueba o desmiente la hipótesis nula en función de su significación. Se dice que un valor p es significativo si es menor que el nivel de significancia, que comúnmente es del 5%, 1% o .1%, dependiendo de qué tan precisos deben ser los datos o estrictos que sean los estándares. Por ejemplo, una compañía de atención médica puede tener un menor nivel de significación porque tiene estándares estrictos. Si el valor p se considera significativo (es menor que el nivel de significancia especificado), la hipótesis nula es falsa y se deben hacer más pruebas para probar la hipótesis alternativa.

Al encontrar el valor p y posteriormente llegar a una conclusión para rechazar la Hipótesis Null o no rechazar la Hipótesis Null, también existe la posibilidad de que se pueda tomar la decisión equivocada. Si la decisión es rechazar la Hipótesis Null y de hecho la Hipótesis Null es verdadera, se ha producido un error tipo 1. La probabilidad de un error tipo uno es la misma que el nivel de significancia, por lo que si el nivel de significancia es del 5%, “la probabilidad de un error tipo 1” es .05 o 5%. Si la decisión es no rechazar la Hipótesis Null y de hecho la Hipótesis Alternativa es cierta, acaba de ocurrir un error de tipo 2. Con respecto al error tipo 2, si la Hipótesis Alternativa es realmente cierta, otra probabilidad que es importante para los investigadores es la de poder detectar esto y rechazar la Hipótesis Null. Esta probabilidad se conoce como la potencia (de la prueba) y se define como 1 - “probabilidad de cometer un error tipo 2".

Si se produce un error en el ejemplo mencionado anteriormente probando si existe una relación entre las variables que controlan el conjunto de datos, ya sea un error tipo 1 o tipo 2 podría llevar a una gran cantidad de producto desperdiciado, o incluso a un proceso salvajemente fuera de control. Por lo tanto, al diseñar los parámetros para las pruebas de hipótesis, los investigadores deben sopesar fuertemente sus opciones de nivel de significancia y potencia de la prueba. La sensibilidad del proceso, el producto y los estándares para el producto pueden ser sensibles al error más pequeño.

Nota Importante Acerca de los Valores P Significativos

Si un valor P es mayor que el nivel de significancia aplicado, y la hipótesis nula no solo debe aceptarse ciegamente. Se deben realizar otras pruebas para determinar la verdadera relación entre las variables que se están probando. Más información sobre este y otros malentendidos relacionados con los valores P se puede encontrar en Valores P: Malentendidos frecuentes.

Cálculo

Hay dos formas de calcular un valor p. El primer método se utiliza cuando se ha calculado la puntuación z. El segundo método se utiliza con el método exacto de Fisher y se utiliza al analizar condiciones marginales.

Primer Método: Z-Score

El método para encontrar el Valor P es en realidad bastante simple. Primero calcule la puntuación z y luego busque su valor p correspondiente usando la tabla normal estándar.

Esta tabla se puede encontrar aquí: Media:GROUP_G_Z-Table.xls

Este valor representa la probabilidad de que los resultados no se produzcan debido a errores aleatorios sino a una diferencia real en los conjuntos de datos.

Para leer la tabla normal estándar, primero busque la fila correspondiente al dígito significativo inicial del valor z en la columna del lado izquierdo de la tabla. Después de ubicar la fila apropiada, muévase a la columna que coincida con el siguiente dígito significativo.

Ejemplo:
Si tu puntuación z = 1.13

Siga las filas hacia abajo hasta 1.1 y luego a través de las columnas hasta 0.03. El valor P es el cuadro resaltado con un valor de 0.87076.

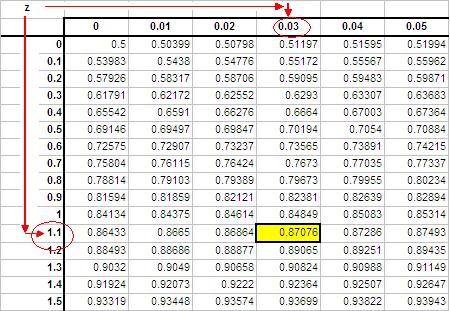
Los valores en la tabla representan el área bajo la curva de distribución normal estándar a la izquierda de la puntuación z.

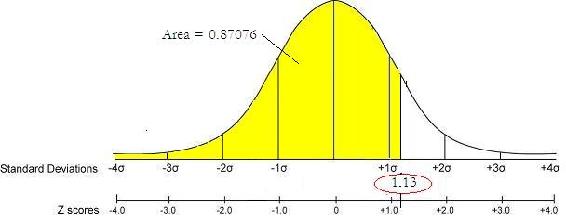
Usando el ejemplo anterior:

Puntaje Z = 1.13, el valor P = 0.87076 se representa gráficamente a continuación.

Segundo Método: Exacto de Fisher

En el caso de analizar condiciones marginales, el valor P se puede encontrar sumando los valores exactos de Fisher para la configuración marginal actual y cada caso más extremo utilizando los mismos marginales. Para información sobre cómo calcular la exacta de Fisher da clic en el siguiente enlace:DISCRETE_DISCRETIONS:_Hypergeometric, _binomial, _and_poisson #Fisher .27s_exact

Prueba de Chi-Cuadrado

Una prueba de Chi-Cuadrado da una estimación sobre la concordancia entre un conjunto de datos observados y un conjunto aleatorio de datos que esperaba que encajaran las mediciones. Dado que los valores observados son continuos, los datos deben dividirse en bins que contienen algunos datos observados cada uno. Los contenedores se pueden elegir para tener algún tipo de separación natural en los datos. Si no existe ninguna de estas divisiones, entonces los intervalos pueden elegirse para ser de igual tamaño o algún otro criterio.

El valor calculado de chi cuadrado puede entonces correlacionarse con una probabilidad usando excel o gráficos publicados. Similar a la exacta de Fisher, si esta probabilidad es mayor a 0.05, la hipótesis nula es verdadera y los datos observados no son significativamente diferentes a los aleatorios.

Cálculo de Chi Cuadrado

El cálculo del Chi cuadrado implica sumar las distancias entre los datos observados y aleatorios. Como esta distancia depende de la magnitud de los valores, se normaliza dividiendo por el valor aleatorio

\[\chi^2 =\sum_{k=1}^N \frac{(observed-random)^2}{random}\nonumber \]

o si el error en el valor observado (sigma) es conocido o puede calcularse:

\[\chi^{2}=\sum_{k=1}^{N}\left(\frac{\text { observed }-\text { theoretical }}{\text { sigma }}\right)^{2}\nonumber \]

Pasos Detallados para Calcular Chi Cuadrado a Mano

Calcular Chi cuadrado es muy simple cuando se define en profundidad, y en forma paso a paso se puede utilizar fácilmente para la estimación de la concordancia entre un conjunto de datos observados y un conjunto aleatorio de datos que esperaba que encajaran las mediciones. Dados los datos:

Paso 1: Encontrar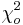

\[\chi_o^2 =\sum_{i} \frac{(y_i-A-Bx_i)^2}{\sigma_{yi}^2}\nonumber \]

Cuando:

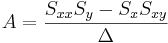
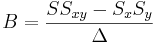
\[\Delta=SS_{xx}-(S_x)^2\,\!\nonumber \]

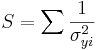
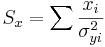
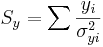
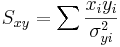
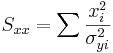
La función de Excel CHITEST (actual_range, expected_range) también calcula el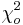 valor. Las dos entradas representan el rango de datos los datos reales y esperados, respectivamente.

Paso 2: Encuentra los Grados de Libertad

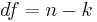
Cuando: df = Grados de Libertad

• n = número de observaciones
• k = el número de restricciones

Paso 3: Encontrar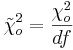

\[\tilde{\chi}_o^2\nonumber \]= el valor establecido de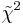 obtenido en un experimento con df grados de libertad

Paso 4: Encuentra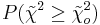 usando Excel o gráficos publicados.

La función de Excel CHIDIST (x, df) proporciona el valor p, donde x es el valor del estadístico chi-cuadrado y df es los grados de libertad. Nota: Excel da solo el valor p y no el valor del estadístico chi-cuadrado.

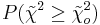= la probabilidad de obtener un valor de 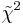eso es tan grande como el establecido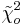

Paso 5: Comparar la probabilidad con el nivel de significancia (es decir, 5% o 0.05), si esta probabilidad es mayor a 0.05, la hipótesis nula es verdadera y los datos observados no son significativamente diferentes a los aleatorios. Una probabilidad menor a 0.05 es un indicador de independencia y una diferencia significativa con respecto al azar.

Prueba de Chi Cuadrado versus Exacto de Fisher

• Para tamaños de muestra pequeños, la Prueba de Chi Cuadrado no siempre producirá una probabilidad precisa. No obstante, para un nulo aleatorio, el exacto de Fisher, como su nombre, siempre dará un resultado exacto.

• Chi Cuadrado no será correcto cuando:

1. se están utilizando menos de 20 muestras
2. si un número esperado es 5 o inferior y hay entre 20 y 40 muestras

• Para tablas de contingencia grandes y distribuciones esperadas que no son aleatorias, el valor p de Fisher's Exact puede ser difícil de calcular, y la Prueba Chi Cuadrada será más fácil de llevar a cabo.

Binning en Chi Cuadrado y Pruebas Exactas de Fisher

Al realizar diversos análisis estadísticos encontrará que las pruebas exactas de Chi-cuadrado y Fisher pueden requerir binning, mientras que ANOVA no. Aunque no hay una opción óptima para el número de bins (k), existen varias fórmulas que se pueden utilizar para calcular este número en función del tamaño de la muestra (N). Un ejemplo de este tipo se enumera a continuación:

\[k = 1 + log_2N \nonumber \nonumber \]

Otro método consiste en agrupar los datos en intervalos de igual probabilidad o igual ancho. El primer enfoque en el que los datos se agrupan en intervalos de igual probabilidad es generalmente más aceptable ya que maneja los datos de pico mucho mejor. Como estipulación, cada contenedor debe contener al menos 5 o más puntos de datos, por lo que a veces es necesario unir ciertos bins adyacentes para que se cumpla esta condición. Identificar el número de los bins a usar es importante, pero es aún más importante poder anotar qué situaciones requieren binning. Algunas situaciones de Chi-cuadrado y exactas de Fisher se enumeran a continuación:

• Análisis de una variable continua:

Esta situación requerirá binning. La idea es dividir el rango de valores de la variable en intervalos más pequeños llamados bins.

• Análisis de una variable discreta:

El binning es innecesario en esta situación. Por ejemplo, un lanzamiento de moneda dará como resultado dos posibles resultados: cabeza o cola. Al arrojar diez monedas, simplemente puedes contar el número de veces que recibiste cada resultado posible. Este enfoque es similar a elegir dos contenedores, cada uno de los cuales contiene un resultado posible.

• Ejemplos de cuándo bin, y cuando no bin:

• Tienes veinte mediciones de la temperatura dentro de un reactor: como la temperatura es una variable continua, debes bin en este caso. Un enfoque podría ser determinar la media (X) y la desviación estándar (σ) y agrupar los datos de temperatura en cuatro bins: T < X — σ, X — σ < T < X, X < T < X + σ, T > X + σ
• Tiene veinte puntos de datos del ajuste del calentador del reactor (alto, medio, bajo): dado que el ajuste del calentador es discreto, no debe bin en este caso.

Ejemplo\(\PageIndex{1}\)

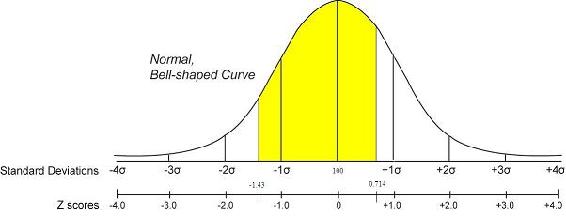
Digamos que tenemos un reactor con una lectura de presión media de 100 y desviación estándar de 7 psig. Calcular la probabilidad de medir una presión entre 90 y 105 psig.

Solución

Para ello haremos uso de las puntuaciones z.

\[\operatorname{Pr}(a \leq z \leq b)=F(b)-F(a)=F\left(\frac{b-\mu}{\sigma}\right)-F\left(\frac{a-\mu}{\sigma}\right)\nonumber \]

donde\(a\) está el límite inferior y\(b\) es el límite superior

Sustitución de la ecuación de transformación z (3)

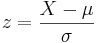
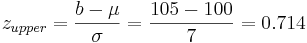
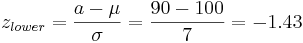
Busque valores de puntaje z en una tabla normal estándar. Medios:Grupo_G_Z-Tabla.xls

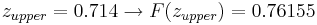
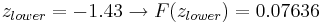
Entonces:

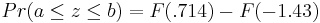
= 0.76155 - 0.07636

= 0.68479.

La probabilidad de medir una presión entre 90 y 105 psig es de 0.68479.

A continuación se muestra una representación gráfica de esto. El área sombreada es la probabilidad

Solución alternativa

También podemos resolver este problema usando la función de distribución de probabilidad (PDF). Esto se puede hacer fácilmente en Mathematica como se muestra a continuación. Puede encontrar más información sobre el PDF y cómo se usa en el artículo de Distribución Continua

Como puede ver el resultado es aproximadamente el mismo valor encontrado usando las puntuaciones z.

Ejemplo\(\PageIndex{2}\)

Eres ingeniero de calidad para la compañía farmacéutica “Headache-b-gone”. Usted está a cargo de la producción masiva del medicamento para el dolor de cabeza de sus hijos. Se supone que el peso promedio del acetaminofén en este medicamento es de 80 mg, sin embargo cuando realizas las pruebas requeridas encuentras que el peso promedio de 50 muestras aleatorias es de 79.95 mg con una desviación estándar de .18.

1. Identificar la hipótesis nula y alternativa.
2. ¿En qué condiciones se acepta la hipótesis nula?
3. Determinar si estas diferencias en el peso promedio son significativas.

Solución

a)

• Hipótesis nula: Este es el peso promedio reclamado donde H _o =80 mg
• Hipótesis alternativa: Esto es cualquier cosa que no sea el peso promedio reclamado (en este caso H _a <80)

b) Se acepta la hipótesis nula cuando el valor p es mayor que .05.

c) Primero necesitamos encontrar Z _obs usando la siguiente ecuación:

\[z_{o b s}=\frac{X-\mu}{\frac{\sigma}{\sqrt{n}}}\nonumber \]

Donde n es el número de muestras tomadas.

\[z_{o b s}=\frac{79.95-80}{\frac{.18}{\sqrt{50}}}=-1.96\nonumber \]

Usando la tabla de puntuación z proporcionada en secciones anteriores obtenemos un valor p de .025. Dado que este valor es menor que el valor de significancia (.05) rechazamos la hipótesis nula y determinamos que el producto no alcanza nuestros estándares.

Ejemplo\(\PageIndex{3}\)

Se encuestó a 15 estudiantes en una clase de controles para ver si la tarea afecta las calificaciones del examen. Se observa la siguiente distribución.

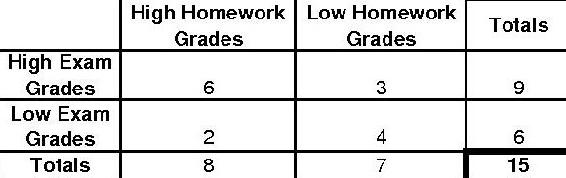
Determinar el valor p y si la hipótesis nula (La tarea no afecta a los exámenes) es significativa por un nivel de significancia de 5% utilizando el método p-Fisher.

Solución

Para encontrar el valor p usando el método p-fisher, primero debemos encontrar el p-fisher para la distribución original. Entonces, debemos encontrar al pescador p para cada caso más extremo. El pescador p para la distribución original es el siguiente.

\[p_{\text {fisher }}=\frac{9 ! 6 ! 8 ! 7 !}{15 ! 6 ! 3 ! 2 ! 4 !}=0.195804 \nonumber \]

Para encontrar el caso más extremo, gradualmente disminuiremos el número más pequeño a cero. Así, nuestra próxima distribución se vería como la siguiente.

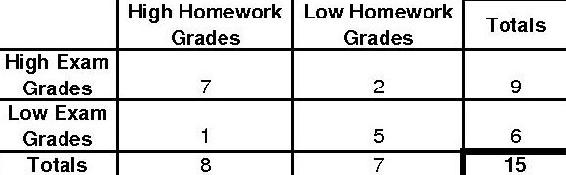
El pescador p para esta distribución será el siguiente.

\[p_{\text {fisher }}=\frac{9 ! 6 ! 8 ! 7 !}{15 ! 7 ! 2 ! 1 ! 5 !}=0.0335664 \nonumber \]

El último caso extremo se verá así.

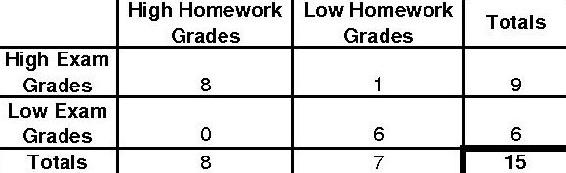
El pescador p para esta distribución será el siguiente.

\[p_{\text {fisher }}=\frac{9 ! 6 ! 8 ! 7 !}{15 ! 8 ! 1 ! 0 ! 6 !}=0.0013986\nonumber \]

Ya que tenemos un 0 ahora en la distribución, no hay casos más extremos posibles. Para encontrar el valor p sumaremos los valores de p-fisher de las 3 distribuciones diferentes.

\[p_{value} = 0.195804 + 0.0335664 + 0.0013986 = 0.230769\nonumber \]

Debido a que p-valor=0.230769 no podemos rechazar la hipótesis nula en un nivel de significancia del 5%.

Aplicación: ¿Qué nos dicen los valores p?

Ejemplo de Población

De una muestra aleatoria de 400 estudiantes que vivían en el dormitorio (grupo A), 134 estudiantes se resfriaron durante el ciclo escolar académico. De una muestra aleatoria de 1000 estudiantes que vivían fuera del campus (grupo B), 178 estudiantes se resfriaron durante este mismo periodo de tiempo.

Tabla de población

\ [\ begin {array} {llll}
&\ text {Graup A} &\ text {Grupo B} &\\
\ text {Enfermo} & a=134 & b=178 & a+b=312\
\ text {No Enfermo} & c=266 & d=822 & c+d=1088\\
& a+c=400 & b+d=1000 & a+b+c+d=1400
\ end {array}\ nonumber\]

Exacto de Fisher:

\[p_{f}=\frac{(a+b) !(c+d) !(a+c) !(b+d) !}{(a+b+c+d) ! a ! b ! c ! d !}\nonumber \]

Resolver:

\[p_{f}=\frac{(312) !(1088) !(400) !(1000) !}{(1400) ! 134 ! 178 ! 266 ! 822 !}\nonumber \]

p _f = 2.28292 * 10 ^{− 10}

Comparación e interpretación del valor p al nivel de confianza del 95%

Este valor es muy cercano a cero que es mucho menor que 0.05. Por lo tanto, el número de estudiantes que se enferman en el dormitorio es significativamente mayor que el número de estudiantes que se enferman fuera del campus. Hay más de un 95% de probabilidad de que esta diferencia significativa no sea aleatoria. Estadísticamente, se demuestra que este dormitorio es más conductivo para la propagación de virus. Con los conocimientos adquiridos a partir de este análisis, puede justificarse realizar cambios en el dormitorio. Quizás la instalación de dispensadores sanitarios en lugares comunes a lo largo del dormitorio disminuiría esta mayor prevalencia de enfermedad entre los estudiantes del dormitorio. La investigación adicional puede determinar áreas más específicas de propagación viral marcando varias poblaciones más pequeñas de estudiantes que viven en diferentes áreas del dormitorio. Este modelo de prueba de significancia es muy útil y a menudo se aplica a una multitud de datos para determinar si las discrepancias se deben a diferencias de azar o reales entre muestras de datos comparadas. Como puede ver, los análisis puramente matemáticos como estos suelen llevar a que se tomen acciones físicas, lo cual es necesario en el campo de la Medicina, la Ingeniería, y otros recintos científicos y no científicos.

Ejercicio\(\PageIndex{1}\)

Se le da el siguiente conjunto de datos: {1,2,3,5,5,6,7,7,7,9,12} ¿Cuál es la media, mediana y modo de este conjunto de datos? Y luego el valor z de un punto de datos de 7?

1. 5.82, 6, 7, 0.373
2. 6, 7, 5.82, 6.82
3. 7, 6, 5, 0.373
4. 7, 6, 5.82, 3.16

Contestar

a

Ejercicio\(\PageIndex{2}\)

¿Cuál es n y la desviación estándar para el conjunto de datos anterior {1,2,3,5,5,6,7,7,7,9,12}? Y luego consultando la tabla desde arriba, ¿cuál es el valor p para los datos “12"?

1. 12, 3.16, 5.82
2. 7, 3.16, 0.83
3. 11, 3.16, 0.97
4. 11, 5.82, 0

Contestar

c

Referencias

• Woolf P., Keating A., Burge C., y Michael Y.. “Imprimación Estadística y Probabilidad para Biólogos Computacionales”. Instituto Tecnológico de Massachusetts, BE 490/ Bio7.91, primavera de 2004
• Smith W. y Gonic L. “Cartoon Guide to Statistics”. Harper Perennial, 1993.
• Taylor, J. “Una introducción al análisis de errores”. Sausalito, CA: Libros de Ciencias Universitarias, 1982.
• http://www.fourmilab.ch/rpkp/experiments/analysis/zCalc.html