13.5: Teoría de Redes Bayesianas

Última actualización
Guardar como PDF

Page ID: 85495

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Introducción

La teoría de redes bayesianas se puede considerar como una fusión de diagramas de incidencia y teorema de Bayesian. Una red bayesiana, o red de creencias, muestra relaciones condicionales de probabilidad y causalidad entre variables. La probabilidad de que ocurra un evento dado que ya ocurrió otro evento se denomina probabilidad condicional. El modelo probabilístico es descrito cualitativamente por una gráfica acíclica dirigida, o DAG. Los vértices de la gráfica, que representan variables, se denominan nodos. Los nodos se representan como círculos que contienen el nombre de la variable. Las conexiones entre los nodos se denominan arcos o aristas. Los bordes se dibujan como flechas entre los nodos, y representan la dependencia entre las variables. Por lo tanto, para cualquier par de nodos indicar que un nodo es el padre del otro por lo que no hay supuestos de independencia. Los supuestos de independencia están implícitos en las redes bayesianas por la ausencia de un vínculo. Aquí hay un DAG de muestra:

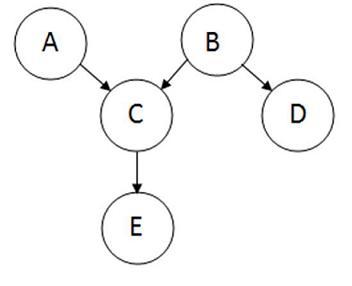
amplio BN.JPG

El nodo donde se origina el arco se llama padre, mientras que el nodo donde termina el arco se llama hijo. En este caso, A es padre de C, y C es hijo de A. Los nodos a los que se puede llegar desde otros nodos se llaman descendientes. Los nodos que conducen una ruta a un nodo específico se llaman ancestros. Por ejemplo, C y E son descendientes de A, y A y C son ancestros de E. No hay bucles en las redes bayesianas, ya que ningún niño puede ser su propio antepasado o descendiente. Las redes bayesianas generalmente también incluirán un conjunto de tablas de probabilidad, indicando las probabilidades para los valores verdadero/falso de las variables. El punto principal de las Redes Bayesianas es permitir que se realice una inferencia probabilística. Esto significa que la probabilidad de cada valor de un nodo en la red bayesiana se puede calcular cuando se conocen los valores de las otras variables. Además, debido a que la independencia entre las variables es fácil de reconocer ya que las relaciones condicionales están claramente definidas por el borde de una gráfica, no todas las probabilidades conjuntas en el sistema bayesiano necesitan ser calculadas para tomar una decisión.

Distribuciones de probabilidad conjunta

La probabilidad conjunta se define como la probabilidad de que una serie de eventos sucedan simultáneamente. La probabilidad conjunta de varias variables se puede calcular a partir del producto de probabilidades individuales de los nodos:

\[\mathrm{P}\left(X_{1}, \ldots, X_{n}\right)=\prod_{i=1}^{n} \mathrm{P}\left(X_{i} \mid \text { parents }\left(X_{i}\right)\right) \nonumber \]

Usando el gráfico de muestra de la introducción, la distribución conjunta de probabilidad es:

\[P(A, B, C, D, E)=P(A) P(B) P(C \mid A, B) P(D \mid B) P(E \mid C) \nonumber \]

Si un nodo no tiene un padre, como el nodo A, su distribución de probabilidad se describe como incondicional. De lo contrario, la distribución de probabilidad local del nodo está condicionada a otros nodos.

Clases de equivalencia

Cada red bayesiana pertenece a un grupo de redes bayesianas conocidas como clase de equivalencia. En una clase de equivalencia dada, todas las redes bayesianas pueden ser descritas por la misma declaración de probabilidad conjunta. Como ejemplo, el siguiente conjunto de redes bayesianas comprende una clase de equivalencia:

Red 1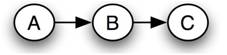 etwork 1.jpg

Red 2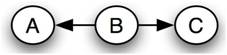 etwork 2.jpg

Red 3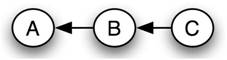 etwork 3.jpg

La causalidad que implica cada una de estas redes es diferente, pero la misma declaración de probabilidad conjunta las describe todas. Las siguientes ecuaciones demuestran cómo se puede crear cada red a partir de la misma declaración de probabilidad conjunta original:

Red 1

\[P(A, B, C)=P(A) P(B \mid A) P(C \mid B) \nonumber \]

Red 2

\[\begin{align*} P(A, B, C) &=P(A) P(B \mid A) P(C \mid B) \\[4pt] &=P(A) \frac{P(A \mid B) P(B)}{P(A)} P(C \mid B) \\[4pt] &=P(A \mid B) P(B) P(C \mid B) \end{align*} \nonumber \]

Red 3

A partir de ahora desde el comunicado de la Red 2

\[\begin{align*} P(A, B, C) &=P(A \mid B) P(B) P(C \mid B) \\[4pt] &=P(A \mid B) P(B) \frac{P(B \mid C) P(C)}{P(B)} \\[4pt] &=P(A \mid B) P(B \mid C) P(C)\end{align*} \nonumber \]

Todas las sustituciones se basan en la regla de Bayes.

La existencia de clases de equivalencia demuestra que la causalidad no puede determinarse a partir de observaciones aleatorias. Un estudio controlado —que mantiene constantes algunas variables mientras varía otras para determinar el efecto de cada una— es necesario para determinar la relación causal exacta, o red bayesiana, de un conjunto de variables.

Teorema de Bayes

El teorema de Bayes, desarrollado por el reverendo Thomas Bayes, matemático y teólogo del siglo XVIII, se expresa como:

\[P(H \mid E, c)=\frac{P(H \mid c) \cdot P(E \mid H, c)}{P(E \mid c)} \nonumber \]

donde podemos actualizar nuestra creencia en la hipótesis$H$ dada la evidencia adicional$E$ y la información de fondo$c$. El término de la izquierda,$P(H|E,c)$ se conoce como la “probabilidad posterior”, o la probabilidad de H después de considerar el efecto de E dado c. El término$P(H|c)$ se llama la “probabilidad previa” de c$H$ dada sola. El término$P(E|H,c)$ se denomina “verosimilitud” y da la probabilidad de que la evidencia asuma la hipótesis$H$ y la información de fondo$c$ es verdadera. Por último, al último término$P(E|c)$ se le llama la “expectativa”, o cómo se espera se da únicamente la evidencia$c$. Es independiente$H$ y puede considerarse como un factor de marginación o escalamiento.

Se puede reescribir como

\[P(E \mid c)=\sum_{i} P\left(E \mid H_{i}, c\right) \cdot P\left(H_{i} \mid c\right) \nonumber \]

donde i denota una hipótesis específica H _i, y la suma se toma sobre un conjunto de hipótesis que son mutuamente excluyentes y exhaustivas (sus probabilidades previas suman a 1).

Es importante señalar que todas estas probabilidades son condicionales. Precisan el grado de creencia en alguna proposición o proposiciones con base en el supuesto de que algunas otras proposiciones son verdaderas. Como tal, la teoría no tiene sentido sin la determinación previa de la probabilidad de estas proposiciones anteriores.

Factor de Bayes

En los casos en que no esté seguro de las relaciones causales entre las variables y el resultado al construir un modelo, puede usar el Factor Bayes para verificar qué modelo describe mejor sus datos y, por lo tanto, determinar en qué medida un parámetro afecta el resultado de la probabilidad. Después de usar el Teorema de Bayes para construir dos modelos con diferentes relaciones de dependencia de variables y evaluar la probabilidad de los modelos a partir de los datos, se puede calcular el Factor de Bayes usando la siguiente ecuación general:

\[B F=\frac{p(\text {model} 1 \mid \text {data})}{p(\text {model} 2 \mid \text {data})}=\frac{\frac{p(\text {data} \mid \text {model} 1) p(\text {model} 1)}{p(\text {data})}}{\frac{p(\text {data} \mid \operatorname{model} 2) p(\operatorname{model} 2)}{p(\text {data})}}=\frac{p(\text {data} \mid \text {model} 1)}{p(\text {data} \mid \operatorname{model} 2)} \nonumber \]

La intuición básica es que la información previa y posterior se combinan en una proporción que proporciona evidencia a favor de un modelo frente al otro. Los dos modelos de la ecuación del Factor de Bayes representan dos estados diferentes de las variables que influyen en los datos. Por ejemplo, si los datos que se están estudiando son mediciones de temperatura tomadas de múltiples sensores, el Modelo 1 podría ser la probabilidad de que todos los sensores estén funcionando normalmente, y el Modelo 2 la probabilidad de que todos los sensores hayan fallado. Los factores de Bayes son muy flexibles, lo que permite comparar múltiples hipótesis simultáneamente.

Los valores de BF cercanos a 1, indican que los dos modelos son casi idénticos y los valores de BF lejos de 1 indican que la probabilidad de que ocurra un modelo es mayor que el otro. Específicamente, si BF es > 1, el modelo 1 describe sus datos mejor que el modelo 2. Si BF es < 1, el modelo 2 describe los datos mejor que el modelo 1. En nuestro ejemplo, si un factor de Bayes' de 5 indicara que dados los datos de temperatura, la probabilidad de que los sensores funcionen normalmente es cinco veces mayor que la probabilidad de que los senores fallaran. A continuación se puede encontrar una tabla que muestra la escala de evidencias utilizando el Factor Bayes:

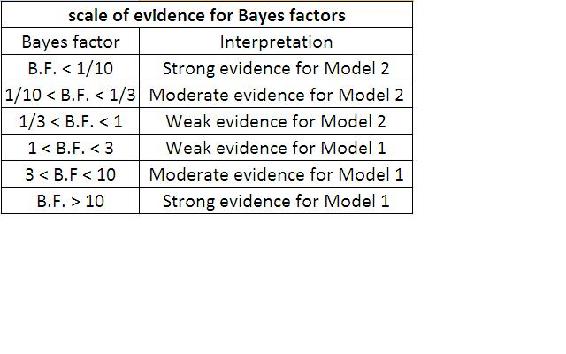
ayes Factor.jpg

Aunque los Factores de Bayes son bastante intuitivos y fáciles de entender, como cuestión práctica suelen ser bastante difíciles de calcular. Existen alternativas al Factor Bayes para la evaluación de modelos como el Criterio Bayesiano de Información (BIC).

La fórmula para el BIC es:

\[-2 \cdot \ln p(x \mid k) \approx \mathrm{BIC}=-2 \cdot \ln L+k \ln (n). \nonumber \]

x = los datos observados; n = el número de puntos de datos en x, el número de observaciones, o equivalentemente, el tamaño de la muestra;
k = el número de parámetros libres a estimar. Si el modelo estimado es una regresión lineal, k es el número de regresores, incluyendo la constante; p (x|k) = la probabilidad de los datos observados dado el número de parámetros;
L = el valor maximizado de la función de verosimilitud para el modelo estimado.

Esta estadística también se puede utilizar para modelos no anidados. Para mayor información sobre el Criterio de Información Bayesiana, por favor refiérase a:

Ventajas y limitaciones de las redes bayesianas

Las ventajas de las Redes Bayesianas son las siguientes:

Las Redes Bayesianas representan visualmente todas las relaciones entre las variables en el sistema con arcos de conexión.
Es fácil reconocer la dependencia e independencia entre varios nodos.
Las redes bayesianas pueden manejar situaciones en las que el conjunto de datos está incompleto ya que el modelo da cuenta de las dependencias entre todas las variables.
Las redes bayesianas pueden mapear escenarios donde no es factible/práctico medir todas las variables debido a las limitaciones del sistema (costos, falta de suficientes sensores, etc.)
Ayuda a modelar sistemas ruidosos.
Se puede utilizar para cualquier modelo de sistema, desde todos los parámetros conocidos hasta ningún parámetro conocido.

Las limitaciones de las Redes Bayesianas son las siguientes:

Todas las sucursales deben ser calculadas para calcular la probabilidad de cualquier rama.
La calidad de los resultados de la red depende de la calidad de las creencias o modelos previos. Una variable es solo una parte de una red bayesiana si crees que el sistema depende de ella.
El cálculo de la red es NP-duro (polinomio-tiempo no determinista duro), por lo que es muy difícil y posiblemente costoso.
Los cálculos y probabilidades utilizando la regla y marginación de Baye pueden volverse complejos y a menudo se caracterizan por una redacción sutil, y se debe tener cuidado para calcularlos adecuadamente.

Inferencia

La inferencia se define como el proceso de derivar conclusiones lógicas basadas en premisas conocidas o asumidas como verdaderas. Una fortaleza de las redes bayesianas es la capacidad de inferencia, que en este caso involucra las probabilidades de variables no observadas en el sistema. Cuando se sabe que las variables observadas están en un estado, las probabilidades de otras variables tendrán valores diferentes a los del caso genérico. Tomemos un sistema de ejemplo sencillo, una televisión. La probabilidad de que una televisión esté encendida mientras la gente está en casa es mucho mayor que la probabilidad de que esa televisión esté encendida cuando no hay nadie en casa. Si se conoce el estado actual de la televisión, la probabilidad de que las personas estén en casa se puede calcular con base en esta información. Esto es difícil de hacer a mano, pero los programas de software que utilizan redes bayesianas incorporan inferencia. Uno de esos programas de software, Genie, se introduce en Aprender y analizar las redes bayesianas con Genie.

Marginación

La marginación de un parámetro en un sistema puede ser necesaria en algunos casos:

Si los datos para un parámetro (P1) dependen de otro, y no se proporcionan datos para el parámetro independiente.
Si se da una tabla de probabilidad en la que P1 depende de otros dos parámetros del sistema, pero solo le interesa el efecto de uno de los parámetros en P1.

Imagine un sistema en el que un cierto reactivo (R) se mezcla en un CSTR con un catalizador (C) y da como resultado un cierto rendimiento de producto (Y). Se están probando tres concentraciones de reactivos (A, B y C) con dos catalizadores diferentes (1 y 2) para determinar qué combinación dará el mejor rendimiento del producto. La declaración de probabilidad condicional se ve como tal:

\[P(R, C, Y)=P(R) P(C) P(Y \mid R, C) \nonumber \]

La tabla de probabilidad se establece de tal manera que la probabilidad de cierto rendimiento de producto depende de la concentración de reactivo y del tipo de catalizador. Desea predecir la probabilidad de cierto rendimiento de producto dado solo los datos que tiene para el tipo de catalizador. La concentración de reactivo debe ser marginada de P (Y|R, C) para determinar la probabilidad del rendimiento del producto sin conocer la concentración del reactivo. Por lo tanto, es necesario determinar P (Y|C). La ecuación de marginación se muestra a continuación:

\[P(Y \mid C)=\sum_{i} P\left(Y \mid R_{i}, C\right) P\left(R_{i}\right) \nonumber \]

donde se toma la suma sobre las concentraciones de reactantes A, B y C.

La siguiente tabla describe la probabilidad de que una muestra se pruebe con la concentración de reactante A, B o C:

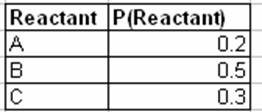
En la siguiente tabla se describe la probabilidad de observar un rendimiento - Alto (H), Medio (M) o Bajo (L) - dada la concentración de reactivo y el tipo de catalizador:

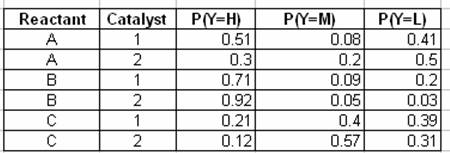
Las dos tablas finales muestran el cálculo de las probabilidades marginadas de rendimiento dado un tipo de catalizador usando la ecuación de marginación:

Redes Bayesianas Dinámicas

La red bayesiana estática solo funciona con resultados variables de un solo intervalo de tiempo. Como resultado, una red bayesiana estática no funciona para analizar un sistema en evolución que cambia con el tiempo. A continuación se muestra un ejemplo de una red bayesiana estática para un catter petrolero:

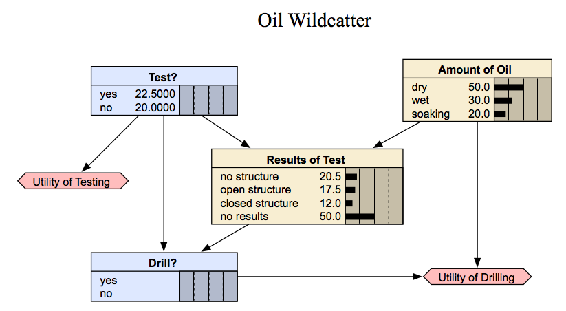
www.norsys.com/netlibrary/index.htm

Un catter petrolero debe decidir perforar o no. Sin embargo, necesita determinar si el agujero está seco, húmedo o remojo. El catter salvaje podría tomar sondeos sísmicos, que ayudan a determinar la estructura geológica en el sitio. Los sondeos revelarán si el terreno de abajo no tiene estructura, lo cual es malo, o estructura abierta que está bien, o estructura cerrada, lo cual es realmente bueno. Como puedes ver este ejemplo no depende del tiempo.

La Red Bayesiana Dinámica (DBN) es una extensión de la Red Bayesiana. Se utiliza para describir cómo las variables se influyen entre sí a lo largo del tiempo con base en el modelo derivado de datos pasados. Un DBN puede pensarse como un modelo de cadena de Markov con muchos estados o una aproximación de tiempo discreta de una ecuación diferencial con pasos de tiempo.

Un ejemplo de un DBN, que se muestra a continuación, es una bola sin fricción que rebota entre dos barreras. En cada paso de tiempo cambia la posición y la velocidad.

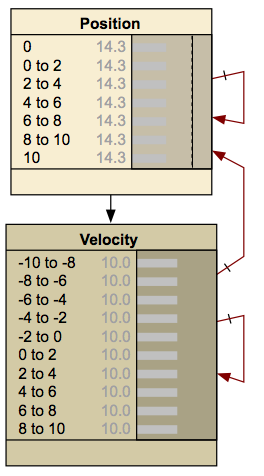
www.norsys.com/netlibrary/index.htm

Se debe hacer una distinción importante entre los DBN y las cadenas de Markov. Un DBN muestra cómo las variables se afectan entre sí a lo largo del tiempo, mientras que una cadena de Markov muestra cómo evoluciona el estado de todo el sistema a lo largo del tiempo. Así, un DBN ilustrará las probabilidades de que una variable cambie a otra, y cómo cada una de las variables individuales cambiará con el tiempo. Una cadena de Markov analiza el estado de un sistema, que incorpora el estado de cada variable individual que compone el sistema, y muestra las probabilidades de que el sistema cambie de estado a lo largo del tiempo. Por lo tanto, una cadena de Markov incorpora todas las variables presentes en el sistema al observar cómo evoluciona dicho sistema a lo largo del tiempo. Las cadenas de Markov se pueden derivar de los DBN, pero cada red representa diferentes valores y probabilidades.

La creación de un DBN tiene varias ventajas. Una vez que se ha establecido la red entre los pasos de tiempo, se puede desarrollar un modelo basado en estos datos. Este modelo puede entonces ser utilizado para predecir respuestas futuras por parte del sistema. La capacidad de predecir respuestas futuras también se puede utilizar para explorar diferentes alternativas para el sistema y determinar qué alternativa da los resultados deseados. Los DBN también proporcionan un entorno adecuado para controladores predictivos de modelos y pueden ser útiles para crear el controlador. Otra ventaja de los DBN es que pueden ser utilizados para crear una red general que no dependa del tiempo. Una vez que se ha establecido el DBN para los diferentes pasos de tiempo, la red puede colapsarse para eliminar el componente de tiempo y mostrar las relaciones generales entre las variables.

Un DBN se compone de intervalos de tiempo interconectados de redes bayesianas estáticas. Los nodos en cierto tiempo pueden afectar a los nodos en un segmento de tiempo futuro, pero los nodos en el futuro no pueden afectar a los nodos en el segmento de tiempo anterior. Los vínculos causales a través de los intervalos de tiempo se conocen como enlaces temporales, el beneficio de esto es que le da a DBN una dirección inequívoca de causalidad.

Para la comodidad del cálculo, se supone que las variables en DBN tienen un número finito de estados que puede tener la variable. En base a esto, se pueden construir tablas de probabilidad condicional para expresar las probabilidades de cada nodo hijo derivadas de las condiciones de sus nodos padres.

El nodo C del DAG de muestra anterior tendría una tabla de probabilidad condicional especificando la distribución condicional P (C|A, B). Ya que A y B no tienen padres, por lo que solo requieren distribuciones de probabilidad P (A) y P (B). Suponiendo que todas las variables son binarias, la variable media A solo puede tomar A1 y A2, la variable B solo puede tomar B1 y B2, y la variable C solo puede tomar C1 y C2. A continuación se muestra un ejemplo de una tabla de probabilidad condicional del nodo C.

Las probabilidades condicionales entre nodos de observación se definen usando un nodo sensor. Este nodo sensor proporciona una distribución de probabilidad condicional de la lectura del sensor dado el estado real del sistema. Encarna la precisión del sistema.

La naturaleza de DBN generalmente resulta en una red grande y compleja. Por lo tanto, para calcular un DBN, el segmento de tiempo antiguo de resultado se resume en probabilidades que se usan para el segmento posterior. Esto proporciona un marco de tiempo móvil y forma un DBN. Al crear un DBN, se deben tener en cuenta las relaciones temporales entre los sectores. A continuación se muestra una tabla de implementación para DBN.

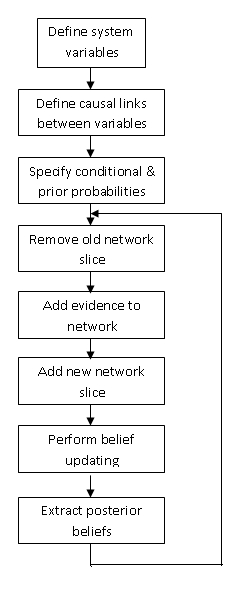
La gráfica a continuación es una representación de un DBN. Representa las variables en dos etapas de tiempo diferentes, t-1 y t. t-1, que se muestra a la izquierda, es la distribución inicial de las variables. El siguiente paso de tiempo, t, depende del paso de tiempo t-1. Es importante señalar que algunas de estas variables podrían estar ocultas.

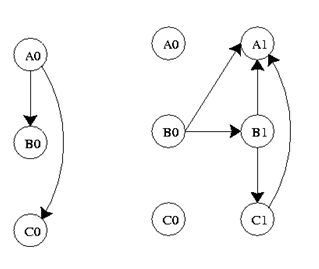
Donde Ao, Bo, Co son estados iniciales y Ai, Bi, Ci son estados futuros donde i=1,2,3,..., n.

La distribución de probabilidad para este DBN en el tiempo t es...

\[P\left(Z_{t} \mid Z_{t-1}\right)=\prod_{i=1}^{N} P\left(Z_{t}^{i} \mid \pi\left(Z_{t}^{i}\right)\right) \nonumber \]

Si el proceso continúa durante un mayor número de pasos de tiempo, la gráfica tomará la forma a continuación.

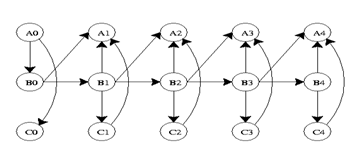
Su distribución conjunta de probabilidad será...

\[P\left(Z_{1: T}\right)=\prod_{t=1}^{T} \prod_{i=1}^{N} P\left(Z_{t}^{i} \mid \pi\left(Z_{t}^{i}\right)\right) \nonumber \]

Los DBN son útiles en la industria porque pueden modelar procesos donde la información está incompleta, o hay incertidumbre. Las limitaciones de los DBN son que no siempre predicen con precisión los resultados y pueden tener largos tiempos computacionales.

Las ilustraciones anteriores son todas ejemplos de redes “desenrolladas”. Una red bayesiana dinámica desenrollada muestra cómo cada variable en un paso de tiempo afecta a las variables en el siguiente paso de tiempo. Una manera útil de pensar en redes desenrolladas es como representaciones visuales de soluciones numéricas a ecuaciones diferenciales. Si conoces los estados de las variables en un momento dado, y sabes cómo cambian las variables con el tiempo, entonces puedes predecir cuál será el estado de las variables en cualquier momento, similar a usar el método de Euler para resolver una ecuación diferencial. Una red bayesiana dinámica también se puede representar como una red “enrollada”. Una red laminada, a diferencia de una red desenrollada, muestra el efecto de cada variable en una gráfica. Por ejemplo, si tuvieras una red desenrollada del formulario:

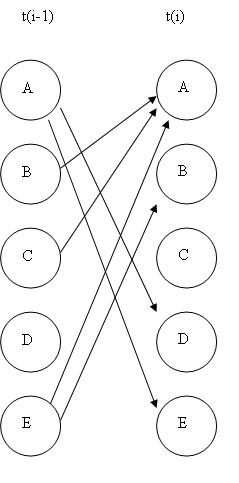
BN (desenrollado) .jpg

entonces podrías representar esa misma red en forma enrollada como:

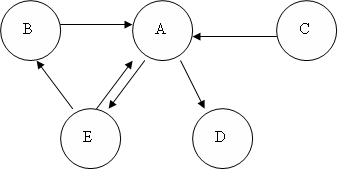
BN (enrollado) .jpg

Si examina cada red, verá que cada una proporciona exactamente la misma información en cuanto a cómo todas las variables se afectan entre sí.

Aplicaciones

Las redes bayesianas se utilizan cuando la probabilidad de que ocurra un evento depende de la probabilidad de que ocurra un evento anterior. Esto es muy importante en la industria porque en muchos procesos, las variables tienen relaciones condicionales, es decir, no son independientes entre sí. Las redes bayesianas se utilizan para modelar procesos en una amplia variedad de aplicaciones. Algunos de estos incluyen...

Redes reguladoras génicas
Estructura proteica
Diagnóstico de enfermedad
Clasificación de documentos
Procesamiento de imágenes
Fusión de datos
Sistemas de apoyo a la decisión
Recopilación de datos para la exploración del espacio profundo
Inteligencia Artificial
Predicción del tiempo
De manera más familiar, las redes bayesianas son utilizadas por el amigable asistente de oficina de Microsoft para obtener mejores resultados de búsqueda. \
Otro uso de las redes bayesianas surge en la industria crediticia donde a un individuo se le puede asignar un puntaje crediticio basado en la edad, salario, historial crediticio, etc. Esto se alimenta a una red bayesiana que permite a las compañías de tarjetas de crédito decidir si el puntaje crediticio de la persona merece una aplicación favorable.

Resumen: Un algoritmo de solución general para los perplejos

Ante un problema de red bayesiana y sin idea de por dónde empezar, simplemente relájate e intenta seguir los pasos que se describen a continuación.

Paso 1: ¿Qué aspecto tiene mi red? ¿Qué nodos son los padres (y son condicionales o incondicionales) y cuáles son los hijos? ¿Cómo modelaría esto como un diagrama de incidencia y qué declaración de probabilidad condicional lo define?

Paso 2: Dada mi conectividad de red, ¿cómo tabulo las probabilidades para cada estado de mi (s) nodo (s) de interés? Para una sola columna de probabilidades (nodo padre), ¿la columna suma a 1? Para una matriz de probabilidades (nodo hijo) con múltiples estados posibles definidos por la combinación dada de estados de nodo padre, ¿las filas suman a 1?

Paso 3: Dado un conjunto de datos observados (generalmente estados de un nodo hijo de interés), y tablas de probabilidad (también conocidas como tablas de verdad), ¿qué problema estoy resolviendo?

Probabilidad de observar la configuración particular de los datos, orden sin importancia

Solución: Aplicar distribución multinomial

Probabilidad de observar la configuración particular de los datos en ese orden particular

Solución: Calcule la probabilidad de cada observación individual, luego tome el producto de estas

Probabilidad de observar los datos en un nodo hijo definido por 2 (o n) padres dados solo 1 (o n-1) de los nodos padre

Solución: Aplicar marginación para eliminar otro nodo padre

Probabilidad de que un nodo padre sea un estado particular dado datos en forma de estados observados del nodo hijo

Solución: Aplicar el Teorema de Bayes'
Resolver para el Factor de Bayes para eliminar términos de denominador incalculables generados al aplicar el Teorema de Bayes, y para comparar el estado de interés del nodo padre con un caso base, produciendo un punto de datos más significativo

Paso 4: ¿He resuelto el problema? ¿O hay otro nivel de complejidad? ¿El problema es una combinación de las variaciones del problema enumeradas en el paso 3?

Si el problema se soluciona, llámalo un día y ve a tomar un descanso de baklava
Si el problema no se resuelve, regrese al paso 3

Gráficamente:

Ejemplo$\PageIndex{1}$

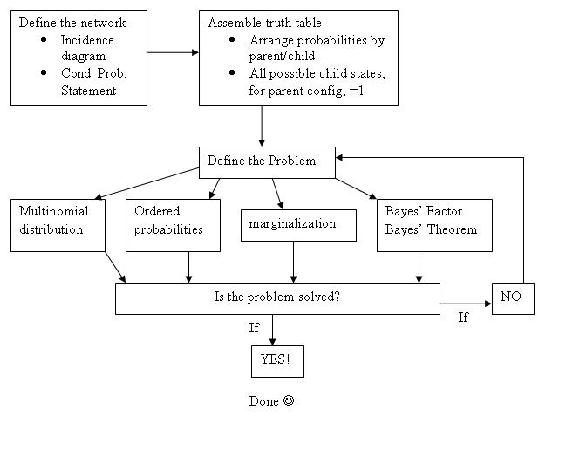
Una alarma multipropósito en una planta se puede activar de 2 maneras. La alarma se apaga si la temperatura del reactor es demasiado alta o la presión en un tanque de almacenamiento es demasiado alta. La temperatura del reactor puede ser demasiado alta debido a un flujo de agua de enfriamiento bajo (1% de probabilidad), o por una reacción secundaria desconocida (5% de probabilidad). La presión del tanque de almacenamiento podría ser demasiado alta debido a un bloqueo en la tubería de salida (2% de probabilidad). Si el flujo de agua de enfriamiento es bajo y hay una reacción secundaria, entonces hay una probabilidad del 99% de que ocurra una temperatura alta. Si el flujo de agua de enfriamiento es normal y no hay reacción secundaria, solo hay un 3% de probabilidad de que ocurra una temperatura alta. Si hay un bloqueo de tubería, siempre se producirá una alta presión. Si no hay obstrucción de tuberías, se producirá una alta presión solo el 2% del tiempo.

Crear un DAG para la situación anterior y configurar las tablas de probabilidad necesarias para modelar este sistema. No se dan todos los valores requeridos para rellenar estas tablas, así que rellene lo que sea posible y luego indique qué valores adicionales se necesitan encontrar.

Solución

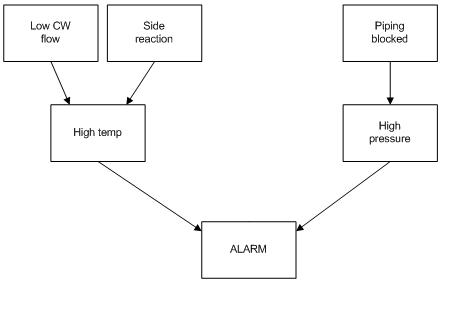
En las siguientes tablas de probabilidad se describe el sistema, donde CFL = El flujo de agua fría es bajo, SR = Reacción lateral presente, PB = Tubería bloqueada, HT = Alta temperatura, HP = Alta presión, A = Alarma. T significa verdadero, o el evento sí ocurrió. F significa falso, o el evento no ocurrió. Un espacio en blanco en una tabla indica un área donde se necesita más información.

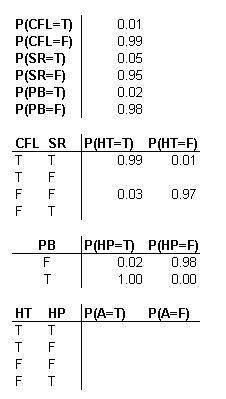
xample1 2.JPG

Una ventaja de usar DAG se hace evidente. Por ejemplo, puedes ver que solo hay un 3% de probabilidad de que haya una situación de alta temperatura dado que tanto el flujo de agua fría no es bajo y que no hay reacción lateral.Sin embargo, tan pronto como el agua fría se vuelve baja, tienes al menos un 94% de probabilidad de una alarma de alta temperatura, independientemente de si o no se produce una reacción secundaria. Por el contrario, la presencia de una reacción secundaria aquí solo crea un 90% de probabilidad de activación de alarma. A partir de los cálculos de probabilidad anteriores, se puede estimar el dominio relativo de los desencadenantes de causa y efecto. Por ejemplo, ahora podría conjeturar razonablemente que el agua fría al ser baja es un evento más grave que una reacción secundaria.

Ejemplo$\PageIndex{2}$

El DAG que se da a continuación representa un modelo diferente en el que la alarma sonará cuando se active por fugas de alta temperatura y/o tubería de agua refrigerante en el reactor.

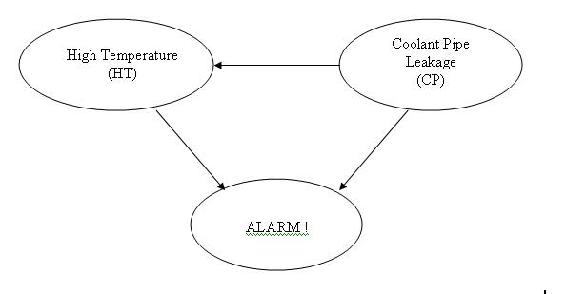
La siguiente tabla muestra la tabla de verdad y las probabilidades con respecto a las diferentes situaciones que podrían ocurrir en este modelo.

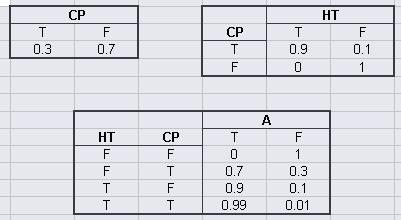
La función de probabilidad conjunta es:

\[P(A,HT,CP) = P(A | HT,CP)P(HT | CP)P(CP) \nonumber \]

Una gran característica del uso de la red bayesiana es que se puede calcular la probabilidad de cualquier situación. En este ejemplo, escriba el enunciado que describirá la probabilidad de que la temperatura sea alta en el reactor dado que sonó la alarma.

Solución

\[\mathrm{P}(C P=T \mid \Delta=T)=\frac{\mathrm{P}(A=T, C P=T)}{\mathrm{P}(A=1)} [= \dfrac{\sum_{HTC[T,P]}P(A-T, HT, CP-T)}{\sum_{HT, CPC[T,P]}P(A=T, HT, CP)} \nonumber \]

Ejemplo$\PageIndex{3}$

Ciertos medicamentos y traumas pueden causar coágulos de sangre. Un coágulo de sangre puede provocar un derrame cerebral, un ataque cardíaco o simplemente podría disolverse por sí solo y no tener implicaciones para la salud. Crear un DAG que represente esta situación.

Solución

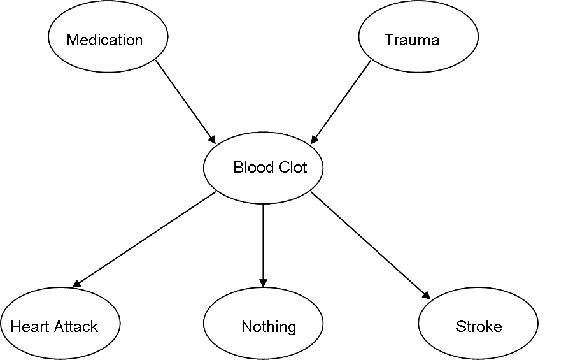
AG Ex3.png

b. Se da la siguiente información de probabilidad donde M = medicación, T = trauma, BC = coágulo de sangre, HA = ataque cardíaco, N = nada y S = accidente cerebrovascular. T significa verdadero, o este evento sí ocurrió. F significa falso, o este evento no ocurrió.

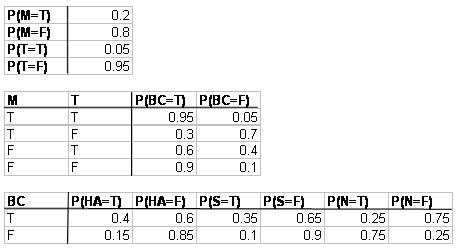
¿Cuál es la probabilidad de que una persona desarrolle un coágulo de sangre como resultado tanto de la medicación como del trauma, y entonces no tenga implicaciones médicas?

Responder

\[\mathrm{P}(\mathrm{N}, \mathrm{BC}, \mathrm{M}, \mathrm{T})=\mathrm{P}(\mathrm{N} \mid \mathrm{BC}) \mathrm{P}(\mathrm{BC} \mid \mathrm{M}, \mathrm{T}) \mathrm{P}(\mathrm{M}) \mathrm{P}(\mathrm{T})=(0.25)(0.95)(0.2)(0.05)=0.2375 \% \nonumber \]

Ejemplo$\PageIndex{4}$

Supongamos que te dieron los siguientes datos.

Catalizador	p (Catalizador)
A	0.40
B	0.60

Temperatura	Catalizador	P (Rendimiento = H)	P (Rendimiento = M)	P (Rendimiento = L)
H	A	0.51	0.08	0.41
H	B	0.30	0.20	0.50
M	A	0.71	0.09	0.20
M	B	0.92	0.05	0.03
L	A	0.21	0.40	0.39
L	B	0.12	0.57	0.31

¿Cómo usarías estos datos para encontrar p (rendield|temp) para 9 observaciones con las siguientes descripciones?

# Veces Observadas	Temperatura	Rendimiento
4x	H	H
2x	M	L
3x	L	H

Un DAG de este sistema se encuentra a continuación:

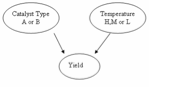
Imagen

Solución

¡Marginación! El estado del catalizador puede ser marginado usando la siguiente ecuación:

p (rendimiento \| temp) =	∑	p (rendimiento \| temp, cat _i) p (cat _i)
	i = A, B

Las dos tablas anteriores se pueden fusionar para formar una nueva tabla con marginación:

Temperatura	P (Rendimiento = H)	P (Rendimiento = M)	P (Rendimiento = L)
H	0.510.4 + 0.30.6 = 0.384	0.080.4 + 0.20.6 = 0.152	0.410.4 + 0.50.6 = 0.464
M	0.710.4 + 0.920.6 = 0.836	0.090.4 + 0.050.6 = 0.066	0.200.4 + 0.030.6 = 0.098
L	0.210.4 + 0.120.6 = 0.156	0.400.4 + 0.570.6 = 0.502	0.390.4 + 0.310.6 = 0.342

\[p(\text {yield} \mid \text {temp})=\frac{9 !}{4 ! 2 ! 3 !} *\left(0.384^{4} * 0.098^{2} * 0.156^{3}\right)=0.0009989 \nonumber \]

Ejemplo$\PageIndex{5}$

Un uso muy útil de las redes bayesianas es determinar si un sensor es más probable que funcione o se rompa en base a lecturas de corriente utilizando el Factor Bayesiano discutido anteriormente. Supongamos que hay una tina grande en tu proceso con gran flujo turbulento que dificulta medir con precisión el nivel dentro de la cuba. Para ayudarle a usar dos sensores de nivel diferentes ubicados alrededor del tanque que leen si el nivel es alto, normal o bajo. Cuando configuró por primera vez el sistema de sensores, obtuvo las siguientes probabilidades que describen el ruido de un sensor que funciona normalmente.

Nivel del Tanque (L)	p (S=Alto)	p (S=Normal)	p (S=Bajo)
Por encima del rango de nivel operativo	0.80	0.15	0.05
Dentro del rango de nivel operativo	0.15	0.75	0.10
Por debajo del rango de nivel operativo	0.10	0.20	0.70

Cuando el sensor falla, existe la misma posibilidad de que el sensor informe alto, normal o bajo independientemente del estado real del tanque. La tabla de probabilidad condicional para un sensor de falla se ve así:

Nivel del Tanque (L)	p (S=Alto)	p (S=Normal)	p (S=Bajo)
Por encima del rango de nivel operativo	0.33	0.33	0.33
Dentro del rango de nivel operativo	0.33	0.33	0.33
Por debajo del rango de nivel operativo	0.33	0.33	0.33

A partir de datos anteriores se ha determinado que cuando el proceso está actuando normalmente, como cree que es ahora, el tanque estará operando por encima del rango de nivel 10% del tiempo, dentro del rango de nivel 85% del tiempo, y por debajo del rango de nivel 5% del tiempo. Al observar las últimas 10 observaciones (que se muestran a continuación) sospecha que el sensor 1 puede estar roto. Utilice factores bayesianos para determinar la probabilidad de que el sensor 1 se rompa en comparación con ambos sensores funcionando.

Sensor 1	Sensor 2
Alto	Normal
Normal	Normal
Normal	Normal
Alto	Alto
Bajo	Normal
Bajo	Normal
Bajo	Bajo
Alto	Normal
Alto	Alto
Normal	Normal

De la definición del Factor Bayesiano obtenemos.

$F=\ frac {p (modelo 1|datos)} {p (modelo 2|datos)} =\ frac {\ frac {p (datos|modelo 1) p (modelo 1)} {p (datos)}} {\ frac {p (datos|modelo 2) p (modelo 2)} {p (datos)}} =\ frac {p (datos|modelo 1)} {p (datos|modelo 2)}$

Para este conjunto usaremos la probabilidad de que obtengamos los datos dados en base al modelo.

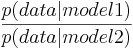
$frac {p (datos|modelo 1)} {p (datos|modelo 2)}$

Si consideramos que el modelo 1 funciona tanto los sensores como el modelo 2 sensor 2 que están rotos podemos encontrar el BF para esto con bastante facilidad.

p (datos | modelo 1) = p (s1 datos | modelo 1) *p (s2 datos | modelo 1)

Para ambos sensores que funcionan correctamente:

La probabilidad de que el sensor dé cada lectura tiene que calcularse primero, lo que se puede encontrar sumando la probabilidad de que el tanque esté en cada nivel y multiplicando por la probabilidad de obtener una lectura específica en ese nivel para cada nivel.

p (s1 = alto | modelo 1) = [(.10) * (.80) + (.85) * (.15) + (.05) * (.10) = 0.2125

p (s1 = normal | modelo 1) = [(.10) * (.15) + (.85) * (.75) + (.05) * (.20) = 0.6625

p (s1 = bajo | modelo 1) = [(.10) * (.05) + (.85) * (.10) + (.05) * (.70) = 0.125

Probabilidad de obtener las lecturas del sensor 1 (suponiendo que funcione normalmente)

p (s 1 datos | modelo 1) = (.2125) ⁴ * (.6625) ³ * (.125) ³ = 5.450 * 10 ^{− 6}

La probabilidad de obtener cada lectura para el sensor 2 será la misma ya que también está funcionando normalmente

p (s 2 datos | modelo 1) = (.2125) ² * (.6625) ⁷ * (.125) ¹ = 3.162 * 10 ^{− 4}

p (datos | modelo 1) = (5.450 * 10 ^{− 6}) * (3.162 * 10 ^{− 4}) = 1.723 * 10 ^{− 9}

Para el sensor 1 que está roto:

La probabilidad de obtener cada lectura ahora para el sensor uno será de 0.33.

p (s 1 datos | modelo 2) = (0.33) ⁴ * (0.33) ³ * (0.33) ³ = 1.532 * 10 ^{− 5}

La probabilidad de obtener las lecturas para el sensor 2 será la misma que la del modelo 1, ya que ambos modelos asumen que el sensor 2 está funcionando normalmente.

p (datos | modelo 2) = (1.532 * 10 ^{− 5}) * (3.162 * 10 ^{− 4}) = 4.844 * 10 ^{− 9}

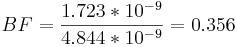
$BF =\ frac {1.723 * 10^ {-9}} {4.844 * 10^ {-9}} =0.356$

Un factor BF entre 1/3 y 1 significa que hay evidencia débil de que el modelo 2 es correcto.

¿Verdadero o Falso?

1. ¿El otro nombre para Bayesian Network es la Red “Creyente”?

2. Los nodos en una red bayesiana pueden representar cualquier tipo de variable (variable latente, parámetro medido, hipótesis..) y no están restringidos a variables aleatorias.

3. La teoría de redes bayesianas se utiliza en parte del proceso de modelado para la inteligencia artificial.

Respuestas:

1. F

2. T

3. T

Referencias

Aksoy, Selim. “Modelos Paramétricos Parte IV: Redes Bayesianas de Creencias”. Primavera 2007. <www.cs.bilkent.edu.tr/~saksoy/courses/cs551/slides/cs551_parametric4.pdf>
Ben-Gal, Irad. “REDES BAYESIANAS”. Departamento de Ingeniería Industrial. Universidad de Tel-Aviv. < http://www.eng.tau.ac.il/~bengal/BN.pdf > http://www.dcs.qmw.ac.uk/~norman/BBNs/BBNs.htm
Charniak, Eugene (1991). “Redes Bayesianas sin Lágrimas”, Revista AI, p. 8.
Friedman, Nir, Linial, Michal, Nachman, Iftach, y Pe'er, Dana. “Uso de redes bayesianas para analizar datos de expresión”. REVISTA DE BIOLOGÍA COMPUTACIONAL, Vol. 7, # 3/4, 2000, Mary Ann Liebert, Inc. pp. 601—620 <www.sysbio.harvard.edu/csb/ramanathan_lab/iftach/papers/FLNP1Full.pdf>
Guo, Haipeng. “Redes Bayesianas Dinámicas”. Agosto de 2002. <www.kddresearch.org/Groups/Probabilistic-Reasoning/258,1, Slide 1>
Neil, Martin, Fenton, Norman y Sastre, Manesh. “Uso de redes bayesianas para modelar pérdidas operativas esperadas e inesperadas”. Análisis de Riesgos, Vol. 25, Núm. 4, 2005 < http://www.dcs.qmul.ac.uk/~norman/papers/oprisk.pdf >
Niedermayer, Daryle. “Una introducción a las redes bayesianas y sus aplicaciones contemporáneas”. 1 de diciembre de 1998. < http://www.niedermayer.ca/papers/bayesian/bayes.html >
Seeley, Rich. “Redes bayesianas fáciles”. Tendencias de Desarrollo de Aplicaciones. diciembre 4, 2007 <www.adtmag.com/article. aspx`id=10271 &page=>.
http://en.Wikipedia.org/wiki/Bayesian_network

Colaboradores y Atribuciones

Autores: Sarah Hebert, Valerie Lee, Matthew Morabito, Jamie Polan

Temperatura	P (Rendimiento = H)	P (Rendimiento = M)	P (Rendimiento = L)
H	0.510.4 + 0.30.6 = 0.384	0.080.4 + 0.20.6 = 0.152	0.410.4 + 0.50.6 = 0.464
M	0.710.4 + 0.920.6 = 0.836	0.090.4 + 0.050.6 = 0.066	0.200.4 + 0.030.6 = 0.098
L	0.210.4 + 0.120.6 = 0.156	0.400.4 + 0.570.6 = 0.502	0.390.4 + 0.310.6 = 0.342

Search

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Ejemplo\(\PageIndex{5}\)