13.4: Regla Bayes, probabilidad condicional e independencia
- Page ID
- 85519
Introducción
La probabilidad es el porcentaje probable de veces que se espera que ocurra un evento si el experimento se repite para un gran número de ensayos. La probabilidad de evento raro es cercana al cero por ciento y la de evento común es cercana al 100%. Contrario a la creencia popular, no se pretende describir con precisión un solo evento, aunque la gente suele usarlo como tal. Por ejemplo, todos sabemos que la probabilidad de ver el lado de la cabeza de una moneda, si la voltearas al azar, es del 50%. No obstante, muchas personas malinterpretan esto como 1 en 2 veces, 2 en 4 veces, 5 en 10 veces, etc. de ver aparecer el lado de la cabeza de la moneda. Entonces, si voltearas una moneda 4 veces y cada vez saliera de cabeza, ¿esta probabilidad del 50% es incorrecta? ¡No! Es solo que el tamaño de tu muestra es pequeño. Si voltearas una moneda 10 mil veces, empezarías a ver una distribución más pareja de cabezas y colas. (Y si no lo haces, probablemente deberías conseguir una moneda diferente). Ahora bien, como ingenieros, aunque sepamos la probabilidad del sistema, no tenemos tiempo para realizar 10 mil pruebas para verificarlo. Sin embargo, se sorprendería de la pequeña cantidad de ensayos que se requieren para obtener una representación precisa del sistema. En las siguientes secciones se describe la relación entre los eventos y sus probabilidades. Estas relaciones serán utilizadas entonces para describir otra teoría de probabilidad conocida como Teorema de Bayes.
Tipos de Probabilidad
Combinación
Combinatoria es el estudio de todos los ordenamientos posibles de un número finito de objetos en distintos grupos. Si utilizamos combinatoria para estudiar las posibles combinaciones hechas a partir del pedido de las letras A, B y C podemos comenzar contando todos los ordenamientos
\[\{(A B C),(A C B), (B C A),(B A C), (C B A),(C A B)\} \nonumber \nonumber \]
dándonos un total de 6 posibles combinaciones de 3 objetos distintos. Como puedes imaginar el método de conteo es sencillo cuando el número de objetos es pequeño pero, cuando el número de objetos que se analizan aumenta el método de contar a mano se vuelve cada vez más tedioso. La forma de hacerlo matemáticamente es utilizando factoriales. Si tienes n objetos distintos entonces puedes ordenarlos en\(n!\) grupos. Desglosando el factorial para nuestro primer ejemplo podemos decir, primero hay 3 objetos para elegir, luego 2, luego 1 sin importar qué objeto elijamos primero. Multiplicando los números juntos obtenemos 3*2*1=3!. Ahora considere encontrar todos los ordenamientos posibles usando todas las letras del alfabeto. Sabiendo que hay 26 letras en el alfabeto inglés, ¡el número de posibles resultados es simplemente 26! , un número tan grande que sería difícil contar.
Ahora, ¿y si hay n objetos y m que son equivalentes y se desea conocer el número de posibles resultados? Por ejemplo, imagina encontrar el número de combinaciones distintas a partir de reorganizar las letras de PIMIENTA. Hay 6 letras, 2 Es y 3 Ps pero solo 1 R. ¡Empezando con 6! tenemos que dividir por los posibles resultados repetidos
\[\dfrac{6 !}{3 ! \times 2 !}=\dfrac{6 \times 5 \times 4 \times 3 !}{3 ! \times 2 !}=\dfrac{6 \times 5 \times 4}{2}= 6 \times 5 \times 2=60 \, \text{possible arrangements} \nonumber \nonumber \]
donde en la parte inferior, el\(3!\) es para los Ps repetidos y el\(2!\) es para los repetidos Es.
Se pueden cancelar los mismos factoriales enteros al igual que los enteros.
El siguiente tema de importancia es elegir objetos de un conjunto finito. Por ejemplo, si cuatro equipos de hockey están formados por 60 jugadores diferentes, ¿cuántos equipos son posibles? Esto se encuentra usando la siguiente relación:
\[ \dfrac{60 \times 59 \times 58 \times 57}{4 \times 3 \times 2 \times 1}=487,635 \, \text{possible teams} \nonumber \nonumber \]
Generalmente, este tipo de problema se puede resolver usando esta relación:
\[(n, r)=\dfrac{n !}{(n-r) ! r !} \label{choose} \]
llamado n elegir r donde\(n\) esta el numero de objetos y\(r\) es el numero de grupos
Usando la ecuación\ ref {choose}, para el ejemplo anterior la matemática sería:
\[ \begin{align*} \dfrac{60 !}{56 ! \times 4 !} &= \\[4pt] \dfrac{60 \times 59 \times 58 \times 57 \times 56 !}{56 ! \times 4 !} &= \\[4pt] \dfrac{60 \times 59 \times 58 \times 57}{4 !} &= 487,635 \, \text{possible teams} \end{align*}\nonumber \]
Probabilidad Conjunta
La probabilidad conjunta es la medida estadística donde se calcula la probabilidad de que dos eventos ocurran juntos y en el mismo punto en el tiempo. Debido a que la probabilidad conjunta es la probabilidad de que dos eventos ocurran al mismo tiempo, solo se puede aplicar a situaciones en las que se pueda hacer más de una observación al mismo tiempo. Al mirar solo dos variables aleatorias,\(A\) y\(B\), esto se denomina distribución bivariada, sin embargo esto se puede aplicar a numerosos eventos o variables aleatorias que se miden a la vez (distribución multivariada). La probabilidad de que dos eventos,\(A\) y\(B\), ambos ocurran se expresa como:
\[P(A, B)\nonumber \]
La probabilidad conjunta también se puede expresar como:
\[P(A \cap B)\nonumber \]
Esto se lee como la probabilidad de la intersección de\(A\) y\(B\).
Si\(A\),\(B\), y\(C\) son variables aleatorias independientes, entonces
\[P(A, B, C)=P(A) P(B) P(C)\nonumber \]
Dos cartas se seleccionan aleatoriamente de una baraja de cartas estándar (sin comodines). Entre cada sorteo la carta elegida es reemplazada de nuevo en la baraja. ¿Cuál es la probabilidad de elegir un cuatro y luego un cinco? Dejar\(P(A)\) denotar la probabilidad de que la primera carta sea un cuatro y\(P(B)\) denotar la probabilidad de que la segunda carta sea un cinco.
Solución
Si hay 52 cartas en una baraja de cartas estándar con 4 trajes, entonces\(P(A)=4 / 52 \) y\(P(B)=4 / 52\). Sabiendo que los eventos son independientes, cada probabilidad se multiplica para encontrar la probabilidad general para el conjunto de eventos. Por lo tanto:
\[\begin{align*} P(A, B) &=P(A) \times P(B) \\[4pt] &= \left(\dfrac{4}{52}\right) \left(\dfrac{4}{52} \right) \\[4pt] &=1 / 169 \end{align*}\nonumber \]
La probabilidad de elegir un cuatro y luego un cinco de la cubierta con reemplazo es 1 de 169.
Probabilidad Condicional
La probabilidad condicional es la probabilidad de que ocurra un evento, dado que ocurre otro evento. La siguiente expresión describe la probabilidad condicional de evento\(A\) dado que ese evento\(B\) ha ocurrido:
\[P(A \mid B)\nonumber \]
Si los eventos A y B son eventos dependientes, entonces se puede usar la siguiente expresión para describir la probabilidad condicional de los eventos:
\[P(A \mid B)=\frac{P(A, B)}{P(B)}\nonumber \]
\[P(B \mid A)=\frac{P(A, B)}{P(A)}\nonumber \]
Esto se puede reorganizar para dar su relación de probabilidad conjunta:
\[\begin{align*} P(A, B) &=P(B \mid A) \times P(A) \\[4pt] &=P(A \mid B) \times P(B) \end{align*}\nonumber \]
Esto establece que la probabilidad de eventos\(A\) y\(B\) ocurrencia es igual a la probabilidad de\(B\) ocurrir dado que\(A\) ha ocurrido multiplicado por la probabilidad de que\(A\) haya ocurrido.
A continuación se muestra una representación gráfica de probabilidad condicional:
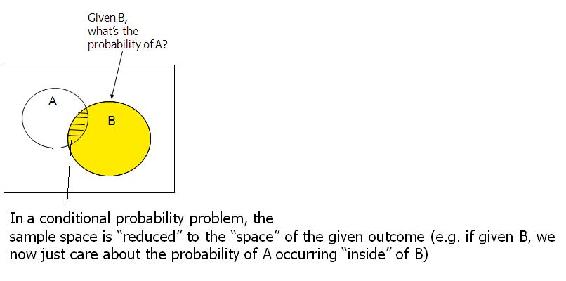
La probabilidad condicional a menudo se deriva de diagramas de árbol o tablas de contingencia. Supongamos que fabrica 100 ejes de pistón. Evento A: la característica A no está defectuosa Evento B: la característica B no está defectuosa
\[P(\text{A Not Def} | \text{B is Def}) = 6 / (80+6) = 0.0698\nonumber \]
\[P(\text{A Not Def} | \text{B Not Def}) = 5 / (9+5) = 0.3571\nonumber \]
Se tiran dos dados justos o imparciales. Algunos resultados de ejemplo son (1,6) y (3,2). La probabilidad de cada posible resultado de los dados es 1/36. Cuando se enrolla el primer dado resulta en un valor de 2. Una vez que se tira el segundo dado, ¿cuál es la probabilidad de que la suma de los dados sea 7?
Solución
Dado que se sabe que el primer valor es 2, la posible combinación de los dos troqueles son los siguientes:
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
Esto da como resultado seis resultados con iguales probabilidades ya que el segundo dado es justo. Por lo tanto, la probabilidad condicional de los resultados anteriores es 1/6. La probabilidad condicional de las 30 combinaciones restantes es 0 ya que el primer dado no es un 2 en estos casos. Por último, dado que solo uno de estos seis resultados puede sumar hasta 7, (2,5), la probabilidad es 1/6 para rodar una suma de 7 dado que el valor del primer dado es un 2.
La probabilidad de que una especie rara de hámster dé a luz a un macho y una hembra es de 1/3. La probabilidad de que el hámster dé a luz a un macho es de 1/2. ¿Cuál es la probabilidad de que el hámster dé a luz a una hembra sabiendo que el hámster ha dado a luz a un macho? Que A denote la probabilidad de dar a luz a un varón y B denota la probabilidad de dar a luz a una hembra.
Solución
- \(P(A\)es la probabilidad de dar a luz a un varón
- \(P(B \mid A\)es la probabilidad de dar a luz a una hembra dado que ya se ha producido el nacimiento de un varón
- \(P(A, A\)es la probabilidad de dar a luz a un varón y una hembra
Estos eventos son dependientes por lo que se debe usar la siguiente ecuación:
\[P(A, B)=P(B \mid A) * P(A)\nonumber \]
Reorganizar esta ecuación para encontrar\(P(B \mid A\) daría:
\[P(B \mid A)=\frac{P(A, B)}{P(A)}\nonumber \]
El enchufar los valores conocidos daría:
\[P(B \mid A)=(1 / 3) /(1 / 2)\nonumber \]
\[P(B \mid A)=2 / 3\nonumber \]
Por lo tanto, la probabilidad de dar a luz a una hembra, dado que el nacimiento de un varón ya ocurrió es de 2/3.
Ley de Expectativa Iterativa
Una aplicación importante de la probabilidad condicional se llama la “Ley de la Expectativa Iterativa” .Dado simplemente, es: E [X] =E [E [X|Y]]. Si se desconoce la distribución de la variable aleatoria de X, pero se nos da la distribución de la variable condicional de X, entonces al encontrar la expección de la variable condicional dos veces, podemos volver a la expectativa de la variable aleatoria original X. Al observar la expectativa de la variable aleatoria X, nosotros puede deducir la distribución de la variable aleatoria X.
La Ley de Expectativa Iterativa es bastante útil en matemáticas y a menudo se utiliza para demostrar relaciones importantes. Tenga en cuenta el siguiente ejemplo:
Utilice la Ley de Expección Iterativa para encontrar Var [X] dado solo X|Y.
Solución
E [Var (X|Y)] = E [X^2] -E [(E [X|Y]) ^2]
Var (E [X|Y)]) =E [(E [X|Y]) ^2] - (E [X]) ^2
E [Var (X|Y)] + Var (E [X|Y]) = E [X^2] -E [(E [X|Y]) ^2] + E [(E [X|Y]) ^2] - (E [X]) ^2
Var [X] = E [(E [X|Y]) ^2] + E [(E [X|Y]) ^2] (por definición)
así Var [X] = E [Var (X|Y)] + Var (E [X|Y])
Probabilidad Marginal
La probabilidad marginal es la probabilidad incondicional de un evento; en otras palabras, la probabilidad de un evento, independientemente de que ocurra otro evento o no. Encontrar la probabilidad marginal de un evento implica sumar todas las configuraciones posibles del otro evento para obtener una probabilidad promedio ponderada. La probabilidad marginal de un evento A se expresa como:
\[P(A)=\sum_{B} P(A, B)=\sum_{B} P(A \mid B) * P(B)\nonumber \]
La probabilidad marginal (de A) se obtiene sumando todas las probabilidades conjuntas. La probabilidad marginal se puede utilizar tanto si los eventos son dependientes como independientes. Si los eventos son independientes entonces la probabilidad marginal se simplifica a simplemente la probabilidad. El siguiente ejemplo aclarará este cómputo.
Las probabilidades conjuntas de lluvia y viento se dan en la siguiente tabla
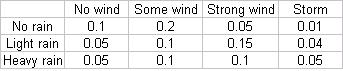
Probabilidad marginal de no lluvia = suma de Probabilidades conjuntas = .1 + .2 + .05+.01 = .36
De igual manera, probabilidad marginal de lluvia ligera = .05+.1+.15+.04 = .34
De igual manera, probabilidad marginal de lluvias fuertes = .3.
Marginar un factor
En un sistema con dos o más factores que afectan la probabilidad de la salida de otro factor, uno de estos factores iniciales puede ser marginado para simplificar los cálculos si ese factor es desconocido.
Por ejemplo, consideremos un sistema donde tanto A como B afectan la salida de C. Si se desconoce la condición de B pero se conoce su probabilidad, se puede marginar para poner el sistema en términos de cómo solo A afecta a C, usando la siguiente ecuación:
\[P(C \mid A)=\sum_{i} P\left(C \mid A, B_{i}\right) P\left(B_{i}\right)\nonumber \]
Ejemplo Problema 2
La siguiente tabla muestra la probabilidad de tener una tormenta de arena grande, pequeña o nula, si hay viento alto, medio o nulo, y dependiendo de si hay lluvia. En la siguiente tabla se muestra la probabilidad de lluvia.
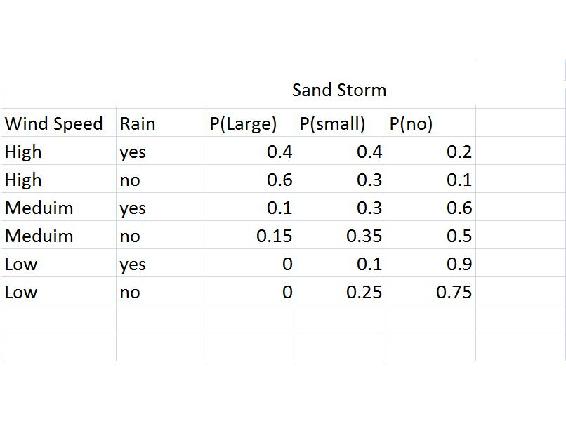
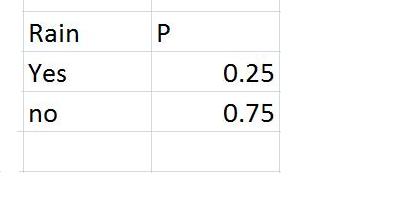
A partir de esto es posible calcular la probabilidad de una tormenta de arena grande, pequeña o ninguna acusada solo en la velocidad del viento:
De manera similar a lo anterior:
P (Tamaño de tormenta de arena|Velocidad del viento) = P (Tamaño de tormenta de arena|Velocidad del Viento, Lluvia) *P (Lluvia) +P (Tamaño Tormenta de Arena|Velocidad del Viento, Sin Lluvia) *P (Sin Lluvia)
Relaciones entre eventos
Saber si dos eventos son independientes o dependientes puede ayudar a determinar qué tipo de probabilidad (conjunta, condicional o marginal) se puede calcular. En algunos casos, la probabilidad de un evento debe calcularse sin saber si se han producido o no eventos relacionados. En estos casos, se debe utilizar la probabilidad marginal para evaluar la probabilidad de un evento.
Independencia
Si los dos eventos se consideran independientes, cada uno puede ocurrir individualmente y el resultado de un evento no afecta el resultado del otro evento de ninguna manera.
Digamos que A y B son eventos independientes. Examinaremos lo que esto significa para cada tipo de probabilidad.
Independencia en Probabilidad Condicional
Los eventos independientes técnicamente no tienen una probabilidad condicional, porque en este caso, A no depende de B y viceversa. Por lo tanto, la probabilidad de A dado que B ya ha ocurrido es igual a la probabilidad de A (y la probabilidad de B dada A es igual a la probabilidad de B). Esto se puede expresar como:
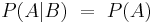
Independencia en probabilidad conjunta
Los eventos independientes pueden tener una probabilidad conjunta, aunque un evento no dependa del otro. Por ejemplo, la probabilidad conjunta se utiliza para describir un evento como lanzar una moneda. El resultado cuando se lanza la moneda la primera vez no está relacionado con el resultado cuando la misma moneda se lanza por segunda vez. Para calcular la probabilidad conjunta de un conjunto de eventos tomamos el producto de las probabilidades individuales de cada evento en el conjunto. Esto se puede expresar como:
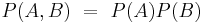
Los eventos independientes también pueden ocurrir en un caso donde hay tres eventos. Por ejemplo, si se están rodando dos dados con una suma de 6 (Evento A). Supongamos que el evento B representa que el primer dado es un 1 y que el evento C representa que el segundo troquel laminado es un 5. Para probar si estos hechos son independientes, se considera la siguiente relación:
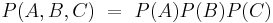
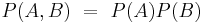
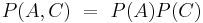
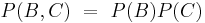
Si alguna de estas relaciones es falsa entonces el evento no es independiente. Al considerar eventos de más de tres, seguiría la misma relación pero con una relación adicional con el evento D.
Dependencia
Si los dos eventos se consideran dependientes, entonces el resultado del segundo evento depende de la probabilidad del primer evento. Las probabilidades de los eventos individuales deben analizarse con probabilidad condicional.
Digamos ahora que A y B son eventos dependientes. Examinaremos lo que esto significa para cada tipo de probabilidad.
Dependencia en Probabilidad Condicional
La probabilidad condicional solo se aplica a eventos dependientes. Es decir, A debe depender de B para determinar la probabilidad de que A ocurra dado que B ya ha ocurrido. Por lo tanto, para los eventos dependientes A y B, solo se pueden aplicar las ecuaciones como se ve en la sección de probabilidad condicional.
\[P(A \mid B)=\frac{P(A, B)}{P(B)}\nonumber \]
y
\[P(B \mid A)=\frac{P(A, B)}{P(A)}\nonumber \]
Dependencia en Probabilidad Conjunta
La probabilidad conjunta también se puede calcular para eventos dependientes. Por ejemplo, la probabilidad conjunta dependiente se puede usar para describir las cartas que se están sacando de una baraja sin reemplazar las cartas después de cada sorteo consecutivo. En este caso, la probabilidad de\(B\) que ocurra\(A\) y suceda es más compleja, ya que la probabilidad de\(B\) que ocurra depende de la probabilidad de\(A\) que suceda. Se puede expresar como:
\[P(A, B)=P(A) P(B \mid A)\nonumber \]
Tenga en cuenta que esta ecuación se encuentra reorganizando la ecuación de probabilidad condicional.
Teorema de Bayes
La mayoría de los problemas de probabilidad no se presentan con la probabilidad de un evento “A”, lo más a menudo es útil condicionar un evento A”.” En otras ocasiones, si se nos da un resultado deseado de un evento, y tenemos varios caminos para alcanzar ese desenlace deseado, el Teorema de Baye demostrará las diferentes probabilidades de que las trayectorias alcancen el desenlace deseado. Conocer cada probabilidad para alcanzar el resultado deseado nos permite escoger el mejor camino a seguir. Así, el Teorema de Baye es de mayor utilidad en un escenario del cual cuando se le da un resultado deseado, podemos condicionar el resultado para darnos las probabilidades separadas de cada condición que conducen al resultado deseado.
El siguiente es el Teorema de Bayes:
\[P\left(B_{j} \mid A\right)=\frac{P\left(A \mid B_{j}\right) P\left(B_{j}\right)}{\sum_{j} P\left(A \mid B_{j}\right) P\left(B_{j}\right)} \label{Bayes} \]
donde\(P\left(A \mid B_{j}\right)\) está\(A\) condicionada la probabilidad de\(B_j\) y\(\sum_{j} P\left(A \mid B_{j}\right) P\left(B_{j}\right)\) es la ley de probabilidad total.
Derivación del teorema de Bayes
La derivación del teorema de Bayes se realiza utilizando la tercera ley de teoría de probabilidad y la ley de probabilidad total.
Supongamos que existe una serie de eventos:\(B_1\)\(B_2\),,...,\(B_n\) y son mutuamente excluyentes; es decir,\(B_{1} \cap B_{2} \cap \ldots \cap B_{n}=0\).
Esto significa que sólo un evento,\(B_j\), puede ocurrir. Tomando un evento “A” del mismo espacio de muestra que la serie de\(B_i\), tenemos:
\[A=\cup_{j} A B_{j}\nonumber \]
Utilizando el hecho de que los eventos\(AB_i\) son mutuamente excluyentes y utilizando la tercera ley de la teoría de la probabilidad:
\[P(A) = \sum_j P(AB_j)\nonumber \]
Condicionando a la probabilidad anterior, el resultado a continuación también se llama “la ley de la probabilidad total”
\[P(A) = \sum_j P(A | B_j)P(B_j)\nonumber \]
Usando la definición de probabilidades condicionales:
\[P\left(B_{j} \mid A\right)=\frac{P\left(A \mid B_{j}\right) P\left(B_{j}\right)}{P(A)}\nonumber \]
Al juntar las dos ecuaciones anteriores, tenemos el Teorema de Bayes (Ecuación\ ref {Bayes}):
\[P\left(B_{j} \mid A\right)=\frac{P\left(A \mid B_{j}\right) P\left(B_{j}\right)}{\sum_{j} P\left(A \mid B_{j}\right) P\left(B_{j}\right)} \nonumber \]
Aplicaciones químicas y del mundo real
La regla de Bayes puede ser utilizada para predecir la probabilidad de una causa dados los efectos observados. Por ejemplo, en la ecuación supongamos que B representa un modelo o hipótesis subyacente y A representa consecuencias o datos observables. Entonces,
\[P(\text {data} \mid \text {model})=\frac{P(\text {model} \mid \text {data}) * P(\text {data})}{P(\text {model})}\nonumber \]
Dónde
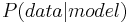: probabilidad de obtener datos observados dado cierto modelo
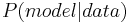: probabilidad de que cierto modelo diera lugar a datos observados
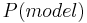: probabilidad de ocurrencia del modelo antes de tomar en cuenta los datos
Otra aplicación: la estimación de la regla de Bayes se utiliza para identificar especies en microscopía de Fluorenscencia de una sola molécula. Puede encontrar más información en [1]
Principios subyacentes y significado de la regla de Bayes
Como se indicó anteriormente, la Regla de Bayes permite cambiar la probabilidad de un evento a partir de nueva información sobre el conocimiento o pericia existente. Por ejemplo, en la subsección anterior la probabilidad de la ocurrencia del modelo, P (modelo), se obtendría a través de muchos ensayos realizados previamente y así se consideraría conocimiento existente. La probabilidad de los datos, P (data), se consideraría entonces nueva información. La Regla de Bayes utiliza esencialmente esta nueva información para actualizar el conocimiento existente y luego determinar la probabilidad de la nueva información con base en el conocimiento existente actualizado. Las estadísticas tradicionales o frecuentistas diferirían de las estadísticas bayesianas al comparar P (datos) con P (modelo) y determinar, con 95% de confianza, si P (datos) es estadísticamente significativo con P (modelo).
La teoría bayesiana está siendo utilizada por muchas empresas e instituciones para clasificar mejor los errores y calcular la incertidumbre. Se ha demostrado que funciona mejor que las técnicas de promediado y se utiliza en sistemas de seguridad así como en estados finales de computación.
Se plantea una pregunta verdadero-falsa a un equipo de dos estudiantes de ChE en un concurso de preguntas. Ambos alumnos elegirán, independientemente, su respuesta. El miembro del equipo A sabe la respuesta correcta, mientras que el miembro del equipo B tiene la respuesta incorrecta. ¿Usa Probabilidad Marginal para encontrar la mejor estrategia para el equipo?
- Estrategia 1: Elige uno de ellos y deja que esa persona responda la pregunta sin saber lo que el otro alumno pensó que era la respuesta correcta.
- Estrategia 2: Que ambos alumnos consideren la pregunta y luego den la respuesta común en la que estén de acuerdo, o si no están de acuerdo, voltee una moneda para determinar qué respuesta dar.
Solución
Estrategia 1
Desglosaremos las diferentes posibilidades para esta situación utilizando las siguientes variables:
- C es el evento de que presenten la respuesta correcta
- A es el evento que el estudiante A es elegido para responder
- B es el evento que el estudiante B es elegido para responder
\[P(C)=P(C, A)+P(C, B)=P(C \mid A) * P(A)+P(C \mid B) * P(B)\nonumber \]
porque existe la misma posibilidad de que cualquiera de los estudiantes sea elegido
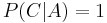porque el estudiante A es correcto
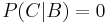porque el estudiante B es incorrecto
\[P(C)=1 *(1 / 2)+0 *(1 / 2)=1 / 2\nonumber \]
\[P(C)=1 / 2\nonumber \]
Estrategia 2
Ya que sabemos que los alumnos no estarán de acuerdo en su respuesta, deben lanzar una moneda para decidir. Por lo tanto la probabilidad es simplemente 1/2.
Ambas estrategias brindan una probabilidad de 1/2 en obtener la respuesta correcta, por lo tanto, son igualmente precisas.
Un biólogo está estudiando células humanas que están infectadas viralmente por una enfermedad mortal, la cual está presente entre 0.01% de la población. Al preparar una muestra, maneja mal un vial con células infectadas y termina por romperse, cortando los guantes protectores y cortando su mano. A pesar de que inmediatamente se lavó las manos, le preocupa que haya contraído la enfermedad. Por suerte para él, su laboratorio ha estado desarrollando una prueba para la enfermedad y ha realizado ensayos con pacientes infectados y no infectados por igual. Entonces, se administra la prueba y para sorpresa del biólogo, la prueba resulta negativa. Se siente aliviado, pero luego recuerda que la prueba no siempre funciona, por lo que decide usar la Regla de Bayes para determinar la probabilidad de que tenga la enfermedad. Entra en la base de datos del laboratorio para obtener todos los datos que necesita para determinarlo.
Solución
Quiere determinar la probabilidad de que dio negativo pero en realidad es positivo para la enfermedad, o\(P(\text { DISpos } \mid \text { TESTneg })\).
De la Regla de Bayes,
\[ P(DISpos|TESTneg) = \frac{P(TESTneg|DISpos)*P(DISpos)}{P(TESTneg)}\nonumber \]
Para encontrar la probabilidad general de una prueba negativa, es necesario usar probabilidad marginal y suma sobre todos los eventos, es decir, tener la enfermedad y no tener la enfermedad:
\[ P(TESTneg) = P(TESTneg|DISpos)*P(DISpos) + P(TESTneg|DISneg)*P(DISneg) \nonumber \]
Suponiendo que todas las personas sin el virus no dan positivo, y que el 99% de los pacientes infectados dan positivo, ¿cuál es la probabilidad de que el biólogo sea realmente positivo con la enfermedad?
\[ P(TESTneg) = .01*.0001 + 1*.9999 = 0.999901 \nonumber \]
\[ P(DISpos|TESTneg) = \frac{(0.01*0.0001)}{.999901}= 1.0001E-06 \nonumber \]
La probabilidad de que el biólogo tenga la enfermedad es de aproximadamente una en un millón.
Si hay 52 cartas en una baraja de cartas estándar con 4 palos, entonces el valor probablemente de escoger una carta de un número particular (5 de espadas, 5 de palos, 5 de diamantes, 5 de corazones) es P (A) = 1/13. La probabilidad asociada con cualquier posterior sorteo de una carta depende únicamente de las cartas restantes en la baraja. Si la misma carta es sacada de la baraja cuatro veces seguidas y no devuelta (resultando en no cincos en la baraja), cuál es la probabilidad de escoger un cuatro, devolverlo a la baraja y luego escoger un 6.
Solución
La probabilidad de cada evento independiente se da a continuación.
\ [\ begin {alineado}
&P (4) =4/48\\
&P (6) =4/48
\ end {alineado}\ nonumber\]
Para encontrar la probabilidad de que ocurran ambos eventos, se debe multiplicar la probabilidad de cada evento independiente.
\[P=P(4) * P(6)=1 / 144 .\nonumber \]
Un jugador tiene dos monedas en el bolsillo, una moneda justa y una moneda de dos cabezas. Toma uno al azar de su bolsillo, lo voltea y consigue cabezas.
- ¿Cuál es la probabilidad de que volteara la moneda justa?
- Si voltea la misma moneda por segunda vez y otra vez recibe cabezas, ¿cuál es la probabilidad de que volteó la moneda justa?
Solución
Llama a F el evento escogió la moneda justa y B el evento escogió la moneda sesgada. Hay dos monedas en su bolsillo por lo que la probabilidad de recoger cualquiera de las dos monedas es de 0.50. Que H_1 sea el evento “el primer volteo es cabezas” y H_2 sea el evento “el segundo flip es cabezas”.
Para (a)
\[P\left(F \mid H_{1}\right)=P\left(H_{1} \mid F\right) * \frac{P(F)}{P\left(H_{1}\right)}=\frac{P\left(H_{1} \mid F\right) P(F)}{P\left(H_{1} \mid F\right) P(F)+P\left(H_{1} \mid B\right) P(B)}\nonumber \]
Dónde y
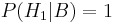, entonces
Para (b)
Esta cuestión se resuelve de la misma manera que a
Considera la situación en la que vas a hacer un recorrido en autobús por la refinería local y la persona que te gusta te ha pedido que los encuentres porque te van a guardar un asiento. Hay tres autobuses que están llevando a los estudiantes de ChEMe en el recorrido y debes decidir de inmediato cuál es el mejor para subir. El primer autobús tiene espacio para 25 estudiantes, el segundo tiene espacio para 45 y el tercero tiene espacio para 55. Para decidir cuál es el mejor autobús, encuentra el valor esperado (o número esperado) de pasajeros para el autobús en el que está tu amigo, dada la siguiente expresión:
\[\mathrm{E}(X)=\sum_{i} x_{i} p\left(x_{i}\right)\nonumber \]
Solución
El valor esperado de X es la suma de los productos de x_i multiplicada por p (x_i)
\[E(passengers)=(25 *(1 / 3)-45 *(1 / 3)+55 *(1 / 3 i)=(25+45+55) / 3=135 / 3=4.5 \nonumber \nonumber \]
Por lo tanto, el número esperado de pasajeros para el autobús en el que está tu amigo es igual a la suma de los pasajeros en cada autobús dividida por el número total de autobuses, asumiendo igual probabilidad de que tu amigo esté en cualquiera de los 3 autobuses. Esto demuestra que debes subir al segundo autobús para poder encontrar a tu amigo.
Método alternativo Ahora considera que no quieres darle a cada autobús la misma oportunidad de que tu amigo esté en él. El objetivo en este método alternativo es encontrar la probabilidad de que tu amigo esté en cada autobús.
\ [\ begin {aligned}
&P (\ text {Bus} 1) =25/135=0.185185\\
&P (\ text {Bus2}) =45/135=0.333333\\
&P (\ text {Bus3}) =55/135=0.407407
\ end {alineado}\ nonumber\]
Ahora usando la nueva probabilidad podemos encontrar un número esperado más preciso de pasajeros en el autobús en el que está tu amigo.
\[E^{\prime}(\text { passengers })=25 *(0.18518)+45 *(0.333333)+55 *(0.407407)=42.037\nonumber \]
Esto muestra un resultado similar, deberías subir al segundo autobús, pero las probabilidades asociadas a cada autobús se ajustan para dar cuenta del número de pasajeros en cada uno.
¿Qué es la probabilidad condicional?
- Una forma de calcular la probabilidad en condiciones variables
- La probabilidad de un suceso, dado que se ha producido otro suceso
- Probabilidad que no se puede determinar
- Probabilidad que siempre es muy pequeña
En la regla de Bayes, ¿qué es P (A)?
- La probabilidad de A
- La probabilidad de A, dada B
- La probabilidad de B, dada A
- La probabilidad marginal de A
- Contestar
-
A
A qué tipo de probabilidad se deduce esta afirmación: ¿Cuál es la probabilidad de que falle un sensor de temperatura dado que un sensor de flujo ha fallado?
- Probabilidad Conjunta
- Probabilidad Condicional
- Probabilidad Marginal
- Contestar
-
B
Referencias
- Ross, Sheldon, Un primer curso en probabilidad: séptima edición, 2006, Pearson Education, Inc.
- Woolf, Keating, Burge, Yaffe, Estadística y cartilla de probabilidad para biólogos computacionales, primavera de 2004, MIT.
- [2] Universidad de Oslo
- [3], Wikipedia