13.14: Muestreo aleatorio de un proceso gaussiano estacionario

Las distribuciones gaussianas son herramientas poderosas para el análisis de datos de muestras generadas aleatoriamente. Las distribuciones gaussianas se asocian típicamente con una “curva Bell”, una representación gráfica de una función de densidad de probabilidad que se caracteriza por un pico en la media de los datos y un ancho determinado por la desviación estándar del conjunto de datos. La distribución de la curva alrededor de la media es simétrica, con ciertos porcentajes de los datos que caen dentro de una desviación estándar de la media. La probabilidad de que exista un punto de datos dentro de un cierto rango de valores es igual al área bajo la curva de densidad de probabilidad entre esos dos valores. El área total bajo la curva es igual a uno porque se puede encontrar que todos los puntos de datos existen en algún lugar de ese conjunto de datos. Para obtener información más detallada sobre las distribuciones gaussianas, consulte la sección Distribuciones Continuas.

El muestreador de números aleatorios es una herramienta poderosa y es muy útil en el modelado de procesos. Un ejemplo de uso de muestreadores de números aleatorios es generar datos meteorológicos a partir de un modelo para simular el cambio climático a lo largo del año, con el fin de mantener adecuadamente la temperatura de un recipiente de almacenamiento. Otra forma en que se puede utilizar es crear un gráfico de control para monitorear qué tan bien se controla un proceso a lo largo del tiempo en base a cierta información sobre el funcionamiento normal del sistema. El objetivo de la generación de números aleatorios es poder utilizar grandes cantidades de datos basados en experimentación limitada para probar un esquema de control.

El objetivo de este artículo es explicar cómo el muestreo aleatorio para formar un conjunto de datos gaussianos es útil en el control de procesos. En primer lugar, se discute cómo utilizar una distribución gaussiana para analizar la probabilidad y comparar las similitudes/diferencias estadísticas entre diferentes conjuntos de datos. Luego hay una explicación de cómo usar el Teorema de Límite Central y mostrar cómo crear una distribución gaussiana a partir de datos no gaussianos usando valores promedio. Los últimos son ejemplos de cómo utilizar esta teoría en los controles de proceso, incluyendo cómo generar y usar gráficos de control.

Muestreador de números aleatorios

El propósito del muestreador de números aleatorios es tomar puntos generados aleatoriamente y convertirlos en una distribución gaussiana (es decir, un PDF). Es importante utilizar puntos distribuidos en todo el rango de 0 a 1. Esta tarea se logra asumiendo que un número aleatorio (\(R\)) es igual al valor 'y' de la función de distribución acumulativa (CDF). El CDF es el área acumulada bajo la curva de la función de densidad de probabilidad (PDF). Al tomar una integral de −∞ a x en el PDF, se puede encontrar este valor 'y' del CDF. Dado que ya se conoce el valor de R, podemos encontrar los\(x\) valores del CDF y así, del PDF. Con los\(x\) valores del PDF conocidos, podemos encontrar\(P(x)\) y construir la distribución gaussiana. La relación entre\(R\) y\(x\) se muestra a continuación:

\ [\ begin {alineado}
R &=\ int_ {-\ infty} ^ {\ frac {x} {2}}\ frac {1} {\ sqrt {2\ pi (\ sigma) ^ {2}}} e^ {\ frac {- (X-\ mu) ^ {2}} {2 (\ sigma) ^ {2}}} d X\
R &= frac {1} {2}\ izquierda [\ nombreoperador {Erf}\ izquierda (\ frac {x-\ mu} {\ sigma\ sqrt {2}}\ derecha) -\ nombreoperador {Erf}\ izquierda (\ frac {-\ infty-\ mu} {\ sigma\ sqrt {2}}\ derecha)\ derecha]\\
R &=\ frac {1} {2}\ izquierda [\ operatorname {Erf}\ izquierda (\ frac {x-\ mu} {\ sigma\ sqrt {2}}\ derecha) +1\ derecha]\\
x &=\ sigma\ sqrt {2}\,\ text {inverseerF} (2 R-1) +\ mu
\ end {alineado}\ nonumber\]

El proceso de elegir un número aleatorio e implementarlo en el PDF se puede hacer usando Mathematica. No se recomienda Excel porque no puede calcular el Erf () de un número negativo, por lo que no podemos usarlo para puntos de datos por debajo de la media en un CDF.

El primer paso para el muestreo aleatorio de un proceso gaussiano estacionario es introducir la media (\(µ\)) y la desviación estándar (\(σ\)) en la siguiente ecuación. Luego, puedes determinar los puntos aleatorios ya sea con la función Random [] en Mathematica o mediante la entrada del usuario para desarrollar una lista de números aleatorios entre 0 y 1. Usando una entrada de número aleatorio como\(R\), Mathematica se puede usar para determinar el punto de datos correspondiente x usando la sintaxis a continuación:

Resolver [R == (1/2) * (Erf [(x- µ)/(σ*SQRT [2])] +1), x]

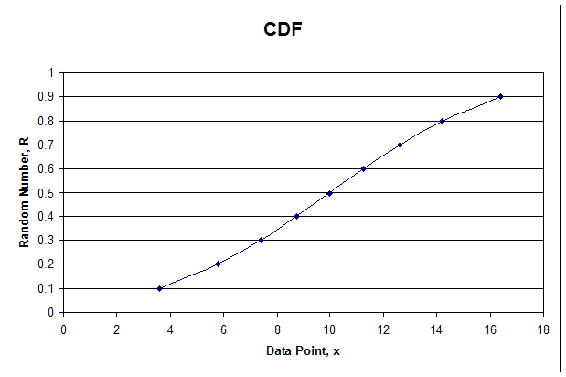
La sintaxis se puede repetir para determinar tantos números aleatorios y sus valores x correspondientes como sea necesario para su problema. Se puede crear una gráfica CDF trazando todos los valores R aleatorios versus sus\(x\) valores correspondientes.

Demostraremos cómo funciona el procedimiento en el siguiente ejemplo. Primero, elegimos 10 números aleatorios y encontramos\(x\) los valores correspondientes, dados en la Tabla 1 con µ = 10 y σ = 5. Ver Figura 1 para la gráfica de la CDF.

Tabla 1: Números aleatorios de CDF y valores x correspondientes

Figura 1: Función de distribución continua

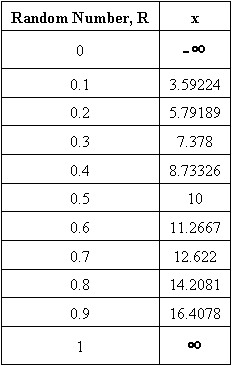
Para desarrollar el PDF ingresaría la media y la desviación estándar en la siguiente ecuación PDF, y encontraría\(P(x)\) para cada valor de x.

\[P(\mu, \sigma)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{\frac{-(X-\mu)^{2}}{2 \sigma^{2}}} \nonumber \]

La sintaxis utilizada en Mathematica es:

Resolver [P (x) == (1/Sqrt [2*pi*σ^2]) *e^ (- (x-µ) ^2/ (2*σ^2)), P (x)]

La sintaxis genera valores para los\(P(x)\) cuales luego se trazan contra los valores x calculados a partir de la CDF. En la siguiente tabla se muestran los números aleatorios generados en Mathematica, los valores x correspondientes y los\(P(x)\) valores para el PDF. A continuación también se muestra la trama del PDF.

Cuadro 2: Para cada R, x Valores y\(P(x)\) Valores Correspondientes

Figura 2: Función de densidad de probabilidad

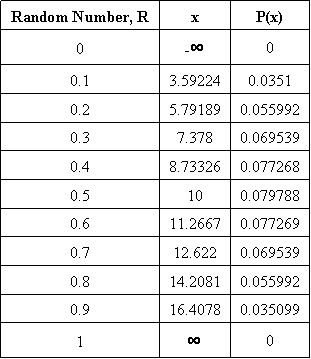
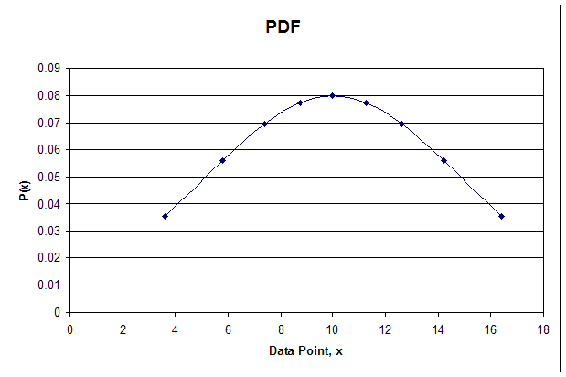
Como pueden ver la trama es de hecho gaussiana. La distribución se volverá más gaussiana a medida que se utilicen más números aleatorios. El mensaje para llevar a casa del generador de números aleatorios es que un conjunto de datos con números que oscilan entre 0 y 1, obtenidos a través de la generación de números aleatorios, se puede convertir en una distribución gaussiana.

Cebadores de probabilidad

Una ventaja importante del muestreador de números aleatorios es la capacidad de generar diferentes conjuntos de datos sin tener que recopilar datos realmente. Estos conjuntos de datos se pueden utilizar para ayudarle a comprender mejor el funcionamiento de muchas de las diferentes comparaciones estadísticas. Por ejemplo, si el tamaño de la muestra aumenta, ¿eso lleva a más o menos significancia en la diferencia de dos medias? La mayoría de estas herramientas de análisis son temas de otras wikis, por lo que volveremos a visitar algunas solo brevemente con la intención de hacer preguntas más profundas en el ejemplo 1.

Probabilidad

Recordemos que el área bajo cualquier función gaussiana está relacionada con la probabilidad. Supongamos que usamos nuestro muestreador para generar un conjunto aleatorio de 100 puntos de datos con una media de 10 y una desviación estándar de 5. La probabilidad de crear un punto de datos adicional entre 'a' y 'b' es la integral de la función de distribución gaussiana de 'a' a 'b' de la siguiente manera:

\[P(a \leq x \leq b)=\int_{a}^{b} \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{\frac{-(x-\mu)^{2}}{2 \sigma^{2}}} d x \nonumber \]

Se puede encontrar más información sobre las probabilidades en la sección de Distribuciones Continuas.

Error en la media

Supongamos que tenemos el mismo conjunto de datos descrito anteriormente. Digamos que deseamos agregar un nuevo punto de datos y calcular la probabilidad de que la nueva media del conjunto de datos se encuentre entre 'c' y 'd'. Este cálculo es muy similar al descrito anteriormente con una diferencia. La desviación estándar, que describe la varianza en puntos de datos individuales, se reemplaza por el error estándar en la media, que describe la varianza en la media a medida que cambia el tamaño de la muestra de datos. El error estándar en la media se calcula de la siguiente manera:

\[\sigma_{\mu}=\frac{\sigma}{\sqrt{n}} \nonumber \]

Una vez obtenido este valor, podemos resolver para la probabilidad de la siguiente manera:

\[P(a \leq \mu \leq b)=\int_{c}^{d} \frac{1}{\sqrt{2 \pi \sigma_{\mu}^{2}}} e^{\frac{-(x-\mu)^{2}}{2 \sigma_{\mu}^{2}}} d x \nonumber \]

Se puede encontrar más información sobre el error estándar en la sección de Comparación de Dos Medias.

Comparación de dos conjuntos de datos

Ahora supongamos que tenemos dos conjuntos de datos distintos con diferentes medias y desviaciones estándar y deseamos determinar si un conjunto de datos es estadísticamente diferente del segundo. Para ello, calcularemos un valor p. El valor p se calcula de la siguiente manera:

\ [\ begin {array} {l}
P\ left (\ mu_ {1}\ fila derecha\ mu_ {2},\ mu_ {1} <\ mu_ {2}\ derecha) =\ int_ {m} ^ {\ infty}\ frac {1} {\ sqrt {2\ pi\ sigma_ {\ mu 1} ^ {2}} e^ {\ fr{ - (x-\ mu) ^ {2}} {2\ sigma_ {\ mu 1} ^ {2}}} d x\\
P\ izquierda (\ mu_ {1}\ fila derecha\ mu_ {2},\ mu_ {1} >\ mu_ {2}\ derecha) =\ int_ {-\ infty} ^ {m}\ frac {1}\ sqrt {2\ pi\ sigma_ {\ mu 1} ^ {2}}} e^ {\ frac {- (x-\ mu) ^ {2}} {2\ sigma_ {\ mu 1} ^ {2}}} d x
\ end {array}\ nonumber\]

Puede encontrar más información sobre los valores p y las comparaciones de medias en estos artículos wiki: Comparación de dos medias y valores P

Teorema de Límite Central

Recordemos que una propiedad del muestreador de números aleatorios fue que a medida que aumentaba el conjunto de números generados aleatoriamente, los errores se volvían más aleatorios y la distribución se volvía más gaussiana. El teorema del límite central establece que el muestreo de una media de distribución dada se acercará a una distribución normal o gaussiana a medida que aumenta el tamaño de la muestra. Este teorema es probado por el siguiente ejemplo ilustrado en la “Estadística para Experimentadores: Una Introducción al Diseño, Análisis de Datos y Construcción de Modelos”.

Rolling de dados

La probabilidad de que cierta cara aterrice erguida al rodar un dado de seis lados es la misma para cada cara. Esto se muestra a continuación en la Figura 3 (a). El valor medio de un rollo se puede calcular para ser 3.5 sumando el valor de cada cara y dividiendo por 6. A medida que se incrementa el tamaño de la muestra, se demostrará que este valor medio tiene la mayor densidad de ocurrencia. Cuando el tamaño de la muestra se incrementa a dos dados se puede notar en la Figura 3 (b) que la distribución de densidad de la puntuación promedio comienza a tomar la forma de una curva. La distribución de densidad de la puntuación promedio para el tamaño de la muestra aumenta a tres, cinco y diez dados se muestran en la Figura 3 (c, d y e respectivamente). Por cada incremento se puede observar que la densidad de los valores extremos disminuye y la distribución global de la densidad aparece más como una distribución gaussiana, como lo predice el teorema del límite central.

Figura 3: Distribución a partir del aumento del tamaño de la muestra (Caja, “Estadística para Experimentadores”)

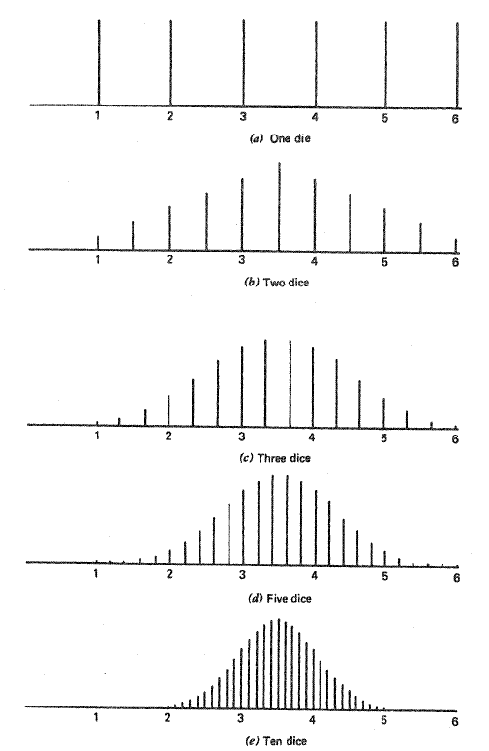
Generación de números aleatorios

El ejemplo de dados anterior es análogo a la generación de números aleatorios. Considera un conjunto de números aleatorios entre 0 y 10. Si estos números fueran realmente elegidos al azar, entonces se esperaría una distribución uniforme de números entre 0 y 10. El promedio de estos números sería de alrededor de 5, con una gran desviación estándar. Sin embargo, supongamos que su conjunto de datos ahora consiste en un promedio de dos números aleatorios. En este caso, los datos se distribuirán de manera menos uniforme, ya que el promedio tiende a disminuir la contribución de términos más alejados de 5. La forma de la distribución comenzará a aparecer gaussiana.

A medida que aumenta el número de números aleatorios promediados juntos ('n') para crear cada punto de datos, la distribución se vuelve de naturaleza más gaussiana. Por favor refiérase a la figura 4. Cuando n=1 (se usa un número aleatorio para calcular cada punto de datos), la distribución de densidad es relativamente uniforme. A medida que 'n' aumenta, las curvas se vuelven de naturaleza más gaussiana hasta que tenemos una distribución gaussiana muy suave cuando n=100 (se promediaron 100 números aleatorios para obtener un punto de datos).

Figura 4: Distribución de puntos de datos generados promediando números aleatorios

Ejemplo\(\PageIndex{1}\)

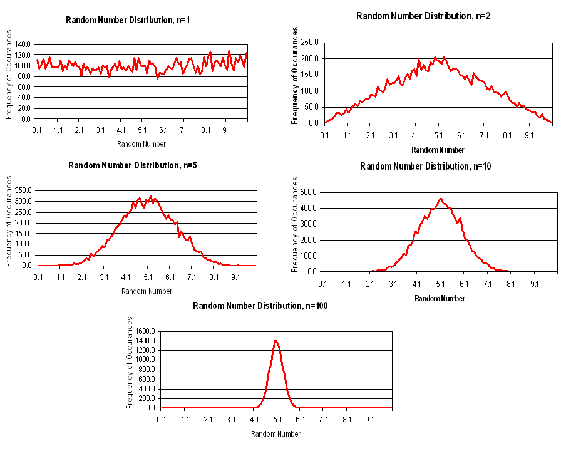
En una hembra adulta sana, estudios han demostrado que la fracción media de sangre desoxigenada que sale de los pulmones es de 0.05 con una desviación estándar 0.01. Para obtener estos datos, se habían muestreado 100 hembras sanas utilizando nuestro muestreador de números aleatorios.

1. Asumiendo que esta distribución es gaussiana, el 95% de todas las hembras sanas tendrán fracciones de sangre desoxigenadas en qué rango (supongamos que este rango está centrado sobre la media de los datos)?
2. ¿Cuál es el error esperado en la media a un nivel de confianza del 95%?
3. Se ha realizado un segundo estudio en hembras adultas gestantes. Se encontró que la fracción media de sangre desoxigenada que salía de los pulmones fue de 0.06 con una desviación estándar de 0.02. ¿La concentración sanguínea desoxigenada en esta población de mujeres es estadísticamente diferente?
4. Ahora supongamos que sólo se habían muestreado 10 hembras adultas en lugar de 100. Analizar cómo puede cambiar la respuesta a la parte (c).

Solución

a) Para resolver este problema, recordar la ecuación de una distribución gaussiana. Sustituir en el valor de la media (0.05) y desviación estándar (0.01). A continuación, recordemos que el área bajo la curva corresponde a probabilidad, por lo que podemos establecer integrar esta función para determinar el rango en el que la probabilidad es igual a 0.95. Los límites en esta integral son 0.05 + k y 0.05 — k, ya que estamos asumiendo que este rango de datos está centrado alrededor de la media. Esta integral se puede resolver en forma integral o en forma de función de error, dependiendo de los comandos que elija usar para ingresar la función en un solucionador de sistemas de álgebra computacional. Maple, Excel y Matemáticas se pueden usar para resolver la expresión simplemente ingresando la última línea del texto matemático que se muestra en la solución a continuación.

\ [\ begin {array} {l}
P (\ mu,\ sigma) =\ frac {1} {\ sqrt {2\ pi\ sigma^ {2}}} e^ {\ frac {- (x-\ mu) ^ {2}} {2\ sigma^ {2}}}\\
P (\ mu,\ sigma) =\ frac {1} {\ sqrt {2\ pi (0.01) ^ {2}}} e^ {\ frac {- (x-0.05) ^ {2}} {2 (0.01) ^ {2}}}\\
0.95=\ int_ {005-k} ^ {005+k}\ frac {1} {\ sqrt {2\ pi (0.01) ^ {2}}} e^ {\ frac {- (x -0.05) ^ {2}} {2 (001) ^ {2}}} d x\
0.95=\ frac {1} {2}\ left [\ operatorname {Erf}\ left (\ frac {0.05+k-0.05} {0.01\ sqrt {2}}\ right) -\ operatorname {Erf}\ left (\ frac {0.05-k-0.05} {0.01\ sqrt {2}}\ derecha)\ derecha]\
k=0.02
\ end {array}\ nonumber\]

Por lo tanto, 95% de las hembras adultas sanas tienen niveles sanguíneos desoxigenados entre 0.03 y 0.07.

b) Este problema se resuelve mucho de la misma manera que resolvimos la parte (a). Sin embargo, en este caso estamos buscando el intervalo de confianza del 95% de la media, y no toda la población. Por lo tanto, la desviación estándar debe convertirse al error estándar en la media. Entonces, se repiten todos los cálculos anteriores.

\ [\ begin {alineado}
&\ sigma_ {\ mu} =\ frac {\ sigma} {\ sqrt {n}} =\ frac {0.01} {\ sqrt {100}} =0.001\\
&P\ izquierda (\ mu,\ sigma_ {\ mu}\ derecha) =\ frac {1} {\ sqrt {2\ pi (0.001) ^ {2}} e^ {\ frac {- (x-0.05) ^ {2}} {2 (0.001) ^ {3}}}\\
&0.95=\ int_ {0.05-k} ^ {0.05+k}\ frac {1} {\ sqrt {2\ pi (0.001) ^ {2}} } e^ {\ frac {- (x-0.09) ^ {2}} {2 (0.001) ^ {2}}} d x\\
&0.95=\ frac {1} {2}\ left [\ operatorname {Erf}\ left (\ frac {0.05+k-0.05} {0.001\ sqrt {2}}\ right) -\ operatorname {Erf} left\ (\ frac {0.05-k-0.05} {0.001\ sqrt {2}}\ derecha)\ derecha]\\
&k=0.002
\ end {alineado}\ nonumber\]

Por lo tanto, el intervalo de confianza del 95% de la media es 0.05 ± 0.002.

c) Para comparar la significancia estadística de dos conjuntos de datos diferentes, se debe utilizar el concepto de valores p. Dado que nos interesa comparar las medias de estos dos conjuntos de datos, la desviación estándar será reemplazada por el error estándar en la media. Para encontrar la probabilidad (o valor p) de que el embarazo resulte en niveles más altos de sangre desoxigenada, necesitamos calcular el área bajo la curva gaussiana para mujeres sanas que es de 0.06 o más. Recuerde, estamos evaluando la función gaussiana describiendo hembras sanas, por lo que no se necesitan datos de desviación estándar para las hembras gestantes.

\ [\ begin {alineado}
&\ sigma_ {\ mu} =\ frac {\ sigma} {\ sqrt {n}} =\ frac {0.01} {\ sqrt {100}} =0.001\\
&P\ izquierda (\ mu,\ sigma_ {\ mu} ^ derecha) =\ frac {1} {\ sqrt {2\ pi\ sigma_ {\ mu} {2}}} e^ {\ frac {- (x-\ mu) ^ {2}} {2\ sigma_ {k} ^ {2}}}\\
&P\ izquierda (\ mu,\ sigma_ {\ mu}\ derecha) =\ frac {1} {\ sqrt {2\ pi (0.001) ^ {2}}} e^ {\ frac {- (x-005) ^ {2}} {2 (0.001) ^ {2}}}\\
&P (x\ geq 0.06) =\ int_ {0.06} ^ {\ infty}\ frac {1} {\ sqrt {2\ pi (0.001) ^ {2}} e^ {\ frac {- (x-0.05) ^ {2}} {2 (0.001) ^ {1}}} d x\\
&P (x\ geq 0.06) =\ frac {1} {2}\ izquierda [\ operatorname {Erf}\ izquierda (\ frac {\ infty-0.05} {0.001\ sqrt {2}}\ derecha) -\ nombreoperador {Erf}\ izquierda (\ frac {0.06-0.05} {0.001\ sqrt {2}}\ derecha)\ derecha]\\
&P (x\ geq 0.06) =\ frac {1} {2}\ izquierda [1-\ operatorname {Erf}\ izquierda (\ frac {0.06-0.05} {0.001\ sqrt {2}}\ derecha)\ derecha]\\
&P (x\ geq 0.06) =0
\ end {alineado}\ nonumber\]

El valor p es igual a cero. Por convención, los valores p menores a 0.05 se consideran estadísticamente significativos. Por lo tanto, concluimos que el embarazo afecta estadísticamente el nivel de sangre desoxigenada en el cuerpo de una mujer adulta.

d) El tamaño de la muestra sólo incide en el error estándar en la media. Para resolver este problema, recalcular el error estándar y repetir los cálculos anteriores.

\ [\ begin {alineado}
&\ sigma_ {\ mu} =\ frac {\ sigma} {\ sqrt {n}} =\ frac {0.01} {\ sqrt {10}} =0.003\\
&P\ izquierda (\ mu,\ sigma_ {\ mu}\ derecha) =\ frac {1} {\ sqrt {2\ pi\ sigma_ {\ mu} ^ {2}}} e^ {\ frac {- (x-\ mu) ^ {2}} {2} {2\ sigma_ {k} ^ {2}}}\\
&P\ izquierda (\ mu,\ sigma_ {\ mu}\ derecha) =\ frac {1} {\ sqrt {2\ pi (0.003) ^ {2}}} e^ {\ frac {- (x-0.09) ^ {3}} {2 (0000) ^ {2}}}\\
&P (x\ geq 0.06) =\ int_ {0.06} ^ {\ infty}\ frac {1} {\ sqrt {2\ pi (0.003) ^ {2}} e^ {\ frac {\ {- (x-0.00) ^ {2}} {2 (0.003) ^ {2}}} d x\\
&P (x\ geq 0.06) =\ frac {1} {2}\ left [\ operatorname {Erf}\ left (\ frac {\ infty-0.05} {0.003\ sqrt {2}}\ derecha) -\ operatorname {Erf}\ izquierda (\ frac {0.06-0.05} {0.003\ sqrt {2}}\ derecha)\ derecha]\\
&P (x\ geq 0.06) =\ frac {1} {2}\ left [1-\ operatorname {Erf}\ left (\ frac {0.06-0.05} {0.003\ sqrt {2}}\ right)\ derecha]\\
&P (x\ geq 0.06) =0.0004
\ end {alineado}\ nonumber\]

En este caso, el valor p sigue siendo inferior a 0.05, por lo que seguimos llegando a la misma conclusión. También concluimos que a medida que disminuye el tamaño de la muestra, las diferencias en las medias de la muestra se vuelven menos significativas porque el valor p ha aumentado ligeramente.

Ejemplo\(\PageIndex{2}\): Comparison of Two Data Sets

Este ejemplo pretende demostrar cómo el aumento del tamaño de la muestra afecta a la comparación de dos conjuntos de datos.

Usando un generador de números aleatorios, se generaron cuatro conjuntos de datos (A, B, C, D). Cada conjunto de datos contiene 100 puntos de datos totales. Para los conjuntos de datos A y B, se promediaron dos números aleatorios para alcanzar cada punto de datos, mientras que en C y D, se promediaron cinco números aleatorios para cada punto. Esta diferencia resultó en desviaciones estándar más pequeñas para los conjuntos de datos C y D. En el siguiente gráfico se muestra un resumen de los cuatro conjuntos de datos creados. M es el número de muestras aleatorias promediadas para obtener cada punto de datos. N es el número total de puntos de datos. También se da la media y desviación estándar para cada uno de los conjuntos de datos.

1. Comparar las medias de los conjuntos de datos A y B calculando el valor p
2. Comparar las medias de los conjuntos de datos C y D calculando el valor p
3. Comparar los valores p obtenidos para las partes a) y b) anteriores. Explique por qué los valores tienen sentido.
4. ¿Qué efecto general tiene el aumento del tamaño de la muestra en la comparación de dos conjuntos de datos?

Solución

a) El valor p que compara los conjuntos de datos A y B se calcula de la siguiente manera:

\ [\ begin {alineado}
&\ sigma_ {\ mu} =\ frac {\ sigma} {\ sqrt {n}} =\ frac {2.3} {\ sqrt {100}} =0.23\\
&P\ izquierda (\ mu,\ sigma_ {\ mu}\ derecha) =\ frac {1} {\ sqrt {2\ pi\ sigma_ {\ mu} ^ {2}}} e^ {\ frac {- (x-\ mu) ^ {2}} {2} {2\ sigma_ {k} ^ {2}}}\\
&P\ izquierda (\ mu,\ sigma_ {\ mu}\ derecha) =\ frac {1} {\ sqrt {2\ pi ( 0.23) ^ {2}} e^ {\ frac {- (x-5) ^ {2}} {2 (0.23) ^ {2}}}\\
&P (x\ geq 5.5) =\ int_ {55} ^ {\ infty}\ frac {1} {\ sqrt {2\ pi (0.23) ^ {2}} e^ {\ frac - {(x-5) ^ {3}} {2 (0.23) ^ {3}}} d x\\
&P (x\ geq 5.5) =\ frac {1} {2}\ left [\ operatorname {Erf}\ left (\ frac {\ infty-5} {0.23\ sqrt {2}}\ right) -\ operatorname {Erf}\ left (\ frac {5.5-5} {0.23\ sqrt {2}}\ derecha)\ derecha]\\
&P (x\ geq 5.5) =\ frac {1} {2}\ izquierda [1-\ operatorname {Erf}\ izquierda (\ frac {5.5-5} {0.23\ sqrt {2}}\ derecha)\ derecha]\\
&P (x\ geq 5.5) =0.015
\ final {alineado}\ nonumber\]

A partir de este valor p, podemos ver que es muy poco probable que estos dos conjuntos de datos sean estadísticamente iguales. ¡Solo hay un 1.5% de probabilidad de obtener aleatoriamente un conjunto de datos con una media tan alta como 5.5! Es mucho más probable que estos dos conjuntos de datos sean en realidad estadísticamente diferentes.

b) El valor p que compara los conjuntos de datos C y D se calcula de la siguiente manera:

\ [\ begin {alineado}
&\ negridsymbol {\ sigma} _ {\ mu} =\ frac {\ negridsymbol {\ sigma}} {\ sqrt {n}} =\ frac {1.1} {\ sqrt {100}} =0.11\\
&P\ izquierda (\ mu,\ sigma_ {\ mu}\ derecha) =\ frac {1} {\ sqrt {2\ pi\ sigma_ {\ mu} ^ {2}}} e^ {\ frac {- (x-\ mu) ^ {2}} {2\ sigma_ {F} ^ {2}}}\\
&P\ izquierda (\ mu,\ sigma_ {\ mu}\ derecha) =\ frac {1} {\ sqrt {2\ pi (0.11) ^ {2}}} e^ {\ frac {- (x-5) ^ {3}} {2 (0.11) ^ {2}}}\\
&P (x\ geq 5.5) =\ int_ {5.5} ^ {\ infty}\ frac {1} {\ sqrt {2\ pi (0.11) ^ {2}}} e^ {\ frac {- (x-5) ^ {2}} {2 (0.11) ^ {3}}} d x\\
&P (x\ geq 5.5) =\ frac {1} {2}\ left [\ operatorname {Erf}\ left (\ frac {\ infty-5} {0.11\ sqrt {2}}\ derecha) -\ operatorname {Erf}\ izquierda (\ frac {5.5-5} {0.11\ sqrt {2}}\ derecha)\ derecha]\\
&P (x\ geq 5.5) =\ frac {1} {2}\ left [1-\ operatorname {Erf}\ left (\ frac {5.5-5} {0.11\ sqrt {2}}\ derecha)\ derecha]\\
&P (x\ geq 5.5) =0
\ end {alineado}\ nonumber\]

A partir de este valor p, podemos ver que estos dos conjuntos de datos son estadísticamente diferentes. ¡Hay una probabilidad de casi 0 por ciento de obtener aleatoriamente un conjunto de datos con una media tan alta como 5.5!

c) Comparando los dos valores p, podemos ver que el valor para b) es menor que a), lo que indica que tenemos más confianza en una diferencia estadística entre los conjuntos C y D que entre A y B. Volviendo a la descripción del problema, podemos encontrar una razón para este resultado. Debido al mayor muestreo de números aleatorios en los conjuntos de datos C y D (cinco números promediados para cada punto de datos, en comparación con solo dos), estos conjuntos de datos tienen desviaciones estándar más pequeñas. Estas desviaciones estándar más pequeñas significan que tenemos un mayor nivel de confianza de que la media de la muestra es la media verdadera. Debido a que cada conjunto de datos es más probable que muestre la media verdadera, también hay una mayor probabilidad de que un conjunto de datos sea estadísticamente diferente del otro.

d) En una distribución gaussiana, a medida que aumenta el tamaño de la muestra, disminuye el error estándar. Esto indica que la media de la muestra está más cerca de la media real, y es más probable que dos conjuntos de datos sean estadísticamente diferentes entre sí que si hay tamaños de muestra más pequeños y desviaciones estándar más altas en los conjuntos de datos.

Gráficas de control

Esta sección proporcionará una breve descripción de los gráficos de control para completar el ejemplo 3, en el que nuestro muestreador de números aleatorios se aplica a una situación de gráfico de control. Para una explicación más detallada sobre los gráficos de control, y la metodología detrás de ellos, por favor vea esta página wiki: Gráficos de control

Antecedentes

Los gráficos de controles son herramientas que se utilizan para determinar si una parte particular de un proceso es predecible o no. Un proceso es predecible cuando se encuentra en un estado de control estadístico e impredecible cuando no está en un estado de control estadístico. Un estado de control estadístico simplemente significa que podemos predecir con precisión cuál será el resultado de un proceso en el futuro con base en mediciones pasadas; no significa que el producto esté en el objetivo o dentro de cualquier límite de aceptabilidad del consumidor. El muestreador de números aleatorios es una herramienta útil que se puede utilizar para analizar gráficos de control. Como se discutió anteriormente, un conjunto de datos es de naturaleza más gaussiana a medida que aumenta la cantidad de puntos de datos. Por lo tanto, uno esperará que un gran conjunto de datos generados con nuestro muestreador de números aleatorios siempre esté en control estadístico, pero conjuntos más pequeños pueden contener un elemento de imprevisibilidad.

Para crear una tabla de control, comenzamos por observar las mediciones de datos históricos sobre la medición (variable) de importancia, por ejemplo, la concentración de ácido acético. Una vez que se ha recopilado una cantidad razonable de datos, se utiliza para calcular los límites apropiados para la variable. Si los datos históricos y las mediciones futuras caen dentro del rango de los límites, es seguro predecir que las mediciones futuras también seguirán estando dentro del rango de los límites. Por el contrario, si los datos históricos no caen dentro del rango de los límites, se puede predecir con seguridad que las mediciones futuras no caerán dentro del rango de los límites.

Construcción de gráficos de control

La mejor manera de ilustrar cómo crear un gráfico de control es pasar por un ejemplo. Esto se hace a continuación. La suposición inicial al desarrollar un gráfico de control es que el proceso es estable durante un período de tiempo donde se puede realizar un conjunto de mediciones sobre una variable particular del proceso. En el siguiente ejemplo, esta variable es la concentración de ácido acético.

Ejemplo\(\PageIndex{1}\)

Los ingenieros químicos a menudo combinan anhídrido acético y agua para producir ácido acético en una reacción moderadamente exotérmica. Se supone que la reacción en este proceso particular produce una corriente de producto de ácido acético al 5.5% en peso. La composición de la corriente de producto se mide cuatro veces cada hora durante diez horas. Las mediciones de cada hora se ven como un subgrupo de datos. En el Cuadro 1 se muestran los datos obtenidos de las 40 mediciones. En el Cuadro 1 también se enumeró la concentración promedio y el rango de concentraciones para cada subgrupo de mediciones.

Cuadro 3. Datos de muestra - Concentración de ácido acético

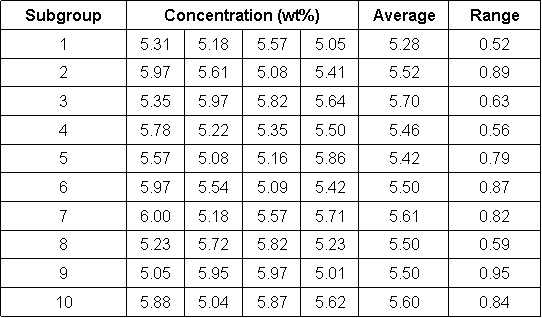
Para crear un gráfico de control para este proceso, primero debemos calcular la concentración promedio para cada subconjunto. Adicionalmente, debemos determinar el rango de datos para cada subconjunto. Estos pasos ya se completaron y sus valores se listan en la Tabla 3 en las dos últimas columnas de la derecha. A continuación, la concentración promedio y el rango promedio deben calcularse promediando las concentraciones promedio de cada subconjunto y tomando el promedio de los rangos de cada subconjunto. Para los datos del cuadro 3, la concentración promedio general es de 5.51% en peso y el rango promedio es de 0.74% en peso. En este punto, estamos listos para determinar nuestros límites de control superior e inferior para nuestra concentración de ácido acético. Para determinar estos límites necesitaremos usar una tabla de constantes que se han derivado matemáticamente para distribuciones gaussianas. Estos números se pueden insertar en ecuaciones que encuentran los límites de control promedio superior e inferior (UCL _x y LCL _x) y los límites de control de rango superior e inferior (UCL _R y LCL _R). Las siguientes ecuaciones proporcionan los límites de control para las concentraciones promedio y para sus rangos.

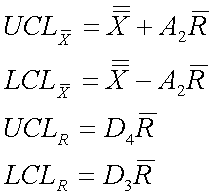
Cuadro 5. Constantes para gráficos de promedio y rango basados en el rango promedio

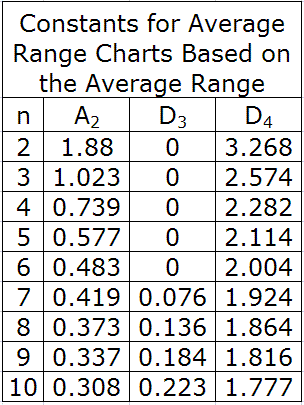
Para este ejemplo, nuestro tamaño de subgrupo, n, es 4, A2 es 0.729, D3 es 0 y D4 es 2.282. Cuando están conectados a las ecuaciones anteriores, producen límites de control de:

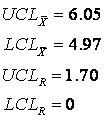
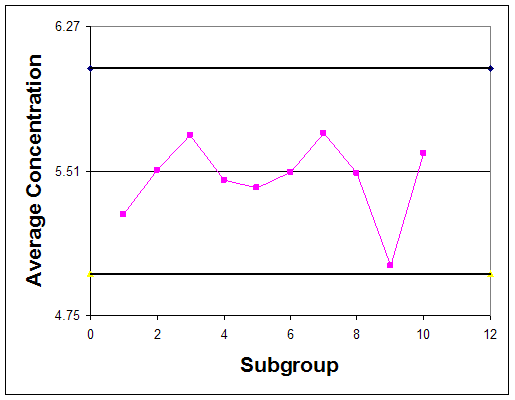
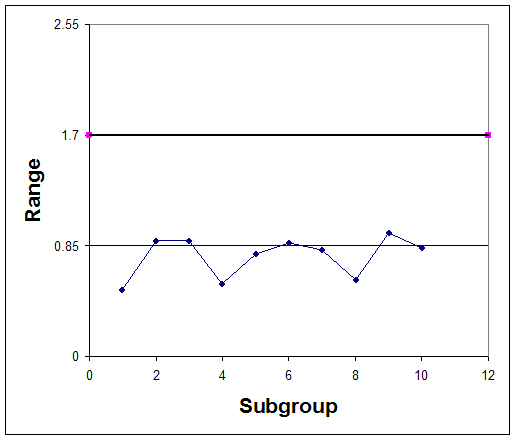
Gráficamente, el gráfico de control se representa creando una gráfica de los valores de concentración promedio versus su número de subgrupo y creando una gráfica de cada valor de rango versus el número de subgrupo. Se deben incluir líneas horizontales en estas parcelas que indiquen los límites de control. Los gráficos de control para este ejemplo se trazan en las figuras 3 y 4.

Figura 6. Tabla de control para la concentración promedio de ácido acético

Figura 7. Tabla de control para rangos de concentración de ácido acético

Interpretación de gráficos de control

Si alguna de las siguientes reglas es cierta para la tabla de control de centrado, el proceso no está en control estadístico.

1. Uno o más puntos quedan fuera de los límites de control.
2. Siete o más puntos consecutivos caen en el mismo lado de la línea central.
3. Diez de 11 puntos consecutivos caen del mismo lado de la línea central.
4. Tres o más puntos consecutivos caen en el mismo lado de la línea central y todos están ubicados más cerca del límite de control que de la línea central.

Observe que tanto en la tabla de control para las concentraciones promedio, los datos históricos nunca superan o van por debajo de los límites de control. Además, ninguna de las otras reglas anteriores es cierta para este gráfico. Esto sugiere que el proceso es estable; sin embargo, para confirmar este pensamiento, se deben hacer observaciones futuras. Si la concentración promedio de ácido acético y su rango continúan manteniéndose dentro de los límites de control, se dice que el proceso es estable.

En el caso de que los datos históricos no permanecieran dentro de los límites de control, las parcelas podrían haberse parecido a las figuras 5 y 6.

Figura 8. Tabla de control para la concentración promedio de ácido acético (inestable)

Figura 9. Tabla de control para rangos de concentración de ácido acético (inestable)

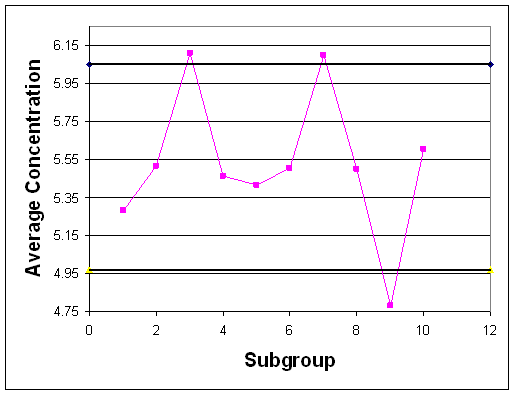
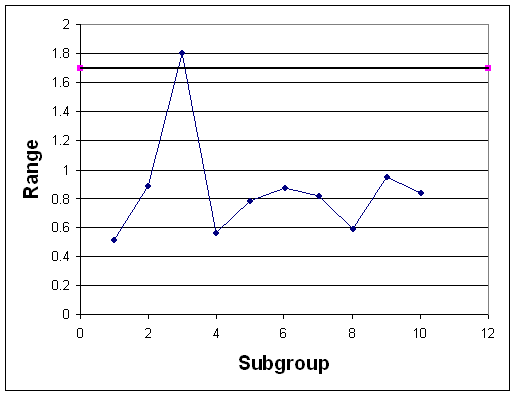
Observe que en cada una de estas gráficas de control, los datos históricos no permanecen dentro de los límites de control para el proceso. Con base en esta observación, se puede predecir que los datos futuros tampoco permanecerán dentro de los límites de control para el proceso y el proceso no es estable. En conclusión, los gráficos de control permiten utilizar muestras de datos para determinar los límites de control para un proceso y evaluar si el proceso es estable o no.

Ejemplo\(\PageIndex{1}\): Random Sampling Problem

En un proceso de bioingeniería industrial, se desea obtener una relación de 75% de prolina a 25% de hidroxiprolina en una enzima especializada. Las composiciones relativas pueden analizarse usando un colorante fluorescente, donde una fluorescencia de 10 corresponde a la proporción correcta de estos dos aminoácidos. Para monitorear la estabilidad de este proceso, se toman cinco lecturas cada 30 minutos durante el proceso de producción de 10 horas. Los resultados se obtuvieron utilizando nuestro muestreador de números aleatorios con una media especificada (10) y desviación estándar (en este caso 1.6). Los resultados están en la tabla siguiente

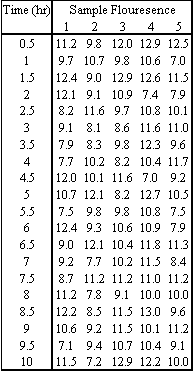
1. Calcular el promedio y el rango para cada subgrupo de datos.
2. Cree un gráfico de promedio y rango para todo el tiempo de producción.
3. ¿Este proceso está en control?

Solución

El promedio y el rango se pueden calcular usando las funciones =PROMEDIO () y =MAX () -MIN () de Microsoft excel.

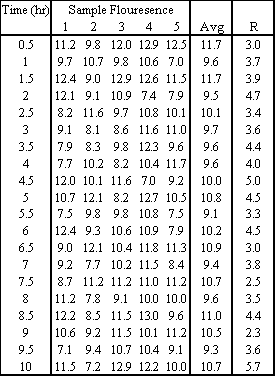
b) El promedio general es 10.2 y el rango promedio es 3.8. Usando el Cuadro 2, A2 = 0.577, D3 = 0 y D4 = 2.114. Por lo tanto:

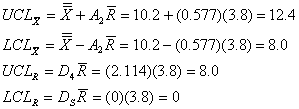
Los gráficos son los siguientes:

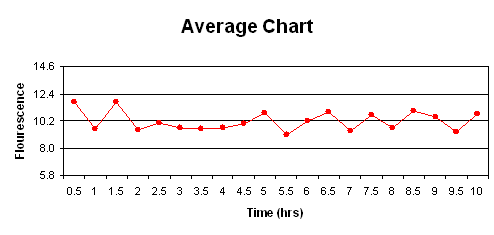
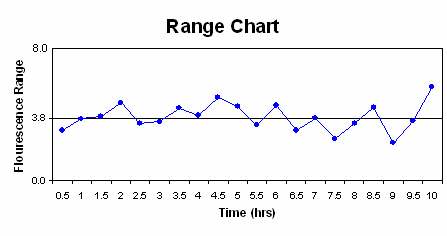
c) No se viola la primera regla ya que ninguno de los puntos queda fuera de los límites de control superior e inferior. Siete o más puntos no caen en un lado de la línea central (el máximo fue de seis), por lo que no se viola la regla dos. No se violó la regla tres, ya que 10 de 11 puntos no cayeron del mismo lado de la línea central (en ouir caso, ocho fue el mx). Por último, no se violó la regla cuatro ya que ninguno de los puntos estaba más cerca de los límites de control que a la línea central. Por lo tanto, este proceso se encuentra bajo control estadístico ya que no se violó ninguna de las reglas.

Ejercicio\(\PageIndex{1}\)

Nuestro muestreador de números aleatorios fue diseñado en base a qué principio clave:

1. Los puntos de datos obtenidos tomando el promedio de varios números aleatorios tienen más probabilidades de ajustarse a una distribución gaussiana.
2. El área bajo una distribución gaussiana siempre está entre cero y uno e igual al valor 'y' de la CDF.
3. La distribución de puntos de datos en una distribución gaussiana es causada por incertidumbres aleatorias.
4. Un proceso bajo control estadístico gaussiano no tendrá una muestra de datos que exceda el límite de control superior o inferior

Responder

A

Ejercicio\(\PageIndex{2}\)

Cuál de las siguientes disminuiría el valor p si se comparan dos conjuntos de datos diferentes:

1. Tamaño de muestra más pequeño
2. Recuento más pequeño de números aleatorios promediados
3. Desviación estándar más pequeña
4. Menor diferencia en los valores medios

Responder

C

Referencias

• Box, George E., William G. Hunter y J S. Hunter. Estadística para Experimentadores: Una Introducción al Diseño, Análisis de Datos y Construcción de Modelos. Nueva York: John Wiley & Sons. 43-45.
• Liptak, Bela G. “Control y Optimización de Procesos”. Manual para Ingenieros de Instrumentos 4:405-413.
• Wheeler, Donald J. y David S. Chambers. Entendiendo el Control Estadístico de Procesos. 2a ed. Knoxville: SPC P. 37-88.
• Woolf, Peter, Amy Keating, Christopher Burge y Michael Yaffe. Estadística e Imprimación de Probabilidad para Biólogos Computacionales. Instituto Tecnológico de Massachusetts. 2004.