13.13: Correlación e información mutua

La aplicación de redes de control a los procesos de ingeniería requiere una comprensión de las relaciones entre las variables del sistema. Uno esperaría, por ejemplo, encontrar una relación entre el caudal de vapor a un intercambiador de calor y la temperatura de la corriente de salida. ¿Cómo, entonces, son los ingenieros para cuantificar el grado de relación entre un par de variables? Muchas veces, las investigaciones sobre la correlación y la información mutua de los conjuntos de datos pueden proporcionar la respuesta. El análisis de correlación proporciona un medio cuantitativo para medir la fuerza de una relación lineal entre dos vectores de datos. La información mutua es esencialmente la medida de cuánto “conocimiento” se puede obtener de una determinada variable al conocer el valor de otra variable. Al utilizar estas técnicas, los ingenieros pueden aumentar la selectividad y precisión de sus sistemas de control.

Correlación

Coeficiente de correlación poblacional

El coeficiente de correlación es una medida importante de la relación entre dos variables aleatorias. Una vez calculado, describe la validez de un ajuste lineal. Para dos variables aleatorias, X e Y, el coeficiente de correlación, ρ _xy, se calcula de la siguiente manera:

\[\rho_{x y}=\frac{\operatorname{cov}(X, Y)}{\sigma_{x} \sigma_{y}} \nonumber \]

Es decir, la covarianza de las dos variables dividida por el producto de sus desviaciones estándar. La covarianza sirve para medir cuánto varían juntas las dos variables aleatorias. Este será un número positivo si ambas variables se encuentran consistentemente por encima del valor esperado y serán negativas si una tiende a estar por encima del valor anticipado y la otra tiende a estar por debajo. Para una descripción más detallada de la covarianza, así como de cómo calcular este valor, consulte Covarianza en Wikipedia.

El coeficiente de correlación tomará valores de 1 a -1. Los valores de 1 y -1 indican ajustes lineales perfectos crecientes y decrecientes, respectivamente. A medida que el coeficiente de correlación poblacional se aproxima a cero desde cada lado, la fuerza del ajuste lineal disminuye. A continuación se muestran rangos aproximados que representan la fuerza relativa de la correlación. Consulte el artículo Correlación en Wikipedia para obtener información más detallada sobre la teoría de correlación que establece estos rangos. Los rangos también aplican para valores negativos entre 0 y -1.

Correlación

• Pequeño: 0.10 a 0.29
• Mediano: 0.30 a 0.49
• Grande: 0.50 a 1.00

Coeficiente de correlación muestral

Una forma modificada de la expresión para el coeficiente de correlación describe la linealidad de una muestra de datos. Para\(n\) las mediciones de variables\(X\) y\(Y\), el coeficiente de correlación muestral se calcula de la siguiente manera:

\[\rho_{x y}=\frac{\sum\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{(n-1) s_{x} s_{y}} \nonumber \]

donde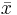 y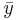 son los promedios de la muestra, y s _{x y s y} son las desviaciones estándar de las muestras. Este coeficiente de correlación seguirá tomando valores de 1 a -1, correspondientes a la fuerza de linealidad de la misma manera que el coeficiente de correlación poblacional. Esta expresión suele ser la más útil para aplicaciones de controles de procesos; un ingeniero puede medir dos variables, calcular sus medias y desviaciones estándar, y finalmente determinar la validez de una relación lineal entre las dos. Este método es extremadamente útil cuando se aplica a una muestra de datos experimentales que pueden ser modelados por una función de distribución normal. Es más simple y más fácil de usar en comparación con el coeficiente de correlación poblacional porque utiliza solo entradas estadísticas bien definidas, media y desviación estándar, en lugar de la función de covarianza compleja.

Supuestos de Coeficiente de Correlación: Linealidad, Distribución Normal

El coeficiente de correlación indica la fuerza de una relación lineal entre dos variables con distribución aleatoria; este valor por sí solo puede no ser suficiente para evaluar un sistema donde estos supuestos no son válidos.

La siguiente imagen muestra diagramas de dispersión del cuarteto de Anscombe, un conjunto de cuatro pares diferentes de variables creados por Francis Anscombe. Las cuatro variables y tienen la misma media (7.5), desviación estándar (4.12), coeficiente de correlación (0.81) y línea de regresión (y = 3 + 0.5x).

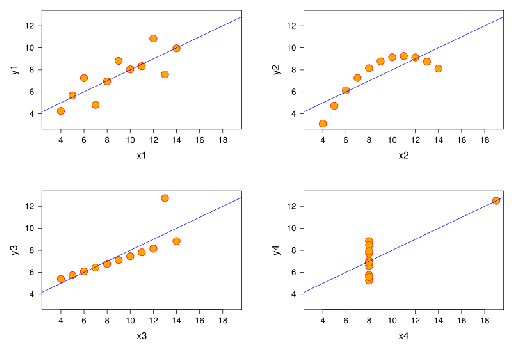
[Imagen de es.wikipedia.org/wiki/Correlación de correlación]

Sin embargo, como se puede observar en las parcelas, la distribución de las variables es muy diferente.

• La gráfica de dispersión de y1 (arriba a la izquierda) parece exhibir distribución aleatoria. Corresponde a lo que se esperaría al considerar dos variables linealmente correlacionadas y siguiendo la distribución normal.
• La gráfica de dispersión de y2 (arriba a la derecha) no presenta distribución aleatoria; una gráfica de sus residuos no mostraría distribución aleatoria. Sin embargo, se puede observar una relación no lineal obvia entre las dos variables.
• La gráfica de dispersión de y3 (abajo a la izquierda) parece exhibir una relación lineal casi perfecta con la excepción de un valor atípico. Este valor atípico ejerce suficiente influencia para disminuir el coeficiente de correlación de 1 a 0.81. Se debe realizar una prueba Q para determinar si un punto de datos debe ser retenido o rechazado.
• La gráfica de dispersión de y4 (abajo a la derecha) muestra otro ejemplo cuando un valor atípico es suficiente para producir un coeficiente de correlación alto, aunque la relación entre las dos variables no sea lineal.

Estos ejemplos indican que el coeficiente de correlación por sí solo no debe utilizarse para indicar la validez de un ajuste lineal.

Aplicaciones de ingeniería

La medición de la correlación de variables del sistema es importante a la hora de seleccionar pares de control manipulados y medidos. Digamos, por ejemplo, que un ingeniero toma varias mediciones de la temperatura y presión dentro de un reactor y señala que los pares de datos tienen un coeficiente de correlación de aproximadamente uno. El ingeniero entiende ahora que al aplicar un sistema de control para mantener la temperatura, también estará controlando la presión del reactor por medio de la relación lineal entre las dos variables.

Aquí comenzamos a ver el papel que juegan las correlaciones en la definición de sistemas MIMO versus SISO. Generalmente, los ingenieros buscan sistemas de control con pares independientes de variables manipuladas (u) y medidas (x). Si dos entradas influyen fuertemente en una sola salida medida por el valor de correlación, entonces el sistema será difícil de desacoplar en un controlador SISO. Valores de correlación más cercanos a 0 para todas las variables manipuladas menos una significa que el sistema será más fácil de desacoplar porque aquí una sola entrada del sistema controla una sola salida del sistema y hay un efecto limitado en otras variables de proceso.

Correlación en Mathematica

Los coeficientes de correlación se pueden calcular rápidamente con la ayuda de Mathematica. Para ilustrar con el ejemplo, supongamos que un ingeniero mide una serie de temperaturas dentro de un quimiostato bacteriano y la concentración de proteína correspondiente en el producto. Mide temperaturas de 298, 309, 320, 333 y 345 K correspondientes a concentraciones de proteína de 0.4, 0.6, 0.7, 0.85 y 0.9 por ciento en peso de proteína (estos valores son para fines ilustrativos y no reflejan el desempeño de un quimiostato real). El ingeniero introduce estas mediciones en Mathematica como un par de vectores de la siguiente manera:

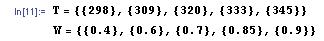
donde T es un vector que contiene las mediciones de temperatura y C es un vector que contiene las mediciones de concentración. Para determinar el coeficiente de correlación, simplemente use la sintaxis a continuación.

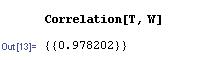
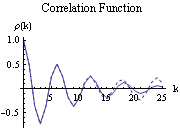
En este caso, el coeficiente de correlación de casi 1 indica un fuerte grado de linealidad entre la temperatura del quimiostato y la concentración de proteína, informando a la ingeniera que esencialmente puede controlar esta concentración a través del control de temperatura. La función de correlación de muestras en Mathematica utiliza una solución aproximada con la media y desviación estándar del conjunto de datos, pero el valor es muy cercano al valor de la función de correlación verdadera. Esto se puede ver en la siguiente figura ya que la línea discontinua representa la función de correlación de muestra, que se desvía ligeramente de la función de correlación verdadera. A medida que la muestra se hace más grande (es decir, mayor n) la aproximación se acerca al valor verdadero. Esto representa una limitación de la función de correlación de muestras y demuestra cómo Mathematica puede usarse para determinar múltiples correlaciones entre conjuntos de datos.

Información Mutua

La información mutua (también conocida como transinformación) es una medida cuantitativa de cuánto nos dice una variable aleatoria (Y) sobre otra variable aleatoria (X). En este caso, la información es pensada como una reducción en la incertidumbre de una variable. Así, cuanta más información mutua entre X e Y, menor incertidumbre hay en X conociendo Y o Y conociendo X. Para nuestros fines, dentro de cualquier proceso dado, se deben seleccionar varios parámetros para poder ejecutar correctamente el proceso. La relación entre variables es integral para determinar correctamente los valores de trabajo para el sistema. Por ejemplo, ajustar la temperatura en un reactor a menudo hace que la presión cambie también. La información mutua se mide más comúnmente en logaritmos de base 2 (bits) pero también se encuentra en base e (nats) y base 10 (bans).

Explicación de Información Mutua

La representación matemática para información mutua de las variables aleatorias A y B son las siguientes:

\[I(A ; B)=\sum_{b \in B} \sum_{a \in A} p(a, b) * \log \left(\frac{p(a, b)}{p(a) p(b)}\right) \nonumber \]

donde,

• \(p(a,b)\)es la función conjunta de distribución de probabilidad de\(A\) y\(B\).
• \(p(a)\)es la función marginal de distribución de probabilidad de\(A\).
• \(p(b)\)es la función marginal de distribución de probabilidad de\(B\).

Para una revisión y discusión de las funciones de distribución de probabilidad, consulte Distribución de probabilidad (Wikipedia).

Al referirse a situaciones continuas, una doble integral reemplaza la doble suma utilizada anteriormente.

\[I(A ; B, c)=\int_{B} \int_{A} p(a, b) * \log \left(\frac{p(a, b)}{p(a) p(b)}\right) d a d b \nonumber \]

donde,

• \(p(a,b)\)es la función conjunta de distribución de probabilidad de\(A\) y\(B\).
• \(p(a)\)es la función marginal de distribución de probabilidad de\(A\).
• \(p(b)\)es la función marginal de distribución de probabilidad de\(B\).

Para una revisión y discusión de las funciones de densidad de probabilidad, consulte Función de densidad de probabilidad (Wikipedia).

Al realizar las funciones anteriores, se mide la distancia entre las funciones de distribución/densidad conjunta de A y B. Dado que la información mutua siempre está midiendo una distancia, el valor obtenido de este cálculo siempre será no negativo y simétrico. Por lo tanto,

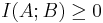
En ambos casos, se está midiendo la información compartida entre A y B. Si A y B son independientes entre sí, entonces la diferencia entre los dos sería cero. En términos de procesos de ingeniería química, dos variables independientes no compartirían información mutua, lo que significa que una variable no proporciona información sobre la otra. Si A y B fueran idénticos, entonces toda la información derivada de la obtención de la variable A proporcionaría los conocimientos necesarios para obtener la variable B.

Al conocer la información mutua entre dos variables A y B, se puede lograr el modelado de un sistema multivariable. Si dos o más variables proporcionan la misma información o tienen efectos similares en un resultado, entonces esto se puede tomar en consideración al construir un modelo. Por ejemplo, si se observaba que el nivel de un tanque era demasiado alto, la presión y la temperatura podrían ser variables plausibles. Si la manipulación de ambas variables provoca un cambio en el nivel de fluido en el tanque, entonces existe alguna información mutua entre la presión y la temperatura. Entonces sería importante establecer la relación entre temperatura y presión para controlar adecuadamente el nivel de fluido en el tanque.

Representación Visual de la Información Mutua

Figura 1. Esta figura demuestra cómo y proporciona información para x. El azul es p (x) y el rojo es\(p(x|y)\) para una y específica. A. y comparte información mutua con x de tal manera que dado a y1 los valores de x ahora se reducen a los cinco valores. B. y comparte información mutua con x pero comparte menos información que A y por lo tanto no es tan útil como A, ya que no elimina tantos valores potenciales de x. C. y no comparte ninguna información mutua. Dado el valor y3, no se eliminan valores x como valores potenciales. Dado que y3 no proporciona ninguna información, no hay información entre las dos variables. D. y comparte información mutua con x. Debido a la distribución bimodal, se requiere un dato más para describir qué distribución se encuentra dentro. Por lo tanto, D da tanta información como la parte B. B da 11 valores potenciales mientras que D da 10 valores potenciales. Sin embargo, se requiere un bit adicional de información para describir en cuál de las dos curvas se encuentran los valores x, por lo que hay 11 entradas necesarias.

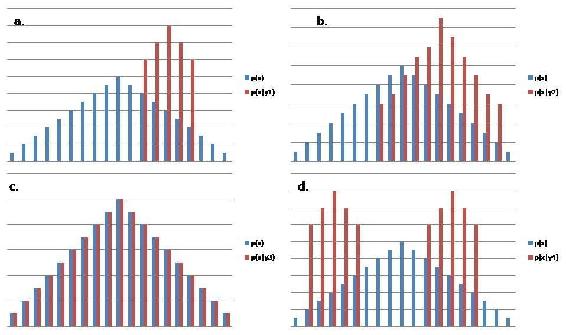
Relacionar la información mutua con otras cantidades/conceptos

La información mutua puede relacionarse con otros conceptos para obtener una comprensión integral de la información obtenida de cualquier parámetro dado. Las discusiones de información mutua se combinan más comúnmente con una discusión sobre la entropía de Shannon (Ver Entropía de Shannon para obtener más información sobre la entropía).

Entropía Relativa

En términos de teoría de probabilidad, la entropía relativa de un sistema mide la distancia entre dos funciones de probabilidad distintas. En aplicaciones de ingeniería química, la información mutua puede ser utilizada para determinar la entropía inherente a un sistema. La información mutua en este aspecto ahora puede definirse simplemente como:

\[I(A ; B)=H(A)-H(A \mid B)=H(B)-H(B A)=I(B ; A)=H(A)+H(B)-H(A, B) \nonumber \]

donde,

• H (A) = entropía marginal de A.
• H (B) = entropía marginal de B.
• H (A | B) = entropía condicional de A.
• H (B | A) = entropía condicional de B.
• H (A, B) = entropía articular de A y B.

Como se describió anteriormente, la entropía marginal todavía representa la incertidumbre alrededor de una variable dada A y B. La entropía condicional describe la incertidumbre en la variable especificada que permanece después de que se conozca la otra variable. En términos de información mutua, las entropías condicionales de A y B nos dicen que es necesario transferir un cierto número de bits desde A para determinar B y viceversa. Una vez más, estos bits de información son determinados por la base logarítmica elegida para el análisis. Se puede determinar la incertidumbre en varios parámetros de proceso diferentes con respecto a cualquier otra variable de proceso.

Información Mutua y Modelos Booleanos

Recordemos que a través de modelos booleanos, una serie compleja de sensores y válvulas se puede modelar en un sistema de control simple. Una variable booleana, sin embargo, nunca devolverá un valor porque solo puede devolver True o False. Este conocimiento se puede combinar para determinar una relación entre dos variables diferentes (a partir del modelo booleano) y luego se puede cuantificar su dependencia (información mutua). Utilizando la misma lógica que se utiliza en la construcción de tablas de verdad, los datos se pueden ingresar en tablas para determinar el valor de información mutua.

Ejemplo de correlación

Supongamos que un ingeniero quiere probar la aplicabilidad de la ley de gas ideal a un tanque cerrado que contiene una cantidad fija del producto gaseoso de su compañía. Dado que el recipiente es de volumen constante, y dado que no ocurrirá ningún cambio en moles en este sistema fijo, se plantearía la hipótesis de que la ley de gas ideal predeciría una relación lineal entre la temperatura y la presión dentro del tanque.

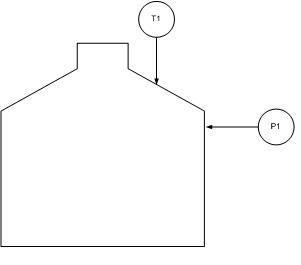
El ingeniero realiza las siguientes medidas y anota sus hallazgos en Excel.

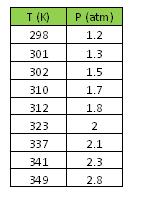
Antes de continuar con su análisis, el ingeniero decide calcular el coeficiente de correlación para estos valores en Mathematica.

Observando el valor aproximado del coeficiente de correlación de 1, el ingeniero procede creando un ajuste lineal de los datos en Excel.

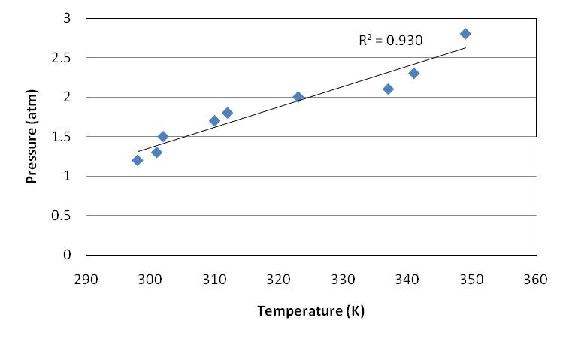
En efecto, los datos son casi lineales.

Resumen

Si un ingeniero intentara determinar si dos variables aleatorias están linealmente relacionadas, calcular los coeficientes de correlación sería el primer paso para determinarlo. Si la media y la desviación estándar para ambas variables son valores conocidos (es decir, calculados a partir de miles de mediciones), entonces se debe utilizar el coeficiente de correlación poblacional. Para determinar el coeficiente de correlación para un conjunto menor de datos, se deben utilizar las ecuaciones de coeficientes de correlación de la muestra. Si se demostrara que las dos variables tienen un alto grado de correlación, el siguiente paso sería graficar los datos y verificar gráficamente la relación lineal de estos datos. Un coeficiente de correlación alto no significa necesariamente que las dos variables estén linealmente relacionadas como lo muestra el cuarteto de Anscombe, por lo que esta comprobación gráfica es necesaria.

La información mutua ayuda a reducir el rango de la función de densidad de probabilidad (reducción de la incertidumbre) para una variable aleatoria X si se conoce la variable Y. El valor de I (X; Y) es relativo, y cuanto mayor es su valor, más información se conoce de X. Generalmente es beneficioso tratar de maximizar el valor de I (X; Y), minimizando así la incertidumbre. El concepto de información mutua es bastante complejo y es la base de la teoría de la información.

Referencias

• Larsen, Richard J. y Marx, Morris L. (2006) Una introducción a la estadística matemática y sus aplicaciones, Nueva Jersey: Prentice Hall. ISBN 0-13-186793-8
• Correlación de Wikipedia.
• Wikipedia Información Mutua.
• Becaria Información Mutua.
• Kojadinovic, Ivan (sin fecha) “Sobre el uso de la información mutua en el análisis de datos: una visión general”