3.1: Invariantes

Utilizamos la simetría y la conservación siempre que encontramos una cantidad que, a pesar de la complejidad circundante, no cambia. Esta cantidad conservada se denomina invariante. Encontrar invariantes simplifica muchos problemas.

Nuestra primera invariante apareció sin previo aviso en la Sección 1.2 cuando estimamos la capacidad de carga de un carril de carretera. La capacidad de carga, la velocidad a la que los autos fluyen por el carril, depende de la separación entre los autos y su velocidad. Podríamos haber intentado estimar cada cantidad y luego la capacidad de carga. Sin embargo, la separación entre los autos y las velocidades de los autos varían mucho, por lo que estas estimaciones son difíciles de hacer de manera confiable.

En cambio, invocamos la regla siguiente de 2 segundos. Mientras los conductores lo obedezcan, la separación entre autos equivale a 2 segundos de manejo. Por lo tanto, un automóvil fluye cada 2 segundos, que es la capacidad de carga del carril (en autos por vez). Al encontrar una invariante, simplificamos un proceso complejo y cambiante. Cuando hay cambio, ¡busca lo que no cambia! (Esta sabiduría proviene de las estrategias de resolución de problemas de Arthur Engel [12].)

3.1.1 ¿Correr o caminar bajo la lluvia?

Practicaremos con esta herramienta al decidir si correr o caminar bajo la lluvia. Se está vertiendo, tu paraguas está sentado en casa, y el hogar se encuentra a unos cientos de metros de distancia.

Para minimizar lo mojado que te vuelves, ¿deberías correr o caminar?

Respondamos a esta pregunta con tres simplificaciones. Primero, supongamos que no hay viento, por lo que la lluvia está cayendo verticalmente. Segundo, supongamos que la lluvia es constante. Tercero, suponga que eres una lámina delgada: Tienes espesor cero a lo largo de la dirección hacia tu casa (esta aproximación fue más válida en mi juventud). Equivalentemente, tu cabeza está protegida por una gorra impermeable, por lo que no te importa si las gotas de lluvia golpean tu cabeza. Intentas minimizar solo la cantidad de agua que golpea tu frente.

Tu único grado de libertad, el único parámetro que puedes elegir, es tu velocidad. Una alta velocidad te deja bajo la lluvia por menos tiempo. Sin embargo, también hace que la lluvia te llegue más directamente (más horizontalmente). Pero lo que permanece constante, independiente de tu velocidad, es el volumen de aire que barres. Debido a que la lluvia es constante, ese volumen contiene un número fijo de gotas de lluvia, independientemente de tu velocidad. Sólo estas gotas de lluvia golpean tu frente. Por lo tanto, te mojas igualmente, sin importar tu velocidad.

Esta sorprendente conclusión es otra aplicación del principio de que cuando hay cambio, buscar lo que no cambia. Aquí, podríamos cambiar nuestra velocidad eligiendo caminar o correr. Sin embargo, no importa cuál sea nuestra velocidad, barremos el mismo volumen de aire, nuestro invariante.

Porque la conclusión de este análisis de invarianza, que no importa si caminas o corres, es sorprendente, es posible que aún albergues una duda persistente. Seguramente correr bajo la lluvia, lo que hacemos casi como reflejo, brinda alguna ventaja sobre un paseo pausado.

¿Es irracional correr para evitar mojarse?

Si eres infinitamente delgado, y solo eres un rectángulo que se mueve bajo la lluvia, entonces se aplica el análisis anterior: Ya sea que corras o camines, tu frente absorberá la misma cantidad de gotas de lluvia. Pero la mayoría de nosotros tenemos un grosor, y el número de gotas que aterrizan sobre nuestra cabeza depende de nuestra velocidad. Si tu cabeza está expuesta y te importa cuántas gotas caen sobre tu cabeza, entonces deberías correr. Pero si tu cabeza está cubierta, siéntete libre de ahorrar energía y disfrutar del paseo. Correr no te mantendrá ninguna secadora.

3.1.2 Endosado de un tablero de ajedrez comido por el ratón

A menudo, una buena manera de practicar una nueva herramienta es en un problema matemático. Entonces no agregamos la complejidad del mundo físico al problema de aprender una nueva herramienta. Aquí, por lo tanto, hay un problema matemático: un juego de solitario.

Un ratón viene y se come dos esquinas diagonalmente opuestas de un tablero de ajedrez estándar de 8 × 8. Tenemos una caja de dominó rectangular, 2×1.

¿Pueden estos dominós tejar el tablero de ajedrez comido por el ratón? En otras palabras, ¿podemos colocar las fichas de dominó para cubrir cada cuadrado exactamente una vez (sin cuadrados vacíos y sin dominó superpuestos)?

Colocar un dominó en el tablero es un movimiento en este juego de solitario. Para cada mudanza, eliges dónde colocar el dominó, así que tienes muchas opciones en cada mudanza. El número de posibles secuencias de movimiento crece rápidamente. En lugar de examinar todas estas secuencias, buscaremos una invariante: una cantidad inalterada por cualquier movimiento del juego.

Debido a que cada dominó cubre un cuadrado blanco y un cuadrado negro, la siguiente cantidad I es invariante (permanece fija):

\[I = \textrm{uncovered black squares} - \textrm{uncovered white squares}\]

En un tablero de ajedrez regular, con 32 cuadrados blancos y 32 cuadrados negros, la posición inicial tiene I = 0. El tablero mordisqueado tiene dos cuadrados negros menos, así que empiezo en 30 − 32 = −2. En la posición ganadora, todas las casillas están cubiertas, por lo que I = 0. Porque yo es invariante, no podemos ganar: Los dominó no pueden poner en mosaico el tablero mordisqueado.

Cada movimiento en este juego cambia el tablero de ajedrez. Al encontrar lo que no cambia, una invariante, simplificamos el análisis.

Los invariantes son poderosos en parte porque son abstracciones. Los detalles de los cuadrados vacíos, sus ubicaciones exactas, se encuentran debajo de la barrera de abstracción. Por encima de la barrera, solo vemos el exceso de cuadrados negros sobre blancos. La abstracción contiene toda la información que necesitamos para saber que nunca podremos tejear el tablero de ajedrez.

Ejercicio\(\PageIndex{1}\): Cube Solitaire

Un cubo tiene números en cada vértice; todos los vértices comienzan en 0 excepto la esquina inferior izquierda, que comienza en 1. Los movimientos son todos de la misma forma: Escoge cualquier borde e incrementa sus dos vértices en uno. El objetivo de este juego de solitario es hacer que todos los vértices sean múltiplos de 3.

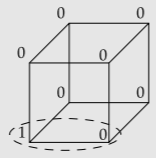
Por ejemplo, al seleccionar el borde inferior de la cara frontal y luego el borde inferior de la cara posterior, se realiza la siguiente secuencia de configuraciones de cubo:

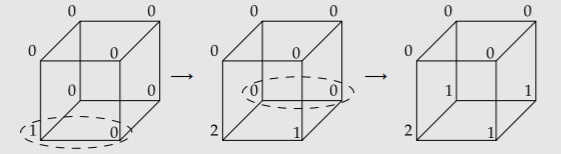
Aunque ninguna configuración anterior gana el juego, ¿puedes ganar con una secuencia de movimientos diferente? Si puedes ganar, da una secuencia ganadora. Si no puedes ganar, prueba que no puedes.

Pista: Crea versiones análogas pero más simples de este juego.

Ejercicio\(\PageIndex{2}\): Triplet solitaire

Aquí hay otro juego de solitario. Comienza con el triplete (3, 4, 5). En cada jugada, elige dos cualquiera de los tres números. Llame a las opciones a y b. Después realice los siguientes reemplazos:

\(a \rightarrow 0.8a - 0.6b\);

\(b \rightarrow 0.6a + 0.8b\).

¿Se puede llegar a (4, 4, 4)? Si puedes, da una secuencia de movimiento; de lo contrario, prueba que es imposible.

Ejercicio\(\PageIndex{3}\): Triplet-solitaire moves as rotations in space

En cada paso del solitario triplete (Problema\(\PageIndex{2}\)), hay tres movimientos posibles, dependiendo de qué par de números de entre a, b y c elijas reemplazar. Describir cada uno de los tres movimientos como una rotación en el espacio. Es decir, para cada movimiento, dar el eje de rotación y el ángulo de rotación.

Ejercicio\(\PageIndex{4}\): Conical pendulum

Encontrar el periodo de un péndulo, incluso a pequeñas amplitudes, requiere cálculo debido a la velocidad variable del péndulo. Cuando haya cambio, busque lo que no cambia. En consecuencia, Christiaan Huygens (1629—1695), llamado “el relojero más ingenioso de todos los tiempos” [20, p. 79] por el gran físico Arnold Sommerfeld, analizó el movimiento de un péndulo que se mueve en un círculo horizontal (un péndulo cónico). Proyectar su movimiento bidimensional sobre una pantalla vertical produce un movimiento de péndulo unidimensional; así, ¡el período del movimiento bidimensional es el mismo que el período del movimiento del péndulo unidimensional! Usa esa idea para encontrar el periodo de un péndulo (¡sin cálculo!).

3.1.3 Escalas logarítmicas

En el juego de solitario de la Sección 3.1.2, una jugada cubrió dos cuadrados de tablero de ajedrez con un dominó. En el juego de entender el mundo, un movimiento frecuente está cambiando el sistema de unidades. Al igual que en el solitario, pregunta: “Cuando se hace tal movimiento, ¿qué es invariante?” Como ejemplo para cristalizar nuestro pensamiento, aquí están las frecuencias relacionadas con el oído humano. Vamos a graficarlos usando kilohercios (kHz) como unidad. Las frecuencias luego se disponen de la siguiente manera:

extremo bajo de la audición: 20 Hz

piano medio C: 262 Hz

piano C más alto: 4186 Hz

gama alta de audición: 20 kHz

Ahora cambiemos las unidades de kilohercios a hercios (Hz) y mantengamos las etiquetas 0, 10 y 20 en sus posiciones actuales en la página. Este cambio aumenta cada espaciado en un factor de 1000: Los nuevos 20 hercios es donde estaban 20 kilohercios (aproximadamente 4 pulgadas o 10 centímetros a la derecha del origen), y 20 kilohercios, el extremo superior del oído humano, se encuentra a 100 metros a nuestra derecha, mucho más allá de los bordes de la página. Esta nueva escala no es muy útil.

Sin embargo, perdimos la oportunidad de usar un invariante: la relación entre frecuencias. Por ejemplo, la relación entre el extremo superior del oído humano (20 kilohercios) y el C medio (262 hercios) es aproximadamente 80. Si usamos una representación basada en relación en lugar de diferencia absoluta, entonces el espaciado entre frecuencias no cambiaría incluso cuando cambiamos la unidad.

Tenemos tal representación: ¡logaritmos! En una escala logarítmica, una distancia corresponde a una relación más que a una diferencia. Para ver el contraste, coloquemos los números del 1 al 10 en una escala logarítmica.

La brecha física entre 1 y 2 representa no su diferencia sino su relación, es decir, 2. Según mi gobernante, la brecha es de aproximadamente 3.16 centímetros. De manera similar, la brecha física entre 2 y 3 —aproximadamente 1.85 centímetros—representa la relación menor 1.5. En contraste con sus posiciones relativas en una escala lineal, 2 y 3 en una escala logarítmica están más cerca de 1 y 2. En una escala logarítmica, 1 y 2 tienen la misma separación que 2 y 4: Ambos huecos representan una relación de 2 y por lo tanto tienen el mismo tamaño físico (3.16 centímetros).

Ejercicio\(\PageIndex{5}\): Practice with ratio thinking

En una escala logarítmica, ¿cómo se compara la brecha física entre 2 y 8 con la brecha entre 1 y 2? Decide en base a tu comprensión de las proporciones; luego revisa tu razonamiento midiendo ambas brechas.

Ejercicio\(\PageIndex{6}\): More practice with ratio thinking

¿La brecha entre 1 y 10 es menor que dos veces, igual a dos veces o más del doble de la brecha entre 1 y 3? Decide en base a tu comprensión de las proporciones; luego revisa tu razonamiento midiendo ambas brechas.

Ejercicio\(\PageIndex{7}\): Moving along a logarithmic scale

En la escala logarítmica del texto, la brecha entre 2 y 3 es aproximadamente de 1.85 centímetros. ¿Dónde aterrizas si comienzas a las 6 y te mueves 1.85 centímetros hacia la derecha? Decide en base a tu comprensión de las proporciones; luego revisa tu razonamiento usando una regla para encontrar la nueva ubicación.

Ejercicio\(\PageIndex{8}\): Extending the scale to the right

En la escala logarítmica del texto, la brecha entre 1 y 10 es de aproximadamente 10.5 centímetros. Si la escala se extendiera para incluir números hasta 1000, ¿qué tan grande sería la brecha entre 10 y 1000?

Ejercicio\(\PageIndex{9}\): Extending the scale to the left

Si la escala logarítmica se extendiera para incluir números hasta 0.01, ¿qué tan lejos a la izquierda de 1 tendría que colocar 0.04?

En una escala logarítmica, las frecuencias relacionadas con la audición se disponen de la siguiente manera:

Cambiar las unidades a kilohercios solo desplaza todas las frecuencias, pero deja sus posiciones relativas invariantes:

Ejercicio\(\PageIndex{10}\): Acoustic energy fluxes

En acústica, la intensidad del sonido se mide por el flujo de energía, el cual se mide en decibelios (dB) —una representación logarítmica de vatios por metro cuadrado. En la escala de decibelios, 0 decibelios corresponde al nivel de referencia de 10 ⁻¹² vatios por metro cuadrado. Cada 10 decibelios (o 1 bel) representa un aumento en el flujo de energía de un factor de 10 (así, 20 decibelios representa un aumento de factor de 100 en el flujo de energía).

a. ¿Cuántos vatios por metro cuadrado son 60 decibelios (el nivel sonoro de la conversación normal)?

b. colocar los siguientes flujos de energía en una escala de decibelios: 10−9 vatios por metro cuadrado (una iglesia vacía), 10−2 vatios por metro cuadrado (primera fila en un concierto de orquesta) y 1 vatio por metro cuadrado (dolorosamente fuerte).

Las escalas logarítmicas ofrecen dos beneficios. Primero, como vimos explícitamente, las escalas logarítmicas incorporan invarianza. El segundo beneficio solo estuvo implícito en la discusión anterior: Las escalas logarítmicas, a diferencia de las escalas lineales, nos permiten representar un amplio rango. Por ejemplo, si incluimos zumbido de línea eléctrica (50 o 60 hercios) en la escala de frecuencia lineal en la p. 61, difícilmente podemos distinguir su posición de 0 kilohercios. La escala logarítmica no tiene ningún problema.

En nuestro mundo caído, los beneficios suelen entrar en conflicto. Uno suele tener que sacrificar un beneficio por otro (velocidad para la precisión o justicia por misericordia). Con escalas logarítmicas, sin embargo, podemos comernos nuestro pastel y tenerlo.

Ejercicio\(\PageIndex{11}\)

Etiquetado de una escala logarítmica

Hagamos una escala para representar tamaños en el universo, desde protones (10−15 metros) hasta galaxias (1030 metros), con personas y bacterias en el medio. Con un rango tan grande, deberíamos usar una escala logarítmica para el tamaño L. ¿Cuál de estas dos formas de etiquetar la báscula es la correcta, y cuál es una tontería?

Las escalas logarítmicas pueden hacer intuitivos los cálculos simbólicos oscuros. Un ejemplo es la media geométrica, que utilizamos en la Sección 1.6 para hacer estimaciones intestinales:

\[estimate = \sqrt{lower \: bound \times upper \: bound}\]

Los medios geométricos también ocurren en el mundo físico. Como encontraste en el Problema 2.9, la distancia d al horizonte, vista desde una altura h sobre la superficie de la Tierra, es

\[d \approx \sqrt{hD}\]

donde\(D = 2R_{Earth}\) está el diámetro de la Tierra. Imagínese a un socorrista sentado con los ojos a una altura h = 4 metros sobre el nivel del mar. Entonces la distancia al horizonte es

\[d \approx (\underbrace{4m}_{h} \times \underbrace{120000 km}_{D})^{1/2}.\]

Para hacer el cálculo, convertimos 12,000 kilómetros a 1.2 × 10 ⁷ metros, calculamos 4 × 1.2×10 ⁷, y calculamos la raíz cuadrada:

\[d \approx \sqrt{4 \times 1.2 \times 10^{7}} m \approx 7000m = 7km\]

En esta forma simbólica con raíz cuadrada, el cálculo oscurece la estructura fundamental de la media geométrica. Primero calculamos hD, que es un área (y muchas veces contiene, como lo hizo aquí, un número enorme). Después tomamos la raíz cuadrada para volver una distancia. No obstante, la zona no tiene nada que ver con la estructura del problema. Se trata simplemente de un dispositivo de contabilidad.

Los dispositivos de contabilidad son útiles; son la forma en que le dices a una computadora qué calcular. Sin embargo, para entender el cálculo, nosotros, como humanos, debemos usar una escala logarítmica para representar las distancias. Esta escala captura la estructura del problema.

¿Cómo podemos describir la posición de la media geométrica\(\sqrt{hD}\)?

La primera pista es que la media geométrica, porque es una media, porque es una media, se encuentra en algún lugar entre h y D. Esta propiedad no es obvia a partir del cálculo utilizando la raíz cuadrada. Para encontrar dónde se encuentra la media geométrica, tenga en cuenta las brechas. En una escala logarítmica, una brecha representa la relación de sus puntos finales. Como se muestra en la tabla, los huecos izquierdo y derecho. En una escala logarítmica, una brecha representa la relación de sus puntos finales. Como se muestra en la tabla, las brechas izquierda y derecha representan la misma proporción,\(\sqrt{D/h}\) ¡es decir! Por lo tanto, en la escala logarítmica, la media geométrica se encuentra exactamente a mitad de camino entre h y D.

Con base en esta representación de la proporción, podemos reformular el cálculo de la media geométrica en una forma que podamos hacer mentalmente

¿Qué distancia es tan grande en comparación con 4 metros como 12,000 kilómetros se compara con ella?

Por falta de imaginación, mi primera conjetura es de 1 kilómetro. Es 12,000 veces menor que el diámetro D (que es 12,000 kilómetros), pero sólo 250 veces mayor que la altura h (4 metros). Mi conjetura de 1 kilómetro es, por tanto, algo demasiado pequeña.

¿Cómo es una conjetura de 10 kilómetros?

Es 2500 veces más grande que h, pero solo 1200 veces menor que D. Me sobrepasé ligeramente. ¿Qué tal 7 kilómetros? Es aproximadamente 1750 veces más grande que 4 metros, y aproximadamente 1700 veces menor que 12 000 kilómetros. Esas brechas están cercanas entre sí, por lo que 7 kilómetros es la media geométrica aproximada.

Del mismo modo, cuando hacemos estimaciones intestinales, debemos colocar nuestras estimaciones inferiores y superiores en una escala logarítmica. Nuestra mejor estimación intestinal es entonces su punto medio. ¡Qué imagen tan simple!

¿Deben colocarse todas las cantidades en una escala logarítmica?

No. Un contraste ilustrativo es entre el tamaño y la posición. Ambas cantidades tienen las mismas unidades. Pero el tamaño varía de 0 a ∞, mientras que la posición varía de −∞ a ∞. Por lo tanto, la posición no se puede colocar en una escala logarítmica (¿dónde pondrías −1 metro?). En contraste, el tamaño (una magnitud) pertenece a una escala logarítmica. En general, los parámetros de ubicación, como la posición, no deben colocarse en una escala logarítmica sino que las magnitudes deberían.