3.2: Controladores dinámicos de primer orden

Controladores de bucle dinámico

Un controlador dinámico\(K(s)\), en el bucle de retroalimentación es un sistema dinámico que condiciona adecuadamente la señal de error\(u(s)=K(s)e(s)\) para afectar la respuesta del sistema de bucle cerrado. La configuración del sistema de control de retroalimentación se muestra a continuación donde\(H(s)=1\) se asume.

Figura\(\PageIndex{1}\): Sistema de control de retroalimentación con planta\(G(s)\), sensor\(H(s)\), y controlador,\(K(s)\).

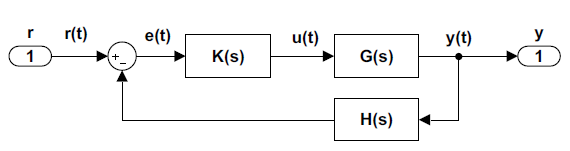
Para analizar el sistema de control de retroalimentación, supongamos que la planta es descrita por\(G\left(s\right)=\frac{n\left(s\right)}{d\left(s\right)}\), y el controlador dinámico es descrito por\(K\left(s\right)=\frac{n_c\left(s\right)}{d_c\left(s\right)}\); entonces, la función de transferencia de bucle cerrado desde la entrada de referencia a la salida de la planta se da como:

\[\frac{y\left(s\right)}{r\left(s\right)}=\frac{n\left(s\right)n_c\left(s\right)}{d\left(s\right)d_c\left(s\right)+n\left(s\right)n_c\left(s\right)}.\]

La función de transferencia de errores de la entrada de referencia a la salida del comparador se da como:

\[\frac{e\left(s\right)}{r\left(s\right)}=\frac{1}{d\left(s\right)d_c\left(s\right)+n\left(s\right)n_c\left(s\right)}.\]

El polinomio característico de bucle cerrado se da como:\(\mathit{\Delta}\left(s\right)= d\left(s\right)d_c\left(s\right)+n\left(s\right)n_c\left(s\right)\).

Controladores dinámicos de primer orden

En particular, consideramos un controlador dinámico de primer orden, descrito por la función de transferencia:

\[K\left(s\right)=K\left(\frac{s+z_c}{s+p_c}\right)\]

El controlador de primer orden agrega un cero ubicado en\(-z_c\) y un polo ubicado en\(-p_c\) a la función de transferencia de bucle:\(KGH(s)\).

Dejar\(G(s)=\frac{n(s)}{d(s)}, \; H(s)=1\); entonces, el polinomio característico de bucle cerrado con el controlador en el bucle se da como:\(\Delta(s)=d(s)(s+p_c)+n(s)(s+z_c)\).

Tradicionalmente, los controladores de primer orden se caracterizan por ser de tipo de fase o de fase de retardo, donde los términos de plomo y retraso se refieren a la contribución de fase del controlador a la gráfica de fase Bode de la función de transferencia de bucle.

Dejar\(K\left(j\omega\right)=K\left(\frac{j\omega+z_c}{j\omega+p_c}\right)\); entonces, la contribución del ángulo de fase del controlador hacia la función de transferencia de bucle se da como:

\[\angle K(j\omega )=\angle (j\omega+z_c)-\angle (j\omega+p_c)={\theta }_z-{\theta }_p\]

donde\({\theta }_z\) y\({\theta }_p\) denotan los ángulos subtendidos por el polo del controlador y cero en una ubicación deseada del polo de bucle cerrado en el plano complejo.

La contribución de fase es positiva para el controlador de fase y negativa para el controlador de retardo de fase (véanse las Figuras 3.2.2 y 3.2.3 a continuación).

Controlador de cable de fase

Un controlador de cable de fase se caracteriza por\(z_{c} <p_{c}\), y contribuye una fase positiva neta a la función de transferencia de bucle.

Ejemplo\(\PageIndex{1}\)

Un controlador de cable de fase se expresa como:\(K\left(s\right)=\frac{s+1}{s+10}\). A continuación se muestra la contribución de fase del controlador.

Figura\(\PageIndex{2}\): Contribución de fase desde un controlador de fase de primer orden.

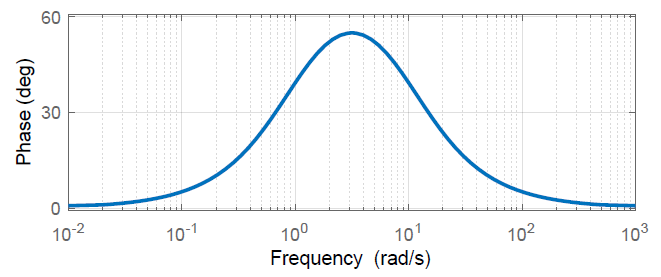
Controlador de retardo de fase

Un controlador de retardo de fase se caracteriza por\(z_{c} >p_{c}\), y contribuye una fase negativa neta a la función de transferencia de bucle.

Ejemplo\(\PageIndex{2}\)

Un controlador de cable de fase se expresa como:\(K\left(s\right)=\frac{s+0.1}{s+0.01}\). A continuación se muestra la contribución de fase del controlador.

Figura\(\PageIndex{3}\): Contribución de fase de un controlador de retardo de fase de primer orden.

Controlador de Lead-Lag

Un controlador de retardo de plomo es un controlador de segundo orden que combina una sección de avance de fase con una sección de retardo de fase; por lo tanto, tiene la forma:

\[K(s)=\frac{K(s+z_{1} )(s+z_{2} )}{(s+p_{1} )(s+p_{2} )} \]

Como ejemplo, se da un controlador de lead-lag como:\(K(s)=\frac{K(s+0.1)(s+10)}{(s+1)^{2} } \).

Podemos observar que el retardo de fase cero se coloca a una frecuencia mucho más baja que la frecuencia del polo dominante, mientras que el cero de fase de avance se coloca cerca de la frecuencia del polo dominante.

Ejemplo de diseño de controlador

La selección de ganancia del controlador para un diseño de fase de plomo se explora en el siguiente ejemplo.

Ejemplo\(\PageIndex{3}\)

El modelo de función de transferencia para un sistema de control de posición se da como:\(G\left(s\right)=\frac{1}{s\left(0.1s+1\right)}\).

Deje que un controlador de fase para el modelo se defina por:\(K\left(s\right)=K\left(\frac{0.1s+1}{0.02s+1}\right)\).

Suponiendo\(H(s)=1\), la función de transferencia de bucle se forma como:\(KG\left(s\right)=\frac{K}{s\left(0.0.02s+1\right)}\).

El polinomio característico de bucle cerrado se formula como:\(\mathit{\Delta}\left(s,K\right)=s(0.02s+1)+K\).

Dejar que se dé un polinomio característico deseado como:\({\mathit{\Delta}}_{des}\left(s\right)=0.02(s^2+50s+1000)\).

Al comparar los coeficientes, obtenemos la ganancia del controlador como:\(K=20\).

De ahí que el controlador dinámico para el sistema se da como:\(K\left(s\right)=20\left(\frac{0.1s+1}{0.02s+1}\right)\).

Podemos notar que al diseñar controladores en cascada, no todas las ubicaciones de polos de bucle cerrado son accesibles. Las ubicaciones de los polos alcanzables se pueden encontrar mediante la aplicación de la técnica de locus radicular (ver Capítulo 5).