7.7: Diseño de Locus Raíz de Controladores Digitales

Diseño de controlador digital

La técnica del locus raíz (Capítulo 5) emplea la función de transferencia de bucle abierto\(KGH(s)\),, para describir el locus de las raíces del polinomio característico de bucle cerrado:\(\mathit{\Delta}\left(s\right)=1+KGH(s)\), con variación en la ganancia del controlador,\(K\).

El locus de la raíz\(z\) -plano describe de manera similar el locus de las raíces del polinomio característico de pulso de bucle cerrado\(\Delta (z)=1+KG(z)\), ya que la ganancia del controlador\(K\) es variada. Entonces\(K\) se puede seleccionar un valor adecuado de la gráfica RL.

Para garantizar la estabilidad de bucle cerrado, las raíces de bucle cerrado deben estar confinadas dentro del círculo unitario.

En MATLAB Control Systems Toolbox, el comando 'rlocus' se utiliza para trazar los loci raíz\(s\)\(z\) -plane y -plane. A continuación se describe el diseño RL del controlador digital.

Diseño para una relación de amortiguación deseada

Suponiendo que las especificaciones de diseño del controlador incluyen una relación\(\zeta ,\) de amortiguación deseada, de los polos de bucle cerrado, consideramos el diseño del locus raíz\(z\) -plane basado en el\(\zeta\) requisito.

Para una función prototipo de transferencia de segundo orden:\(T(s)=\frac{\omega _{n}^{2} }{s^{2} +2\zeta \omega _{n} s+\omega _{n}^{2} }\), las\(\zeta\) líneas constantes se definen por:\(\frac{\sigma }{\omega } =\mp \frac{\zeta }{\sqrt{1-\zeta ^{2} } }\). \(\zeta\)Las líneas constantes en el plano z se obtienen por:\(z=e^{Ts} =e^{\sigma T} e^{\pm j\omega T}\), donde\(\sigma =\mp \frac{\zeta }{\sqrt{1-\zeta ^{2} } } \omega\) y\(\omega T\) va desde\(0\) hasta\(\pi\).

En MATLAB Control Systems Toolbox, el comando 'grid' muestra las\(\zeta\) líneas constantes en el\(z\) plano complejo. El comando grid muestra además\((\omega _{n} )\) contornos de frecuencia constante que son útiles para seleccionar un tiempo de muestreo adecuado\((T)\) dada la frecuencia natural del modelo. La región deseada en el\(z\) plano para ubicaciones de raíz de bucle cerrado se puede especificar como:\(0.1\pi \le \omega _{n} T\le 0.5\pi ,\; \, \, \zeta \ge 0.6\), que asume una frecuencia de muestreo entre\(2\ and10\) veces la frecuencia natural del sistema analógico.

Ejemplo\(\PageIndex{1}\)

Vamos\(G(s)=\frac{1}{s(s+1)}\),\(T=0.2\rm s\); entonces, tenemos:\(G(z)=\frac{0.0187z+0.0175}{(z-1)(z-0.819)}\). Supongamos que las especificaciones de diseño requieren\(\zeta =0.7\).

El polinomio característico de pulso de bucle cerrado se obtiene como:\(\Delta (z)=z^{2} +(0.0187\, K-1.819)z+0.0175\, K+0.819.\)

El locus raíz\(z\) -plane se traza usando el comando 'rlocus' MATLAB y se muestra en la Fig. 7.7.1. De la gráfica RL del plano z (Figura 7.7.1), podemos elegir, por ejemplo\(K=0.46\), tener\(\zeta =0.7\) para las raíces de bucle cerrado.

Figura\(\PageIndex{1}\): Diseño de locus radicular en el plano z.

El polinomio característico de pulso resultante es:\(\Delta (z)=z^{2} -1.81z+0.827,\) con raíces de bucle cerrado ubicadas en:\(z=0.9\pm j0.09.\) El uso del comando MALTAB 'húmedo' muestra una relación de amortiguación de\(\zeta =0.7\) con una frecuencia natural\(\omega _{n} =0.68\, \, {\rm rad/s}\).

A modo de comparación, el sistema de tiempo continuo tiene un polinomio característico:\(\Delta (s)=s^{2} +s+K,\); para\(K=0.46\), las raíces de bucle cerrado se localizan en\(s=0.5\pm j0.46\) con\(\zeta =0.74\) con\(\omega _{n} =0.68\, \, {\rm rad/s}\).

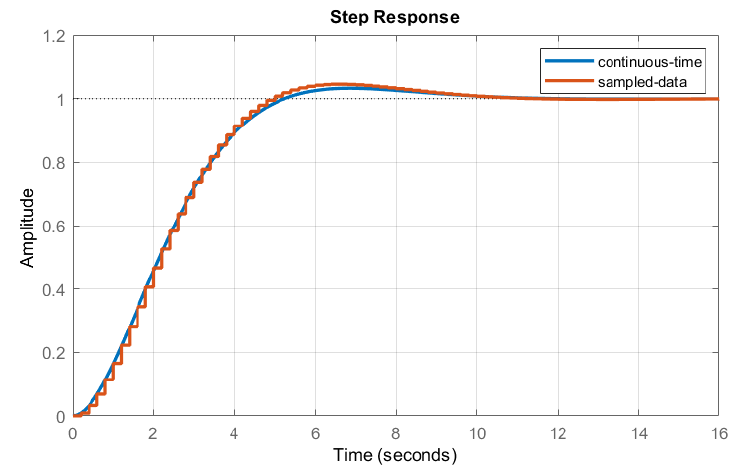
Las respuestas escalonadas de los sistemas analógicos y discretos se comparan en la Figura 7.7.2.

Figura\(\PageIndex{2}\): Respuesta escalonada de los sistemas de tiempo continuo y datos muestreados en bucle cerrado.

Diseño para tiempo de sedimentación y relación de amortiguación

El tiempo de asentamiento y la relación de amortiguación de las raíces dominantes de bucle cerrado en el\(z\) plano se relacionan como:\(re^{\pm j\theta } =e^{-\zeta \omega _{n} T} e^{\pm j\omega _ d T} ,\; \; \omega _ d =\omega _{n} \sqrt{1-\zeta ^{2} } .\)

Al separar en parte real e imaginaria da dos ecuaciones:\(\ln r\; =-\zeta \omega _{n} T\) y\(\theta =\omega _{d} T\), que se pueden resolver para obtener:

\[\zeta =-\ln r/\sqrt{\ln ^{2} r\; +\theta ^{2} }\]

\[\omega _{n} =\sqrt{\ln ^{2} r\; +\theta ^{2} } /T\]

\[\tau =\frac{1}{\zeta \omega _{n} } =-\frac{T}{\ln r\; } .\]

Ejemplo\(\PageIndex{2}\)

Vamos\(G(z)=\frac{0.0187z+0.0175}{(z-1)(z-0.819)}\). El polinomio característico de pulso de bucle cerrado se obtiene como:\(\Delta (z)=z^{2} +(0.0187\, K-1.819)z+0.0175\, K+0.819.\)

Para\(\zeta =0.7\), las raíces de bucle cerrado\(z\) -plano se encuentran en:\(z=0.905\pm j0.0875=0.91\; e^{\pm j0.096}\). Entonces, de las relaciones anteriores, obtenemos:\(\zeta =0.7,\; \omega _{n} =0.74,\; \tau =2.1\; {\rm s,\; }t_\rm s =4.6\, \tau =9.5\, \rm s.\)

Una comparación de controladores analógicos y digitales

El siguiente ejemplo compara el diseño del locus raíz de controladores analógicos y digitales en el caso de un modelo de motor de CC.

Ejemplo\(\PageIndex{3}\)

Un modelo de motor de CC se describe como:\(G\left(s\right)=\frac{500}{s^2+110s+1025}\); las especificaciones de diseño son para que la respuesta de paso del motor tenga:\(OS\le 10\%\ (\zeta \ge 0.59),\ \ t_s\le 100ms,\ \ e{\left(\infty \right)|}_{step}=0.\)

El tiempo de muestreo se selecciona como:\(T=0.01s\); luego, a partir del comando MATLAB 'c2d', se obtiene la función de transferencia de impulsos del motor como:\(\ G\left(z\right)=\frac{0.0178z+0.0123}{z^2-1.27z+0.333}\).

Para obtener un error de estado estacionario cero, podemos elegir un controlador PI, donde el controlador cero cancela aproximadamente un polo de planta, es decir, let\(K\left(s\right)=\frac{K\left(s+10\right)}{s}\).

Se obtiene un controlador PI comparable para el sistema de datos muestreados mediante el uso de la transformación:\(z=e^{Ts}\), y se da como:\(K\left(z\right)=\frac{K\left(z-0.905\right)}{z-1}\).

Las gráficas de locus de raíz\(s\)\(z\) -plano y -plano se muestran en la Figura 7.7.3. De las parcelas, podemos elegir, por ejemplo,\(K=8\) para que el sistema de bucle cerrado logre una constante de tiempo:\(\tau \cong 25ms\).

Figura\(\PageIndex{3}\): Gráfica de locus raíz para el modelo de motor de CC: diseño de sistema analógico (izquierda); diseño de sistema de datos muestreados (derecha).

Para\(K=8\), las funciones de transferencia de bucle cerrado resultantes para sistemas analógicos y discretos se obtienen como:

Analógico:\(T\left(s\right)=\frac{4000\left(s+10\right)}{s^3+110s^2+5025s+40,000}\)

Discreta:\(T\left(z\right)=\frac{0.14z^2-0.03z-0.089}{z^3-2.13z^2+1.57z-0.42}\)

El uso del comando 'húmedo' de MATLAB muestra una amortiguación\(\zeta =0.79\) para el sistema analógico y una amortiguación\(\zeta =0.68\) para el sistema digital.

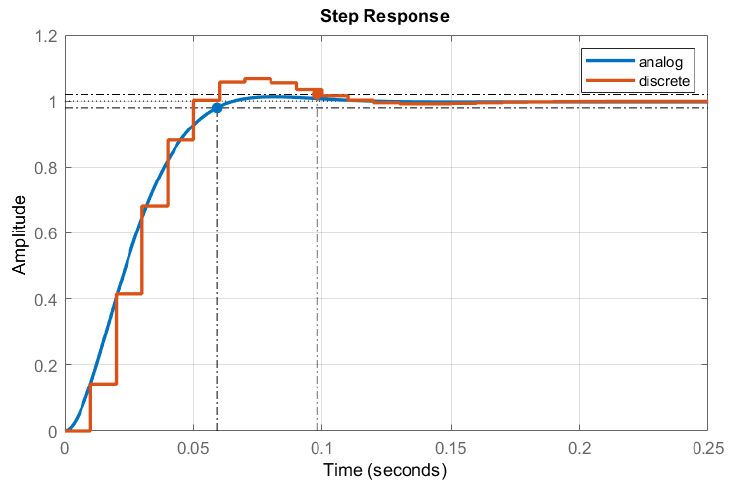
Las respuestas escalonadas de los sistemas analógico y discreto se comparan en la Figura 7.7.4. Como se ve en la figura, tanto los sistemas analógicos como los discretos cumplen con los requisitos de tiempo de asentamiento y sobreimpulso.

Figura\(\PageIndex{4}\): Respuesta escalonada del motor de CC para el diseño del controlador PI analógico y discreto.

Diseño de controlador PID sintonizado MATLAB

MATLAB Control Systems Toolbox proporciona un comando 'pidtune' que se puede utilizar con modelos de sistemas analógicos y discretos. El diseño del controlador PID sintonizado en el caso de un motor de CC se explora en el siguiente ejemplo.

Ejemplo\(\PageIndex{4}\)

Let\(G\left(s\right)=\frac{500}{s^2+110s+1025}\); las especificaciones de diseño son para que la respuesta de paso del motor tenga:\(OS\le 10\%\ (\zeta \ge 0.59),\ \ t_s\le 100ms,\ \ e{\left(\infty \right)|}_{step}=0.\)

Let\(T=0.01s\); del comando MATLAB 'c2d', la función de transferencia de impulsos del motor se obtiene como:\(\ G\left(z\right)=\frac{0.0178z+0.0123}{z^2-1.27z+0.333}\).

Mediante el uso del comando 'pidtune' de MATLAB, se obtiene un controlador PID analógico para el modelo de motor de CC con una frecuencia de\(100rad/s\) cruce de:\(K\left(s\right)=25.1+0.189s+\frac{567}{s}\).

El comando 'pidtune' se utiliza para diseñar un controlador PID similar para el modelo discreto. El resultado es:\(K\left(z\right)=23.4+0.368\left(\frac{z-1}{T}\right)+202\left(\frac{T}{z-1}\right)\).

Las respuestas unit-step de los sistemas de bucle cerrado para los modelos analógicos y discretos se comparan en la Figura 7.7.5. Ambos controladores logran un tiempo de asentamiento\(t_s<0.1s\) sin error de estado estacionario. Sin embargo, en este caso, el controlador PID digital sintonizado tiene un menor tiempo de sedimentación.

Figura\(\PageIndex{5}\): Respuesta escalonada del motor de CC para el diseño del controlador PID analógico y discreto.