10.2: Controladores para modelos de variables de estado discreto

Emulación de un controlador analógico

El controlador de colocación de polos diseñado para un modelo de variable de estado de tiempo continuo se puede usar con un modelo de sistema de datos muestreados derivado. La emulación exitosa del controlador requiere una frecuencia de muestreo lo suficientemente alta que sea al menos diez veces la frecuencia de los polos dominantes de bucle cerrado del sistema.

A continuación ilustramos la emulación del controlador de colocación de polos diseñado para el modelo de motor de CC (Ejemplo 8.3.4) para controlar el modelo de tiempo discreto del motor de CC. El modelo de motor de CC se discretiza a dos frecuencias de muestreo diferentes para su comparación, asumiendo ZOH en la entrada de la planta.

Ejemplo\(\PageIndex{1}\)

Las ecuaciones de estado y salida para un modelo de motor de CC se dan como:

\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]=\left[\begin{array}{cc} {-100} & {-5} \\ {5} & {-10} \end{array}\right]\left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]+\left[\begin{array}{c} {100} \\ {0} \end{array}\right]V_a , \;\;\omega =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right].\]

El modelo de motor se discretiza a dos velocidades de muestreo diferentes en MATLAB. Los resultados son:

\[T=0.01s: A_{\rm d} =\left[\begin{array}{cc} {0.367} & {-0.030} \\ {0.030} & {0.904} \end{array}\right],\; \; B_{\rm d} =\left[\begin{array}{c} {0.632} \\ {0.018} \end{array}\right],\; \; C_{\rm d} =\left[\begin{array}{cc} {0} & {1} \end{array}\right].\]

\[T=0.02s: A_{\rm d} =\left[\begin{array}{cc} {0.134} & {-0.038} \\ {0.038} & {0.816} \end{array}\right],\; \; B_{\rm d} =\left[\begin{array}{c} {0.863} \\ {0.053} \end{array}\right],\; \; C_{\rm d} =\left[\begin{array}{cc} {0} & {1} \end{array}\right].\]

Para un polinomio característico deseado:\(\Delta _{\rm des} (s)=s^{2} +150\,s+5000\), se obtuvo un controlador de retroalimentación de estado para el modelo de variable de estado de tiempo continuo como (Ejemplo 9.1.1):\(k^{T} =\left[\begin{array}{cc} {0.4} & {7.15} \end{array}\right]\).

Podemos usar el mismo controlador para controlar los modelos correspondientes del sistema de datos de muestra.

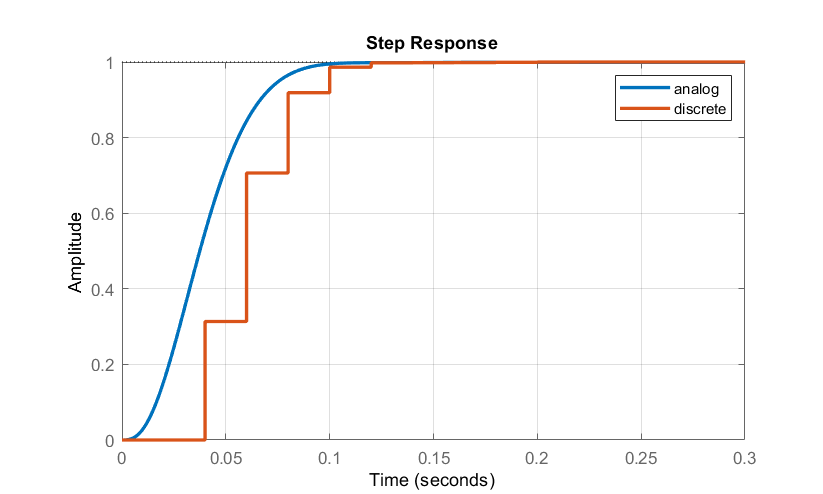
La respuesta unidad-paso del sistema de bucle cerrado se simula en la Figura 10.2.1, donde se trazan ambas variables de estado\(\omega \left(t\right)\),\(i_a\left(t\right)\) y,.

Figura\(\PageIndex{1}\): La respuesta escalonada del modelo de motor de CC con emulación de controlador analógico: corriente de armadura (arriba); velocidad del motor (abajo)

Observamos a partir de la figura que la corriente de la armadura tiene un sobreimpulso mayor a la menor frecuencia de muestreo, aunque ambos modelos muestran un tiempo de asentamiento similar de aproximadamente 100 mseg.

Diseño de colocación de postes de controlador digital

Dado un modelo\(\left\{A_{\rm d},\ B_{\rm d}\right\}\) de variable de estado discreto y un polinomio característico de pulso deseado\(\Delta _{\rm des} (z)\), se puede diseñar un controlador de retroalimentación de estado para el sistema utilizando una colocación de polos similar a la del sistema de tiempo continuo (Sec. 9.1.1).

Que se dé el modelo de tiempo discreto de un sistema SISO como:

\[{\bf x}_{k+1} ={\bf A}_{\rm d} {\bf x}_{k} +{\bf b}_{\rm d} u_{k} , \;\; y_{k} ={\bf c}^T {\bf x}_{k} \]

Un controlador de realimentación de estado para el modelo de variable de estado discreto se define como:

\[u_k=-{\bf k}^T{\bf x}_k+r_k\]

donde\({\bf k}^{T}\) representa un vector de fila de ganancias de retroalimentación constantes y\(r_k\) es una secuencia de entrada de referencia. Las ganancias del controlador se pueden obtener equiparando los coeficientes del polinomio característico con los de un polinomio deseado:

\[\Delta (z)=\left|z{\bf I-A}_{\rm d} \right|=\Delta _{\rm des} (z)\]

Lo\(\Delta _{\rm des} (z)\) anterior es un polinomio Hurwitz (in\(z\)), con raíces dentro del círculo unitario que cumplen con los requisitos de rendimiento (relación de amortiguación y/o tiempo de asentamiento) dados. Suponiendo que se conocen las ubicaciones de raíz del\(s\) plano deseado, las ubicaciones\(z\) de raíz de plano correspondientes se pueden obtener a partir de la equivalencia:\(z=e^{Ts}\).

Sistema de circuito cerrado

El modelo de sistema de bucle cerrado se da como:

\[{\bf x}_{k+1} ={\bf A}_{\rm cl} {\bf x}_{k} +{\bf b}_{\rm d} r_{k} , \;\; y_{k} ={\bf c}^T {\bf x}_{k} \]

donde\({\bf A}_{\rm cl} =({\bf A}_{\rm d}-{\bf b}_{\rm d}{\bf k}^T)\).

Suponiendo estabilidad de bucle cerrado, para una entrada constante\(r_k=r_{\rm ss}\), la respuesta de estado estacionario\({\bf x}_{\rm ss}\),, del sistema obedece:

\[{\bf x}_{ss} ={\bf A}_{\rm cl} {\bf x}_{ss} +{\bf b}_{\rm d} r_{ss} ,\;\; y_{\rm ss} ={\bf c}^T {\bf x}_{ss} \]

De ahí,\(y_{\rm ss}={\bf c}^T\,({\bf A}_{\rm cl}-{\bf I})^{-1}\,{\bf b}_{\rm d}\,r_{\rm ss}\).

Ejemplo\(\PageIndex{2}\)

El modelo de variable de estado discreto de un motor\(T=0.02\) o motores de CC se da como:\[\left[\begin{array}{c} {i_{k+1} } \\ {\omega _{k+1} } \end{array}\right]=\left[\begin{array}{cc} {0.134} & {-0.038} \\ {0.038} & {0.816} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]+\left[\begin{array}{c} {0.863} \\ {0.053} \end{array}\right]V_{k} , \;\; y_{k} =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]\]

Las ubicaciones de raíz\(s\) -plane deseadas para el modelo se dan como:\(s=-50,\; -100.\)

Las raíces\(z\) -plano correspondientes (\(T=0.02s\)) se obtienen como:\(z=e^{-1} ,\; e^{-2}\).

El polinomio característico deseado se da como:\(\Delta _{\rm des} (z)=z^{2} -0.95z+0.05.\)

Las ganancias de retroalimentación\(k^T =[k_{1} ,\; k_{2} ]\), calculadas usando el comando 'place' de MATLAB, se dan como:\(k_{1} =0.247,\; k_{2} =4.435.\)

La matriz del sistema de bucle cerrado se da como:\(A_\rm d)= \left[\begin{array}{cc} {-0.080} & {-3.867} \\ {0.025} & {0.583} \end{array}\right]\).

Se obtiene una regla de actualización para la implementación del controlador en la computadora como:\(u_{k} =-0.247\, i_{k} -4.435\, \omega _{k} .\)

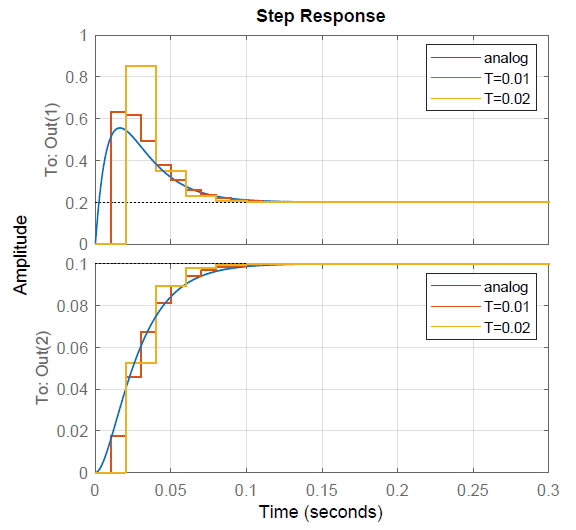
La respuesta de bucle cerrado tiene un valor de estado estacionario de\(\omega _{\rm ss}=0.143 \;\rm rad/s\).

La respuesta escalonada del sistema de bucle cerrado se representa en la Figura 10.2.2, donde la respuesta discreta del sistema se escaló para que coincidiera con la respuesta del sistema analógico. La respuesta escalonada del sistema de tiempo continuo y la de las ganancias del controlador emulado se trazan al lado.

Figura\(\PageIndex{2}\): Respuesta unidad-paso del modelo de motor de CC para las siguientes opciones: sistema analógico; emulación de controlador; controlador digital.

Diseño de controlador Deadbeat

Un sistema de tiempo discreto se llama deadbeat si todos los polos de bucle cerrado se colocan en el origen\((z=0)\).

Un sistema deadbeat tiene la notable propiedad de que su respuesta alcanza el estado estacionario en\(n\) -pasos, donde\(n\) representa la dimensión del modelo.

El polinomio característico de pulso de bucle cerrado deseado se selecciona como\(\Delta _{\rm des} (z)=z^{n}\).

Para diseñar un controlador de ritmo muerto, deje que la función de transferencia de pulsos de bucle cerrado se defina como:\[T(z)=\frac{K(z)G(z)}{1+K(z)G(z)} \]

La ecuación anterior se resuelve\(K(z)\) para obtener:\[K(z)=\frac{1}{G(z)} \frac{T(z)}{1-T(z)} \]

Deje que el deseado\(T(z)=z^{-n}\); entonces, el controlador deadbeat se da como:\[K(z)=\frac{1}{G(z)(z^{n} -1)}\]

Ejemplo\(\PageIndex{3}\)

Vamos\(G(s)=\frac{1}{s+1} ;\) entonces\(G(z)=\frac{1-e^{-T} }{z-e^{-T} }\).

Se obtiene un controlador deadbeat para el modelo como:\(K(z)=\frac{z-e^{-T} }{(1-e^{-T} )(z-1)}\).

Ejemplo\(\PageIndex{4}\)

El modelo de variable de estado discreto de un motor de CC para\(T=0.02\; \rm s\) se da como:\[\left[\begin{array}{c} {i_{k+1} } \\ {\omega _{k+1} } \end{array}\right]=\left[\begin{array}{cc} {0.134} & {-0.038} \\ {0.038} & {0.816} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]+\left[\begin{array}{c} {0.863} \\ {0.053} \end{array}\right]V_{k} , \;\;y_{k} =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]\]

El controlador de retroalimentación de estado se da como:\(u_{k} =-\left[k_{1} ,\, \, k_{2} \right]x_{k}\).

El polinomio característico de bucle cerrado se obtiene como:\[\Delta (z)=z^{2} +(0.863k_{1} +0.053k_{2} -0.95)z-0.707k_{1} +0.026k_{2} +0.111\]

Para el diseño de colocación de postes, deje\(\Delta _{\rm des} (z)=z^{2}\). Al igualar los coeficientes polinomiales, las ganancias del controlador de deadbeat se obtienen como:\(k_{1} =0.501,\; k_{2} =9.702\).

La regla de actualización para la implementación del controlador se da como:\[u_{k} =0.501\, \, i_{k} +9.702\, \, \omega _{k} \]

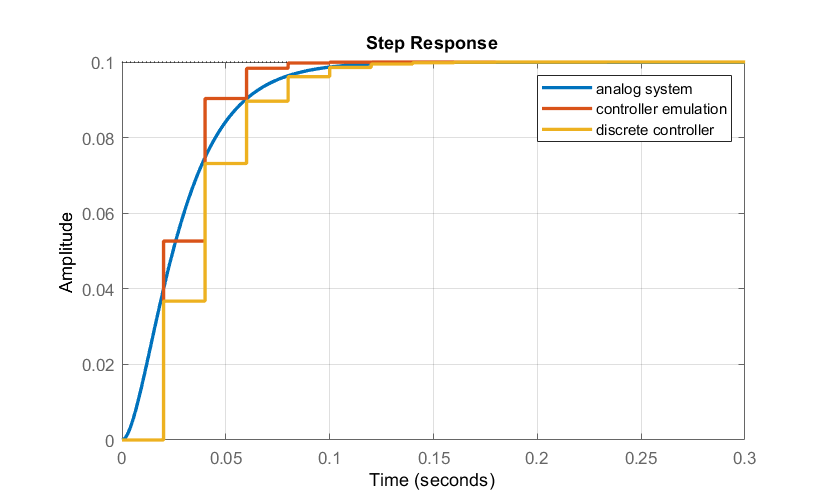
La respuesta escalonada del controlador deadbeat (Figura 10.2.3) se asienta en dos periodos de tiempo. La respuesta se escaló para que coincidiera con la del sistema de tiempo continuo.

Se puede realizar un diseño de punto muerto aproximado eligiendo distintos valores propios de bucle cerrado cerca del origen, por ejemplo\(z=\pm {10}^{-5}\), y usando el comando 'place' de MATLAB Control Systems Toolbox.

Las ganancias de retroalimentación para el diseño aproximado se obtienen como:\(k_{1} =0.509,\; k_{2} =9.702\). La respuesta resultante del sistema de bucle cerrado sigue siendo inactiva.

Figura\(\PageIndex{3}\): La respuesta escalonada del modelo de motor de CC con controlador deadbeat.

Diseño de sistemas de seguimiento Feedforward

Un sistema de seguimiento fue diseñado previamente mediante el uso de cancelación de feedforward de la señal de error (Sección 9.2.1). Un diseño similar se puede realizar en el caso de sistemas discretos.

Hacia este fin, dejemos que el modelo de variable de estado discreto se dé como:\[{\bf x}_{k+1} ={\bf A}_{\rm d} {\bf x}_{k} +{\bf b}_{\rm d} u_{k} , \;\;y_{k} ={\bf c}^T {\bf x}_{k} \]

Un controlador de seguimiento para el modelo se define como:\[u_k=-{\bf k}^T{\bf x}_k+k_rr_k\] donde\({\bf k}^{T}\) representa un vector de fila de ganancias de retroalimentación,\(k_r\) es una ganancia de alimentación directa y\(r_k\) es una secuencia de entrada de referencia.

Suponiendo que se ha diseñado un controlador de colocación de polos para el sistema discreto, el sistema de bucle cerrado se da como:\[{\bf x}_{k+1}=\left({\bf A}_{\rm d}-{\bf b}_{\rm d}{\bf k}^T\right){\bf x}_k+{\bf b}_{\rm d}k_rr_k\]

La función de transferencia de impulsos de bucle cerrado se obtiene como:\[T\left(z\right)={\bf c}^T_{\rm d}{\left(z{\bf I-A}_{\rm d}+{\bf b}_{\rm d}{\bf k}^T\right)}^{-1}{\bf b}_{\rm d}k_r\] donde\({\bf I}\) denota una matriz de identidad. La condición para el seguimiento asintótico se da como:\[T\left(1\right)={\bf c}^T_{\rm d}{\left({\bf I-A}_{\rm d}+{\bf b}_{\rm d}{\bf k}^T\right)}^{-1}{\bf b}_{\rm d}k_r=1\]

La ganancia de feedforward para la cancelación de errores se obtiene como:\(k_r=\frac{1}{T\left(1\right)}\).

Ejemplo\(\PageIndex{5}\)

El modelo de variable de estado discreto de un motor\(T=0.02\) o motores de CC se da como:\[\left[\begin{array}{c} {i_{k+1} } \\ {\omega _{k+1} } \end{array}\right]=\left[\begin{array}{cc} {0.134} & {-0.038} \\ {0.038} & {0.816} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]+\left[\begin{array}{c} {0.863} \\ {0.053} \end{array}\right]V_{k} , \;\;y_{k} =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]\]

Un controlador de retroalimentación de estado para el modelo de motor fue diseñado previamente como:\(k^T =[k_{1} ,\; k_{2} ]\), donde\(k_{1} =0.247,\; k_{2} =4.435.\)

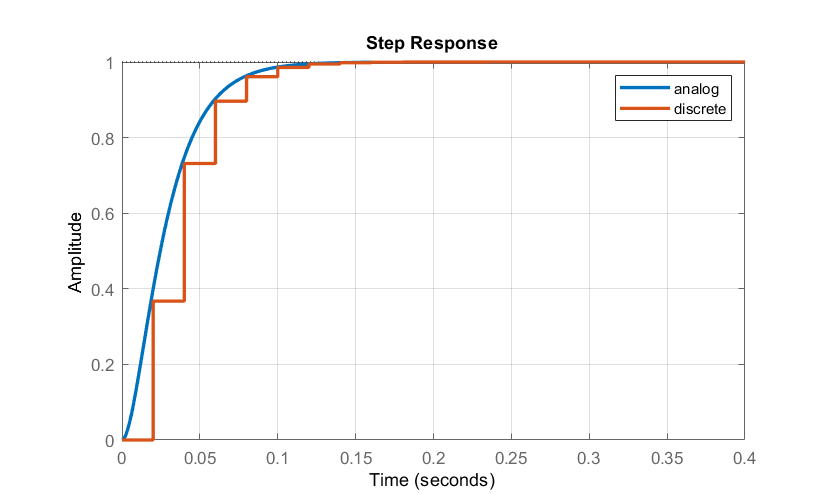
El sistema de bucle cerrado se define como:\[T\left(z\right)=\frac{0.367z+0.179}{z^2-0.503z+0.05}k_r\]

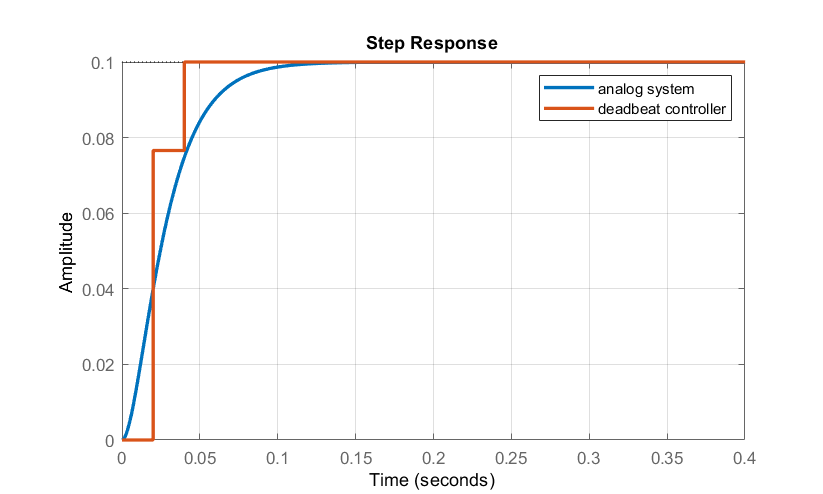
A partir de la condición asintótica, la ganancia feedforward se resuelve como:\(k_r=6.98\).

La respuesta escalonada del sistema de bucle cerrado se muestra en la Figura 10.2.4.

Figura\(\PageIndex{4}\): La respuesta escalonada de los controladores de seguimiento para el modelo de motor de CC.

Ejemplo\(\PageIndex{6}\)

El modelo de variable de estado discreto de un motor\(T=0.02\) o motores de CC se da como:

\[\left[\begin{array}{c} {i_{k+1} } \\ {\omega _{k+1} } \end{array}\right]=\left[\begin{array}{cc} {0.134} & {-0.038} \\ {0.038} & {0.816} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]+\left[\begin{array}{c} {0.863} \\ {0.053} \end{array}\right]V_{k} , \;\;y_{k} =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]\]

Se diseñó un controlador dead-beat para el modelo de motor como:\(k^T =[k_{1} ,\; k_{2} ]\), dónde\(k_{1} =0.501,\; k_{2} =9.702\).

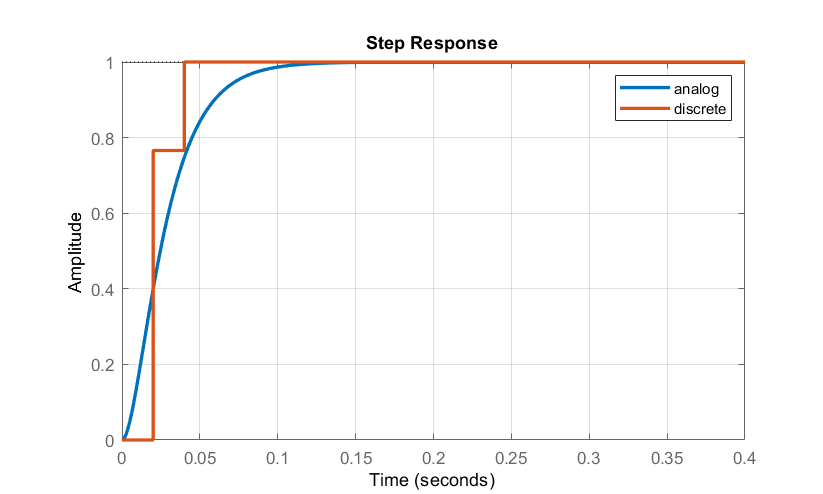
El sistema de bucle cerrado se define como:\[T\left(z\right)=\frac{0.672z+0.328}{z^2}k_r\]

A partir de la condición asintótica, la ganancia feedforward se resuelve como:\(k_r=12.77\).

La respuesta escalonada del sistema de bucle cerrado se muestra en la Figura 10.2.5.

Figura\(\PageIndex{5}\): La respuesta escalonada del controlador de seguimiento de deadbeat para el modelo de motor de CC.

Diseño de controlador PI de seguimiento

Un controlador PI de seguimiento para el modelo de variable de estado discreto está diseñado de manera similar al diseño del sistema de tiempo continuo (Figura 9.3.1). El controlador PI de seguimiento coloca un integrador en el bucle de retroalimentación, asegurando así que el error de seguimiento llegue a cero en el estado estacionario.

En el caso del sistema de tiempo continuo, el controlador PI de seguimiento se definió como:\(u=-{\bf k}^{T} {\bf x}+k_{i} \int (r-y)\rm dt\).

Usando la aproximación de diferencia directa al integrador, dada como:\(v_k=v_{k-1}+Te_k\), un modelo de sistema de tiempo discreto incrementado que incluye la variable de estado del integrador se forma como:

\[\left[\begin{array}{c} {{\bf x}(k+1)} \\ {v(k+1)} \end{array}\right]=\left[\begin{array}{cc} {{\bf A}_{\rm d} } & {\bf 0} \\ {-{\bf c}^T T} & {1} \end{array}\right] \left[\begin{array}{c} {{\bf x}(k)} \\ {v(k)} \end{array}\right]+\left[\begin{array}{c} {{\bf b}_{\rm d} } \\ {0} \end{array}\right]u+\left[\begin{array}{c} {\bf 0} \\ {T} \end{array}\right]r\]

El controlador de retroalimentación de estado para el sistema incrementado se define como:

\[u(k)=\left[\begin{array}{cc} {-{\bf k}^T } & {k_ i } \end{array}\right]\, \left[\begin{array}{c} {{\bf x}(k)} \\ {v(k)} \end{array}\right]\]

donde\(k_ i\) representa la ganancia integral. Con la adición del controlador anterior, el sistema de bucle cerrado se describe como:

\[\left[\begin{array}{c} {{\bf x}(k+1)} \\ {v(k+1)} \end{array}\right]=\left[\begin{array}{cc} {{\bf A}_{\rm d} -{\bf b}_{\rm d} k^{T} } & {{\bf b}_{\rm d} k_{i} } \\ {-{\bf c}^T T} & {1} \end{array}\right] \left[\begin{array}{c} {{\bf x}(k)} \\ {v(k)} \end{array}\right]+\left[\begin{array}{c} {\bf 0} \\ {T} \end{array}\right]r(k)\]

El polinomio característico de bucle cerrado del sistema incrementado se forma como:

\[{\mathit{\Delta}}_a\left(z\right)=\left| \begin{array}{cc} z{\bf I-A}_{\rm d}+{\bf b}_{\rm d}k^T & -{\bf b}_{\rm d}k_i \\ -{\bf c}^T_{\rm d}T & z-1 \end{array} \right|\]

donde\({\bf I}\) denota una matriz de identidad de orden\(n\).

A continuación, elegimos un polinomio característico deseado de\((n+1)\) orden, y realizamos el diseño de colocación de polos para el sistema incrementado. La ubicación del polo integrador en el\(z\) plano se puede seleccionar manteniendo a la vista los criterios de rendimiento deseados para el sistema de bucle cerrado.

Ejemplo\(\PageIndex{6}\)

El modelo de variable de estado discreto de un motor\(T=0.02\) o motores de CC se da como:

\[\left[ \begin{array}{c} i_{k+1} \\ {\omega }_{k+1} \end{array} \right]=\left[ \begin{array}{cc} 0.134 & -0.038 \\ 0.038 & 0.816 \end{array} \right]\left[ \begin{array}{c} i_k \\ {\omega }_k \end{array} \right]+\left[ \begin{array}{c} 0.863 \\ 0.053 \end{array} \right]V_k,\ \ {\omega }_k=\left[ \begin{array}{cc} 0 & 1 \end{array} \right]\left[ \begin{array}{c} i_k \\ {\omega }_k \end{array} \right]\]

La ley de control para el controlador PI de seguimiento se define como:

\[u_k=-k_1i_k-k_2{\omega }_k+k_iv_k\]

donde se\(v_{k} =v_{k-1} +T(r_{k} -\omega _{k} )\) describe la salida del integrador. El modelo de sistema incrementado para el diseño de colocación de postes mediante control integral se da como:

\[\left[ \begin{array}{c} i_{k+1} \\ {\omega }_{k+1} \\ v_{k+1} \end{array} \right]=\left[ \begin{array}{ccc} 0.134 & -0.038 & 0 \\ 0.038 & 0.816 & 0 \\ 0 & -0.02 & 1 \end{array} \right]\left[ \begin{array}{c} i_k \\ {\omega }_k \\ v_k \end{array} \right]+\left[ \begin{array}{c} 0.863 \\ 0.053 \\ 0 \end{array} \right]V_k+\left[ \begin{array}{c} 0 \\ 0 \\ 0.02 \end{array} \right]r_k\]

Las ubicaciones deseadas\(z\) de los polos del plano para un deseado\(\zeta=0.7\) se seleccionan como:\(z=e^{-1} ,\; e^{-1\pm j1}\).

Las ganancias del controlador, obtenidas usando el comando 'place' de MATLAB, se dan como:\(k_{1} =0.43,k_{2} =15.44,\; k_{i} =-297.79.\)

Una regla de actualización para la implementación del controlador en la computadora se da como:

\[u_k=-0.43i_k-15.44{\omega }_k+297.8v_k\]

\[v_k=v_{k-1}+0.02\left(r_k-{\omega }_k\right)\]

La respuesta escalonada del sistema de bucle cerrado se representa en la Figura 10.2.6. La respuesta escalonada del sistema de tiempo continuo (Ejemplo 9.1.1) se traza al lado. La salida en ambos casos alcanza el valor de unidad en estado estacionario en aproximadamente 0.12seg.

Figura\(\PageIndex{6}\): Control PI de seguimiento del modelo de motor de CC: respuesta de bucle cerrado para los sistemas analógicos y discretos.