2.2: El concepto contable
- Page ID
- 86333
La experiencia ha demostrado que el concepto contable es más útil cuando se aplica para dar cuenta de propiedades extensas, por lo que las “cosas” mencionadas al final del Capítulo 1 deberían interpretarse realmente como propiedades extensas. La figura\(\PageIndex{1}\) muestra un sistema cuyas interacciones con su entorno se muestran como transferencias de una propiedad extensa. Esta es una imagen útil para ayudarnos a visualizar lo que está sucediendo a medida que aplicamos el concepto contable.
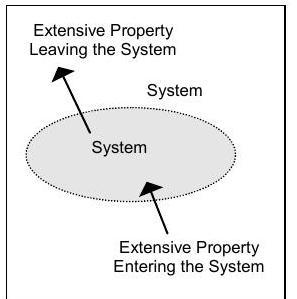
Figura\(\PageIndex{1}\): Las interacciones sistema-entorno se representan como transferencias de una propiedad extensa.
2.2.1 Forma de Tasa del Concepto Contable
La forma más general del concepto contable que vamos a utilizar es la forma de tasa. Este formulario es válido en cualquier instante en el tiempo. La forma de tarifa del principio contable para una propiedad extensa (EP) se puede escribir en palabras para cualquier sistema:
La tasa de acumulación de EP dentro del sistema en el tiempo\(t\) es igual a la tasa de transporte de EP al sistema en el tiempo\(t\) menos la tasa de transporte de EP fuera del sistema en el tiempo\(t\) más la tasa de generación (producción) de EP dentro del sistema en el tiempo\(t\) menos la tasa de consumo (destrucción) de EP dentro del sistema en el momento\(t\).
En un formato similar a la ecuación, las palabras se pueden presentar como
.png)
Figura\(\PageIndex{2}\): El principio de contabilidad tarifa-forma para una propiedad extensa expresado en palabras en forma de ecuación.
Si dejamos que el símbolo\(B\) represente una propiedad genérica extensa, podemos escribir esto de manera más compacta en símbolos:
\[ \frac{d}{dt} \underbrace{ B_{sys} } _{B \text{ inside the system} } = \underbrace{ \{ \dot{B}_{in} - \dot{B}_{out} \} } _{ \text{Transport of } B \text{ inside the system} } + \underbrace{ \{ \dot{B}_{gen} - \dot{B}_{cons} \} } _{\text{Generation/Consumption of } B \text{ inside the system} } \nonumber \]
Tenga en cuenta que todos los términos de esta ecuación se definen independientemente del concepto contable. El concepto contable gana su poder de su capacidad de relacionar estos diversos términos para cualquier sistema.
La forma de tasa de la ecuación contable, Ec. \(\PageIndex{1}\), se puede escribir incluso en una forma más compacta si introducimos la idea de transporte neto y generación neta:
\[ \begin{align} \frac{d}{dt} \underbrace{ B_{sys} } _{B \text{ inside the system} } &= \underbrace{ \{ \dot{B}_{in} - \dot{B}_{out} \} } _{ \text{Transport of } B \text{ inside the system} } + \underbrace{ \{ \dot{B}_{gen} - \dot{B}_{cons} \} } _{\text{Generation/Consumption of } B \text{ inside the system} } \nonumber \\ &= \quad \dot{B}_{in, net} + \dot{B}_{gen, net} \end{align} \nonumber \]
En esta notación, el primer término del lado derecho es positivo si hay más transporte hacia el sistema que fuera del sistema. Un valor negativo indica que hay más saliendo del sistema que entrando.
La gráfica a continuación muestra\(B_{sys}\) como una función del tiempo para un sistema.
.png)
a) ¿Cómo podría usar esta gráfica para explicar el significado del término\(\frac{dB_{sys}} {dt}\)?
b) ¿Dónde está\(B_{sys}\) aumentando? ¿Disminuyendo?
c) ¿Dónde es\(\frac{dB_{sys}} {dt}\) positivo? ¿Negativo?
d) ¿Cómo se relacionan sus respuestas a las partes b) y c)?
Debido a que las matemáticas son el lenguaje principal para nuestro análisis y una práctica mano corta para comunicar nuestras ideas, es importante entender claramente lo que significan los diversos símbolos y notación. Comenzando con la Ec. \(\PageIndex{1}\)y\(\PageIndex{2}\), es muy importante reconocer que el lado izquierdo y el lado derecho de cada una de estas ecuaciones representan cosas diferentes. La izquierda describe lo que está sucediendo dentro del sistema y describe cómo la cantidad de propiedad extensa\(B\) está aumentando o disminuyendo dentro del sistema. El lado derecho describe algo sobre la cantidad de propiedad extensa que\(B\) está cruzando el límite del sistema o se está consumiendo o generando dentro del sistema.
Físicamente, la derivada en el lado izquierdo de la Ec. \(\PageIndex{1}\)y\(\PageIndex{2}\) representa la tasa de cambio o acumulación de la extensa propiedad\(B_{sys}\) dentro del sistema en cualquier momento\(t\). Es la tasa de cambio de algo que está contenido dentro del sistema,\(B_{sys}\). Tenga en cuenta que es solo un derivado ordinario. Matemáticamente esto es correcto porque la cantidad de la propiedad extensa\(B\) dentro del sistema,\(B_{sys}\), es solo una función del tiempo, es decir\(B_{sys} (t)\). La derivada ordinaria de\(B_{sys}\) con respecto al tiempo,\(dB_{sys} / dt\), representa la tasa de cambio del\(B\) interior del sistema.
Si tuviera una gráfica que mostrara la cantidad de\(B\) dentro del sistema en función del tiempo, entonces\(dB_{sys} / dt\) representa la pendiente de la línea en cualquier momento deseado. Para evaluar esta derivada, debo hacer un seguimiento de todo el\(B\) interior del sistema en función del tiempo. Para determinar la tasa de cambio de\(B_{sys}\), debo poder calcular la derivada ordinaria o relacionar este término con otras cantidades medibles.
Matemáticamente, los términos en el lado derecho de la Ec. \(\PageIndex{1}\)y no\(\PageIndex{2}\) son derivados. Como se usa aquí, el punto sobre un símbolo no representa diferenciación. La notación “punto-arriba”\(\dot{B}\), representa una tasa de transporte, una interacción, entre el sistema y su entorno donde\(B\) fluye a través del límite del sistema o la velocidad a la que\(B\) se produce o consume dentro del sistema. Permítanme repetir esto una vez más para énfasis: no\(\dot{B}\) es un derivado.
Entonces, ¿qué es? “\(B\)con un punto encima de él” o "\(B\)punto”\(\dot{B}\), no representa una tasa de cambio de nada dentro del sistema. Representa la velocidad a la que la extensa propiedad\(B\) se transporta a través del límite de un sistema o se genera (o consume) dentro de un sistema. En teoría, el conocimiento acerca no\(\dot{B}\) está relacionado con la cantidad de\(B\) dentro del sistema. (¡Sí, sí, sí! Sé que se puede relacionar con lo que hay dentro del sistema a través del principio contable, pero ese es el punto. \(\dot{B}\)y\(dB_{sys} / dt\) son dos cosas distintas que se definen y se pueden medir independientemente entre sí. El concepto contable nos muestra cómo se pueden relacionar entre sí.)
Tomemos un ejemplo sencillo para tratar de entender las diferencias. Asume que tu mamá te compra una caja de galletas de animales. (¿A quién no le encantan las galletas de animales?) En cuanto consigues la caja, empiezas a comer las galletas de animales. Tu celoso hermano y hermana menores empiezan a hacer un seguimiento de las galletas para ver si van a conseguir alguna.
Tu hermano es bastante activo y le cuesta quedarse quieto, así que cada cinco minutos tu hermano vuelve corriendo a la habitación, te quita la caja y cuenta el número de galletas que hay en la caja. Entonces huye y no te ve comerte las galletas. Para ayudarlo a recordar, anota estos números como una tabla que muestra el número de galletas en la caja a intervalos de cinco minutos, es decir, a 0, 5, 10 min, etc.
Tu hermana, por otro lado, es mucho menos combativa. Ella te ve comer las galletas y solo cuenta cuántas galletas sacas de la caja durante cada intervalo de 5 minutos, 0 min a 5 min, 5 min a 10 min, etc. Desafortunadamente, tus hermanos tampoco se llevan bien así que no comparten información entre ellos.
Los resultados de sus esfuerzos se muestran a continuación en la tabla.
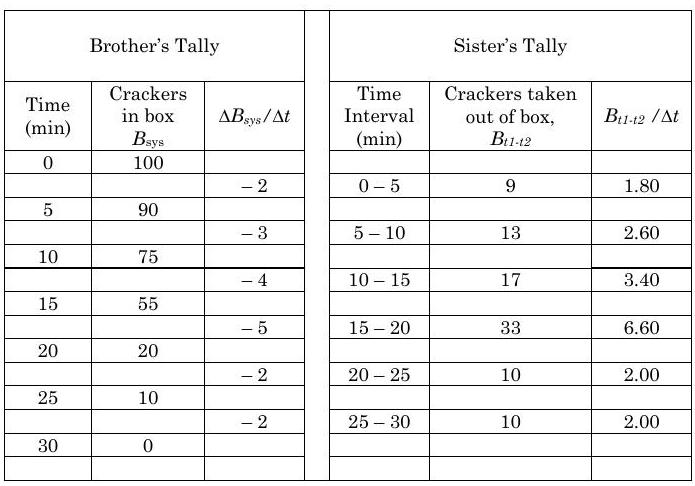
Si se llama al número de galletas en la caja\(B\) entonces tu hermano puede trazar una gráfica que muestre una serie de puntos de la función\(B_{sys}(t)\) para la caja. Puede usar esta información para calcular la tasa promedio de cambio para cualquier intervalo usando la fórmula\( (dB_{sys} / dt) _{average} = \Delta B / \Delta t\) para cualquier intervalo de 5 minutos. Observe que todo lo que tiene que saber para calcular la tasa de cambio es cuántas galletas hay en la caja en función del tiempo. Desafortunadamente, tu hermano no tiene idea a dónde van las galletas a menos que vea que las sacas.
Ahora tu hermana no tiene idea de cuántas galletas hay en la caja, pero tiene la información suficiente para calcular la tasa promedio de transporte de las galletas fuera de la caja (cuántas comiste por minuto). Ella hace esto dividiendo el número de galletas que sacaste en un intervalo de cinco minutos, digamos\(B_{0-5}\), y dividiéndolo por el intervalo de tiempo, 5 minutos, es decir,\(\dot{B}_{out, average} = B_{0-5} / \Delta t\). Observe que todo lo que su hermana necesitaba para calcular la tasa de transporte fuera de la caja era enfocarse en el límite de su sistema (la caja) y contar cuántas crackers la cruzaron en cualquier periodo de tiempo dado. Esto no es un derivado de nada; es una tarifa de transporte, pero no un derivado. Ella sabe la tasa promedio a la que las galletas se transportaron fuera de la caja, pero no sabe nada sobre la tasa de cambio de las galletas dentro de la caja.
Tu hermana y tu hermano se intrigan tanto con sus medidas que se olvidan totalmente de comer cualquier galletita; sin embargo, sí deciden comparar su información. Para su sorpresa, descubren lo siguiente:
\[ \left( \frac{dB_{sys}}{dt} \right) _{average} \neq - \dot{B}_{out, average} \nonumber \]
La tasa promedio de cambio de las galletas dentro de la caja no fue igual a la tasa promedio de transporte de las galletas fuera de la caja. ¿Qué pasó?
Bueno, parece que alguien se olvidó de notar el pequeño ratón en la caja que estaba consumiendo galletas a la tasa promedio de\(\dot{B}_{mouse, average}\). Si tenemos en cuenta el ratón comiendo (consumiendo) las galletas vemos que
\[ \left( \frac{dB_{sys}}{dt} \right) _{average} = - \dot{B}_{out, average} - \dot{B}_{mouse, average} \nonumber \]
deben aplicarse a este sistema. Esta ecuación podría utilizarse para resolver la tasa de consumo promedio a la que el ratón se comió las galletas.
De este ejemplo se pueden aprender varias cosas.
- Todos los términos de la ecuación contable anterior tienen definiciones independientes y, en las mejores circunstancias, podrían medirse directamente.
- Estos términos también se pueden relacionar a través del principio contable aplicado al sistema apropiado (la caja) para la propiedad correspondiente (número de galletas en la caja), y el principio contable se puede utilizar para resolver por un término desconocido.
- El único término que puede considerarse derivado es el término del lado izquierdo. Las tarifas de transporte y consumo del lado derecho no son derivadas y no tienen relación directa con la tasa de cambio del\(B\) interior del sistema salvo a través del concepto contable aplicado correctamente a un sistema.
- La ecuación contable es más útil cuando podemos decir algo a priori sobre los términos de consumo y generación. Si hubiéramos sabido que la caja estaba libre de ratón, solo necesitaríamos observar la tasa de transporte de las cookies fuera del sistema para predecir la tasa de cambio de las cookies dentro del sistema. Como veremos en breve, muchas leyes físicas importantes han alcanzado este estatus precisamente porque la evidencia empírica nos permite decir algo sobre los términos de consumo y generación.
Otra forma de entender la distinción entre\(dB/dt\) y\(\dot{B}\) es considerar qué sucede cuando cada uno se integra a lo largo de un intervalo de tiempo. Cuando\(B\) con un punto sobre él se multiplica por\(dt\), el resultado no es el diferencial estándar\(dB\) sino un nuevo símbolo\(\delta B\) que representa no un “cambio en” sino una “pequeña cantidad de”:
\[ \begin{align*} \delta B &= \dot{B} dt \\ &= \text{small amount of B} \\ &= \text{an inexact differential because } B \text{ is not a single-valued function of } t. \end{align*} \nonumber \]
Por otro lado, recordará de su cálculo que la interpretación de la derivada\(dB/dt\) es
\[ dB = \frac{dB}{dt} dt \quad\quad \text{because } \frac{dB}{dt} = \lim_{\Delta t \to 0} \frac{B(t + \Delta t) - B(t)}{\Delta t} \nonumber \]
donde\(dB\) equivale a “un pequeño cambio” en\(B(t)\), una función de un solo valor.
Ahora la integral de la derivada ordinaria con respecto al tiempo es el cambio\(B\) entre los dos tiempos:
\[ \int\limits_{t_1}^{t_2} \frac{dB}{dt} \, dt = \int\limits_{B(t_1)}^{B(t_2)} dB = B(t_2) - B(t_1) = \Delta B \nonumber \]
La integración de\(\dot{B}\) con respecto al tiempo en el mismo intervalo de tiempo es una cantidad de\(B\), no un cambio en\(B\), como se muestra a continuación:
\[ \int\limits_{t_1}^{t_2} \dot{B} \, dt = \int\limits_{t_1}^{t_2} \delta B = B_{t_1 \to t_2} \nonumber \]
Tenga cuidado de estar seguro de que comprende las diferencias entre estas dos últimas ecuaciones y que puede realizar estas integraciones.
2.2.2 Forma de tiempo finito (integrado) del concepto contable
Hay muchas ocasiones en las que nos interesa un sistema que ha sido sometido a un proceso durante un intervalo de tiempo específico. En estos casos, es posible integrar la forma de tasa para obtener una forma de tiempo finito. La figura\(\PageIndex{5}\) muestra una imagen que es útil para interpretar la forma de tiempo finito del concepto contable. Como puede ver, el sistema existe en dos estados diferentes y está conectado por un proceso.
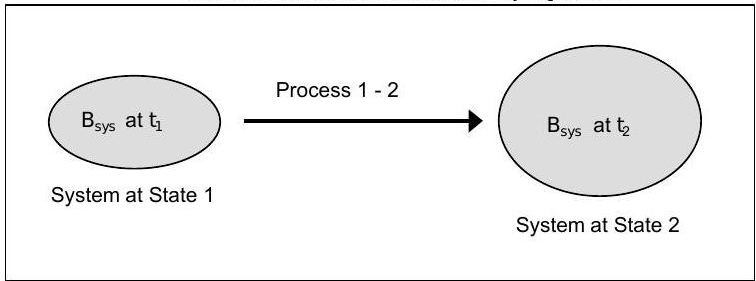
Figura\(\PageIndex{5}\): Sistema en proceso del Estado 1 al Estado 2
En palabras, la forma de tiempo finito del concepto contable se escribe de la siguiente manera:
.png)
Figura\(\PageIndex{6}\): La forma de tiempo finito del concepto contable expresada en palabras en forma de ecuación.
En símbolos, la forma de tiempo finito se escribe de la siguiente manera:
\[ \begin{align} B_{sys} (t_2) - B_{sys} (t_1) &= \{ B_{in} - B_{out} \} + \{ B_{gen} - B_{cons} \} \nonumber \\ \Delta B_{sys} &= B_{in, net} + B_{gen, net} \end{align} \nonumber \]
El significado de cada uno de estos símbolos se puede determinar por comparación con la declaración de palabras.
Ahora ponte a prueba. Comenzando con la Ec. \(\PageIndex{2}\)y utilizando los resultados de la Ec. \(\PageIndex{3}\)y\(\PageIndex{4}\), mostrar los pasos para desarrollar la Ec. \(\PageIndex{5}\).


