Saltar al contenido principal
LibreTexts Español

6.1: ¿Por qué esta cosa está girando?

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    86298

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Cualquiera que haya cambiado una llanta desinflada, haya usado una llave inglesa, arroje un Frisbee, colgado de una rama de árbol o empujado una caja grande sabe algo sobre la tendencia de que los objetos giren o resistan la rotación. El momento angular es la extensa propiedad física relacionada con este fenómeno. Antes de que podamos desarrollar la conservación de la relación de momento angular, debemos introducir varios conceptos para describir el movimiento angular y el momento de una fuerza.

    Considerar:

    ¿Cuál es el propósito de una barra “tramposa” aplicada a una llave inglesa? (Una barra “tramposa” es un trozo de tubo deslizado sobre el extremo de una llave para extender su longitud).

    ¿Dónde está el mejor lugar para empujar un archivador sobre rodillos? ¿Cómo juzgó mejor?

    Para refrescar tu memoria, imagina que tu auto tiene una llanta pinchada y debes cambiarla (Ver Figura\(\PageIndex{1}\)). Para cambiar la llanta, primero levanta la llanta del suelo usando un gato para automóvil. A continuación, colocas la plancha de llanta sobre una tuerca y tratas de aflojarla. En el boceto, la fuerza\(\mathbf{F}\) actúa sobre el hierro del neumático en el punto\(P\), el eje del neumático está en el punto\(O\) y la tuerca se ubica en el punto\(N\).

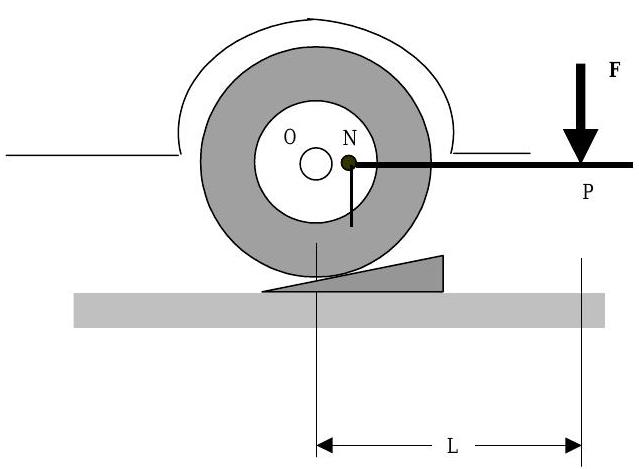
    Una llanta se mantiene ligeramente alejada del suelo por una cuña. Una tuerca N de la llanta está siendo aflojada por una plancha de neumático, que se mantiene paralela al suelo. Se aplica una fuerza hacia abajo F al extremo libre de la plancha del neumático, en el punto P ubicado a una distancia de L del centro del neumático.

    Figura\(\PageIndex{1}\): Cambio de una llanta.

    Si has tenido suerte en la vida, puedes ser un novato en el cambio de llantas, y descubrirás que la llanta gira cuando empujas la plancha de la llanta. Un conductor con menos suerte y más experiencia cambiando llantas podría solo levantar la llanta parcialmente o insertar una cuña para evitar que la llanta gire. Los cambiadores de neumáticos experimentados saben que nuestra capacidad para aflojar la tuerca depende tanto de la fuerza\(\mathbf{F}\) como de su punto de aplicación (punto\(P\)). También saben que la efectividad de la fuerza aplicada\(\mathbf{F}\) es menor si se aplica en ángulo con el hierro del neumático.

    ¿Qué pasaría si la fuerza se aplicara en un momento\(N\)? ¿Serías capaz de aflojar la tuerca? ¿La llanta giraría?

    6.1.1 Momento de una fuerza alrededor de un punto

    Para cuantificar la capacidad de la fuerza para rotar el neumático necesitamos una cantidad física que tenga en cuenta la magnitud y dirección de la fuerza así\(\mathbf{F}\) como su punto de aplicación. La cantidad que deseamos es el momento de una fuerza alrededor de un punto.

    El momento de una fuerza\(\mathbf{F}\) alrededor de un punto\(\bf{O}\) es el vector (o cruz) producto del vector de posición\(\mathbf{r}\) y la fuerza\(\mathbf{F}\):

    \[ \mathbf{M}_O = \mathbf{r} \times \mathbf{F} \nonumber \]

    donde\(\mathbf{r}\) está el vector de posición que se extiende desde el punto\(O\) hasta el punto de aplicación de la fuerza (Ver Figura\(\PageIndex{2}\)).

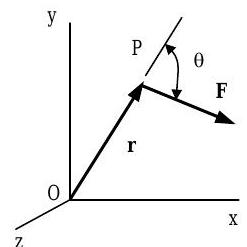
    Un sistema de coordenadas tridimensional con ejes x, y y z contiene un punto P cuya ubicación relativa al origen O viene dada por el vector r. Una fuerza representada como vector F se aplica al punto P. El menor de los dos ángulos hechos por la línea de acción de F con r viene dado por theta.

    Figura\(\PageIndex{2}\): Momento calculador de una fuerza\(\mathbf{F}\) alrededor de un punto\(O\).

    Cuando el vector de posición\(\mathbf{r}\) y el vector de fuerza\(\mathbf{F}\) se escriben en términos de sus componentes como la\[\mathbf{r} = x \mathbf{i}+y \mathbf{j}+z \mathbf{k} \quad \text { and } \quad \mathbf{F}=F_{x} \mathbf{i}+F_{y} \mathbf{j}+F_{z} \mathbf{k} \nonumber \] Ec. \((\PageIndex{1})\)se evalúa de la siguiente manera usando operaciones estándar de productos cruzados:\[\begin{align} \mathbf{M}_{o} &=\mathbf{r} \times \mathbf{F}=\left| \begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x & y & z \\ F_{x} & F_{y} & F_{z} \end{array}\right| \nonumber \\[4pt] &=\mathbf{i}\left|\begin{array}{cc} y & z \\ F_{y} & F_{z} \end{array}\right|-\mathbf{j}\left|\begin{array}{cc} x & z \\ F_{x} & F_{z} \end{array}\right|+\mathbf{k}\left|\begin{array}{cc} x & y \\[4pt] F_{x} & F_{y} \end{array}\right| \\ &=\left(y F_{z}-z F_{y}\right) \mathbf{i}-\left(x F_{z}-z F_{x}\right) \mathbf{j}+\left(x F_{y}-y F_{x}\right) \mathbf{k} \nonumber \end{align} \nonumber \]

    Si nos limitamos al movimiento en el\(x \text{-} y\) plano (movimiento plano), el único componente de\(\mathbf{M}_O\) con un valor distinto de cero es el\(z\) -componente, el último término en el lado derecho de la Ec. \((\PageIndex{3})\).

    Desde nuestro conocimiento de vectores, podemos decir varias cosas sobre este resultado:

    • El vector de posición\(\mathbf{r}\) y el vector de fuerza\(\mathbf{F}\) se encuentran en un plano.
    • El momento\(\mathbf{M}_O\) de la fuerza\(\mathbf{F}\) sobre el punto\(O\) es un vector (ver Eq. \((\PageIndex{3})\)).
    • La línea de acción del vector momento\(\mathbf{M}_{O}\) es normal (perpendicular) al plano que contiene ambos\(\mathbf{r}\) y\(\mathbf{F}\).
    • El punto de aplicación del vector momento\(\mathbf{M}_{O}\) está en el punto\(O\), el punto sobre el que estamos tomando el momento.
    • El sentido de la dirección del momento\(\mathbf{M}_{O}\) y el sentido de la rotación que podría impartir pueden ser descritos por la regla de la derecha de varias maneras (Ver Figura\(\PageIndex{3}\)):
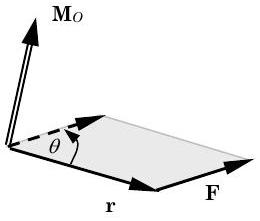
      Los vectores r, apuntando a la derecha y fuera de la página, y F, apuntando a la derecha y dentro de la página, se encuentran en un plano paralelo al suelo. La cola de r se ubica en el punto O y la cola de F se coloca en la cabeza de r. Se sombrea un paralelogramo formado por 2 instancias cada una de r y F colocadas cabeza a cola, con el menor de los dos ángulos entre un vector r y una F adyacente designada theta. Un vector M_O, que indica el momento sobre el punto O, apunta hacia arriba y hacia la página.
      Figura\(\PageIndex{3}\): Sentido de dirección del\(\mathbf{M}_O\) uso de la regla de la derecha.
      • Alinee los dedos de su mano derecha en la dirección del vector de posición\(\mathbf{r}\) y rizarlos en la dirección de la fuerza\(\mathbf{F}\). Ahora tu pulgar apunta en la dirección del momento\(\mathbf{M}_{O}\) y tus dedos se curvan para mostrar la sensación de rotación por el momento\(\mathbf{M}_{O}\).
      • Imagina un vector deslizante\(\mathbf{r}\) o\(\mathbf{F}\) hasta que estén cola a cola. Alinea los dedos de tu mano derecha en la dirección del vector de posición\(\mathbf{r}\) y riza tus dedos en la dirección de la fuerza\(\mathbf{F}\). Tus dedos curvados ahora indican el sentido de rotación por el momento\(\mathbf{M}_{O}\) y tu pulgar apunta en la dirección del momento\(\mathbf{M}_{\text {O}}\).
      • Enrilla los dedos de tu mano derecha y apunta el pulgar de tu mano derecha en la dirección del momento\(\mathbf{M}_{O}\). La dirección en la que se rizan tus dedos es el sentido de rotación por el momento\(\mathbf{M}_{O}\).
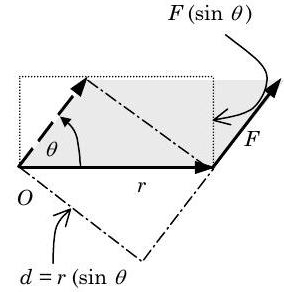
    • La magnitud del vector momento\(\mathbf{M}_{O}\) es la raíz cuadrada del producto punto de\(\mathbf{M}_{O}\) consigo mismo y se calcula de la siguiente manera:\[\begin{array} M M_{O} &=\left|\mathbf{M}_{o}\right|=\left(\mathbf{M}_{O} \cdot \mathbf{M}_{O}\right)^{1 / 2} \\ &=\left[\left(y F_{z}-z F_{y}\right)^{2}+\left(x F_{z}-z F_{x}\right)^{2}+\left(x F_{y}-y F_{x}\right)^{2}\right]^{1 / 2} \end{array} \nonumber \] También se puede calcular usando la relación\[M_{o}=\left|\mathbf{M}_{o}\right|=|\mathbf{r}||\mathbf{F}| \sin \theta=r F(\sin \theta) \nonumber \] donde\(\theta\) está el ángulo entre las líneas de acción de los vectores\(\mathbf{r}\) \(\mathbf{F}\)y se mide como si\(\mathbf{r}\) y\(\mathbf{F}\) se colocaran cola a cola. Un ángulo positivo satisface la regla de la derecha como se describió anteriormente. Eq. \(( \PageIndex{5})\)se puede interpretar como el área de un paralelogramo formado por los vectores\(\mathbf{r}\) y\(\mathbf{F}\) (Ver Figura\(\PageIndex{4}\)).
      El vector r, con su cola en el punto O, apunta a la derecha. El vector F, con su cola a la cabeza del vector r, apunta hacia arriba y hacia la derecha. Un paralelogramo está formado por dos instancias cada una de r y F, colocadas cabeza a cola. El menor de los dos ángulos del paralelogramo es theta. El área de paralelogramo es equivalente al área de un rectángulo de base r y altura F (sin theta), o un rectángulo de base d = r (sin theta) y altura F.
      Figura\(\PageIndex{4}\): Interpretación de la magnitud de\(\mathbf{M}_O\) como área.

      Dos rectángulos adicionales que se muestran en la Figura\(\PageIndex{4}\) tienen áreas iguales en magnitud al área sombreada. El rectángulo de largo\(d_{\perp}\) y ancho\(F\) tiene un área de\[\begin{align} M_{O} &=(r \sin \theta) F \nonumber \\ &=d_{\perp} \times F \quad=\underbrace{\left[\begin{array}{c} \text { Shortest distance } \\ \text { between point } O \\ \text { and the line-of-action } \\ \text { of force } \mathbf{F} \end{array}\right]}_{\text {Often called the "lever arm" }} \times\left[\begin{array}{c} \text { Magnitude } \\ \text { of } \\ \text { force } \mathbf{F} \end{array}\right] \end{align} \nonumber \] El rectángulo de largo\(r\) y ancho\(F \sin \theta\) tiene un área de\[\begin{align} M_{O} &=r(F \sin \theta) \nonumber \\ &=r \times F_{\perp}=\left[\begin{array}{c} \text { Magnitude } \\ \text { of the } \\ \text { position vector } \mathbf{r} \end{array}\right] \times\left[\begin{array}{c} \text { Component of force } \mathbf{F} \\ \text { that is } \perp \text { to } \\ \text { the line-of-action of } \mathbf{r} \end{array}\right] \end{align} \nonumber \] Para la mayoría de los casos con movimiento bidimensional (plano), lo encontrarás usando Eqs. \((\PageIndex{6})\)o\((\PageIndex{7})\) es mucho más simple que usar las matemáticas formales de productos cruzados.

    Pon a prueba tu comprensión

    Para cada uno de los siguientes casos bidimensionales, determine la magnitud y dirección [en sentido horario (CW) o antihorario (CCW)] del momento de fuerza\(\mathbf{F}\) alrededor del punto\(O\):

    a)

    Una barra horizontal de 4 metros de largo tiene el punto O en su extremo izquierdo. Una fuerza de 50 N dirigida hacia arriba y hacia la derecha, a 20 grados de la vertical, se aplica en el extremo derecho de la barra.

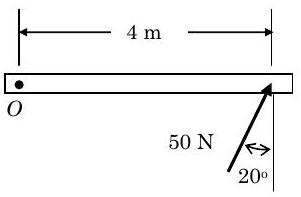
    Figura\(\PageIndex{5}\): Se aplica una fuerza en ángulo a un extremo de una barra.

    b)

    Una barra horizontal de 4 metros tiene el punto O en su punto final izquierdo. Una fuerza de 50 N dirigida hacia abajo y hacia la izquierda a 80 grados de la vertical se aplica al extremo derecho de la barra.

    Figura\(\PageIndex{6}\): Se aplica una fuerza en ángulo a un extremo de una barra.

    c)

    Un objeto está compuesto por dos barras horizontales con el extremo derecho de la barra superior conectado al extremo izquierdo de la barra inferior. El punto O es el punto más a la izquierda del conjunto. Una fuerza de 50 N dirigida hacia arriba y hacia la derecha a 45 grados de la vertical se aplica a un punto 4 metros a la derecha y 1 metro por debajo de O.

    Figura\(\PageIndex{7}\): Se aplica una fuerza en ángulo a un extremo de un cuerpo rígido.

    Contestar

    a)\(187.9 \ \mathrm{N} \cdot \mathrm{m CCW}\)

    b)\(34.73 \ \mathrm{N} \cdot \mathrm{m CW}\)

    c)\(176.8 \ \mathrm{N} \cdot \mathrm{m CCW}\)

    6.1.2 Momento de una pareja de fuerza

    Existe un tipo especial de sistema de fuerza externa llamado par de fuerzas. Un par de fuerzas consiste en dos fuerzas externas que tienen igual magnitud, líneas de acción paralelas y sentido opuesto (Ver Figura\(\PageIndex{8}\)). Así, un par de fuerzas resulta en una fuerza neta cero en un sistema. O declarando esto de otra manera, un par de fuerzas transfiere impulso lineal cero a un sistema. Sin embargo, un rápido examen de la figura muestra que el par de fuerza de hecho intenta girar o rotar el sistema.

    Un cuerpo irregularmente curvado contiene tres puntos O, O' y O”. El vector de fuerza F1 representa una fuerza aplicada a algún punto del cuerpo, con magnitud F. El vector de fuerza F2 representa una fuerza aplicada a algún otro punto del cuerpo, también de magnitud F y a lo largo de la misma línea de acción que F1 mientras apunta en dirección opuesta. La distancia entre las líneas de acción de las fuerzas viene dada por d.

    Figura\(\PageIndex{8}\): Una pareja de fuerza.

    El momento de un par de fuerzas alrededor del punto se\(O\) puede calcular con referencia a la Figura de la\(\PageIndex{8}\) siguiente manera:\[ \begin{align} \mathbf{M}_{O, \text { couple }} &= \mathbf{M}_{O, \ F_{1}} + \mathbf{M}_{O, \ F_{2}} \nonumber \\ &= \left( \mathbf{r}_{1} \times \mathbf{F}_{1} \right) + \left( \mathbf{r}_{2} \times \mathbf{F}_{2}\right) \quad\quad\quad \text { where } \left| \mathbf{F}_{1} \right| = \left|\mathbf{F}_{2}\right| = F \nonumber \\ &= \left[ \left( d_{\perp, 1} \times F_{1}\right) \,\, \mathrm{CCW} \right] + \left[ \left( d_{\perp, 2} \times F_{2}\right) \,\, \mathrm{CW} \right] \\ & = \left[ -\left( d_{\perp, 1} \times F_{1}\right) \quad + \quad \left(d_{\perp, 2} \times F_{2}\right) \right] \quad \text { CW } \nonumber \\ &= d \times F \quad \text { CW } \quad\quad\quad\quad\quad\quad\quad \text { where } d=\left| d_{\perp, 1}-d_{\perp, 2}\right| \nonumber \\ {} \nonumber \\ \mathbf{M}_{O, \text { couple }} &= d \times F \text{ in a CW direction} \nonumber \end{align} \nonumber \]

    Tenga en cuenta que si hubiéramos calculado el momento del par de fuerza que se muestra en la Figura\(\PageIndex{8}\) sobre punto\(O'\) o punto\(O''\) habríamos encontrado exactamente el mismo resultado. Así, el momento de una pareja no parece estar atado a un punto en particular, a diferencia de lo que encontramos con el momento de una fuerza sobre un punto.

    Podemos decir lo siguiente sobre un par de fuerzas con fuerza\(\mathbf{F}\) y una distancia que\(d\) separa las líneas de acción de las fuerzas:

    • Las líneas de acción de las dos fuerzas en una pareja de fuerzas se encuentran en el mismo plano.
    • Un par de fuerzas no transfiere ningún momento lineal neto a un sistema.
    • El momento producido por un par de fuerzas es un vector\(\mathbf{M}_{\text {couple}}\).
    • La línea de acción del vector momento\(\mathbf{M}_{\text {couple}}\) es normal (perpendicular) al plano que contiene el par de fuerzas.
    • El punto de aplicación del vector momento\(\mathbf{M}_{\text {couple}}\) puede estar en cualquier punto del plano de la pareja. Debido a que el punto de aplicación es libre de moverse, este tipo de vector a veces se llama vector libre.
    • El sentido del vector de momento\(\mathbf{M}_{\text {couple can be obtained from ob. }}\) que sirve la dirección de rotación que el par de fuerzas podría impartir. La dirección del vector momento se puede encontrar enrollando los dedos de tu mano derecha para que coincidan con el sentido de la pareja de fuerza y alineando tu pulgar a lo largo de la línea de acción. Tu pulgar ahora apunta en dirección para el vector momento\(\mathbf{M}_{\text {couple. }}\).
    • La magnitud del vector momento\(\mathbf{M}_{\text {couple is equal to the product }}\) de la magnitud de uno de los vectores de fuerza y la distancia más corta entre las líneas de acción,\(d\):\[M_{\text {couple}} = \left| \mathbf{M}_{\text {couple}}\right| = d \times |\mathbf{F}| = d \times F \nonumber \]

    Frecuentemente encontraremos sistemas donde la distribución de fuerzas en alguna porción del límite se parece a la que se muestra en la Parte (a) de la Figura\(\PageIndex{9}\). En la mitad superior del límite, las fuerzas son compresivas (empujan sobre el sistema), y en la mitad inferior del límite, las fuerzas son de tracción (tiran del sistema). Si cada fuerza en la mitad superior tiene una imagen especular de sentido opuesto en la mitad inferior, esta distribución representa un par y la fuerza neta en el límite es cero; sin embargo hay un momento neto debido a la pareja como se muestra en la Parte (b) de la Figura\(\PageIndex{9}\). También habrá ocasiones en las que la distribución de la fuerza en el límite sea en realidad la suma de una pareja y una fuerza neta.

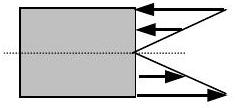    Un bloque experimenta a una pareja distribuida en su lado derecho. Para la mitad superior del bloque la fuerza distribuida se dirige hacia la izquierda, y para la mitad inferior la fuerza distribuida, distribuida simétricamente hacia la parte superior, se dirige hacia la derecha.a) Pareja distribuida que actúa sobre el límite
    El bloque de la parte A de la figura tiene su pareja distribuida reemplazada por una sola flecha curva que representa el momento equivalente.

    b) Momento equivalente debido a pareja distribuida

    Figura\(\PageIndex{9}\): Momento de una pareja distribuida.
    Pon a prueba tu comprensión

    Calcular la magnitud y la dirección (CW o CCW) para el momento neto sobre el punto\(O\):

    El punto O se encuentra en un cuerpo de forma irregular. 4 pies por encima de O, se aplica una fuerza de 100 lbf hacia la derecha. 4 pies a la derecha de O, se aplica una fuerza de 50 lbf hacia arriba. Se aplica al cuerpo cierta distancia a la derecha de O, un par de fuerzas con magnitud 75 lbf y una distancia de 2 pies separando las fuerzas.

    Figura\(\PageIndex{10}\): Las fuerzas puntuales y un par de fuerzas se aplican a una forma curva.

    This page titled 6.1: ¿Por qué esta cosa está girando? is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Donald E. Richards (Rose-Hulman Scholar) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.