6.2: Cuatro preguntas

6.2.1 ¿Qué es el momento angular?

En el Capítulo 5, mostramos que el momento lineal\(\mathbf{P}\) de una partícula con masa\(m\) y velocidad\(\mathbf{V}\) es el producto de la masa de la partícula y la velocidad de la partícula, e.g\(\mathbf{P}=\mathrm{mV}\). El momento angular de una partícula con respecto al punto\(\mathbf{O}\) es el vector (cruz) producto del vector de posición\(\mathbf{r}\) de la partícula con respecto al punto\(O\) y el momento lineal de la partícula\(\mathbf{P}\) (Ver Figura\(\PageIndex{1}\)):\[\mathbf{L}_{0} = \mathbf{r} \times \mathbf{P}=\mathbf{r} \times(m \mathbf{V}) \nonumber \]

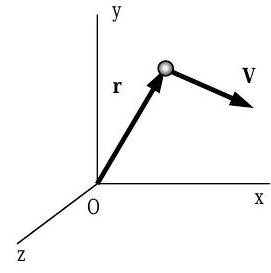
Figura\(\PageIndex{1}\): Cálculo del momento lineal de una partícula.

Es importante reconocer que el momento angular, al igual que el impulso lineal, es un vector, tiene tanto magnitud como dirección. Las dimensiones del momento angular son\([\mathrm{L}]^{2} [\mathrm{M}] [\mathrm{T}]^{-1}\). Las unidades típicas en el sistema SI son\(\mathrm{kg} \cdot \mathrm{m}^{2} / \mathrm{s}\) o\(\mathrm{N} \cdot \mathrm{m} \cdot \mathrm{s}\) y en el sistema USCS son\(\mathrm{lbm} \cdot \mathrm{ft}^{2} / \mathrm{s}\) o\(\mathrm{lbf} \cdot \mathrm{ft} \cdot \mathrm{s}\).

El momento angular específico para la partícula se puede calcular como el momento angular por unidad de masa:\[\mathbf{l}_{0}=\frac{\mathbf{L}_{0}}{m}=\mathbf{r} \times \mathbf{V} \nonumber \] Las dimensiones del momento angular específico son\( [\mathrm{L}]^{2} [\mathrm{~T}]^{-1} .\)

6.2.2 ¿Cómo se puede almacenar el momento angular en un sistema?

Para un sistema de partículas, el momento angular del sistema con respecto al punto\(O\) es la suma del momento angular de cada partícula en el sistema:\[\begin{align} \mathbf{L}_{O, \text{ sys}} &= \sum_{j=1}^{n} \mathbf{L}_{O, \ j} = \sum_{j=1}^{n}\left(\mathbf{l}_{o} m\right)_{j} \nonumber \\ &= \sum_{j=1}^{n} \left(\mathbf{r}_{j} \times \mathbf{V}_{j}\right) m_{j} \end{align} \nonumber \]

Para un sistema continuo, la suma se sustituye por una integral sobre el volumen del sistema:\[\mathbf{L}_{O, \text{ sys}} = \int\limits_{M_{\text{sys}}} \mathbf{I}_{o} \ dm = \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}}(\mathbf{r} \times \mathbf{V}) \rho \ d V\kern-0.8em\raise0.3ex- \nonumber \] Debido a la cinemática que describe el movimiento de un sistema, la evaluación de esta integral puede ser muy difícil. En este capítulo, solo consideraremos dos tipos de movimiento para los cuales esta integral puede evaluarse fácilmente: la traslación y la rotación alrededor de un eje fijo, centroidal. Una investigación más detallada del momento angular para el movimiento general se retrasará hasta un curso posterior, es decir, ES 204 — Análisis de Sistemas Mecánicos.

Movimiento plano de un sistema plano

En nuestras aplicaciones de momento angular a un sistema, nos limitaremos al movimiento plano de un sistema plano. Un sistema plano es un sistema que tiene un plano de simetría que contiene el centro de masa del sistema. El movimiento plano como se describe en la Sección 5.1.2 requiere que el plano de simetría del sistema y el\(x \text{-} y\) plano permanezcan paralelos en todo momento.

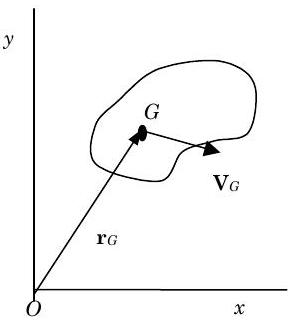
Figura\(\PageIndex{2}\): Sistema plano con traslación.

Un sistema plano con traslación

Cuando un sistema está traduciendo cada punto en el sistema tiene la misma velocidad,\(\mathbf{V}=\mathbf{V}_{\mathbf{x}} + \mathbf{V}_{\mathbf{y}}\). Para calcular el momento angular del sistema sobre el punto\(\mathrm{O}\), debemos evaluar la Ec. \(\PageIndex{4}\)de la siguiente manera:

\[ \begin{array}{ll} \mathbf{L}_{0, \text{ sys}} &= \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} (\mathbf{r} \times \mathbf{V}) \rho \ d V\kern-0.8em\raise0.3ex- & \left| \begin{array}{l} \mathbf{V} \text{ comes outside the} \\ \text{integral because} \\ \text{it is a constant.} \end{array} \right. \\[4pt] &= \left( \int\limits_{\ V\kern-0.5em\raise0.3ex-_{\text{sys}}} \mathbf{r} \rho \ d V\kern-0.8em\raise0.3ex- \right) \times \underbrace{ \mathbf{V} }_{\begin{array}{c} \mathbf{V}_G = \mathbf{V} \\ \text{since} \\ \text{translation} \end{array}} & \left| \begin{array}{l} \text{The integral within () can be} \\ \text{rewritten in terms of the} \\ \text{center of mass (Section } 5.1.2 \text{)} \end{array} \right. \\ &= \left( m_{\text{sys }} \mathbf{r}_G \right) \times \mathbf{V}_G & \left| \begin{array}{l} \mathbf{r}_G \text{ is the position vector of the} \\ \text{center of mass with respect to} \\ \text{point } O. \end{array} \right. \\[4pt] &= m_{\text{sys}} \left( \mathbf{r}_G \times \mathbf{V}_G \right) & \end{array} \nonumber \]

Así, el momento angular de un sistema plano de traslación es igual al producto de la masa del sistema y el producto cruzado de\(\mathbf{r}_{G}\) y\(\mathbf{V}_{G}\), la posición y el vector de velocidad, respectivamente, del centro de masa del sistema.

Pon a prueba tus conocimientos

(a) Comenzando con el resultado en la Ec. \(\PageIndex{5}\), prueban que la siguiente expresión es correcta para un sistema abierto:\[\frac{d \mathbf{L}_{0, \text{ sys}}}{dt} = \frac{d}{d t}\left[ m_{\text{sys}} \left(\mathbf{r}_{G} \times \mathbf{V}_{G}\right) \right] = \left(\mathbf{r}_{G} \times \mathbf{V}_{G}\right) \frac{d m_{\text{sys}}}{d t} + m_{\text{sys}} \left(\mathbf{r}_{G} \times \frac{d \mathbf{V}_{G}}{d t}\right) \nonumber \] ¿Qué pasó con\(m_{\text{sys}} \left(\dfrac{d \mathbf{r}_{G}}{d t} \times \mathbf{V}_{G}\right)\)?

(b) El bloque mostrado en la figura tiene una masa de\(50 \mathrm{~kg}\) y se traslada a la derecha con una velocidad de\(10 \mathrm{~m} / \mathrm{s}\). Determinar la magnitud y dirección de (a) el momento lineal del sistema; (b) el momento angular del sistema con respecto al punto\(A\), (c) el momento angular del sistema con respecto al punto\(B\), y (d) el momento angular del sistema con respecto al punto\(C\).

Si un sistema plano está experimentando traslación lineal, es decir, está viajando en línea recta, ¿puede tener impulso angular?

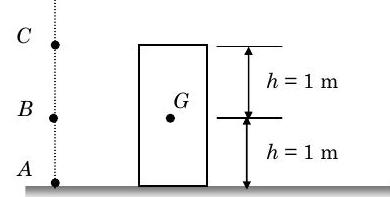
Figura\(\PageIndex{3}\): Bloque que viaja a lo largo de una superficie horizontal, con tres puntos de referencia alineados verticalmente.

Un sistema plano y rígido que gira alrededor de un eje centroidal fijo

Muchos sistemas exhiben este tipo de movimiento: la rotación de un ventilador de techo, la rotación del rotor en un motor y la rotación de un tiovivo. Un eje centroidal es un eje de rotación que cruza el centro de masa del sistema. La rotación de la escobilla y el brazo de su limpiaparabrisas en un automóvil no se ajusta a esta categoría porque no gira alrededor de un eje centroidal de la combinación limpiaparabrisas y brazo. Lo mismo sería cierto de la rotación de un péndulo simple alrededor de un punto de pivote no centroidal.

Para un sistema de plano giratorio haremos uso, sin pruebas, de una relación cinemática para la velocidad de cualquier punto en un sistema rígido que gira en el\(x \text{-} y\) plano alrededor de un eje fijo:\[\begin{array}{l} \mathbf{V} &= \vec{\omega} \times \mathbf{r} \\ &=\left(\omega_{z} \mathbf{k}\right) \times (x \mathbf{i} + y \mathbf{j}) = \left| \begin{array}{lll} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & 0 & \omega_{z} \\ x & y & 0 \end{array} \right| \\ &= -y \omega_{z} \mathbf{i} + x \omega_{z} \mathbf{j} \\[4pt] &= r \omega_{z} \left( \dfrac{-y \mathbf{i} + x \mathbf{j}}{r}\right) = \left(r \omega_{z}\right) [-(\sin \theta) \mathbf{i} + (\cos \theta) \mathbf{j}] \end{array} \nonumber \]

Tenga en cuenta que el vector de velocidad angular tiene una magnitud\(\omega_{z}\) y apunta en la dirección del\(z\) eje positivo.

Cuando piensas en usar la regla de la derecha para cruzar el vector\(\mathbf{\omega} =\omega_{z} \mathbf{k}\) con el\(\mathbf{r}\) vector, alinea tus dedos con el\(z\) eje positivo y rizarlos hacia el vector radial\(\mathbf{r}\). Ahora tu pulgar debería apuntar en una dirección normal al\(\mathbf{r}\) vector.

Cuando nos limitamos aún más a sistemas planos que giran alrededor de un eje centroidal, un eje que pasa por el centro de masa, calculamos el momento angular de la siguiente manera:

\[ \begin{array}{ll} L_{G, \text{ sys}} &= \displaystyle \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} (\mathbf{r} \times \mathbf{V}) \rho \ d V\kern-0.8em\raise0.3ex- & \left| \begin{array}{l} \text{where } \mathbf{V} = \omega_z \mathbf{k} \times \mathbf{r} \text{ since only} \\ \text{rotation about z-axis is possible} \end{array} \right. \\ &= \displaystyle \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} \left[ \mathbf{r} \times \left( \omega_z \mathbf{k} \times \mathbf{r} \right) \right] \rho \ d V\kern-0.8em\raise0.3ex- & \left| \begin{array}{l} \text{The rotational velocity } \omega_z \\ \text{is a constant.} \end{array} \right. \\ &=\omega_z \displaystyle \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} \underbrace{ \left[ \mathbf{r} \times \left( \mathbf{k} \times \mathbf{r} \right) \right] }_{= | \mathbf{r} \cdot \mathbf{r} | \mathbf{k} = r^2 \mathbf{k}} \rho \ d V\kern-0.8em\raise0.3ex- & \left| \begin{array}{l} \text{The double cross product can be} \\ \text{simplified using cylindrical coordinates} \\ \text{where } \mathbf{r} = r \ \mathbf{e}_{\mathbf{r}}, \ \mathbf{k} \times \mathbf{e}_{\mathbf{r}} = \mathbf{e}_{\theta}, \text{ and} \\ \mathbf{e}_{\mathbf{r}} \times \mathbf{e}_{\theta} = \mathbf{k}. \text{ (See Section 5.5)} \end{array} \right. \\[4pt] &= \omega_z \displaystyle \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} \left[ r^2 \mathbf{k} \right] \rho \ d V\kern-0.8em\raise0.3ex- \\ &= \omega_z \mathbf{k} \underbrace{ \left[ \displaystyle \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} r^2 \rho \ d V\kern-0.8em\raise0.3ex- \right] }_{= \text{Mass moment of inertia } I_G } & \left| \begin{array}{l} \text{The quantity in the brackets is} \\ \text{called the mass moment of inertia} \\ \text{about the } z \text{-axis that contains} \\ \text{the center of mass } G. \end{array} \right. \\ &= \omega_z I_G \mathbf{k} \end{array} \nonumber \]

Así, la magnitud del momento angular de un sistema plano rígido que gira alrededor de un eje centroidal fijo es igual al producto de la velocidad rotacional\(\omega_{z}\) alrededor del\(z\) eje -eje y el momento de inercia\(I_{G}\) de masa del sistema alrededor del\(z\) eje -eje. Como se muestra en la Figura\(\PageIndex{4}\), una masa puede tener un momento de inercia de masa alrededor de cualquier eje\(x\)\(y\), o\(z\).

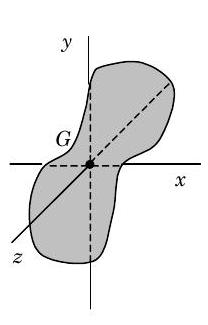
Figura\(\PageIndex{4}\): Momento de inercia de una masa.

El momento de inercia de masa alrededor del\(z\) eje se evaluaría utilizando la integral

\[ I_{G, \ z} = \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} r^2 \rho \ d V\kern-1.0em\raise0.3ex- = \begin{cases} \displaystyle \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} \left( x^2 + y^2 \right) \rho \ dx \ dy & \text{where } d V\kern-1.0em\raise0.3ex- = dx \ dy \\[4pt] \quad\quad\quad \text{or} \\[4pt] \displaystyle \int\limits_{V\kern-0.5em\raise0.3ex-_{\text{sys}}} r^2 \rho \ r \ d \theta \ dr & \text{where } d V\kern-1.0em\raise0.3ex- = r \ d \theta \ dr \end{cases} \nonumber \]

Dependiendo de la forma del objeto, la\(\mathrm{r} \text{-} \theta\) formulación\(\mathrm{x} \text{-} \mathrm{y}\) o puede ser preferible. Las dimensiones de la masa momento de inercia son\([\mathrm{M}][\mathrm{L}]^{2}\). Las unidades típicas están\(\mathrm{kg} \cdot \mathrm{m}^{2}\) en SI y\(\mathrm{lbm} \cdot \mathrm{ft}^{2}\) en USCS. Los valores para un sólido rectangular, un cilindro sólido y una esfera sólida se pueden encontrar en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Momento de inercia de masa centroidal para algunas formas comunes.

6.2.3 ¿Cómo se transporta el momento angular a través de los límites de un sistema?

El momento angular alrededor del punto\(O\) se transporta a través del límite de un sistema por dos mecanismos: el transporte de momento angular con fuerzas externas y el transporte de momento angular con flujo másico.

Transporte de momento angular con fuerzas

Cuando se aplica una fuerza externa a un sistema como se discutió anteriormente produce un momento con respecto al punto\(O\). Este momento representa una tasa de transporte de momento angular. Más específicamente, la tasa neta de transporte del momento angular alrededor del punto\(O\) en un sistema con debido a la fuerza externa se escribe matemáticamente como la suma de los momentos individuales:\[\dot{\mathbf{L}}_{O, \text { forces}} = \sum_{j} \mathbf{M}_{O, \ j} = \sum_{j}\left(\mathbf{r}_{j} \times \mathbf{F}_{j}\right) = \left[ \begin{array}{c} \text { Transport rate of } \\ \text { angular momentum } \\ \text { with external forces } \end{array} \right] \nonumber \]

El momento alrededor del punto\(O\) debido a la fuerza gravitacional distribuida o peso puede mostrarse igual al momento producido por la fuerza del peso que actúa en el centro de masa (o centro de gravedad) del sistema. Los pares de fuerza que actúan sobre el sistema producen un momento y también transportan el momento angular a través del límite del sistema. Pensando en el momento de una fuerza como una tasa de transporte de impulso lineal, las dimensiones de un momento son\([ \text{Force} ][\mathrm{L}] = \left\{ [\mathrm{M}][\mathrm{L}]^{2} / [\mathrm{T}] \right\} / [\mathrm{T}] =[\mathrm{M}] [\mathrm{L}]^{2} [\mathrm{T}]^{-2} .\)

Transporte de momento angular con flujo másico

Como se mostró anteriormente, cada bulto de masa con una velocidad tiene un momento angular alrededor de un punto\(O\). Cuando se permite que la masa fluya a través del límite de un sistema abierto, cada bulto de masa lleva consigo un impulso lineal. Por lo tanto, el momento angular de un sistema abierto también se puede cambiar mediante el flujo másico que lleva el momento angular a través del límite del sistema.

La velocidad a la que el momento angular alrededor del punto\(O\) se transporta a través del límite puede representarse por el producto del caudal másico y la velocidad local en el límite asumiendo que la velocidad es uniforme:\[\dot{\mathbf{L}}_{O, \text { mass}} = \dot{m} (\mathbf{r} \times \mathbf{V}) = \left[\begin{array}{c} \text { Transport rate of } \\ \text { angular momentum } \\ \text { with mass flow } \end{array}\right] \nonumber \] ¿dónde\(\dot{m}\) está el caudal másico en el límite de flujo,\(\mathbf{r}\) es la posición del límite de flujo con respecto al punto\(O\), y\(\mathbf{V}\) es la velocidad local del flujo. Ahora combinando esto para todos los límites de flujo, la tasa neta de transporte en el sistema de momento angular alrededor del punto se\(O\) puede obtener sumando los transportes en todos los límites de flujo:\[\mathbf{L}_{O, \text { mass, net}} = \sum_{in} \left( \mathbf{r}_{i} \times \mathbf{V}_{i}\right) \dot{m}_{i} - \sum_{out} \left(\mathbf{r}_{e} \times \mathbf{V}_{e}\right) \dot{m}_{e} \nonumber \]

6.2.4 ¿Cómo se puede generar o consumir el momento angular en un sistema?

La experiencia ha demostrado que el momento angular de un sistema no puede crearse ni destruirse; por lo tanto, se conserva el momento angular.

6.2.5 Poniéndolo todo junto

Utilizando el marco contable, podemos desarrollar la siguiente declaración para la conservación del momento angular sobre el punto\(O\):\[\left[ \begin{array}{c} \text { Rate of accumulation } \\ \text { of } \\ \text { angular momentum } \\ \text { inside a system } \\ \text { at time } t \end{array}\right] = \left[\begin{array}{c} \text { Net transport rate of } \\ \text { angular momentum } \\ \text { into the system } \\ \text { by external forces } \\ \text { at time } t \end{array}\right] + \left[ \begin{array}{c} \text { Net transport rate of } \\ \text { angular momentum } \\ \text { into the system } \\ \text { by mass flow } \\ \text { at time } t \end{array}\right] \nonumber \]

En los símbolos la velocidad-forma de la conservación del momento angular alrededor del punto\(O\) se vuelve\[\frac{d \mathbf{L}_{O, \text { sys}}}{d t} = \sum_{j} \mathbf{M}_{O, \ j} + \sum_{in} \left(\mathbf{r}_{i} \times \mathbf{V}_{i}\right) \dot{m}_{i} - \sum_{out} \left(\mathbf{r}_{e} \times \mathbf{V}_{e}\right) \dot{m}_{e} \nonumber \] De nuevo, al igual que con el momento lineal y la masa, el uso juicioso de los supuestos de modelado a menudo simplificará esta ecuación a medida que modelamos sistemas.